采用双通道卷积神经网络构建的随机脉冲噪声深度降噪模型

徐少平; 林珍玉; 崔燕; 刘蕊蕊; 杨晓辉

doi:10.11999/JEIT190796

采用双通道卷积神经网络构建的随机脉冲噪声深度降噪模型

doi: 10.11999/JEIT190796

南昌大学信息工程学院南昌 330031

基金项目: 国家自然科学基金(61662044, 61163023)，江西省自然科学基金(20171BAB202017)

详细信息

作者简介:
徐少平：男，1976年生，博士，教授，博士生导师，主要研究方向为图形图像处理技术、机器视觉、虚拟手术仿真

林珍玉：女，1996年生，硕士生，研究方向为图形图像处理技术、机器视觉

崔燕：女，1996年生，硕士生，研究方向为图形图像处理技术、机器视觉

刘蕊蕊：女，1995年生，硕士生，研究方向为图形图像处理技术、机器视觉

杨晓辉：男，1978年生，博士，副教授，主要研究方向为故障诊断及图像处理

通讯作者:
徐少平　xushaoping@ncu.edu.cn

中图分类号: TN911.73; TP391
计量
- 文章访问数: 2105
- HTML全文浏览量: 741
- PDF下载量: 71
- 被引次数: 0
出版历程
- 收稿日期: 2019-10-16
- 修回日期: 2020-07-20
- 网络出版日期: 2020-07-30
- 刊出日期: 2020-10-13

A Dual-Channel Deep Convolutional Neural Network Model for Random-Valued Impulse Noise Removal

School of Information Engineering, Nanchang University, Nanchang 330031, China

Funds: The National Natural Science Foundation of China (61662044, 61163023), The Natural Science Foundation of Jiangxi Province (20171BAB202017)

摘要

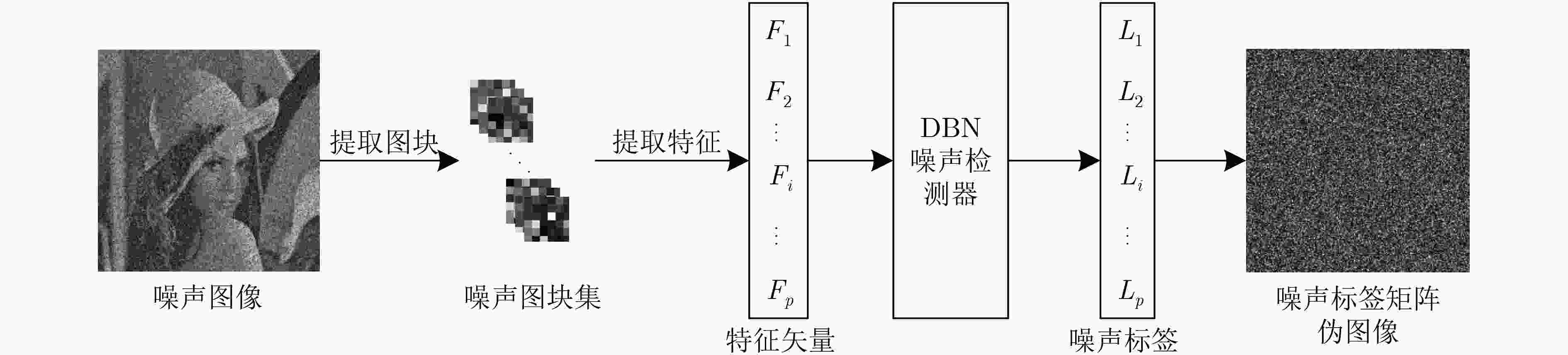
摘要: 为提高对随机脉冲噪声(RVIN)图像的降噪效果，该文提出一种被称为双通道降噪卷积神经网络(D-DnCNN)的RVIN深度降噪模型。首先，提取多个不同阶对数差值排序(ROLD)统计值及1个边缘特征统计值构成描述图块中心像素点是否为RVIN噪声的噪声感知特征矢量。其次，利用预先训练好的深度置信网络(DBN)预测模型实现特征矢量到噪声标签的映射，完成对噪声图像中噪声点的检测。再次，在噪声检测标签的指示下采用Delaunay三角剖分插值算法快速修复噪声像素点从而获得初步复原图像。最后，将初步复原图像作为参考图像与噪声图像联接(concatenate)后输入D-DnCNN模型后获得残差图像，将参考图像减去残差图像即可获得降噪后图像。实验数据表明：D-DnCNN模型在各个噪声比例下的降噪效果均显著超过了现有的经典开关型RVIN降噪算法，与普通的单通道RVIN深度降噪模型相比也有较大幅度提升。
- 图像处理 /
- 随机脉冲噪声 /
- 双通道降噪卷积神经网络 /
- 参考图像 /
- 噪声感知特征 /
- 噪声检测 /
- 插值
Abstract: A Dual-channel Denoising Convolutional Neural Network (D-DnCNN) model for the removal of Random-Valued Impulse Noise (RVIN) is proposed. To obtain the reference image quickly, several Rank-Ordered Logarithmic absolute Difference (ROLD) statistics and one edge feature statistic are first extracted from a local window to construct a RVIN-aware feature vector which can describe the central pixel of the patch is RVIN or not. Next, a noise detector based on Deep Belief Network (DBN) is trained to map the extracted feature vectors to their corresponding noise labels to detect all noise-like pixels in the observed image. Then, under the guidance of noise labels, the Delaunay triangulation-based interpolation algorithm is exploited to restore all detected noise-like pixels quickly and generate a preliminary restored image used as reference image. Finally, the reference image and the noisy image are simultaneously fed into the D-DnCNN model to output its corresponding residual image, and the final restored image can be obtained by subtracting the residual image from the noisy image. Extensive experimental results show that, the denoising effect of the proposed D-DnCNN denoising model outperforms the existing state-of-art switching ones across a range of noise ratios, and it also works better than the ordinary single-channel DnCNN model.
- Image processing /
- Random-Valued Impulse Noise(RVIN) /
- Dual-channel Denoising Convolutional Neural Network(D-DnCNN) /
- Reference image /
- Noise-aware feature /
- Noise detection /
- Interpolation

HTML全文

图 1 基于DBN的噪声标签矩阵生成流程

下载: 全尺寸图片幻灯片

图 2 利用Delaunay三角剖分插值算法对Lena噪声图像复原效果

下载: 全尺寸图片幻灯片

图 3 带辅助通道的CNN深度卷积神经网络的RVIN降噪模型框架

下载: 全尺寸图片幻灯片

图 4 各算法对Lena图像降噪的效果对比

下载: 全尺寸图片幻灯片

表 1 DBN网络在Set12测试集图像上的预测准确性

图像	20%噪声			40%噪声			60%噪声			检测正确率均值
图像	False	Miss	Accuracy	False	Miss	Accuracy	False	Miss	Accuracy	检测正确率均值
Cameraman	838	2257	0.9528	1914	3952	0.9105	3863	4062	0.8791	0.9141
House	209	1896	0.9679	911	3665	0.9302	2430	4123	0.9000	0.9327
Peppers	400	2524	0.9554	1254	4402	0.9137	3462	4489	0.8787	0.9159
Starfish	536	3217	0.9427	1594	5753	0.8879	5558	4647	0.8443	0.8916
Monarch	489	2776	0.9502	1773	4788	0.8999	4291	4313	0.8687	0.9063
Airplane	1108	2516	0.9447	1979	4514	0.9009	4286	4203	0.8705	0.9054
Parrot	588	2723	0.9495	1877	4465	0.9032	4374	4204	0.8691	0.9073
Lena	755	8303	0.9654	2342	15574	0.9317	9976	17336	0.8958	0.9310
Barbara	2219	12393	0.9443	8329	22147	0.8837	25515	18555	0.8319	0.8866
Boat	1758	10620	0.9564	5318	19001	0.9072	16137	18645	0.8673	0.9103
Man	1714	9717	0.9564	3976	17712	0.9173	13760	18459	0.8771	0.9169
Couple	2027	11049	0.9501	5553	19695	0.9037	16993	19032	0.8626	0.9055

下载: 导出CSV

表 2 不同噪声比例下各个降噪算法在BSD68测试图像集上所获得的PSNR均值 (dB)

算法	噪声比例(%)
算法	10	20	30	40	50	60
ROLD-EPR	30.24	28.26	26.97	25.96	25.04	23.98
ASWM	28.90	27.99	27.01	25.82	23.84	21.05
ROR-NLM	27.29	26.67	25.88	24.69	22.73	20.14
WCSR	30.11	27.93	26.55	25.51	24.52	23.49
ALOHA	31.75	29.04	25.13	23.74	21.81	18.79
WIN5-RB	34.67	31.46	29.02	27.11	25.46	23.68
RED-Net	33.11	30.68	28.87	27.29	25.81	24.37
LSM-NLR	28.86	26.85	25.59	24.63	23.76	22.86
S-DnCNN	35.76	32.41	30.10	27.79	26.15	24.20
本文D-DnCNN	35.71	32.72	30.56	28.62	26.76	25.31

下载: 导出CSV

表 3 D-DnCNN与S-DnCNN算法在真实噪声图像集上降噪效果PSNR对比(dB)

对比算法	图像编号										均值
对比算法	1	2	3	4	5	6	7	8	9	10	均值
S-DnCNN	46.85	43.79	52.98	49.64	47.54	43.52	52.47	43.58	42.24	40.66	46.32
本文D-DnCNN	47.45	44.56	54.20	50.32	48.27	44.10	53.81	45.26	43.17	43.17	47.43

下载: 导出CSV

表 4 各算法执行时间的比较(s)

算法	执行时间	算法	执行时间
ROLD-EPR	5.6	WIN5RB	22.8
ASWM	86.3	LSM-NLR	257.2
ROR-NLM	43.1	RED-Net	5.3
WCSR	1085.1	S-DnCNN	4.1
ALOHA	1875.2	D-DnCNN	5.3

下载: 导出CSV

参考文献(20)

马济通, 邱天爽, 李蓉, 等. 脉冲噪声下基于Renyi熵的分数低阶双模盲均衡算法[J]. 电子与信息学报, 2018, 40(2): 378–385. doi: 10.11999/JEIT170366

MA Jitong, QIU Tianshuang, LI Rong, et al. Dual-mode blind equalization algorithm based on Renyi entropy and fractional lower order statistics under impulsive noise[J]. Journal of Electronics &Information Technology, 2018, 40(2): 378–385. doi: 10.11999/JEIT170366

徐少平, 张贵珍, 李崇禧, 等. 基于深度置信网络的随机脉冲噪声快速检测算法[J]. 电子与信息学报, 2019, 41(5): 1130–1136. doi: 10.11999/JEIT180558

XU Shaoping, ZHANG Guizhen, LI Chongxi, et al. A fast random-valued impulse noise detection algorithm based on deep belief network[J]. Journal of Electronics &Information Technology, 2019, 41(5): 1130–1136. doi: 10.11999/JEIT180558

GARNETT R, HUEGERICH T, CHUI C, et al. A universal noise removal algorithm with an impulse detector[J]. IEEE Transactions on Image Processing, 2005, 14(11): 1747–1754. doi: 10.1109/TIP.2005.857261

DONG Yiqiu, CHAN R H, and XU Shufang. A detection statistic for random-valued impulse noise[J]. IEEE Transactions on Image Processing, 2007, 16(4): 1112–1120. doi: 10.1109/TIP.2006.891348

ROY A, SINGHA J, DEVI S S, et al. Impulse noise removal using SVM classification based fuzzy filter from gray scale images[J]. Signal Processing, 2016, 128: 262–273. doi: 10.1016/j.sigpro.2016.04.007

SOLEIMANY S and HAMGHALAM M. A novel random-valued impulse noise detector based on MLP neural network classifier[C]. 2017 Artificial Intelligence and Robotics, Qazvin, Iran, 2017: 165–169. doi: 10.1109/RIOS.2017.7956461.

ZHANG Kai, ZUO Wangmeng, CHEN Yunjin, et al. Beyond a Gaussian denoiser: Residual learning of deep CNN for image denoising[J]. IEEE Transactions on Image Processing, 2017, 26(7): 3142–3155. doi: 10.1109/TIP.2017.2662206

ZHANG Kai, ZUO Wangmeng, and ZHANG Lei. FFDNet: Toward a fast and flexible solution for CNN-based image denoising[J]. IEEE Transactions on Image Processing, 2018, 27(9): 4608–4622. doi: 10.1109/TIP.2018.2839891

GUO Shi, YAN Zifei, ZHANG Kai, et al. Toward convolutional blind denoising of real photographs[C]. 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, USA, 2019: 1712–1722. doi: 10.1109/CVPR.2019.00181.

YU Hancheng, ZHAO Li, and WANG Haixian. An efficient procedure for removing random-valued impulse noise in images[J]. IEEE Signal Processing Letters, 2008, 15: 922–925. doi: 10.1109/LSP.2008.2005051

SUN Jiande, LIU Xiaocui, WAN Wenbo, et al. Video hashing based on appearance and attention features fusion via DBN[J]. Neurocomputing, 2016, 213: 84–94. doi: 10.1016/j.neucom.2016.05.098

AKKOUL S, LEDEE R, LECONGE R, et al. A new adaptive switching median filter[J]. IEEE Signal Processing Letters, 2010, 17(6): 587–590. doi: 10.1109/LSP.2010.2048646

XIONG Bo and YIN Zhouping. A universal denoising framework with a new impulse detector and nonlocal means[J]. IEEE Transactions on Image Processing, 2012, 21(4): 1663–1675. doi: 10.1109/TIP.2011.2172804

CHEN C L P, LIU Licheng, CHEN Long, et al. Weighted couple sparse representation with classified regularization for impulse noise removal[J]. IEEE Transactions on Image Processing, 2015, 24(11): 4014–4026. doi: 10.1109/TIP.2015.2456432

JIN K H and YE J C. Sparse and low-rank decomposition of a Hankel structured matrix for impulse noise removal[J]. IEEE Transactions on Image Processing, 2018, 27(3): 1448–1461. doi: 10.1109/TIP.2017.2771471

LIU Peng and FANG Ruogu. Learning pixel-distribution prior with wider convolution for image denoising[EB/OL]. https://arxiv.org/abs/1707.09135, 2017.

MAO Xiaojiao, SHEN Chunhua, and YANG Yubin. Image restoration using very deep convolutional encoder-decoder networks with symmetric skip connections[C]. The 30th International Conference on Neural Information Processing Systems, Barcelona, Spain, 2016: 2810–2818.

HUANG Tao, DONG Weisheng, XIE Xuemei, et al. Mixed noise removal via Laplacian scale mixture modeling and nonlocal low-rank approximation[J]. IEEE Transactions on Image Processing, 2017, 26(7): 3171–3186. doi: 10.1109/TIP.2017.2676466

ARBELÁEZ P, MAIRE M, FOWLKES C, et al. Contour detection and hierarchical image segmentation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2011, 33(5): 898–916. doi: 10.1109/TPAMI.2010.161

YUE Zongsheng, YONG Hongwei, ZHAO Qian, et al. Variational denoising network: Toward blind noise modeling and removal[EB/OL]. https://arxiv.org/abs/1908.11314v1, 2019.

施引文献

资源附件(0)

访问统计