Adaptive ASR Filtering in Impulsive Noise Environments
-
摘要: 在基于alpha稳定分布模型的脉冲噪声处理领域中,经典滤波方法多采用Cauchy分布和Meridian分布等alpha稳定分布特例,其脉冲抑制能力有限。对此,该文基于M估计理论和
$ {\rm{AS}}\alpha {\rm{S}} $ 分布模型,构造稳健滤波代价函数簇,提出ASR稳健滤波方法,利用影响函数分析其稳健性,构建稳健滤波的统一理论基础,将Myriad滤波,Meridian滤波统一起来。给出线性度参数表达式,并采用阈值选择法实现自适应选择。此外,提出AS-FT滤波方法,以线性调频(LFM)信号在脉冲噪声下的参数估计为例,表明ASR滤波方法的稳健性。仿真实验表明,ASR稳健滤波方法,与中值滤波、Myriad滤波、分数低阶等传统的稳健滤波方法相比,具有良好的鲁棒性。Abstract: In the field of impulsive noise processing based on alpha-stable distribution model, the classical filtering methods have been largely motivated by special cases of alpha-stable family such as Cauchy distribution and Meridian distribution, and their pulse suppression ability is limited. To address the above limitations, a class of robust cost functions are devised and a robust filtering method ASR (${\rm{AS}}\alpha {\rm{S}} $ kobust) is proposed, based on the M estimation theory and the$ {\rm{AS}}\alpha {\rm{S}} $ distribution model, with its robustness analyzed by the influence functions. Then the expression of the linearity parameter is proposed and a threshold selection method is adopted for an adaptive linearity parameter selection. The unified theoretical framework of robust filtering is devised, and Myriad filters and Meridian filters are interpreted within the unifying framework. In addition, a filtering method which is, namely AS-FT (ASR STFT) is developed and the parameters estimation of noisy Linear Frequency Modulation (LFM) signals shows the robustness of ASR filtering. Simulation results show that the ASR method is more robust to outliers than Myriad filters, Median filters, fractional lower-order statistics and other traditional robust filters.-
Key words:
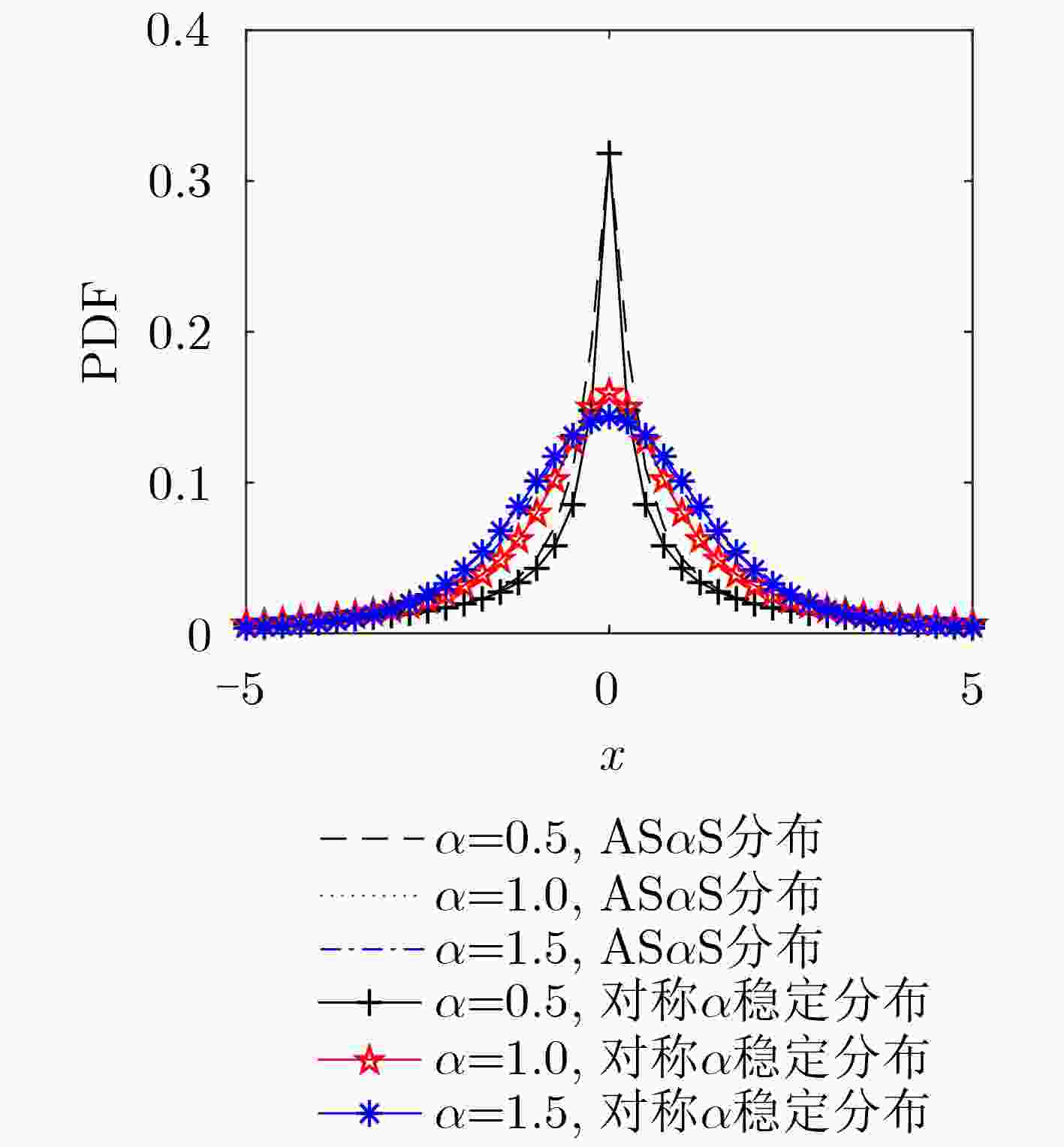
- ASαS distribution /
- Cost function /
- Influence function /
- Robust filtering
-
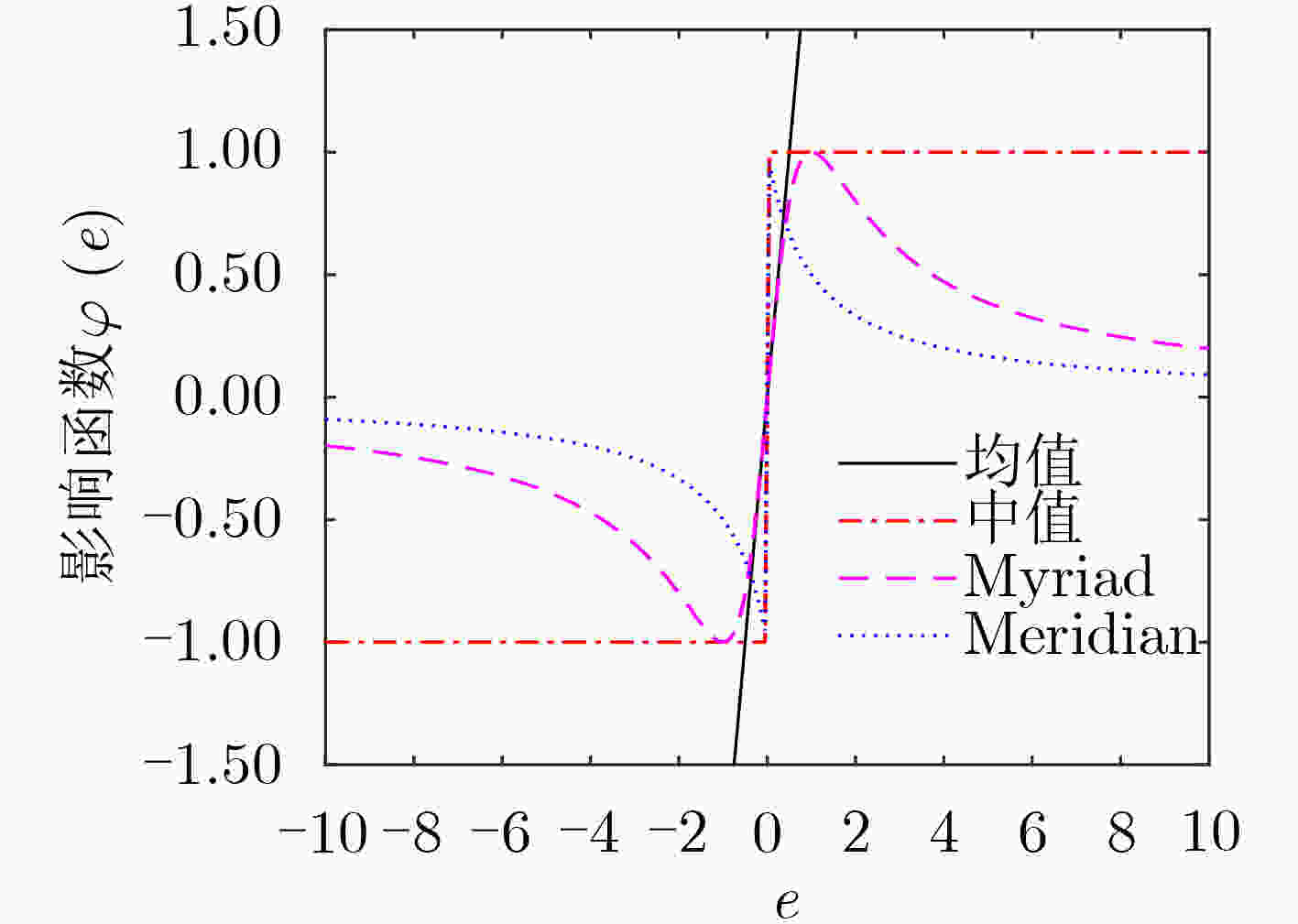
表 1 常用滤波器的代价函数与影响函数
均值滤波 中值滤波 Myriad滤波 Meridian滤波 PDF $p(x)$ ${{\exp ( - {x^2})} / {\sqrt {2\pi } }}$ ${ {\exp ( - \left| x \right|)} / {2\pi } }$ ${\gamma / {[\pi ({\gamma ^2} + {x^2})]}}$ ${{\delta / {2(\delta + \left| x \right|}}^2})$ 代价函数 $F(e)$ ${e^2}$ $\left| e \right|$ $\log ({e^2} + {\gamma ^2})$ $\log \{ \delta + \left| e \right|\} $ 影响函数 $\varphi (e)$ $2e$ ${\rm{sgn}} (e)$ $2e/({\gamma ^2} + {e^2})$ ${\rm{sgn}} (e)/(\delta + |e|)$ -
TALEBI S P and MANDIC D P. Distributed particle filtering of α-stable signals[J]. IEEE Signal Processing Letters, 2017, 24(12): 1862–1866. doi: 10.1109/LSP.2017.2761182 ZHANG Jinfen, QIU Tianshuang, WANG Peng, et al. A novel cauchy score function based DOA estimation method under alpha-stable noise environments[J]. Signal Processing, 2017, 138: 98–105. doi: 10.1016/j.sigpro.2017.03.014 杨帆, 贾辉, 刘宝树, 等. α稳定脉冲噪声下宽带电力线通信系统性能分析[J]. 电子与信息学报, 2019, 41(6): 1374–1380. doi: 10.11999/JEIT180261YANG Fan, JIA Hui, LIU Baoshu, et al. Performance analysis of broadband power-line communications systems under the alpha-stable impulsive noise[J]. Journal of Electronics &Information Technology, 2019, 41(6): 1374–1380. doi: 10.11999/JEIT180261 RAMIREZ J M and PAREDES J L. Recursive weighted myriad based filters and their optimizations[J]. IEEE Transactions on Signal Processing, 2016, 64(15): 4027–4039. doi: 10.1109/TSP.2016.2557304 ZORLU H. Optimization of weighted myriad filters with differential evolution algorithm[J]. AEU-International Journal of Electronics and Communications, 2017, 77: 1–9. doi: 10.1016/j.aeue.2017.04.020 KURKIN D, ROENKO A, LUKIN V, et al. An adaptive meridian estimator[C]. 2011 Microwaves, Radar and Remote Sensing Symposium, Kiev, Ukraine, 2011: 301–304. doi: 10.1109/MRRS.2011.6053660. 金艳, 胡碧昕, 姬红兵. α稳定分布噪声下一种稳健加权滤波的统一框架[J]. 系统工程与电子技术, 2016, 38(10): 2221–2227. doi: 10.3969/j.issn.1001-506X.2016.10.01JIN Yan, HU Bixin, and JI Hongbing. Unified framework of robust weighted filtering in α stable noise[J]. Systems Engineering and Electronics, 2016, 38(10): 2221–2227. doi: 10.3969/j.issn.1001-506X.2016.10.01 金艳, 段鹏婷, 姬红兵. 复杂噪声环境下基于LVD的LFM信号参数估计[J]. 电子与信息学报, 2014, 36(5): 1106–1112. doi: 10.3724/SP.J.1146.2013.01013JIN Yan, DUAN Pengting, and JI Hongbing. Parameter estimation of LFM signals based on LVD in complicated noise environments[J]. Journal of Electronics &Information Technology, 2014, 36(5): 1106–1112. doi: 10.3724/SP.J.1146.2013.01013 张贤达. 现代信号处理[M]. 北京: 清华大学出版社, 1995.ZHANG Xianda. Modern Signal Processing[M]. Beijing: Tsinghua University Press, 1995. 王志洋. Chirp信号参数估计方法的研究[D]. [硕士论文], 吉林大学, 2013.WANG Zhiyang. Study on parameter estimation of chirp signal[D]. [Master dissertation], Jilin University, 2013. RUPPERT D. Robust statistics: The approach based on influence functions[J]. Technometrics, 1987, 29(2): 240–241. doi: 10.1080/00401706.1987.10488218 AYSAL T C and BARNER K E. Meridian filtering for robust signal processing[J]. IEEE Transactions on Signal Processing, 2007, 55(8): 3949–3962. doi: 10.1109/tsp.2007.894383 CHEN Yunfei and CHEN Jiming. Novel SαS PDF approximations and their applications in wireless signal detection[J]. IEEE Transactions on Wireless Communications, 2015, 14(2): 1080–1091. doi: 10.1109/TWC.2014.2364181 KALLURI S and ARCE G R. Adaptive weighted myriad filter algorithms for robust signal processing in α-stable noise environments[J]. IEEE Transactions on Signal Processing, 1998, 46(2): 322–334. doi: 10.1109/78.655418 GONZALEZ J G and ARCE G R. Optimality of the myriad filter in practical impulsive-noise environments[J]. IEEE Transactions on Signal Processing, 2001, 49(2): 438–441. doi: 10.1109/78.902126 SUORANTA R. Amplitude domain approach to digital filtering: Therory and applications of L-filters[D]. [Ph.D. dissertation], Technical Research Center of Finland, 1995: 199. DJUROVIĆ I, LUKIN V V, and ROENKO A A. Removal of α-stable noise in frequency modulated signals using robust DFT forms[J]. Telecommunications and Radio Engineering, 2004, 61(7/12): 574–590. doi: 10.1615/TelecomRadEng.v61.i7.20 -








 下载:
下载:







 下载:
下载:
