A Three-dimensional Source Location Algorithm Based on Sparse Planar Array with Low Complexity
-
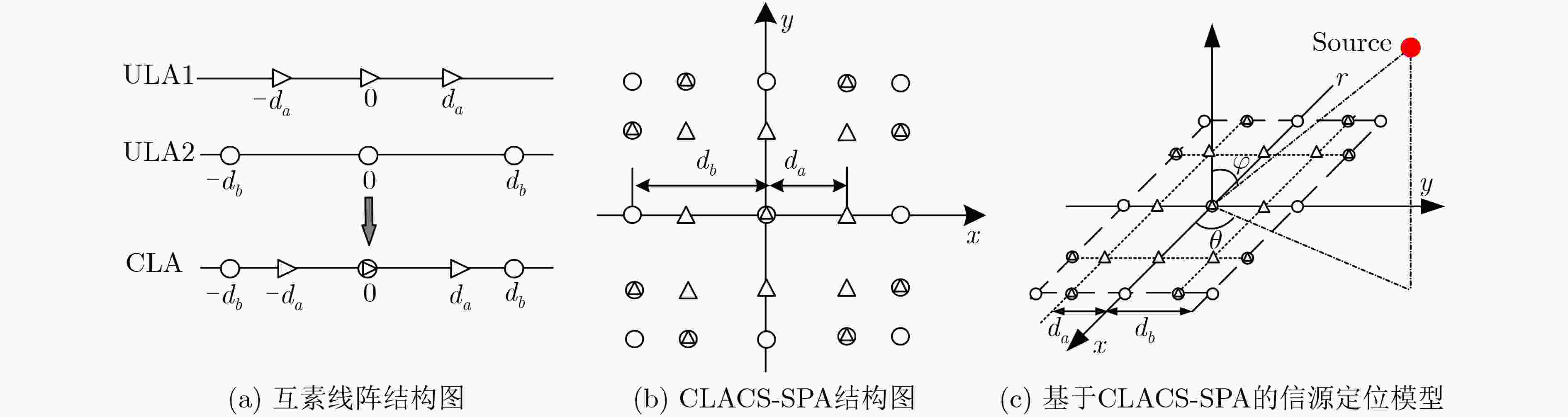
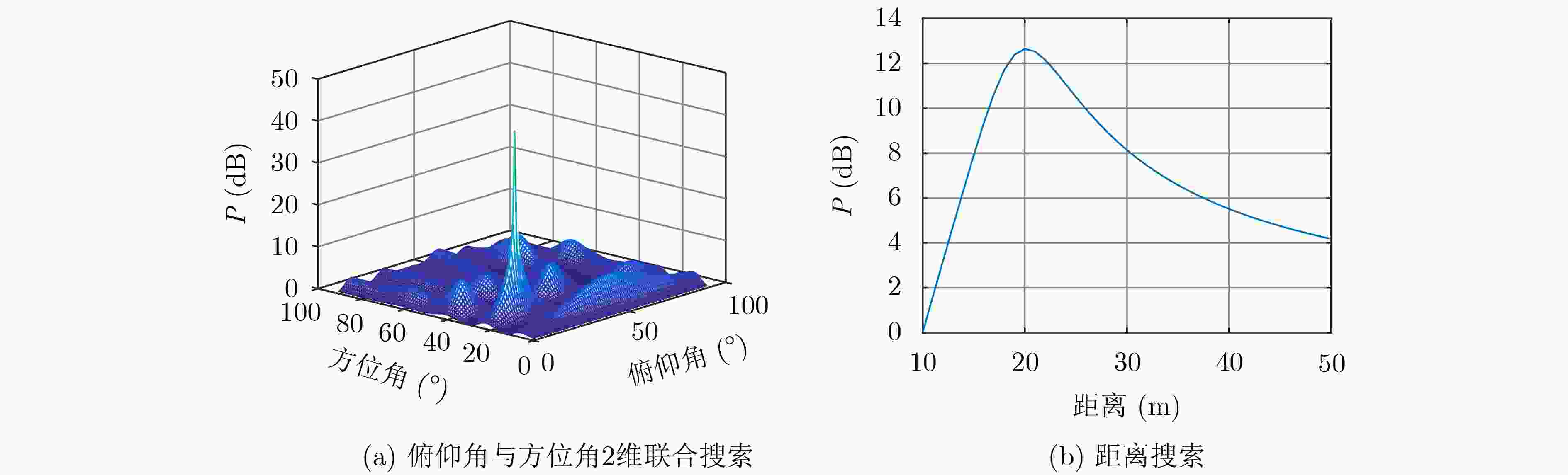
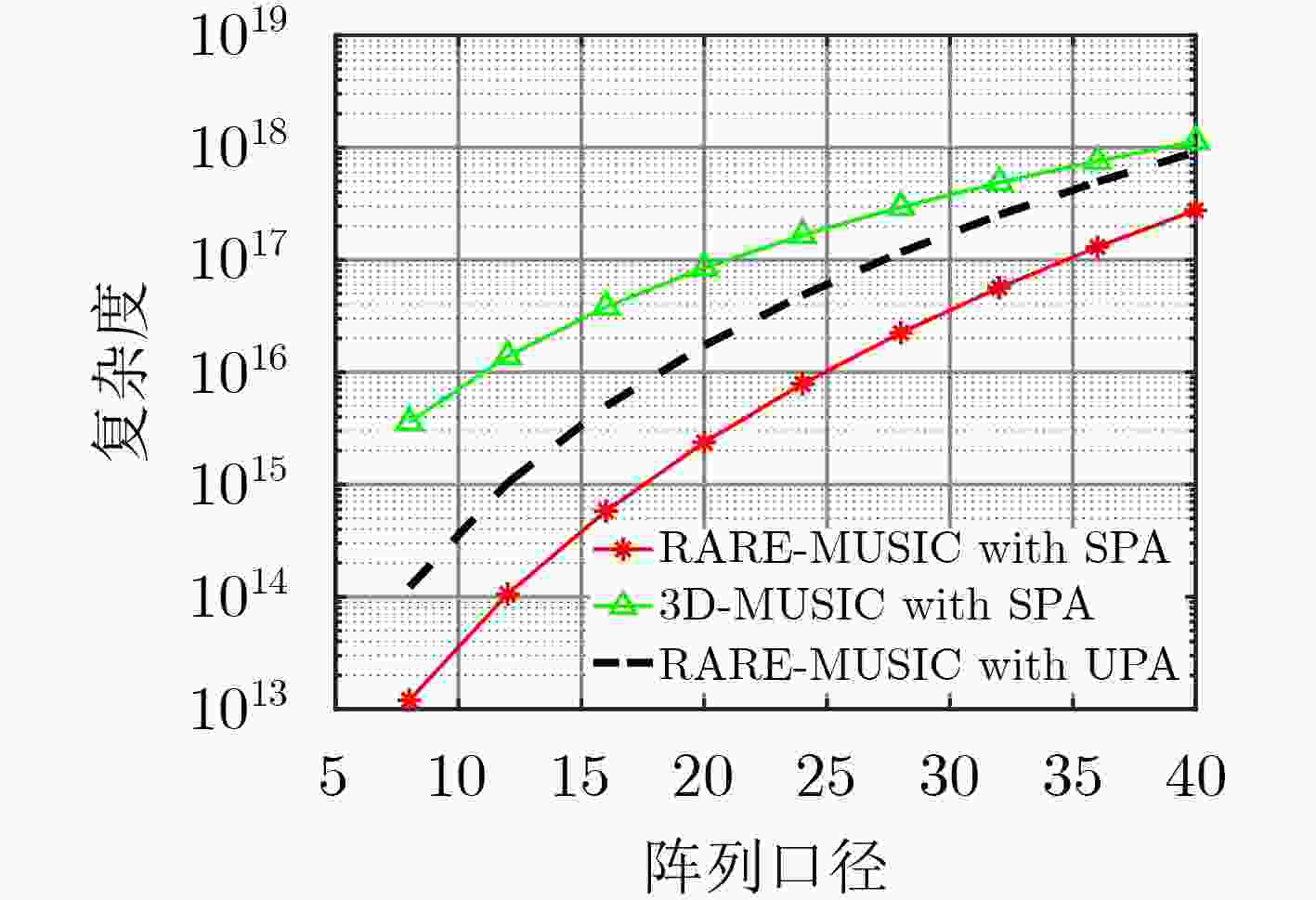
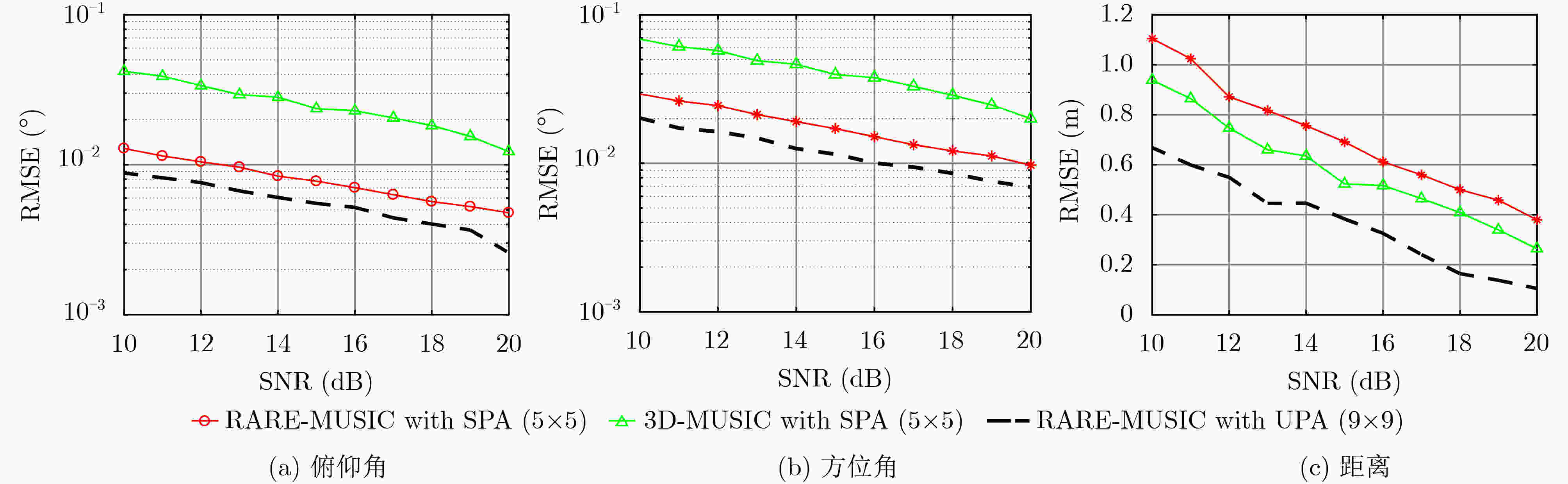
摘要: 针对3维信源定位中阵列结构过于复杂、算法复杂度过高、谱峰搜索范围过大的问题,该文提出一种基于互素线阵互素平移的稀疏面阵(CLACS-SPA)的3维降秩MUSIC算法(RARE-MUSIC)。所提CLACS-SPA拥有中心对称的互素稀疏面阵结构,相较于同口径均匀面阵结构减少了大量的阵元,降低了阵列的结构复杂度;以CLACS-SPA为基础的3维RARE-MUSIC算法利用泰勒公式将接收信号中的方向信息与距离信息进行分离估计,从而将3维谱峰搜索转化为方位角俯仰角的2维搜索和距离项的1维搜索,降低了定位算法的计算复杂度。仿真分析表明:在口径与定位算法相同条件下,与均匀面阵结构相比,所提结构的计算复杂度降低了1~2个数量级;在相同口径与CLACS-SPA结构下,与经典3维MUSIC算法相比,所提算法的复杂度降低了2~3个数量级;在相同口径和阵元数量条件下,与经典3维MUSIC算法相比,所提算法不仅降低了计算复杂度,而且提升了方位角与俯仰角的测量精度。Abstract: A RAnk REduced MUSIC (RARE-MUSIC) algorithm based on Coprime Linear Array Coprime Shift Spare Planar Array (CLACS-SPA) is proposed, in order to solve the problems in the three-dimension source location, such as too complex array structure, too high-complexity algorithm and large partial spectrum range. The proposed CLACS-SPA has a centrosymmetric coprime sparse array structure, which reduces the number of antennas and structural complexity of the array, compared with the uniform planar array structure of the same caliber. The direction and distance information in the received signal are separated and estimated by Taylor formula, thus the three-dimensional spectral peak search is transformed into the two-dimensional search of the azimuth angle as well as elevation angle and the one-dimensional search of the distance, which reduces the computational complexity of the positioning algorithm. Simulation results show that the complexity of the proposed structure is one to two orders of magnitude lower than that of the uniform planar array structure, under the same aperture and location algorithm. In addition, for the same caliber of the proposed CLACS-SPA structure, the proposed RARE-MUSIC algorithm is less complex than the classical three-dimension MUSIC with two to three orders of magnitude. And under the same aperture and number of antennas, the proposed RARE-MUSIC greatly reduces the computational complexity and improves the measurement accuracy of azimuth and elevation angles, in comparison with the classical three-dimension MUSIC algorithm.
-
表 1 相同口径下,CLACS-SPA和UPA的阵元数量
UPA CLACS-SPA ${d_a} = a\lambda $ $a = 1$ $a = 3$ $a = 5$ $a = 11$ ${d_b} = b\lambda $ $b = 1$ $b = 4$ $b = 6$ $b = 12$ 阵元数量 625 169 81 25 -
[1] GUZEY N, XU Hao, and JAGANNATHAN S. Localization of near-field sources in spatially colored noise[J]. IEEE Transactions on Instrumentation and Measurement, 2015, 64(8): 2302–2311. doi: 10.1109/TIM.2015.2390813 [2] LIANG Junli and LIU Ding. Passive Localization of mixed near-field and far-field sources using two-stage MUSIC algorithm[J]. IEEE Transactions on Signal Processing, 2010, 58(1): 108–120. doi: 10.1109/TSP.2009.2029723 [3] TICHAVSKY D, WONG T K, and ZOLTOWSKI M D. Near-field/far-field azimuth and elevation angle estimation using a single vector hydrophone[J]. IEEE Transactions on Signal Processing, 2001, 49(11): 2498–2510. doi: 10.1109/78.960397 [4] JI Yilin, FAN Wei, and PEDERSEN G F. Near-field signal model for large-scale uniform circular array and its experimental validation[J]. IEEE Antennas and Wireless Propagation Letters, 2017, 16: 1237–1240. doi: 10.1109/LAWP.2016.2629189 [5] LIANG Junli and LIU Ding. Passive localization of near-field sources using cumulant[J]. IEEE Sensors Journal, 2009, 9(8): 953–960. doi: 10.1109/JSEN.2009.2025580 [6] JUNG T J and LEE K. Closed-Form algorithm for 3-D single-source localization with uniform circular array[J]. IEEE Antennas and Wireless Propagation Letters, 2014, 13: 1096–1099. doi: 10.1109/LAWP.2014.2327992 [7] SCHMIDT R. Multiple emitter location and signal parameter estimation[J]. IEEE Transactions on Antennas and Propagation, 1986, 34(3): 276–280. doi: 10.1109/TAP.1986.1143830 [8] ROY R and KAILATH T. ESPRIT-estimation of signal parameters via rotational invariance techniques[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1989, 37(7): 984–995. doi: 10.1109/29.32276 [9] WEN Fei, WAN Qun, FAN Rong, et al. Improved MUSIC algorithm for multiple noncoherent subarrays[J]. IEEE Signal Processing Letters, 2014, 21(5): 527–530. doi: 10.1109/LSP.2014.2308271 [10] ZHANG Dong, ZHANG Yongshun, ZHENG Guimei, et al. Two-dimensional direction of arrival estimation for coprime planar arrays via polynomial root finding technique[J]. IEEE Access, 2018, 6: 19540–19549. doi: 10.1109/ACCESS.2018.2821919 [11] ZHAO Hongwei, CAI Muren, and LIU Heng. Two-dimensional DOA estimation with reduced-dimension MUSIC algorithm[C]. International Applied Computational Electromagnetics Society Symposium (ACES), Suzhou, China, 2017: 1–2. [12] 李建峰, 沈明威, 蒋德富. 互质阵中基于降维求根的波达角估计算法[J]. 电子与信息学报, 2018, 40(8): 1853–1859. doi: 10.11999/JEIT171087LI Jianfeng, SHEN Mingwei, and JIANG Defu. Reduced-dimensional root finding based direction of arrival estimation for coprime array[J]. Journal of Electronics &Information Technology, 2018, 40(8): 1853–1859. doi: 10.11999/JEIT171087 [13] XIE Jian, TAO Haihong, RAO Xuan, et al. Passive localization of noncircular sources in the near-field[C]. International Radar Symposium (IRS), Dresden, Germany, 2015: 493–498. doi: 10.1109/IRS.2015.7226309. [14] ZHENG Wang, ZHANG Xiaofei, and ZHAI Hui. Generalized coprime planar array geometry for 2-D DOA estimation[J]. IEEE Communications Letters, 2017, 21(5): 1075–1078. doi: 10.1109/LCOMM.2017.2664809 [15] ASCHER A, LECHNER J, NOSOVIC S, et al. 3D localization of passive UHF RFID transponders using direction of arrival and distance estimation techniques[C]. The 2nd IEEE Advanced Information Technology, Electronic and Automation Control Conference (IAEAC), Chongqing, China, 2017: 1373–1379. doi: 10.1109/IAEAC.2017.8054239. [16] 李建峰, 蒋德富, 沈明威. 基于平行嵌套阵互协方差的二维波达角联合估计算法[J]. 电子与信息学报, 2017, 39(3): 670–676. doi: 10.11999/JEIT160488LI Jianfeng, JIANG Defu, and SHEN Mingwei. Joint two-dimensional direction of arrival estimation based on cross covariance matrix of parallel nested array[J]. Journal of Electronics &Information Technology, 2017, 39(3): 670–676. doi: 10.11999/JEIT160488 -





 下载:
下载:


 下载:
下载:
