Research on Mesh Generation Optimization of Finite Element Model of Human Body Based on Energy Error
-
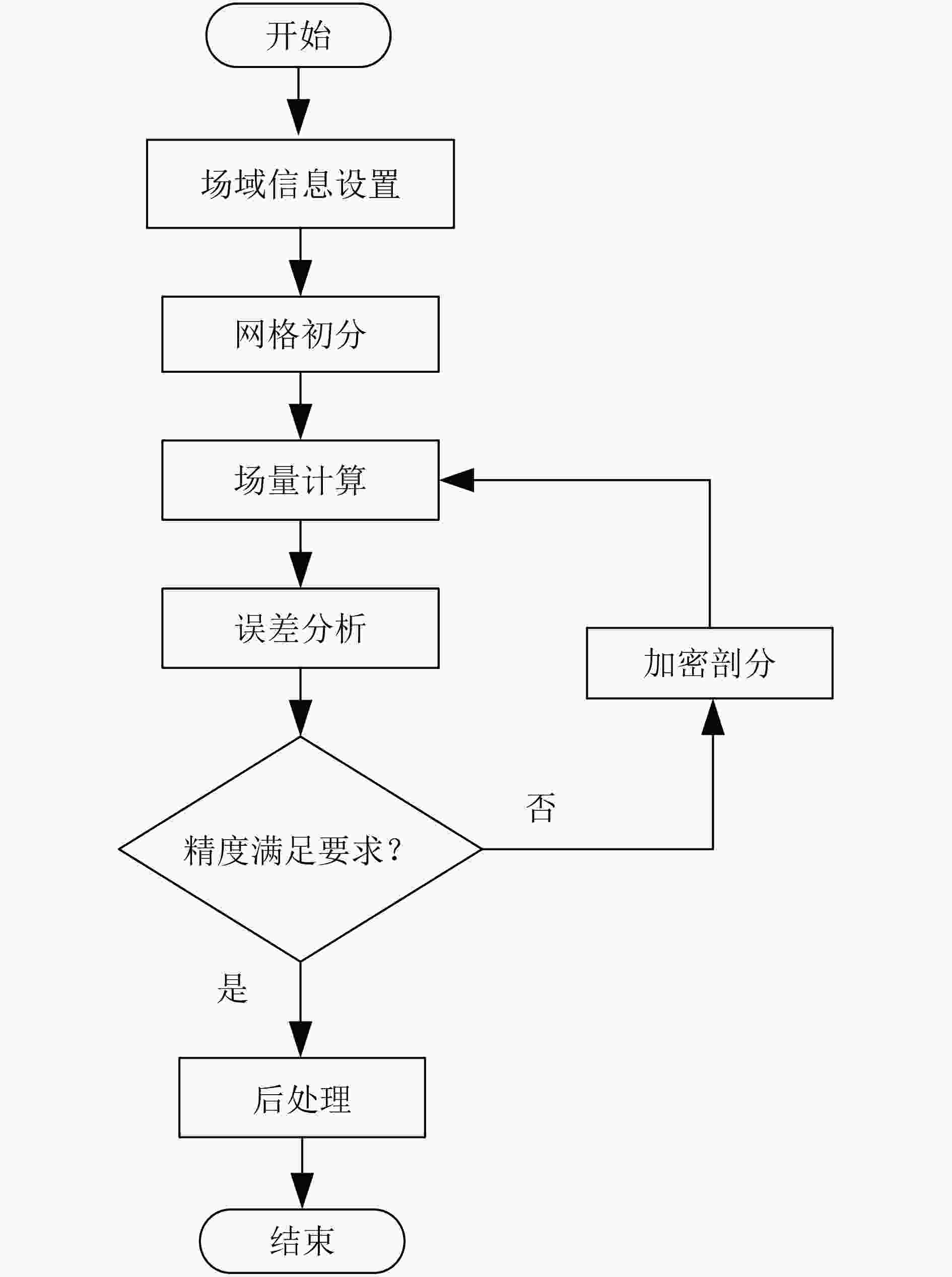
摘要: 网格剖分是有限元建模分析过程中最重要,也是工作量最大的环节,直接影响有限元分析的精度和时间。该文在研究网格自适应剖分及有限元离散误差的基础上,在高压输电场环境中建立不同复杂度的3维人体模型。通过对人体模型自适应网格剖分和手动网格剖分电场仿真结果的对比,分析能量误差变化的趋势,从而指导人体模型的建立及最佳剖分尺寸的设置。该文的研究成果,对其它有限元剖分方案的优化研究具有一定参考意义。Abstract: Meshing is the most important part of the finite element modeling and analysis process, and it also has the largest workload, which directly affects the accuracy and time of the finite element analysis. Based on the research of adaptive meshing and finite element discrete errors, three-dimensional human body models of different complexity are established in the environment of high-voltage power transmission fields. By comparing the results of the electric field simulation between the adaptive meshing of the human body model and the manual meshing, the trend of energy error changes is analyzed, so as to guide the establishment of the human body model and the setting of the optimal mesh size.The research results have certain reference significance to the optimization research of other finite element splitting schemes.
-
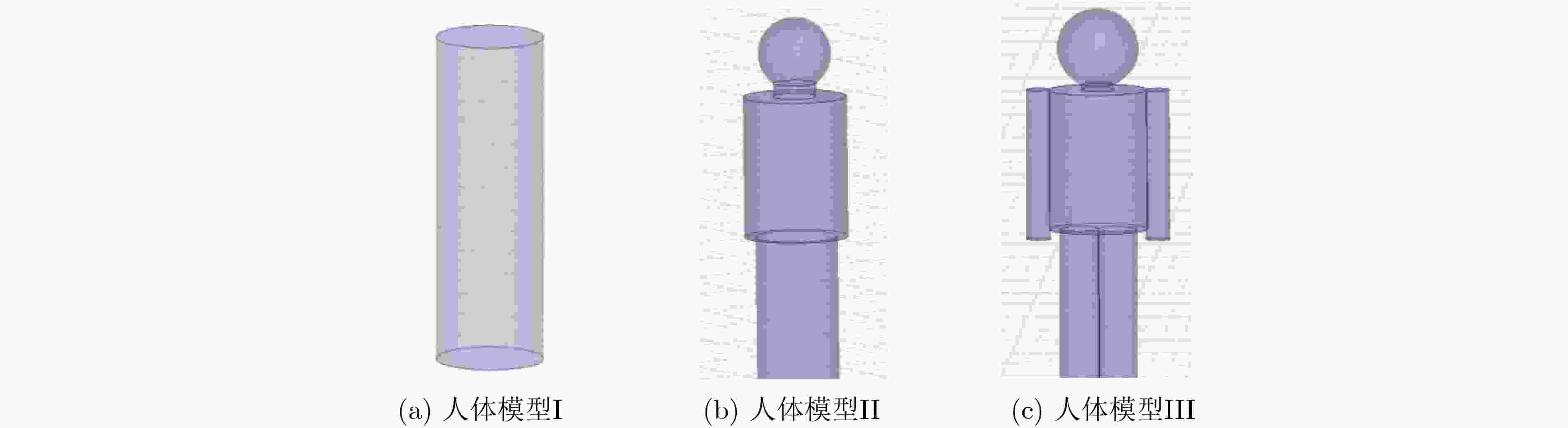
表 1 人体模型尺寸(m)
人体模型I 人体模型II 人体模型III 脚 身体 脖子 头 脚 身体 手臂 脖子 头 半径 0.28 0.19 0.24 0.10 0.17 0.05 0.12 0.03 0.04 0.20 高度 1.71 0.70 0.65 0.08 无 0.80 0.70 0.75 0.08 无 表 2 不同人体模型的方差和自适应网格剖分能量误差
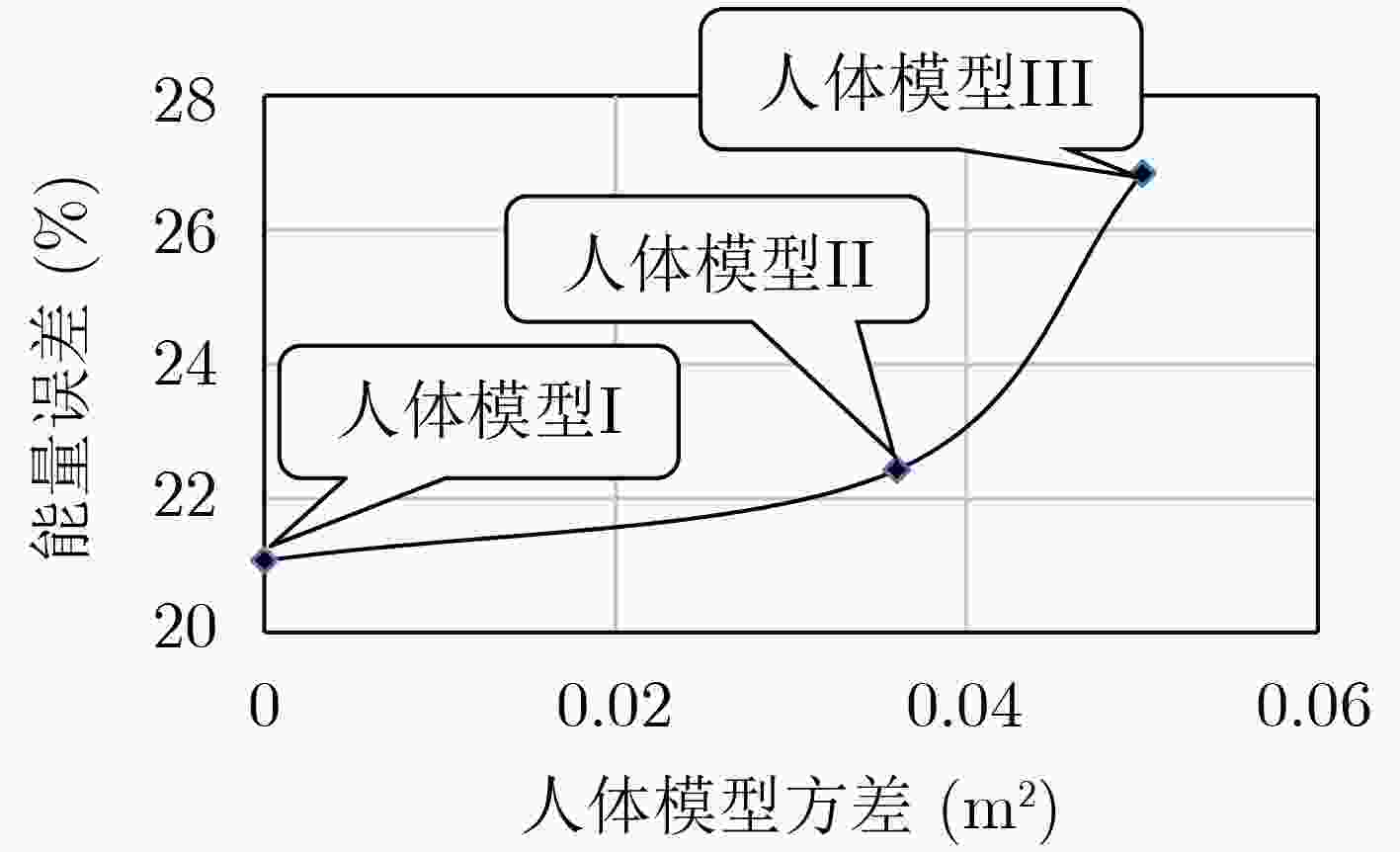
人体模型类型 人体模型I 人体模型II 人体模型III 能量误差(%) 21.0735 22.4244 26.8348 方差(m2) 0 0.036 0.050 表 3 网格尺寸0.2 m和0.5 m的模型网格数变化
人体模型I 人体模型II 人体模型III 全局网格数 网格尺寸0.2 m 281086 282154 285858 网格尺寸0.5 m 277204 280179 283806 网格数差 全局网格数差 3882 1975 2052 人体网格数 网格尺寸0.2 m 2646 2769 4987 网格尺寸0.5 m 566 1579 3615 网格数差 人体网格数差 2080 1190 1372 -
沈丹丹, 胡万晓, 苟进胜. 木托盘有限元分析精度的影响因素[J]. 包装工程, 2018, 39(17): 12–18. doi: 10.19554/j.cnki.1001-3563.2018.17.003SHEN Dandan, HU Wanxiao, and GOU Jinsheng. Factors affecting the precision of finite element analysis of wooden pallet[J]. Packaging Engineering, 2018, 39(17): 12–18. doi: 10.19554/j.cnki.1001-3563.2018.17.003 叶志红, 周海京, 刘强. 屏蔽腔内任意高度线缆端接TVS管电路的电磁耦合时域分析[J]. 电子与信息学报, 2018, 40(4): 1007–1011. doi: 10.11999/JEIT170615YE Zhihong, ZHOU Haijing, and LIU Qiang. Time domain coupling analysis for the arbitrary height cable terminated with TVS circuit in shield cavity[J]. Journal of Electronics &Information Technology, 2018, 40(4): 1007–1011. doi: 10.11999/JEIT170615 JIN Gefei, WEI Hai, CHEN Danlei, et al. Finite element meshing of complex tailings dam based on Hypermesh software[J]. China Water Transport (The Second Half) , 2019, 19(8): 96–97. 王世杰, 常延贞. 一类抛物最优控制问题的有限元误差估计[J]. 北京化工大学学报: 自然科学版, 2018, 45(6): 106–110. doi: 10.13543/j.bhxbzr.2018.06.017WANG Shijie and CHANG Yanzhen. Error estimates of the finite element method for a class of parabolic optimal control problems[J]. Journal of Beijing University of Chemical Technology:Natural Science Edition, 2018, 45(6): 106–110. doi: 10.13543/j.bhxbzr.2018.06.017 TURCKE D J and MCNEICE G M. Guidelines for selecting finite element grids based on an optimization study[J]. Computers & Structures, 1974, 4(3): 499–519. BABUŠKA I and RHEINBOLDT W C. A-Posteriori error estimates for the finite element method[J]. International Journal for Numerical Methods in Engineering, 1978, 12(10): 1597–1615. doi: 10.1002/nme.1620121010 ZIENKIEWICZ O C and ZHU J Z. The superconvergent patch recovery and a posteriori error estimates. Part 1: The recovery technique[J]. International Journal for Numerical Methods in Engineering, 1992, 33(7): 1331–1364. doi: 10.1002/nme.1620330702 AINSWORTH M, ZHU J Z, CRAIG A W, et al. Analysis of the Zienkiewicz-Zhu a-posteriori error estimator in the finite element method[J]. International Journal for Numerical Methods in Engineering, 1989, 28(9): 2161–2174. doi: 10.1002/nme.1620280912 FENG Kang. Finite element method[J]. Mathematics in Practice and Theory, 1974(4): 54–61. LI Xiangrong, ZHANG Weiwei, and NIE Yufeng. Superconvergence analysis of adaptive finite element method based on the bubble-type mesh generation[J]. Applied Mathematics Letters, 2019, 98: 322–328. doi: 10.1016/j.aml.2019.06.034 朱月风, 张洪亮, 张乘源, 等. 简化扩展有限元法精度的验证及在DCT试验中的应用[J]. 武汉大学学报: 工学版, 2019, 52(3): 216–222. doi: 10.14188/j.1671-8844.2019-03-005ZHU Yuefeng, ZHANG Hongliang, ZHANG Chengyuan, et al. Accuracy verification of simplified XFEM and its application to DCT test[J]. Engineering Journal of Wuhan University, 2019, 52(3): 216–222. doi: 10.14188/j.1671-8844.2019-03-005 苏志敏, 闫毅志, 董卫, 等. 特高拱坝有限元网格尺寸与离散误差分析[C]. 第九届南方计算力学学术交流会, 合肥, 2013: 246–250. doi: 10.19636/j.cnki.cjsm42-1250/o3.2014.s1.042.SU Zhimin, YAN Yizhi, DONG Wei, et al. Analysis on finite element mesh size and discretization error for super-high arch dam[C]. The 9th South Computational Mechanics Academic Exchange Conference, Hefei, China, 2013: 246–250. doi: 10.19636/j.cnki.cjsm42-1250/o3.2014.s1.042. 刘建涛, 杜平安, 黄明镜, 等. 曲面薄壳有限元离散误差分析和修正方法研究[J]. 系统仿真学报, 2010, 22(10): 2281–2286. doi: 10.16182/j.cnki.joss.2010.10.006LIU Jiantao, DU Ping’an, HUANG Mingjing, et al. Discrete error analysis and correction method of finite element for curved thin-walled structures[J]. Journal of System Simulation, 2010, 22(10): 2281–2286. doi: 10.16182/j.cnki.joss.2010.10.006 宣杨, 王旭, 刘承安, 等. 不完全乔列斯基分解共轭梯度法在磁感应成像三维有限元正问题中的应用[J]. 电子与信息学报, 2016, 38(1): 187–194. doi: 10.11999/JEIT150437XUAN Yang, WANG Xu, LIU Cheng’an, et al. Incomplete Cholesky conjugate gradient method for the three-dimensional forward problem in magnetic induction tomography using finite element method[J]. Journal of Electronics &Information Technology, 2016, 38(1): 187–194. doi: 10.11999/JEIT150437 魏宏安, 吴小清. 基于Maxwell有限元分析的高压输电线路安全距离研究[J]. 电气开关, 2018, 56(5): 86–90. doi: 10.3969/j.issn.1004-289X.2018.05.020WEI Hong’an and WU Xiaoqing. Research on safety distance of high voltage transmission lines based on Maxwell’s finite element analysis[J]. Electric Switcher, 2018, 56(5): 86–90. doi: 10.3969/j.issn.1004-289X.2018.05.020 -





 下载:
下载:


 下载:
下载:
