使用能量匹配的监控视频自适应速率压缩感知

王健明; 陈建华

doi:10.11999/JEIT190750

使用能量匹配的监控视频自适应速率压缩感知

doi: 10.11999/JEIT190750

王健明,
陈建华^,

云南大学信息学院昆明 650504

基金项目: 国家自然科学基金(61861045)

详细信息

作者简介:
王健明：男，1984年生，博士生，研究方向为数据压缩

陈建华：男，1964年生，教授，博士生导师，研究方向为信息传输理论与应用

通讯作者:
陈建华　chenjh@ynu.edu.cn

中图分类号: TN911.73
计量
- 文章访问数: 844
- HTML全文浏览量: 228
- PDF下载量: 99
- 被引次数: 64
出版历程
- 收稿日期: 2019-09-29
- 修回日期: 2020-09-27
- 网络出版日期: 2020-09-29
- 刊出日期: 2020-12-08

Adaptive-Rate Compressive Sensing Using Energy Matching for Monitoring Video

Jianming WANG,
Jianhua CHEN^,

School of Information Science and Engineering, Yunnan University, Kunming 650504, China

Funds: The National Natural Science Foundation of China (61861045)

摘要

摘要: 获取信号稀疏度对压缩感知(CS)性能的提升有重大意义，但在采样端不进行完整信号数字化采集和存储的情况下，对信号稀疏度进行估计比较困难。现有方法在稀疏度估计性能和计算复杂度方面难以取得较好的平衡。针对采样端对信号特性未知的监控视频应用，该文提出一种新的使用能量匹配的自适应速率压缩感知方法(ARCS-EM)，通过观测一个恒定低速率的压缩感知观测结果来对当前帧实际稀疏度进行估计，然后根据估计结果决定当前帧应执行的压缩感知测量数，再进行补充测量得到当前帧的优化压缩感知采样结果。实验结果表明，该方法可以较好地适应视频中前景稀疏度的变化，为每帧图像分配适当的压缩感知测量速率，在不显著提高采样端计算复杂度的前提下，有效提高重建视频的质量。
- 图像信号处理 /
- 压缩感知 /
- 自适应速率采样 /
- 能量匹配 /
- 监控视频
Abstract: Signal sparsity is of great significance for the improvement of Compressive Sensing (CS) performance. However, it is difficult to estimate the sparsity when the whole signal is not captured and stored at the sampling side. Few existing mothed can achieve good balance in terms of the sparsity estimation performance and the computational complexity. For the monitoring video applications where the signal characteristics is unknown for sampling devices, a new Adaptive-Rate CS using Energy Matching (ARCS-EM) method is proposed. By observing the measurement results of a low-rate compressive sensing, the actual sparsity of the current frame is estimated and then the rate of measurement for the current frame is determined. Finally, supplementary measurements are performed to obtain the optimized compressive sensing result for the current frame. Experiment results show that the proposed method could allocate suitable measurement rate for each frame to adapt to the variation of sparsity in different frames. The quality of reconstructed videos is effectively improved without noticeably increasing computational complexity in the sampling side.
- Image signal processing /
- Compressive Sensing (CS) /
- Adaptive-rate sampling /
- Energy matching /
- Monitoring video

HTML全文

图 1 视频序列范例

下载: 全尺寸图片幻灯片

图 2 测试视频稀疏程度估计表现

下载: 全尺寸图片幻灯片

图 3 测试视频采样速率

下载: 全尺寸图片幻灯片

图 4 测试视频图像重建质量

下载: 全尺寸图片幻灯片

表 1 实验参数

参数	$\varSigma$	$a$	$b$	$\tau$	$r$
视频序列Hall	2.65	16	128	8	600
视频序列PETS	2.45	16	128	8	600

下载: 导出CSV

表 2 不同方法的自适压缩感知平均性能对比

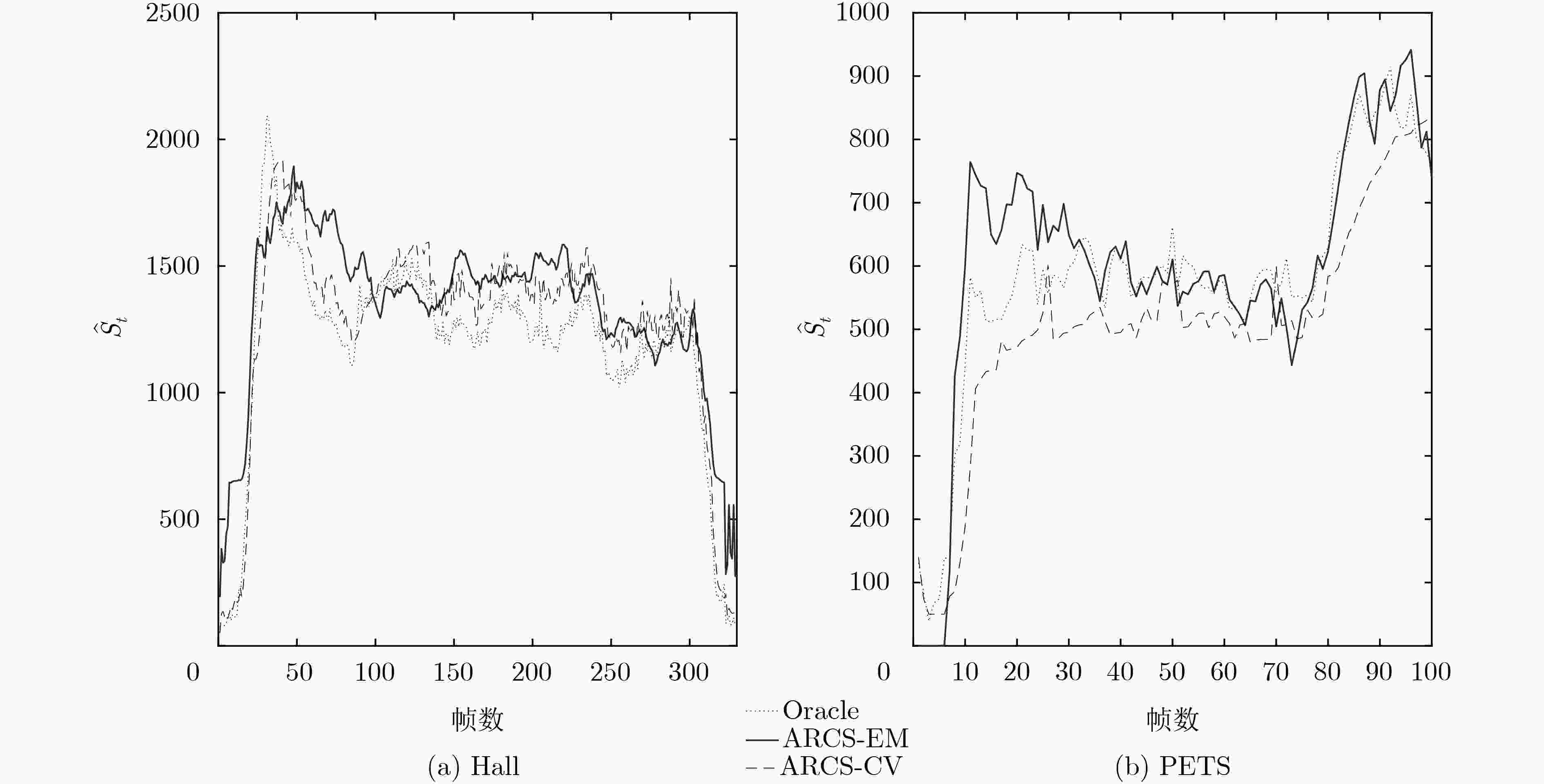
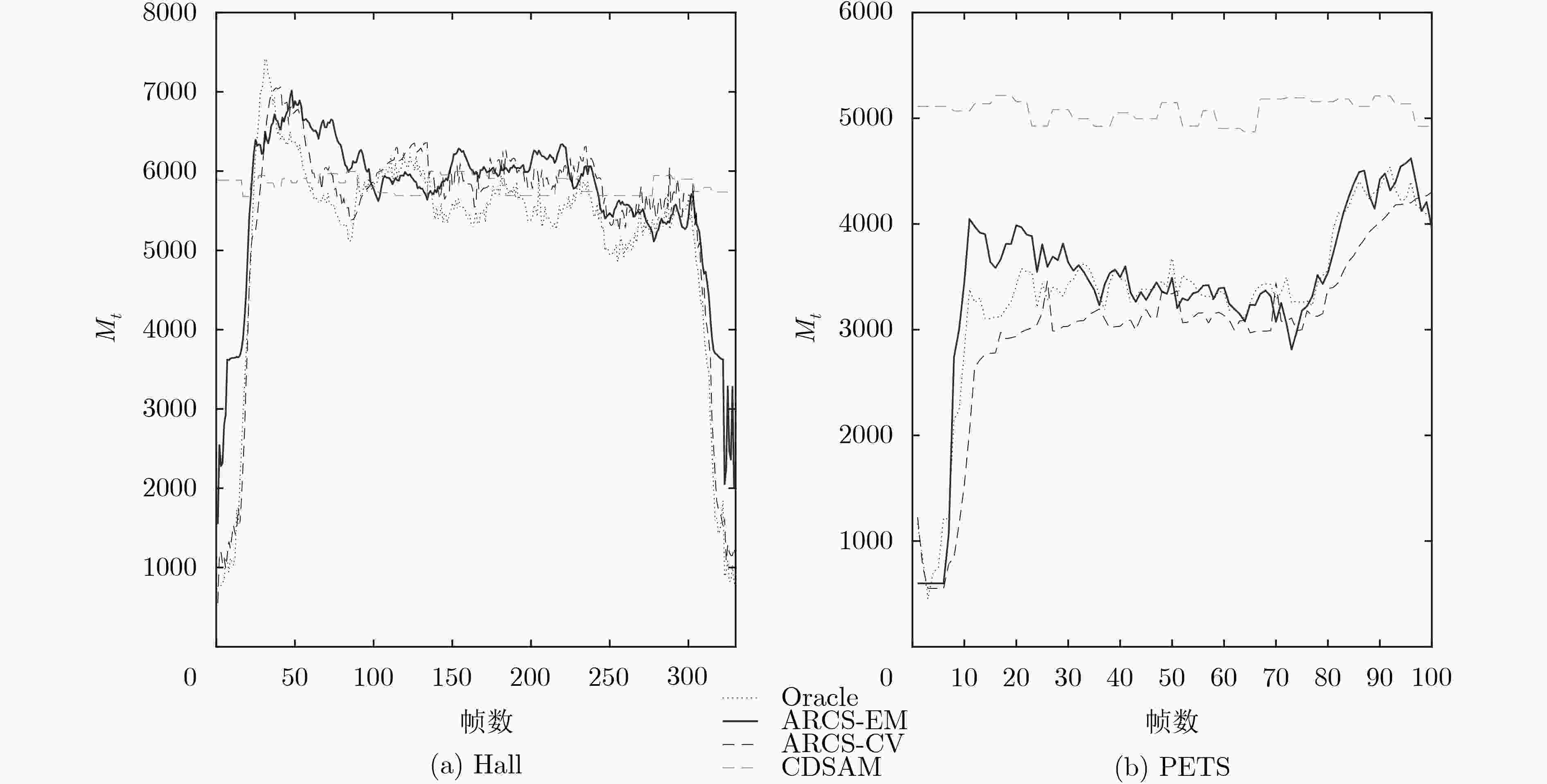
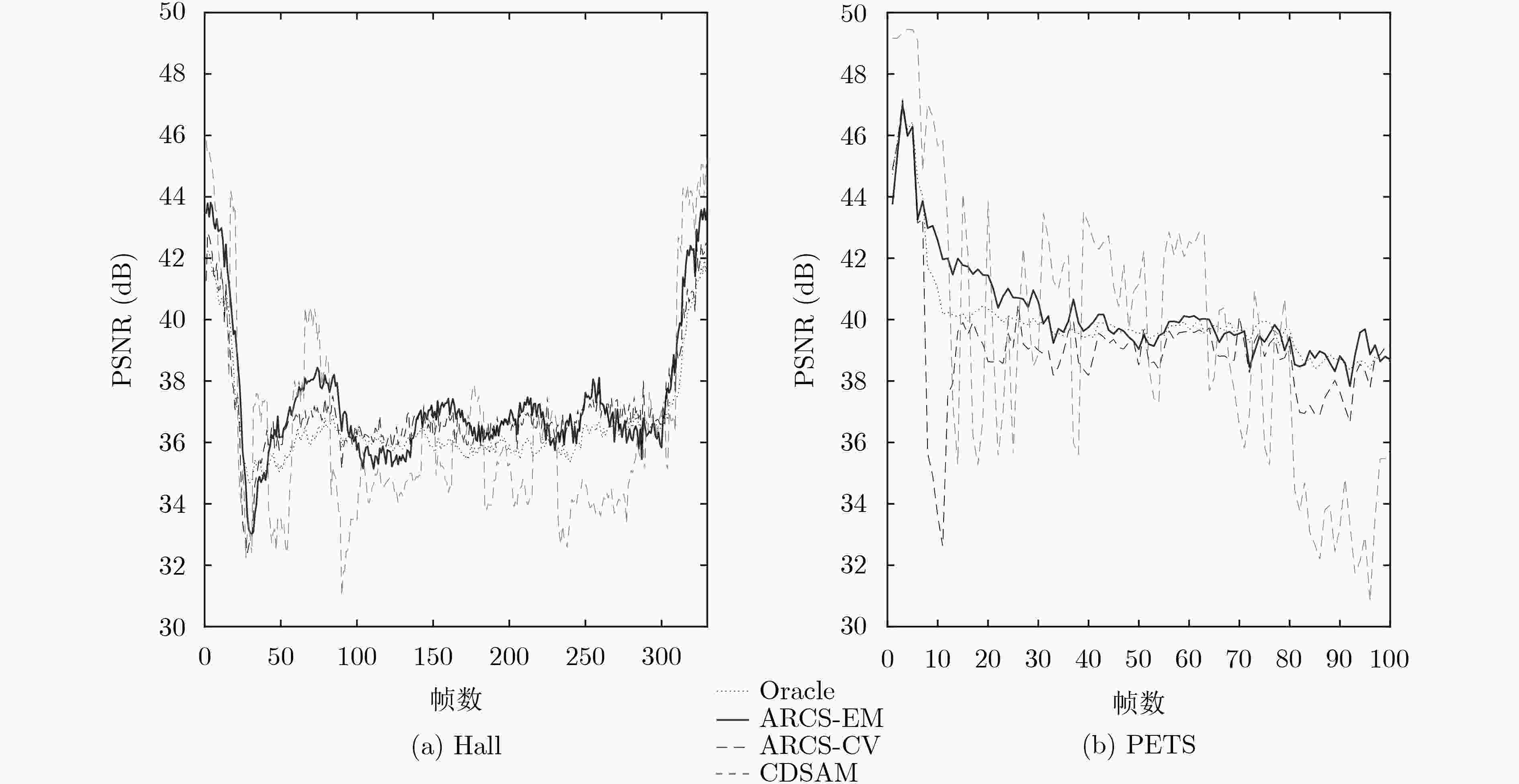
实验结果	Hall视频平均压缩感知采样率	Hall视频平均峰值信噪比(dB)	PETS视频平均压缩感知采样率	PETS视频平均峰值信噪比(dB)
Oracle	0.2040	36.59	0.1317	40.02
CDSAM方法	0.2297	36.34	0.2001	39.53
ARCS-CV方法	0.2137	37.03	0.1191	39.07
ARCS-EM方法	0.2232	37.26	0.1350	40.26

下载: 导出CSV

表 3 采样运行时间对照表(ms)

运行时间	Hall视频T₁	Hall视频T₂	Hall视频T₃	Hall视频T	PETS视频T₁	PETS视频T₂	PETS视频T₃	PETS视频T
CDSAM方法	7.48	104.18	0	111.66	6.76	94.93	0	101.69
ARCS-CV方法	957.26	0.14	2.99×10⁵	3.00×10⁵	526.56	0.11	1.44×10⁵	1.45×10⁵
ARCS-EM方法	800.87	0.42	0	801.29	498.75	0.51	0	499.26

下载: 导出CSV

参考文献(23)

CANDÈS E J, ROMBERG J, and TAO T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information[J]. IEEE Transactions on Information Theory, 2006, 52(2): 489–509. doi: 10.1109/TIT.2005.862083

DONOHO D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289–1306. doi: 10.1109/TIT.2006.871582

CANDÈS E J. The restricted isometry property and its implications for compressed sensing[J]. Comptes Rendus Mathematique, 2008, 346(9/10): 589–592. doi: 10.1016/j.crma.2008.03.014

王钢, 周若飞, 邹昳琨. 基于压缩感知理论的图像优化技术[J]. 电子与信息学报, 2020, 42(1): 222–233. doi: 10.11999/JEIT190669

WANG Gang, ZHOU Ruofei, and ZOU Yikun. Research on image optimization technology based on Compressed Sensing[J]. Journal of Electronics &Information Technology, 2020, 42(1): 222–233. doi: 10.11999/JEIT190669

杨森林, 万国宾. 联合结构预测和运动补偿的视频自适应压缩感知[J]. 西北大学学报: 自然科学版, 2019, 49(6): 909–917. doi: 10.16152/j.cnki.xdxbzr.2019-06-010

YANG Senlin and WAN Guobin. Adaptive compressed sensing of video by combining structural predictions and motion compensation[J]. Journal of Northwest University:Natural Science Edition, 2019, 49(6): 909–917. doi: 10.16152/j.cnki.xdxbzr.2019-06-010

SHAHRASBI B and RAHNAVARD N. Model-based nonuniform Compressive Sampling and recovery of natural images utilizing a Wavelet-domain universal hidden Markov model[J]. IEEE Transactions on Signal Processing, 2017, 65(1): 95–104. doi: 10.1109/TSP.2016.2614654

LAKSHMI T C S, GNANADURAI D, and MUTHULAKSHMI I. Energy conserving texture-based adaptable Compressive Sensing scheme for WVSN[J]. Concurrency and Computation: Practice and Experience, 2019: e5178. doi: 10.1002/cpe.5178

ZHANG Xufan, WANG Yong, WANG Dianhong, et al. Adaptive image compression based on compressive sensing for video sensor nodes[J]. Multimedia Tools and Applications, 2018, 77(11): 13679–13699. doi: 10.1007/s11042-017-4981-6

DUARTE M F, DAVENPORT M A, TAKHAR D, et al. Single-pixel imaging via compressive sampling[J]. IEEE Signal Processing Magazine, 2008, 25(2): 83–91. doi: 10.1109/msp.2007.914730

范剑英, 马明阳, 赵首博. 基于压缩感知高反光成像技术研究[J]. 电子与信息学报, 2020, 42(4): 1013–1020. doi: 10.11999/JEIT190512

FAN Jianying, MA Mingyang, and ZHAO Shoubo. Research on high reflective imaging technology based on compressed sensing[J]. Journal of Electronics &Information Technology, 2020, 42(4): 1013–1020. doi: 10.11999/JEIT190512

吴新杰, 闫诗雨, 徐攀峰, 等. 基于稀疏度自适应压缩感知的电容层析成像图像重建算法[J]. 电子与信息学报, 2018, 40(5): 1250–1257. doi: 10.11999/JEIT170794

WU Xinjie, YAN Shiyu, XU Panfeng, et al. Image reconstruction algorithm for electrical capacitance tomography based on sparsity adaptive Compressed Sensing[J]. Journal of Electronics &Information Technology, 2018, 40(5): 1250–1257. doi: 10.11999/JEIT170794

SHANGGUAN Wentao, YAN Qiurong, WANG Hui, et al. Adaptive single photon compressed imaging based on constructing a smart threshold matrix[J]. Sensors, 2018, 18(10): 3449. doi: 10.3390/s18103449

YUAN Xin, YANG Jianbo, LLULL P, et al. Adaptive temporal compressive sensing for video[C]. 2013 IEEE International Conference on Image Processing, Melbourne, Australia, 2013: 14–18. doi: 10.1109/ICIP.2013.6738004.

WANG Yeru, TANG Chaoying, CHEN Yueting, et al. Adaptive temporal Compressive Sensing for video with motion estimation[J]. Optical Review, 2018, 25(2): 215–226. doi: 10.1007/s10043-018-0408-5

练秋生, 田天, 陈书贞, 等. 基于变采样率的多假设预测分块视频压缩感知[J]. 电子与信息学报, 2013, 35(1): 203–208. doi: 10.3724/SP.J.1146.2012.00590

LIAN Qiusheng, TIAN Tian, CHEN Shuzhen, et al. Block compressed sensing of video based on variable sampling rates and multihypothesis predictions[J]. Journal of Electronics &Information Technology, 2013, 35(1): 203–208. doi: 10.3724/SP.J.1146.2012.00590

LI Honggui. Compressive domain spatial–temporal difference saliency-based realtime adaptive measurement method for video recovery[J]. IET Image Processing, 2019, 13(11): 2008–2017. doi: 10.1049/iet-ipr.2019.0116

WARNELL G, BHATTACHARYA S, CHELLAPPA R, et al. Adaptive-rate compressive sensing using side information[J]. IEEE Transactions on Image Processing, 2015, 24(11): 3846–3857. doi: 10.1109/TIP.2015.2456425

DUARTE-CARVAJALINO J M, YU Guoshen, CARIN L, et al. Task-driven adaptive statistical compressive sensing of Gaussian mixture models[J]. IEEE Transactions on Signal Processing, 2013, 61(3): 585–600. doi: 10.1109/TSP.2012.2225054

VAN DER BERG E and FRIEDLANDER M P. Probing the Pareto Frontier for basis pursuit solutions[J]. SIAM Journal on Scientific Computing, 2009, 31(2): 890–912. doi: 10.1137/080714488

DONOHO D L and TANNER J. Precise undersampling theorems[J]. Proceedings of the IEEE, 2010, 98(6): 913–924. doi: 10.1109/jproc.2010.2045630

CEVHER V, SANKARANARAYANAN A, DUARTE M F, et al. Compressive sensing for background subtraction[C]. The 10th European Conference on Computer Vision, France, Marseille, 2008: 155–168. doi: 10.1007/978-3-540-88688-4_12.

WARD R. Compressed sensing with cross validation[J]. IEEE Transactions on Information Theory, 2009, 55(12): 5773–5782. doi: 10.1109/tit.2009.2032712

JOHNSON W B and LINDENSTRAUSS J. Extensions of Lipschitz mappings into a Hilbert space[J]. Contemporary Mathematics, 1984, 26(12): 189–206. doi: 10.1090/conm/026/737400

施引文献

期刊类型引用(21)

1.	李民，郭琳，姚雄. 优化高斯过程回归在太阳能集热效率预测上的应用. 电网与清洁能源. 2023(08): 127-131+138 . 百度学术
2.	Han-shan Li. Recognition model and algorithm of projectiles by combining particle swarm optimization support vector and spatial-temporal constrain. Defence Technology. 2023(09): 273-283 . 必应学术
3.	何旭，席佩瑶，辛云宏. 基于代价敏感思想和自适应增强集成的SVM多分类算法. 微型电脑应用. 2023(09): 1-3 . 百度学术
4.	徐红先，张书玮. 基于极限学习机及多姿态信息融合的步态识别. 机械. 2023(11): 72-80 . 百度学术
5.	陈晓禾，曹旭刚，陈健生，胡春华，马羽. 基于三维卷积的帕金森患者拖步识别. 电子与信息学报. 2021(12): 3467-3475 . 本站查看
6.	雷建超，刘栋博，房玉，庄祖江，刘俊豪. 基于表面肌电信号的性别差异性手势识别. 中国医学物理学杂志. 2020(03): 337-341 . 百度学术
7.	金鑫，冯毅，尤雪汐，王佳欣. 基于机器学习的信息安全设备调配保障技术研究. 电子科技. 2020(08): 80-86 . 百度学术
8.	孟明，闫冉，高云园，佘青山. 基于多元变分模态分解的脑电多域特征提取方法. 传感技术学报. 2020(06): 853-860 . 百度学术
9.	王志芳，王书涛，王贵川. 粒子群优化BP神经网络在甲烷检测中的应用. 光子学报. 2019(04): 147-154 . 百度学术
10.	邹倩颖，王小芳. 粒子群优化BP神经网络在步态识别中的研究. 实验技术与管理. 2019(08): 130-133+138 . 百度学术
11.	郭海山，高波涌，陆慧娟. 基于Boruta-PSO-SVM的股票收益率研究. 传感器与微系统. 2018(03): 51-53+57 . 百度学术
12.	周长林，钱志升，王勤民，余道杰，程俊平. 基于PSO-SVM方法的电源线传导泄漏信号识别与还原. 电子与信息学报. 2018(09): 2206-2211 . 本站查看
13.	赵荣建，汤敏芳，陈贤祥，杜利东，曾华林，赵湛，方震. 基于光纤传感的生理参数监测系统研究. 电子与信息学报. 2018(09): 2182-2189 . 本站查看
14.	胡长俊，袁树杰. 煤矿井下WSN中基于自适应粒子群聚类算法的多sink节点部署. 计算机科学. 2018(11): 103-107+123 . 百度学术
15.	王秀娟，相从斌. 基于累积量的DoS攻击检测算法. 北京工业大学学报. 2017(09): 1328-1334 . 百度学术
16.	杜必强，孙立江. 基于PSO-SVM模型的焊接转子环焊缝超声缺陷识别. 动力工程学报. 2017(05): 379-385 . 百度学术
17.	赵湛，韩璐，方震，陈贤祥，杜利东，刘正奎. 基于可穿戴设备的日常压力状态评估研究. 电子与信息学报. 2017(11): 2669-2676 . 本站查看
18.	董广宇. 基于多特征融合的复杂路况步态识别方法. 科学技术与工程. 2017(08): 202-207 . 百度学术
19.	韩笑，佘青山，高云园，罗志增. 基于NA-MEMD和互信息的脑电特征提取方法. 传感技术学报. 2016(08): 1140-1148 . 百度学术
20.	黄成泉，王士同，蒋亦樟，董爱美. v-软间隔罗杰斯特回归分类机. 电子与信息学报. 2016(04): 985-992 . 本站查看
21.	徐超立，林科，杨晨，吴超华，高小榕. 基于小腿表面肌电的智能机器人协同控制方法. 中国生物医学工程学报. 2016(04): 385-393 . 百度学术