GTD Model Parameters Estimation and RCS Reconstruction Based on the Improved LS-ESPRIT Algorithm
-
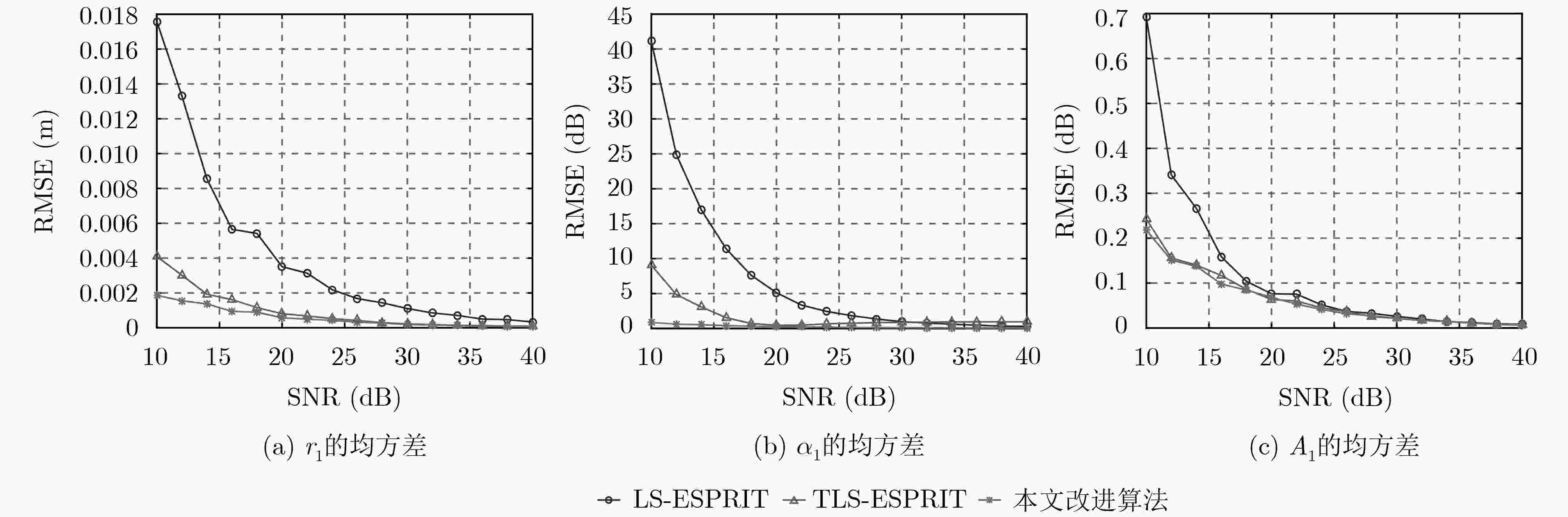
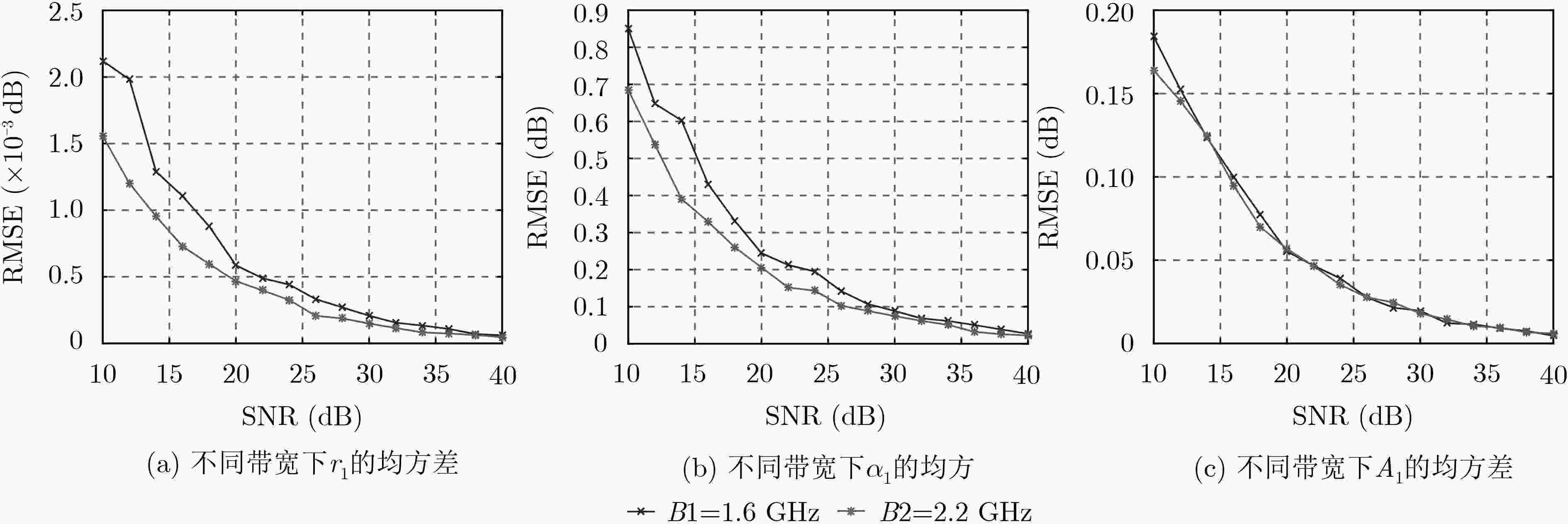
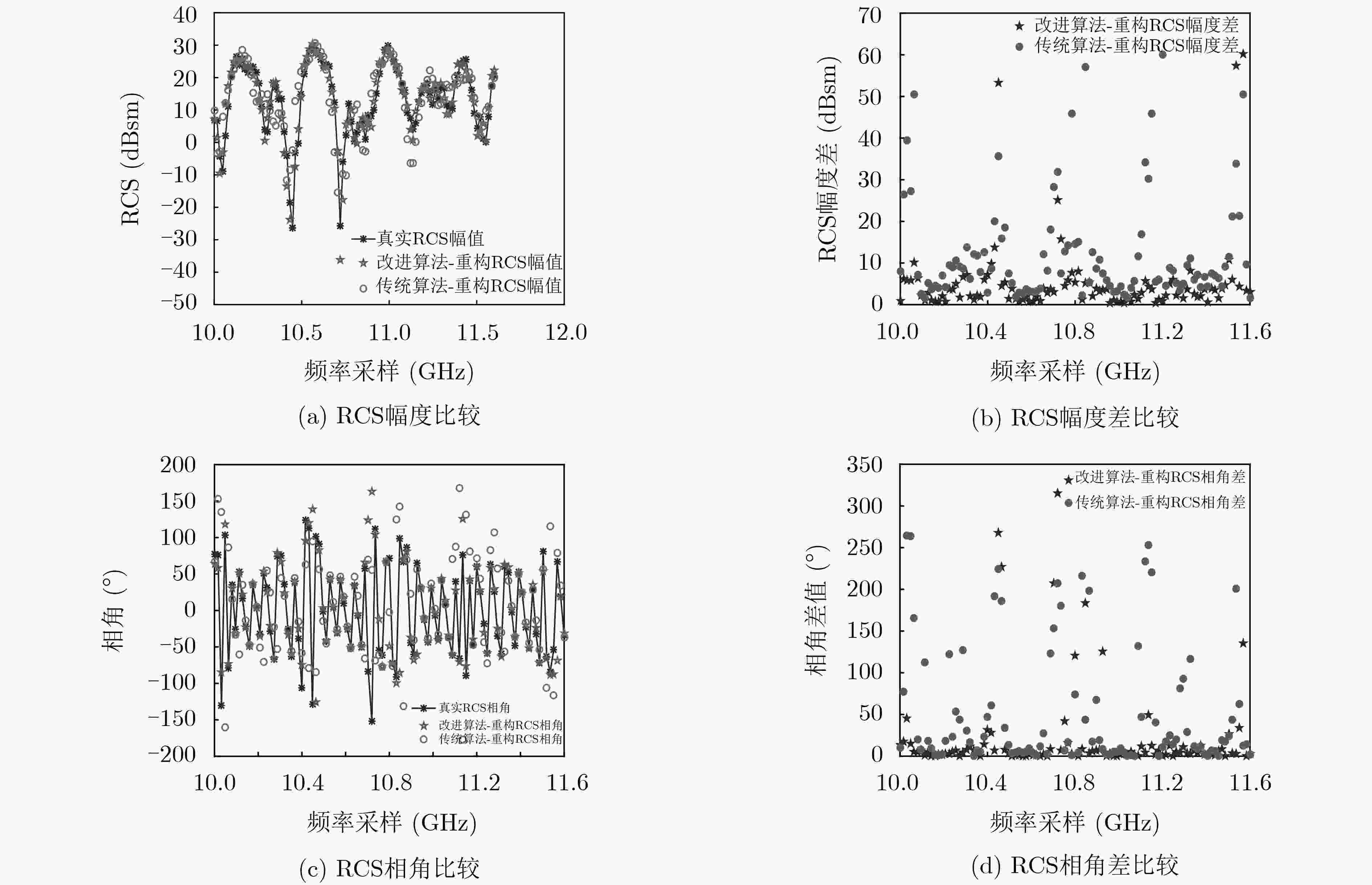
摘要: 针对传统LS-ESPRIT算法在估计GTD模型参数时抗噪效果差,估计精度不高这一问题,该文提出了一种改进的LS-ESPRT算法,有效地提高了算法的参数估计性能与抗噪性。首先,根据雷达目标的回波数据构建Hankel矩阵;其次,采用核范数凸优化方法对上述Hankel矩阵进行降噪处理,得到低秩的重构Hankel矩阵;最后,利用传统的LS-ESPRIT算法对降噪后的数据进行处理,估计出GTD模型参数。基于改进算法与传统算法分别得到重构RCS,并针对不同带宽对参数估计精度的影响作以仿真探究。仿真结果表明,与传统LS-ESPRIT算法与传统TLS-ESPRIT算法相比,改进LS-ESPRIT算法的参数估计性能更高,抗噪性更强,且重构RCS的幅值与相角误差更小。对不同带宽下的参数估计精度也进行了探究,并得出:带宽越大,估计精度越高。
-
关键词:
- 散射中心 /
- GTD模型 /
- 凸优化处理 /
- 改进的LS-ESPRIT算法 /
- RCS重构
Abstract: The traditional Least Squares-Estimating Signal Parameter via Rotational Invariance Techniques (LS-ESPRIT) algorithm is not effective while estimating parameters of the Geometric Theory of Diffraction (GTD) at lower SNR. To solve this problem, an improved LS-ESPRIT algorithm is proposed in this paper. Firstly, a Hankel matrix is constructed by the echo data of radar targets.Secondly,a low- rank reconstructed Hankel matrix is obtained,which is solved by the nuclear norm convex optimization method. Finally, the traditional LS-ESPRIT algorithm is used to process the data after noise reduction and estimate the parameters of the GTD model. Moreover,the reconstructed Radar Cross Section (RCS) can be obtained by the traditional LS-ESPRIT algorithm and the improved LS-ESPRIT algorithm. The influence of different bandwidths on parameter estimation is also analyzed in this paper. Simulation results show that the estimation accuracy and noise resistance of the improved LS-ESPRIT algorithm is better than the traditional LS-ESPRIT algorithm and the traditional TLS-ESPRIT algorithm. Furthermore, the amplitude error and phase angle error of the RCS which is reconstructed by the improved algorithm are smaller than the traditional algorithm. Different bandwidths also have influences on parameter estimation accuracy, the more wider bandwidth is, the more accurate parameters can be estimated. -
表 1 典型散射结构的
${\alpha _i}$ 取值典型散射结构 ${\alpha _i}$取值 二面角、三面角、平面法向反射 1.0 单曲面反射、圆柱面反射 0.5 双曲面反射、球面反射 0 边缘绕射 –0.5 尖顶绕射 –1.0 表 2 散射中心参数值
序号 位置${r_i}({\rm{m}})$ 类型${\alpha _i}$ 强度${A_i}$ 1 1.200 1.000 6.112 2 1.400 0.500 5.398 3 1.900 0 4.234 4 2.300 1.000 3.102 -
DING Baiyuan and WEN Gongjian. A region matching approach based on 3-D scattering center model with application to SAR target recognition[J]. IEEE Sensors Journal, 2018, 18(11): 4623–4632. doi: 10.1109/JSEN.2018.2828307 ZHONG Jinrong, WEN Gongjian, HUI Bingwei, et al. Three-dimensional positions of scattering centers reconstruction from multiple SAR images based on radargrammetry[J]. Journal of Central South University, 2015, 22(5): 1776–1789. doi: 10.1007/s11771-015-2696-2 HE Yang, HE Siyuan, ZHANG Yunhua, et al. A forward approach to establish parametric scattering center models for known complex radar targets applied to SAR ATR[J]. IEEE Transactions on Antennas and Propagation, 2014, 62(12): 6192–6205. doi: 10.1109/TAP.2014.2360700 LI Tingli and DU Lan. SAR automatic target recognition based on attribute scattering center model and discriminative dictionary Learning[J]. IEEE Sensors Journal, 2019, 19(12): 4598–4611. doi: 10.1109/JSEN.2019.2901050 许少坤, 刘记红, 袁翔宇. 基于HRRP序列的中段目标二维几何特征反演方法[J]. 电子与信息学报, 2017, 39(10): 2366–2373. doi: 10.11999/JEIT161303XU Shaokun, LIU Jihong, and YUAN Xiangyu. Two-dimensional geometric feature inversion method for midcourse target based on HRRPs[J]. Journal of Electronics &Information Technology, 2017, 39(10): 2366–2373. doi: 10.11999/JEIT161303 ZHOU Jianxiong, SHI Zhiguang, CHENG Xiao, et al. Automatic target recognition of SAR images based on global scattering center model[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(10): 3713–3729. doi: 10.1109/tgrs.2011.2162526 CHEN Xuan, WAN Baoquan, ZHAO Tao, et al. Parameter estimation of three-dimensional scattering centers based on state space and ESPRIT method[J]. Procedia Computer Science, 2019, 147: 435–440. doi: 10.1016/j.procs.2019.01.261 郑舒予, 张小宽, 刘铭, 等. 基于一维散射中心模型的RCS频率全角度外推[J]. 空军工程大学学报: 自然科学版, 2020, 20(6): 79–83.ZHENG Shuyu, ZHANG Xiaokuan, LIU Ming, et al. RCS frequency full angle extrapolation based on one-dimensional scattering center model[J]. Journal of Air Force Engineering University:Natural Science Edition, 2020, 20(6): 79–83. 毕严先, 魏少明, 王俊, 等. 基于多假设跟踪的散射点关联和三维重构方法[J]. 北京航空航天大学学报, 2016, 42(6): 1219–1227.BI Yanxian, WEI Shaoming, WANG Jun, et al. New method of scatterers association and 3D reconstruction based on multi-hypothesis tracking[J]. Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(6): 1219–1227. 王昕, 郭宝峰, 尚朝轩. 基于二维ISAR图像序列的雷达目标三维重建方法[J]. 电子与信息学报, 2013, 35(10): 2475–2480. doi: 10.3724/SPJ1146.2013.00140WANG Xin, GUO Baofeng, and SHANG Chaoxuan. 3D reconstruction of target geometry based on 2D data of inverse synthetic aperture radar images[J]. Journal of Electronics &Information Technology, 2013, 35(10): 2475–2480. doi: 10.3724/SPJ1146.2013.00140 张磊, 何思远, 朱国强, 等. 雷达目标三维散射中心位置正向推导和分析[J]. 电子与信息学报, 2018, 40(12): 2854–2860. doi: 10.11999/JEIT180115ZHANG Lei, HE Siyuan, ZHU Guoqiang, et al. Forward derivation and analysis for 3-D scattering center position of radar target[J]. Journal of Electronics &Information Technology, 2018, 40(12): 2854–2860. doi: 10.11999/JEIT180115 HURST M and MITTRA R. Scattering center analysis via Prony’s method[J]. IEEE Transactions on Antennas and Propagation, 1987, 35(8): 986–988. doi: 10.1109/TAP.1987.1144210 POTTER L C, CHIANG D M, CARRIER R, et al. A GTD-based parametric model for radar scattering[J]. IEEE Transactions on Antennas and Propagation, 1995, 43(10): 1058–1067. doi: 10.1109/8.467641 王菁, 周建江, 汪飞. 基于GTD模型的目标二维散射中心提取[J]. 电子与信息学报, 2009, 31(4): 958–962.WANG Jing, ZHOU Jianjiang, and WANG Fei. 2D scattering centers extraction of objects based on GTD model[J]. Journal of Electronics &Information Technology, 2009, 31(4): 958–962. PARIKH N and BOYD S. Proximal algorithms[J]. Foundations and Trends® in Optimization, 2014, 1(3): 127–239. doi: 10.1561/2400000003 YAN Xingwei, HU Jiemin, ZHAO Ge, et al. A new parametric estimation method for GTD model based on modified compressed sensing[J]. Progress in Electromagnetics Research, 2013, 141: 553–575. doi: 10.2528/PIER13052017 庄钊文, 王雪松, 黎湘, 等. 雷达目标识别[M]. 北京: 高等教育出版社, 2014: 193–200.ZHUANG Zhaowen, WANG Xuesong, LI Xiang, et al. Radar Target Recognition[M]. Beijing: Higher Education Press, 2014: 193–200. 张贤达. 现代信号处理[M]. 北京: 清华大学出版社, 2002: 56–60.ZHANG Xianda. Modern Signal Processing[M]. Beijing: Tsinghua University Press, 2002: 56–60. FAZEL M, HINDI H, and BOYD S P. A rank minimization heuristic with application to minimum order system approximation[C]. Proceedings of 2001 American Control Conference, Arlington, 2001: 4734–4739. FAZEL M. Matrix rank minimization with applications[D]. [Ph.D. dissertation], Stanford University, 2002: 27–46. -






 下载:
下载:



 下载:
下载:
