A Distributed Elastic Net Regression Algorithm for Private Data Analytics in Internet of Things
-
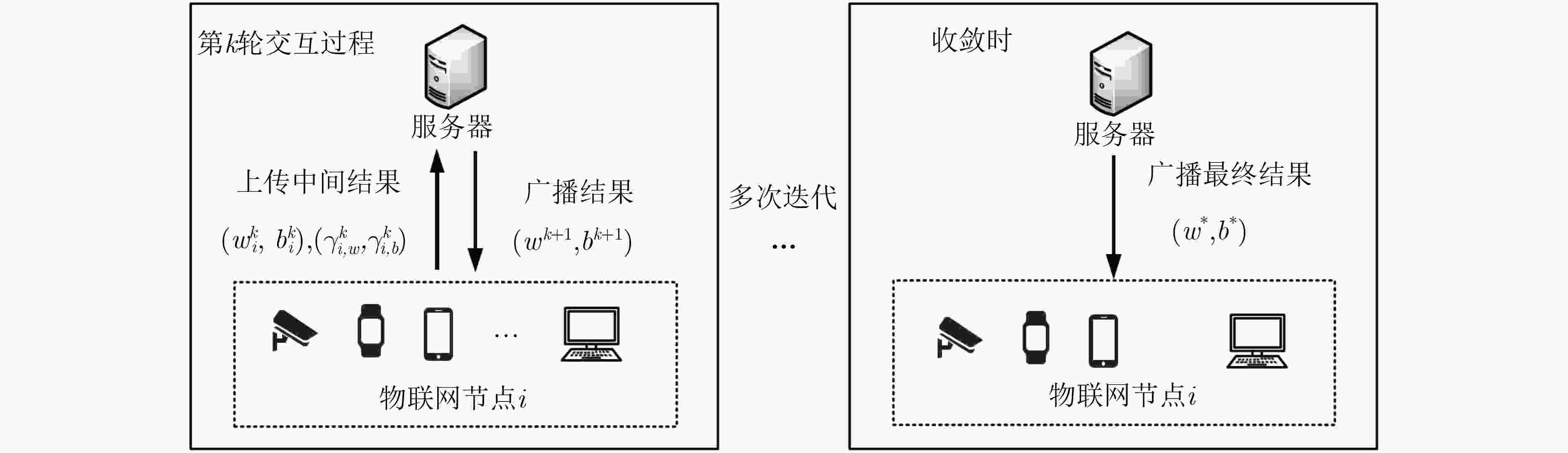
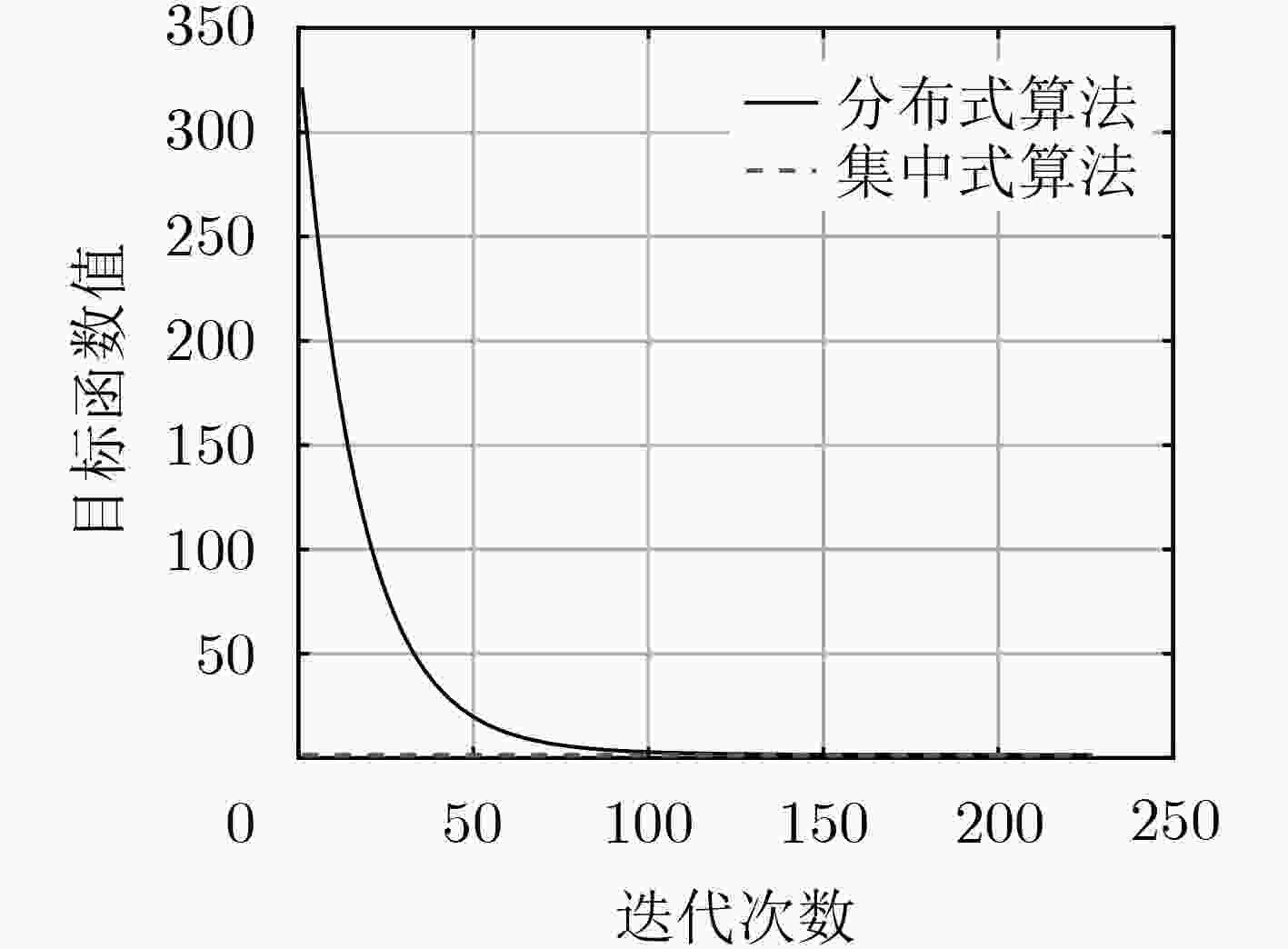
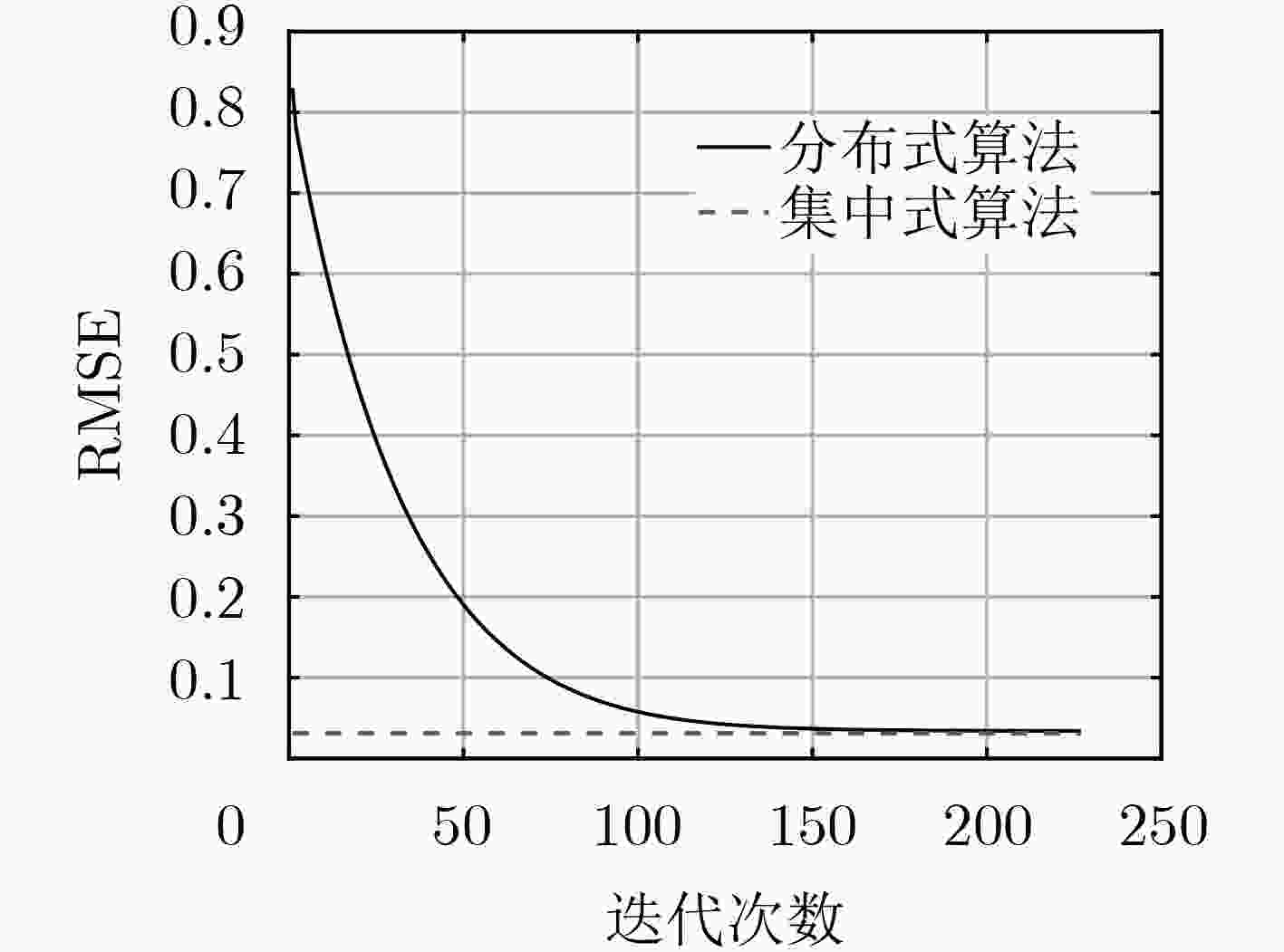
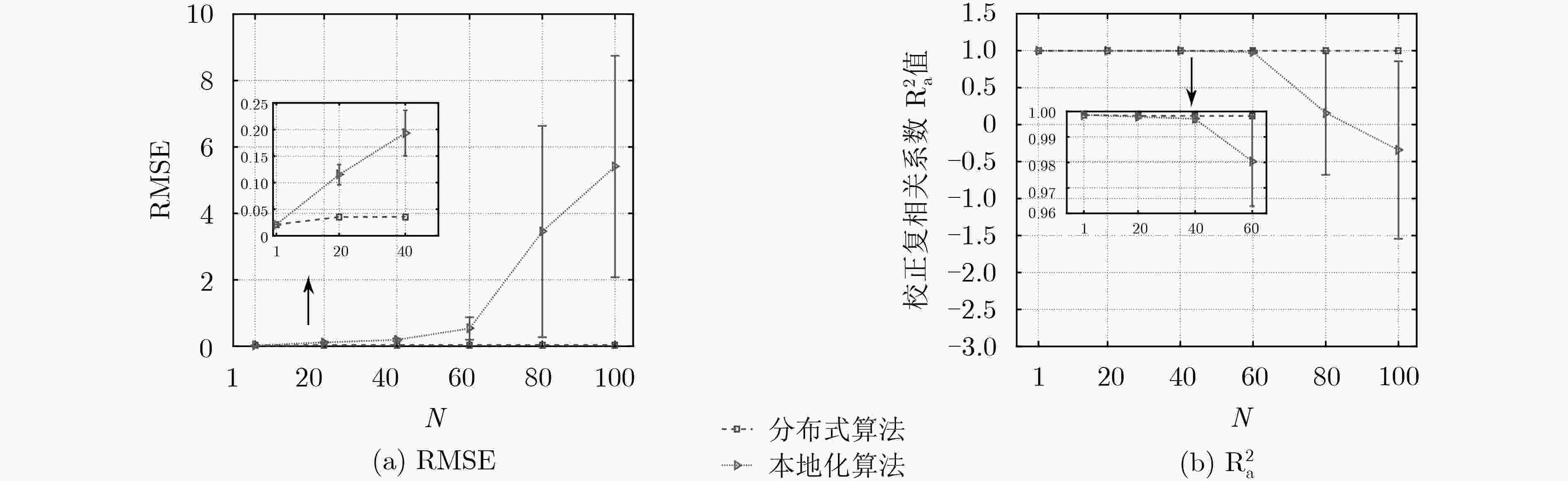
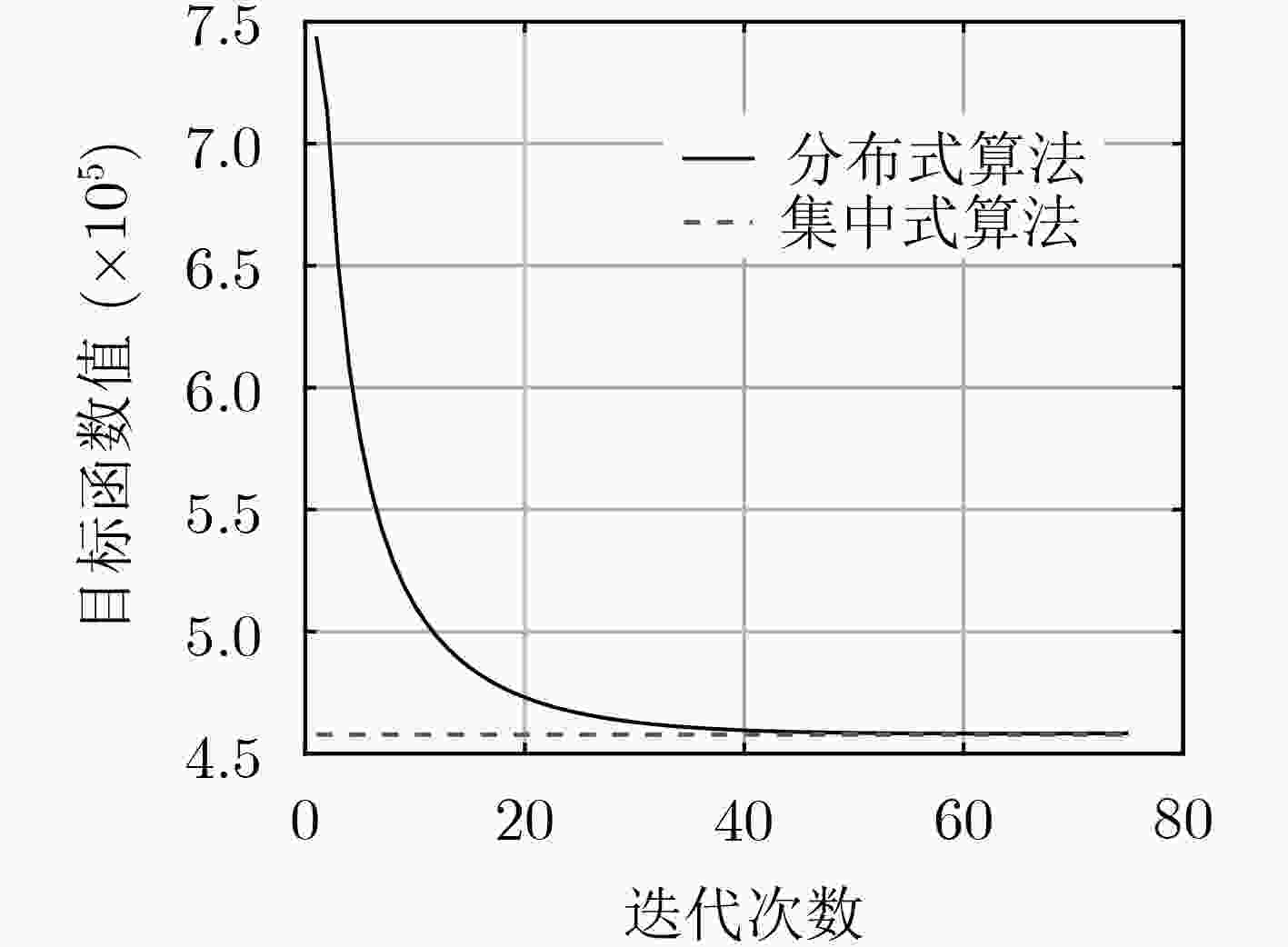
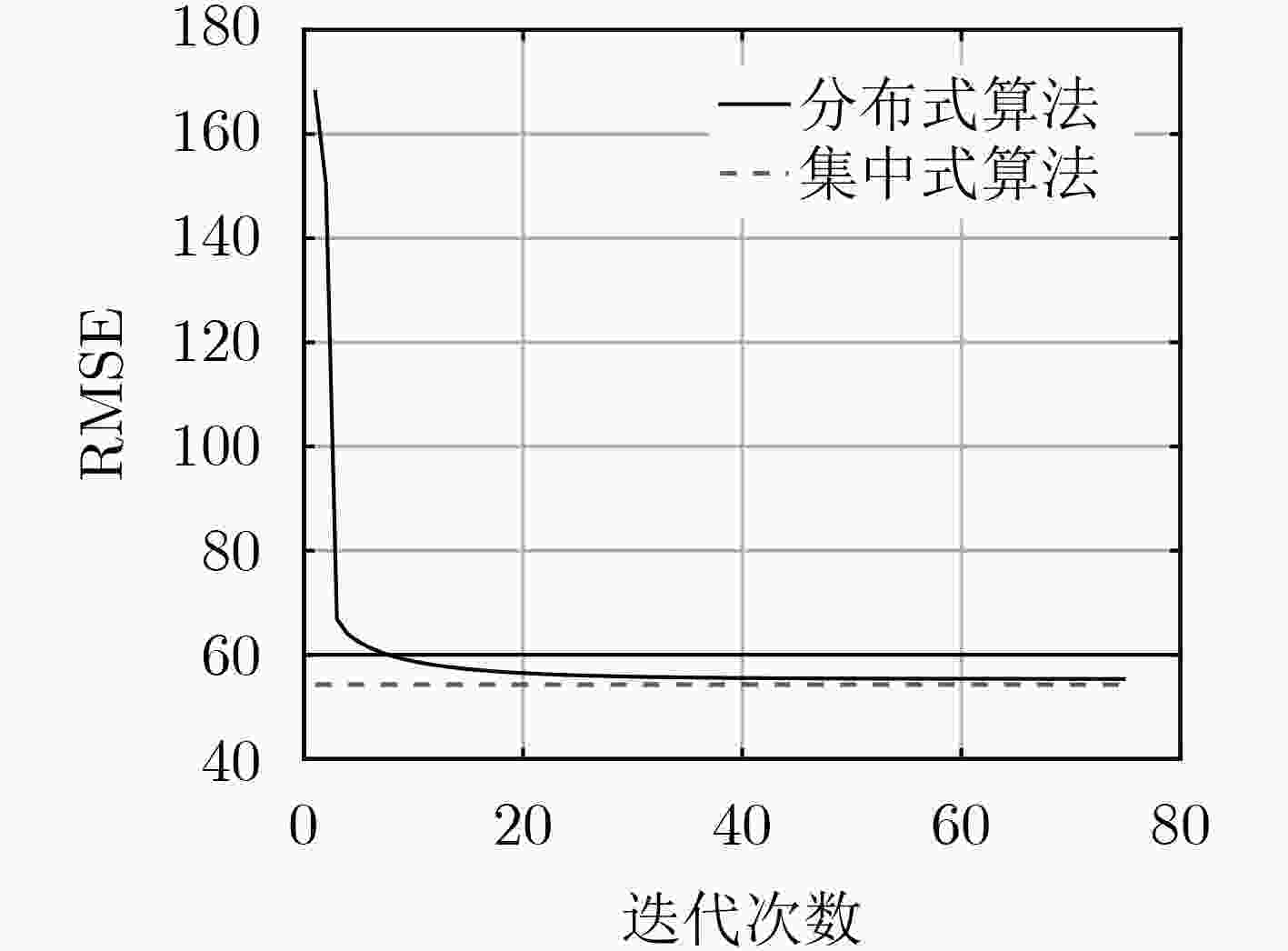
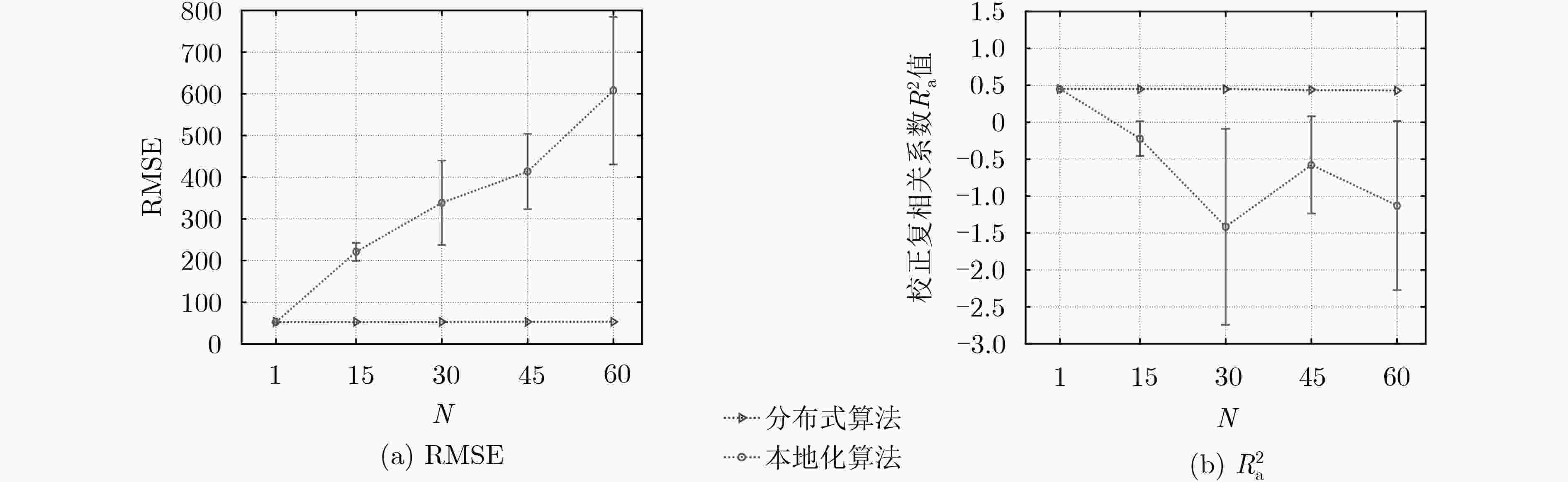
摘要: 为了解决基于集中式算法的传统物联网数据分析处理方式易引发网络带宽压力过大、延迟过高以及数据隐私安全等问题,该文针对弹性网络回归这一典型的线性回归模型,提出一种面向物联网(IoT)的分布式学习算法。该算法基于交替方向乘子法(ADMM),将弹性网络回归目标优化问题分解为多个能够由物联网节点利用本地数据进行独立求解的子问题。不同于传统的集中式算法,该算法并不要求物联网节点将隐私数据上传至服务器进行训练,而仅仅传递本地训练的中间参数,再由服务器进行简单整合,以这样的协作方式经过多轮迭代获得最终结果。基于两个典型数据集的实验结果表明:该算法能够在几十轮迭代内快速收敛到最优解。相比于由单个节点独立训练模型的本地化算法,该算法提高了模型结果的有效性和准确性;相比于集中式算法,该算法在确保计算准确性和可扩展性的同时,可有效地保护个体隐私数据的安全性。Abstract: In order to solve the problems caused by the traditional data analysis based on the centralized algorithm in the IoT, such as excessive bandwidth occupation, high communication latency and data privacy leakage, considering the typical linear regression model of elastic net regression, a distributed learning algorithm for Internet of Things (IoT) is proposed in this paper. This algorithm is based on the the Alternating Direction Method of Multipliers (ADMM) framework. It decomposes the objective problem of elastic net regression into several sub-problems that can be solved independently by each IoT node using its local data. Different from traditional centralized algorithms, the proposed algorithm does not require the IoT node to upload its private data to the server for training, but rather the locally trained intermediate parameters to the server for aggregation. In such a collaborative manner, the server can finally obtain the objective model after several iterations. The experimental results on two typical datasets indicate that the proposed algorithm can quickly converge to the optimal solution within dozens of iterations. As compared to the localized algorithm in which each node trains the model solely based on its own local data, the proposed algorithm improves the validity and the accuracy of training models; as compared to the centralized algorithm, the proposed algorithm can guarantee the accuracy and the scalability of model training, and well protect the individual private data from leakage.
-
表 1 PRP共轭梯度算法流程
输入:特征向量${{{x}}_{ij}}$;相应变量${y_{ij}}$;服务器提供的参数$\alpha = \left\{ {({{{w}}^{k + 1}},{b^{k + 1}})} \right\}$;对偶变量${\gamma ^k} = \{ ({\gamma _{i,w}}^k,{\gamma _{i,b}}^k)\} $; $b_i^*$; 输出:物联网节点i的局部最优解${{{w}}_i}^*$; (1) 初始迭代次数$t = 0$,初始向量${{{w}}_i}^0 = 0$,收敛精度$\varepsilon = 1e - 5$,初始搜索方向${{{p}}^0} = - g({{{w}}_i}^0)$; (2) repeat /*算法进行迭代*/ (3) for j = –1:2:1 (4) if $F({w_i}^t + {\lambda ^t}{{{p}}^t}) > F({{{w}}_i}^t + j * {{{p}}^t})$ then (5) ${\lambda ^t} \leftarrow j$; (6) end if (7) end for (8) ${{{w}}_i}^{t + 1} \leftarrow {{{w}}_i}^t + {\lambda ^t}{{{p}}^t}$;
(9) ${\beta ^t} \leftarrow \dfrac{ {g{ {({ {{w} }_i}^{t + 1})}^{\rm{T} } }(g({ {{w} }_i}^{t + 1}) - g({ {{w} }_i}^t))} }{ {g{ {({ {{w} }_i}^t)}^{\rm{T} } }g({ {{w} }_i}^t)} }$;(10) ${{{p}}^{t + 1}} = - g({{{w}}_i}^{t + 1}) + {\beta ^t}{{{p}}^t}$; (11) $t \leftarrow t + 1$; (12) until $\left\| {g({ {{w} }_i}^t)} \right\| \le \varepsilon$; /*算法达到收敛准则,停止迭代*/ (13) ${{{w}}_i}^* \leftarrow {{{w}}_i}^t$; 表 2 分布式弹性网络回归学习算法流程
输入:物联网节点的样本数据,包括特征向量${{{x}}_{ij}}$;相应因变量${y_{ij}}$; 输出:最终结果$\alpha = \left\{ {({{{w}}^*},{b^*})} \right\}$; (1) 服务器初始参数设置:$k = 0,\;\;\overline w = 0,\;\;{\overline b ^0} = 0,\;\;{\varepsilon ^{{\rm{rel}}}} = 1e - 2,\;\;{\varepsilon ^{{\rm{abs}}}} = 1e - 4$; (2) 物联网节点i参数设置: $k = 0,\gamma _{i,w}^0 = 0,\gamma _{i,b}^0 = 0$; (3)Repeat /*算法进行迭代*/ (4) 服务器整合物联网节点上传的中间参数$\left( {{{w}}_i^k,b_i^k} \right)$及$\left( {\gamma _{i,w}^k,\gamma _{i,b}^k} \right)$,求得各变量均值${\overline {{w}} ^k},{\overline b ^k},{\overline {{\gamma _w}} ^k},{\overline {{\gamma _b}} ^k}$,根据式(12)和式(13)更新参数
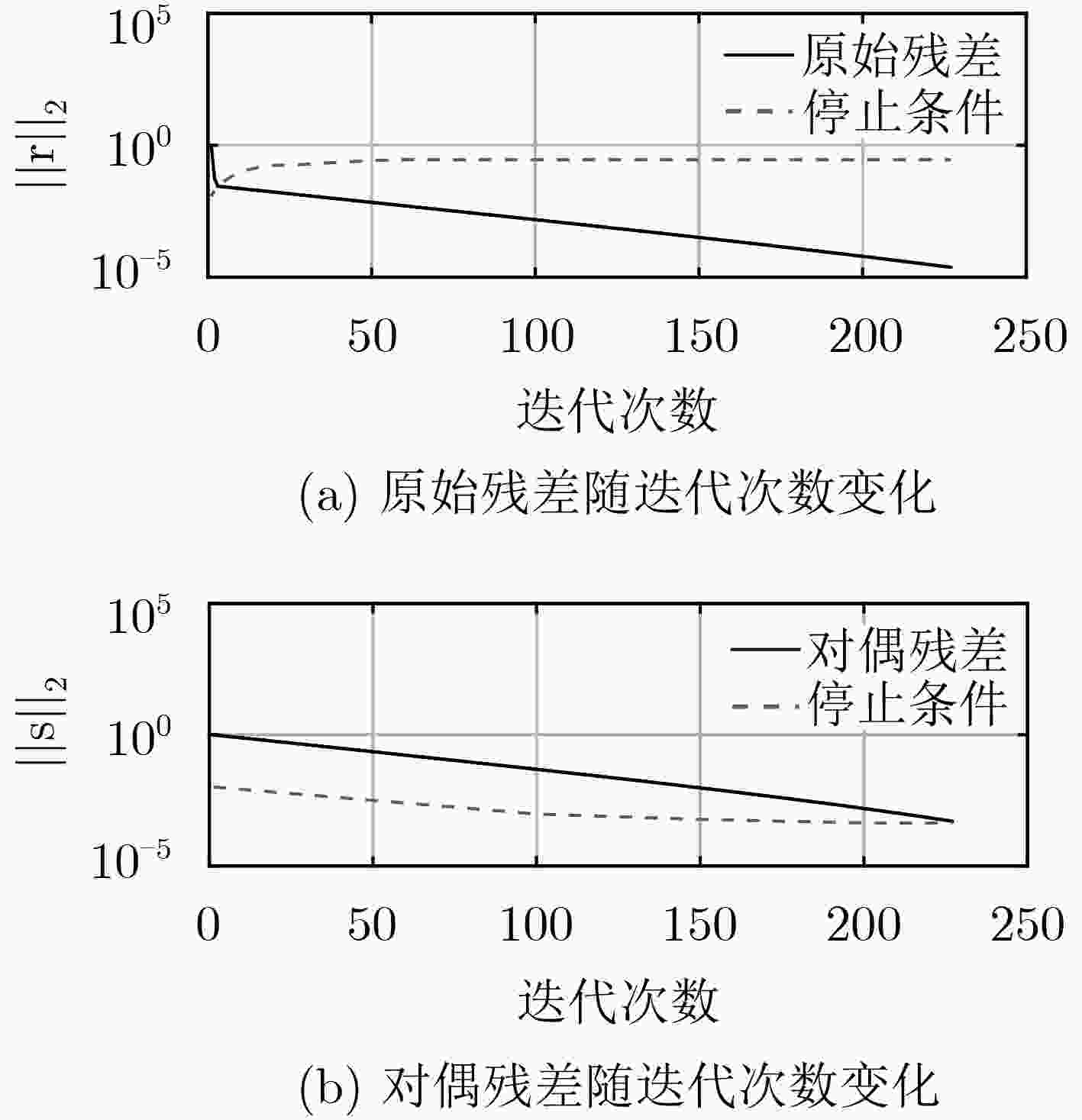
$\left( {{{{w}}^{k + 1}},{b^{k + 1}}} \right)$,并将结果广播给物联网节点;(5) 物联网节点i根据服务器提供的参数$\left( {{{{w}}^{k + 1}},{b^{k + 1}}} \right)$对问题式(14)进行求解得到参数$\left( {{{w}}_i^{k + 1},b_i^{k + 1}} \right)$; (6) 物联网节点i根据式(17)和式(18)更新对偶变量$\left( {\gamma _{i,w}^{k + 1},\gamma _{i,b}^{k + 1}} \right)$; (7) 物联网节点i向服务器发送新的中间参数$\left( {{{w}}_i^{k + 1},b_i^{k + 1}} \right)$及$\left( {\gamma _{i,w}^{k + 1},\gamma _{i,b}^{k + 1}} \right)$; (8) $ k \leftarrow k + 1$; (9) until ${\left\| { {r^k} } \right\|_2} \le {\varepsilon ^{ {\rm{rel} } } }{\rm{,} }{\left\| { {s^k} } \right\|_2} \le {\varepsilon ^{ {\rm{abs} } } }$; /*算法达到收敛准则,停止迭代*/ -
BOYD S, PARIKH N, CHU E, et al. Distributed optimization and statistical learning via the alternating direction method of multipliers[J]. Foundations and Trends® in Machine Learning, 2011, 3(1): 1–122. doi: 10.1561/2200000016 邵振峰, 蔡家骏, 王中元, 等. 面向智能监控摄像头的监控视频大数据分析处理[J]. 电子与信息学报, 2017, 39(5): 1116–1122. doi: 10.11999/JEIT160712SHAO Zhenfeng, CAI Jiajun, WANG Zhongyuan, et al. Analytical processing method of big surveillance video data based on smart monitoring cameras[J]. Journal of Electronics &Information Technology, 2017, 39(5): 1116–1122. doi: 10.11999/JEIT160712 DHAR S, YI C R, RAMAKRISHNAN N, et al. ADMM based scalable machine learning on spark[C]. 2015 IEEE International Conference on Big Data (Big Data), Santa Clara, USA, 2015: 1174–1182. doi: 10.1109/BigData.2015.7363871. 赵海涛, 朱银阳, 丁仪, 等. 车联网中基于移动边缘计算的内容感知分类卸载算法研究[J]. 电子与信息学报, 2020, 42(1): 20–27. doi: 10.11999/JEIT190594ZHAO Haitao, ZHU Yinyang, DING Yi, et al. Research on content-aware classification offloading algorithm based on mobile edge calculation in the internet of vehicles[J]. Journal of Electronics &Information Technology, 2020, 42(1): 20–27. doi: 10.11999/JEIT190594 SHI Weisong, ZHANG Xingzhou, WANG Yifan, et al. Edge computing: State-of-the-art and future directions[J]. Journal of Computer Research and Development, 2019, 56(1): 69–89. doi: 10.7544/issn1000-1239.2019.20180760 CHOUDHURY T, GUPTA A, PRADHAN S, et al. Privacy and security of cloud-based Internet of Things (IoT)[C]. The 3rd International Conference on Computational Intelligence and Networks (CINE), Odisha, India, 2017: 40–45. doi: 10.1109/CINE.2017.28. ZOU Hui and HASTIE T. Regularization and variable selection via the elastic net[J]. Journal of the Royal Statistical Society: Series B (Statistical Methodology) , 2005, 67(2): 301–320. doi: 10.1111/j.1467-9868.2005.00503.x SHEN Yi, HAN Bing, and BRAVERMAN E. Stability of the elastic net estimator[J]. Journal of Complexity, 2016, 32(1): 20–39. doi: 10.1016/j.jco.2015.07.002 LUO Hezhi, SUN Xiaoling, and LI Duan. On the convergence of augmented lagrangian methods for constrained global optimization[J]. SIAM Journal on Optimization, 2007, 18(4): 1209–1230. doi: 10.1137/060667086 BERTSEKAS D P and TSITSIKLIS J N. Parallel and Distributed Computation: Numerical Methods[M]. London: Prentice Hall, 1989. ZHANG Yueqin, ZHENG Hao, and ZHANG Chuanlin. Global convergence of a modified PRP conjugate gradient method[J]. Procedia Engineering, 2012, 31: 986–995. doi: 10.1016/j.proeng.2012.01.1131 HE Bingsheng and YUAN Xiaoming. On the O(1/n) convergence rate of the Douglas-Rachford alternating direction method[J]. SIAM Journal on Numerical Analysis, 2012, 50(2): 700–709. doi: 10.1137/110836936 NISHIHARA R, LESSARD L, RECHT B, et al. A general analysis of the convergence of ADMM[C]. The 32nd International Conference on International Conference on Machine Learning, Lille, France, 2015: 343–352. EFRON B, HASTIE T, JOHNSTONE I, et al. Least angle regression[J]. Annals of Statistics, 2004, 32(2): 407–451. doi: 10.1214/009053604000000067 SPENCER B, ALFANDI O, and AL-OBEIDAT F. A refinement of lasso regression applied to temperature forecasting[J]. Procedia Computer Science, 2018, 130: 728–735. doi: 10.1016/j.procs.2018.04.127 -





 下载:
下载:







 下载:
下载:
