Light Field All-in-focus Image Fusion Based on Edge Enhanced Guided Filtering
-
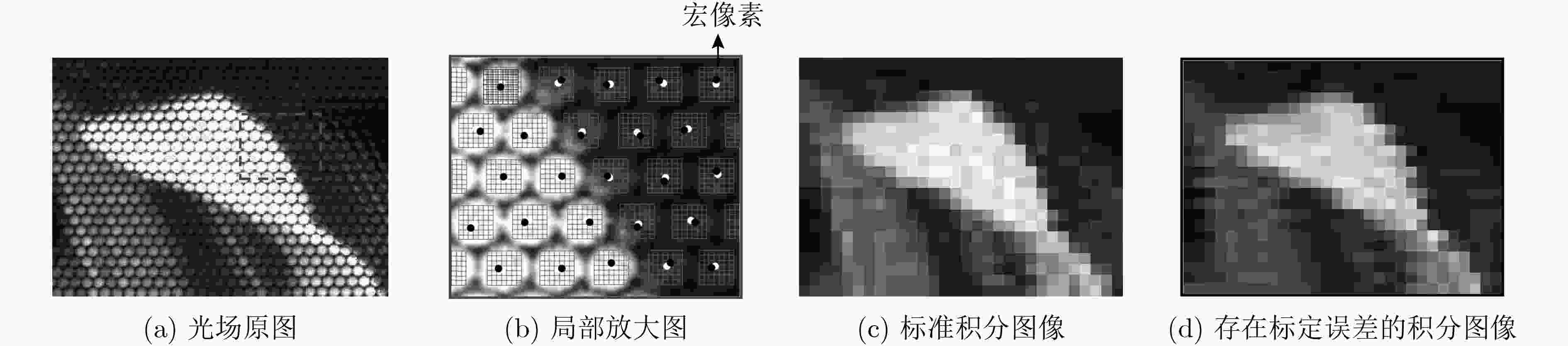
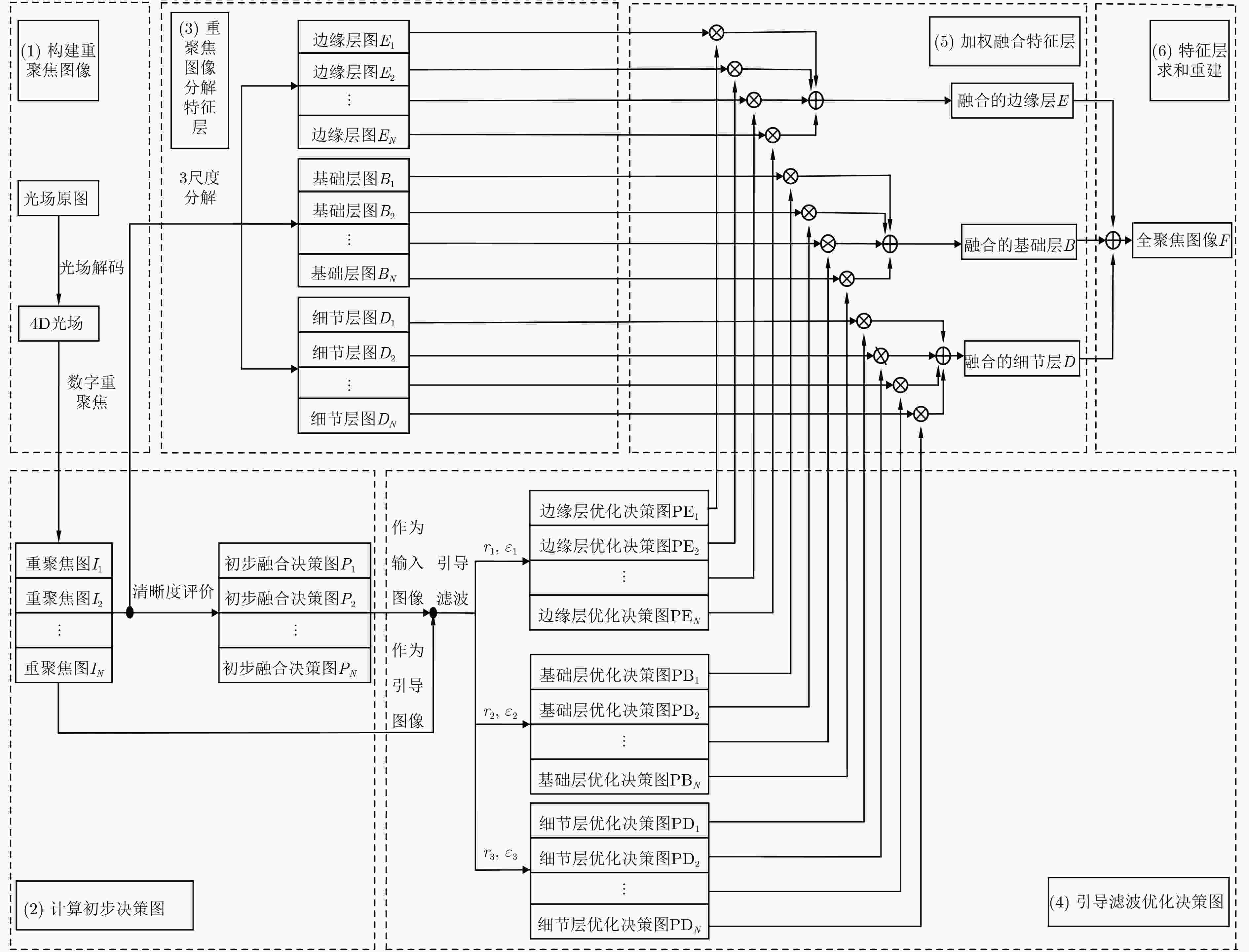
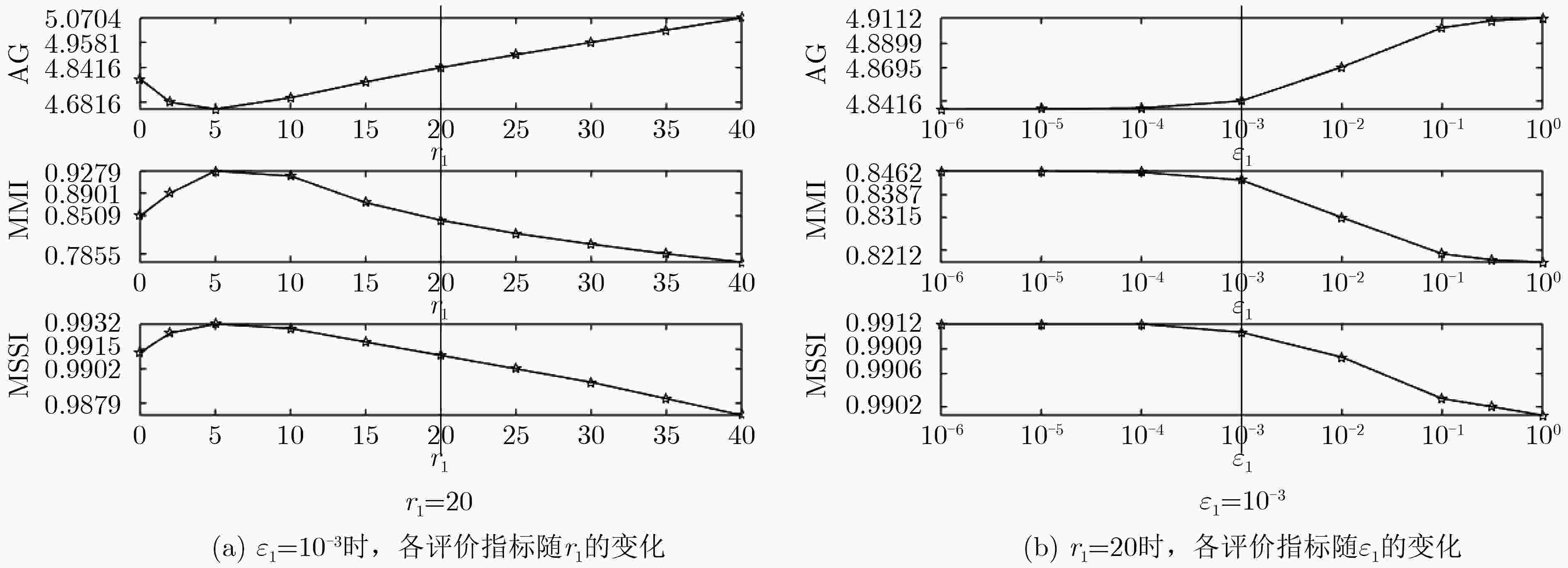
摘要: 受光场相机微透镜几何标定精度的影响,4D光场在角度方向上的解码误差会造成积分后的重聚焦图像边缘信息损失,从而降低全聚焦图像融合的精度。该文提出一种基于边缘增强引导滤波的光场全聚焦图像融合算法,通过对光场数字重聚焦得到的多幅重聚焦图像进行多尺度分解、特征层决策图引导滤波优化来获得最终全聚焦图像。与传统融合算法相比,该方法对4D光场标定误差带来的边缘信息损失进行了补偿,在重聚焦图像多尺度分解过程中增加了边缘层的提取来实现图像高频信息增强,并建立多尺度图像评价模型实现边缘层引导滤波参数优化,可获得更高质量的光场全聚焦图像。实验结果表明,在不明显降低融合图像与原始图像相似性的前提下,该方法可有效提高全聚焦图像的边缘强度和感知清晰度。Abstract: Affected by the micro-lens geometric calibration accuracy of the light field camera, the decoding error of the 4D light field in the angular direction will cause the edge information loss of the integrated refocused image, which will reduce the accuracy of the all-in-focus image fusion. In this paper, a light field all-in-focus image fusion algorithm based on edge-enhanced guided filtering is proposed. Through multi-scale decomposition of the digital refocused images and guided filtering optimization of the feature layer decision map, the final all-in-focus image is obtained. Compared with the traditional fusion algorithm, the edge information loss caused by the 4D light field calibration error is compensated in the presented method. In the step of multi-scale decomposition of the refocused image, the edge layer extraction is added to accomplish the high-frequency information enhancement. Then the multi-scale evaluation model is established to optimize the edge layer’s guided filtering parameters to obtain a better light field all-in-focus image. The experimental results show that the edge intensity and the perceptual sharpness of the all-in-focus image can be improved without significantly reducing the similarity between the all-in-focus image and the original image.
-
表 1 Flower图像不同融合算法性能评价指标比较
Flower IE EI FMI PSI PCA 7.7027 34.8908 0.6903 0.1806 WT 7.7178 39.4788 0.6343 0.1973 Laplace 7.6965 39.3516 0.7317 0.1867 BF 7.6929 39.0181 0.7521 0.1873 GFF 7.7081 38.6164 0.7333 0.1860 G-GRW 7.7047 38.8265 0.7435 0.1851 DSIFT 7.7054 39.4555 0.7494 0.1921 本文 7.7099 40.3353 0.6482 0.2330 表 2 Cup图像不同融合算法性能评价指标比较
Cup IE EI FMI PSI PCA 7.6366 39.7368 0.6145 0.1991 WT 7.6453 47.2613 0.5609 0.2768 Laplace 7.6172 46.1445 0.6891 0.2473 BF 7.6191 45.9757 0.6976 0.2478 GFF 7.6365 45.6423 0.6916 0.2400 G-GRW 7.6366 45.7279 0.6976 0.2467 DSIFT 7.6366 45.8104 0.6984 0.2474 本文 7.6366 47.2942 0.6392 0.2857 表 3 Runner图像不同融合算法性能评价指标比较
Runner IE EI FMI PSI PCA 7.4581 67.7672 0.7363 0.2844 WT 7.4673 76.1906 0.7286 0.3307 Laplace 7.4664 75.9168 0.7774 0.3260 BF 7.4606 74.4269 0.7834 0.3291 GFF 7.4653 74.4718 0.7835 0.3157 G-GRW 7.4654 74.4898 0.8285 0.3191 DSIFT 7.4664 74.9858 0.8293 0.3247 本文 7.4723 77.5482 0.7610 0.3497 -
LIU Yu, CHEN Xun, PENG Hu, et al. Multi-focus image fusion with a deep convolutional neural network[J]. Information Fusion, 2017, 36: 191–207. doi: 10.1016/j.inffus.2016.12.001 WU Gaochang, MASIA B, JARABO A, et al. Light field image processing: An overview[J]. IEEE Journal of Selected Topics in Signal Processing, 2017, 11(7): 926–954. doi: 10.1109/JSTSP.2017.2747126 GOSHTASBY A A and NIKOLOV S. Image fusion: Advances in the state of the art[J]. Information Fusion, 2007, 8(2): 114–118. doi: 10.1016/j.inffus.2006.04.001 刘帆, 裴晓鹏, 张静, 等. 基于优化字典学习的遥感图像融合方法[J]. 电子与信息学报, 2018, 40(12): 2804–2811. doi: 10.11999/JEIT180263LIU Fan, PEI Xiaopeng, ZHANG Jing, et al. Remote sensing image fusion based on optimized dictionary learning[J]. Journal of Electronics &Information Technology, 2018, 40(12): 2804–2811. doi: 10.11999/JEIT180263 谢颖贤, 武迎春, 王玉梅, 等. 基于小波域清晰度评价的光场全聚焦图像融合[J]. 北京航空航天大学学报, 2019, 45(9): 1848–1854. doi: 10.13700/j.bh.1001-5965.2018.0739XIE Yingxian, WU Yingchun, WANG Yumei, et al. Light field all-in-focus image fusion based on wavelet domain sharpness evaluation[J]. Journal of Beijing University of Aeronautics and Astronautics, 2019, 45(9): 1848–1854. doi: 10.13700/j.bh.1001-5965.2018.0739 肖斌, 唐翰, 徐韵秋, 等. 基于Hess矩阵的多聚焦图像融合方法[J]. 电子与信息学报, 2018, 40(2): 255–263. doi: 10.11999/JEIT170497XIAO Bin, TANG Han, XU Yunqiu, et al. Multi-focus image fusion based on Hess matrix[J]. Journal of Electronics &Information Technology, 2018, 40(2): 255–263. doi: 10.11999/JEIT170497 ZHANG Yu, BAI Xiangzhi, and WANG Tao. Boundary finding based multi-focus image fusion through multi-scale morphological focus-measure[J]. Information Fusion, 2017, 35: 81–101. doi: 10.1016/j.inffus.2016.09.006 SUN Jianguo, HAN Qilong, KOU Liang, et al. Multi-focus image fusion algorithm based on Laplacian pyramids[J]. Journal of the Optical Society of America A, 2018, 35(3): 480–490. doi: 10.1364/JOSAA.35.000480 WAN Tao, ZHU Chenchen, and QIN Zengchang. Multifocus image fusion based on robust principal component analysis[J]. Pattern Recognition Letters, 2013, 34(9): 1001–1008. doi: 10.1016/j.patrec.2013.03.003 LIU Yu, LIU Shuping, and WANG Zengfu. Multi-focus image fusion with dense SIFT[J]. Information Fusion, 2015, 23: 139–155. doi: 10.1016/j.inffus.2014.05.004 LI Shutao, KANG Xudong, and HU Jianwen. Image fusion with guided filtering[J]. IEEE Transactions on Image Processing, 2013, 22(7): 2864–2875. doi: 10.1109/TIP.2013.2244222 MA Jinlei, ZHOU Zhiqiang, WANG Bo, et al. Multi-focus image fusion based on multi-scale focus measures and generalized random walk[C]. The 36th Chinese Control Conference, Dalian, China, 2017: 5464–5468. doi: 10.23919/ChiCC.2017.8028223. NG R, LEVOY M, BREDIF M, et al. Light field photography with a hand-held plenoptic camera[R]. Stanford Tech Report CTSR 2005-02, 2005. SOTAK JR G E and BOYER K L. The laplacian-of-gaussian kernel: A formal analysis and design procedure for fast, accurate convolution and full-frame output[J]. Computer Vision, Graphics, and Image Processing, 1989, 48(2): 147–189. doi: 10.1016/s0734-189x(89)80036-2 HE Kaiming, SUN Jian, and TANG Xiaoou. Guided image filtering[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2013, 35(6): 1397–1409. doi: 10.1109/TPAMI.2012.213 YOON Y, JEON H G, YOO D, et al. Light-field image super-resolution using convolutional neural network[J]. IEEE Signal Processing Letters, 2017, 24(6): 848–852. doi: 10.1109/LSP.2017.2669333 SCHMIDT M, LE ROUX N, and BACH F. Minimizing finite sums with the stochastic average gradient[J]. Mathematical Programming, 2017, 162(1/2): 83–112. doi: 10.1007/s10107-016-1030-6 LIU Zheng, BLASCH E, XUE Zhiyun, et al. Objective assessment of multiresolution image fusion algorithms for context enhancement in night vision: A comparative study[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2012, 34(1): 94–109. doi: 10.1109/tpami.2011.109 JUNEJA M and SANDHU P S. Performance evaluation of edge detection techniques for images in spatial domain[J]. International Journal of Computer Theory and Engineering, 2009, 1(5): 614–621. doi: 10.7763/IJCTE.2009.V1.100 HAGHIGHAT M and RAZIAN M A. Fast-FMI: Non-reference image fusion metric[C]. The 8th IEEE International Conference on Application of Information and Communication Technologies, Astana, Kazakhstan, 2014: 1–3. doi: 10.1109/ICAICT.2014.7036000. FEICHTENHOFER C, FASSOLD H, and SCHALLAUER P. A perceptual image sharpness metric based on local edge gradient analysis[J]. IEEE Signal Processing Letters, 2013, 20(4): 379–382. doi: 10.1109/LSP.2013.2248711 -






 下载:
下载:








 下载:
下载:
