Study on the Characteristics of Composite Electromagnetic Scattering From Soil Surface and Combinatorial Target Placed on It
-
摘要: 为了满足置于粗糙面之上组合目标测量和检测的需要，该文分别采用Dobson半经验模型和电介质复介电常数公式表示土壤介电常数的实部和虚部，应用指数型分布粗糙面和Monte Carlo方法模拟实际的土壤表面。通过与矩量法得到的计算结果比较，验证了时域有限差分(FDTD)方法计算粗糙面与目标复合散射问题的有效性，进而运用该方法研究了土壤表面与置于其上组合目标的复合散射，得出了复合散射系数的角分布曲线。结果表明：复合散射系数随散射角振荡地变化，在镜反射方向处发生散射增强效应；土壤表面高度起伏均方根越大，复合散射系数越大；相关长度越大，复合散射系数越小；湿度越大，复合散射系数越小；组合目标尺度、介电常数、入射角对复合散射系数影响比较复杂。该文结果可用于求解地、海粗糙面与置于其上任意目标的复合电磁散射问题，与其它数值计算方法相比较，采用时域有限差分方法既可获得较高的准确性，同时又可减少计算时间和内存占用量。Abstract: In order to meet the needs of measuring and detecting combinatorial target placed on the rough surface, Dobson semi-empirical model and dielectric complex permittivity formula are used to represent the real and imaginary parts of the soil dielectric constant, the soil surface is simulated with the model of exponential distribution and Monte Carlo method. The strategy of the Finite Difference Time Domain (FDTD) method for calculating the composite scattering from rough surface with target and the modeling method are presented with their validity evaluated by the method of moment, then the composite scattering of soil surface and combinatorial target placed on it is studied by this method, the angular distribution curve of the composite scattering coefficient is obtained. The results show that the composite scattering coefficient oscillates with the scattering angle, and the scattering enhancement effect occurs in the mirror reflection direction; the larger the root mean square of the fluctuation of soil surface, the larger the composite scattering coefficient; the larger the correlation length, the smaller the composite scattering coefficient; the larger the soil moisture content, the smaller the composite scattering coefficient; the influence of the scale and dielectric constant of combinatorial target, incident angle on composite scattering coefficient is complex. The results obtained in this paper can be used to solve the composite electromagnetic scattering from rough land surface and rough sea surface with any target placed on it. Compared with other numerical methods, the finite difference time domain method can not only obtain higher accuracy, but also reduce the calculation time and the amount of memory occupying.
-
1. 引言
地海背景与目标的复合电磁散射研究在军用目标探测、识别以及民用遥感等领域有着广泛的应用。如陆地、海洋表面上方目标监测、低飞目标识别与制导截获技术；半埋目标识别；下方埋藏目标探测；陆地表面静止或运动战车、海洋表面漂浮或运动舰船监测等诸多理论和工程问题都需要对地、海背景与目标的复合散射问题进行研究，开展地、海背景与目标复合散射特性研究，可为目标回波特性的数据采集、特征提取、控制和识别、精确制导、仿真以及隐身与反隐身技术的深入研究提供必要的理论依据和实用模型[1-4]。
在以往的粗糙面与目标复合散射特性研究中，研究海洋表面与目标复合散射很多[5-10]，而研究地物表面与邻近目标复合散射则较少[11,12]。实际上，地球表面总面积约5.1×104 km2，其中海洋面积3.61×104 km2，陆地面积1.49×104 km2，海洋占地球表面积的71%，陆地占地球表面积的29%，可以说七分海洋三分陆地。因此，研究地物表面与目标复合散射特性与研究海洋表面与目标复合散射特性具有同等重要的意义。在粗糙地物表面与邻近目标复合散射特性的研究中，以往主要是研究粗糙地面与上方、半埋、埋藏目标的复合散射[13,14]，鲜有数值计算粗糙地面与置于其上目标复合模型散射特性的报道。事实上，地物表面上静止陆军装备，如坦克、装甲车辆；空军装备，如战斗机、轰炸机；航天装备，如卫星、火箭；民用火车、汽车、飞机等等，当它们停放在陆地表面并处于雷达监测范围内时，均属于粗糙地物表面与置于其上目标的复合模型。
本文采用Dobson半经验模型[15,16]和电介质复介电常数公式[17,18]表示土壤介电常数的实部和虚部，应用指数型分布粗糙面[19]和Monte Carlo方法[20]模拟土壤表面，运用时域有限差分(FDTD)方法[21]研究了时谐电磁波入射条件下土壤表面与置于其上组合目标的复合电磁散射特性。
2. 复合散射模型建立
图1为土壤表面与组合目标复合散射几何示意图，土壤表面上方为自由空间，下方为无限延伸的各向同性均匀土壤介质，组合目标由等腰梯形、长方形和等腰三角形组合而成，
h1 ,h2 ,h3 分别表示等腰梯形、长方形和等腰三角形的高，d1 为梯形底边半宽度，d2 为三角形底边半宽度。图2为土壤表面与组合目标复合散射计算的FDTD模型，其中连接边界AB取为平面并延伸至吸收边界层，连接边界AB下方为总场区，上方为散射场区，入射波通过在连接边界上设置等效电磁流引入总场区，在散射场区设置输出边界CD，输出边界与连接边界平行并延伸至吸收层，在FDTD计算区域外部设置UPML吸收边界，厚度取10个网格。在交变电磁场下，电介质的复介电常数可以表示为
ε=ε′−jε″ (1) 其中，
{\rm{j}} 为虚数单位，\varepsilon ' 和\varepsilon '' 分别表示介电常数的实部和虚部，{\varepsilon ''_{\rm{r}}} 与介质电导率\sigma 的关系为\varepsilon '' = {\sigma / {{\varepsilon _0}\omega }} ,\omega 为电磁波角频率。土壤是由空气、水分和固相物质组成的混合物，目前常用的土壤介电模型可分为理论模型、半经验模型和经验模型，在遥感领域应用比较多的0.3～100 GHz微波波段中，其中的半经验模型被广泛应用。目前，比较典型的半经验模型主要有Wang模型、Dobson模型和普适折射指数混合介电模型[15-18]，对于Dobson模型而言，它是在1.4～18 GHz的实测数据发展起来的，虽然适用频率范围较小，精度也受到一定的限制，但是只需输入土壤容重、土壤质地、含水量等简单参数就可以算出土壤的介电常数，应用比较方便，因此被广泛应用。
土壤介电常数实部的Dobson半经验模型[15,16](Dobson semi empirical model)表达式为
{\varepsilon '_{\rm{r}}} = \left[1 + \frac{{{\rho _{\rm{b}}}}}{{{\rho _{\rm{s}}}}}(\varepsilon _{\rm{s}}^\alpha - 1) + m_{\rm{v}}^\beta \varepsilon _{{\rm{fw}}}^{' \alpha } - {m_{\rm{v}}})\right]{^{\frac{1}{\alpha }}} (2) 其中，
{\rho _{\rm{b}}} 表示单位体积土壤的质量({\rm{g}} \cdot {\rm{c}}{{\rm{m}}^{ - 3}} ),{\rho _{\rm{s}}} 表示土壤中固态物质密度，不同类型土壤固态物质密度差别不大，一般取{\rho _{\rm{s}}} = 2.66\;{\rm{g}} \cdot {\rm{c}}{{\rm{m}}^{ - 3}} ,{\varepsilon _{\rm{s}}} 为固态物质介电常数，一般取{\varepsilon _{\rm{s}}} = 4.7 ,\alpha 为一常数因子，对所有土壤的最优值为0.65,{m_{\rm{v}}} 是土壤体积比湿度，\beta 是一可调参数，与土壤类型有关，{\varepsilon '_{{\rm{fw}}}} 表示自由水介电常数实部。{\rho _{\rm{b}}} 可以用经验式(3)进行计算{\rho _{\rm{b}}} = {{3.4355} / {{r^{0.3018}}}} (3) 其中，
r 可按式(4)计算r = 25.1 - 0.21{f_{\rm{s}}} + 0.22{f_{\rm{c}}} (4) 其中，
{f_{\rm{s}}} 和{f_{\rm{c}}} 表示土壤中沙和黏土所占的比例，如果土壤为沙性黏土，沙占30.6%，淤泥占55.9%，黏土占13.5%，因此，本文计算中{f_{\rm{s}}} ,{f_{\rm{c}}} 分别取为30.6%, 13.5%。参数
\beta 的经验表达式为\beta = 1.09 - 0.11{f_{\rm{s}}} + 0.18{f_{\rm{c}}} (5) 自由水介电常数实部
{\varepsilon '_{{\rm{fw}}}} 可按纯水介电常数模型进行计算。Debye方程描述了纯水复介电常数与频率f 的关系，自由水介电常数的实部{\varepsilon '_{{\rm{fw}}}} 为{\varepsilon '_{{\rm{fw}}}} = {\varepsilon _{{\rm{w}}\infty }} + \frac{{{\varepsilon _{{\rm{w}}0}} - {\varepsilon _{{\rm{w}}\infty }}}}{{1 + {{(2\pi f{\tau _{\rm{w}}})}^2}}} (6) 其中，
{\varepsilon _{{\rm{w}}\infty }} = 4.9 是高频(或光学)介电常数，由实验确定，张弛时间{\tau _{\rm{w}}} 与温度T (单位℃)的关系为\begin{split} 2\pi {\tau _{\rm{w}}}(T) =\,& 1.1109 \times {10^{ - 10}} - 3.824 \times {10^{ - 12}}T \\ & + 6.938 \times {10^{ - 14}}{T^2} - 5.096 \times {10^{ - 16}}{T^3} \end{split} (7) 其中，
{\varepsilon _{{\rm{w}}0}} 是静态介电常数，与温度的关系为\begin{split} {\varepsilon _{{\rm{w}}0}} =\,& 187.134 - 1.949 \times {10^{ - 1}}T - 1.276 \times {10^{ - 2}}{T^2} \\ & + 2.491 \times {10^{ - 4}}{T^3}\\[-10pt] \end{split} (8) 土壤介电常数的虚部为
{\varepsilon ''_{\rm{r}}} = \frac{\sigma }{\omega } (9) 近年来土壤学研究表明，土壤电导率
\sigma 与土壤性质密切相关，土壤中盐分、水分及有机质含量，土壤压实度、质地结构和孔隙率等都不同程度地影响着土壤电导率，其取值范围为1.4×10–4～ 5×10–2 s·m–1，在土壤温度为T = 298\;{\rm{K}} 时，土壤电导率\sigma 为2.32 \times {10^{ - 2}}\;\rm s \cdot {m^{ - 1}} 。土壤表面高度起伏遵守指数谱分布规律，指数谱分布的功率谱密度为[12]
S(k) = \frac{{{\delta ^2}l}}{{\pi (1 + {k^2}{l^2})}}{\rm{ }} (10) 其中，
\delta ,l 分别为土壤表面高度起伏均方根、相关长度，k 为波数。3. FDTD方法
根据时域有限差分(FDTD)方法理论[21]，电磁场2维问题TM波差分方程可表示为
\begin{split} &H_x^{n + 1/2}\left( {i,j + 1/2} \right) \\ & \quad = {\rm{CP}}\left( m \right)H_x^{n - 1/2}\left( {i,j + 1/2} \right) \\ & \qquad - {\rm{CQ}}\left( m \right)\frac{{E_z^n\left( {i,j + 1} \right) - E_z^n\left( {i,j} \right)}}{{\Delta y}}\hspace{20pt} \end{split} (11) \begin{split} &H_y^{n + 1/2}\left( {i + 1/2,j} \right) \\ & \quad = {\rm{CP}}\left( m \right)H_y^{n - 1/2}\left( {i + 1/2,j} \right) \\ & \qquad + {\rm{CQ}}\left( m \right)\frac{{E_z^n\left( {i + 1,j} \right) - E_z^n\left( {i,j} \right)}}{{\Delta x}}\hspace{20pt} \end{split} (12) \begin{split} &E_z^{n + 1}(i,j) \\ & \quad = {\rm{CA}}(m)E_z^n(i,j) + {\rm{CB}}(m) \\ &\qquad \cdot\left[ \frac{{H_y^{n + 1/2}(i + 1/2,j) - H_y^{n + 1/2}(i - 1/2,j)}}{{\Delta x}}\right. \\ &\qquad \left.- \frac{{H_x^{n + 1/2}(i,j + 1/2) - H_x^{n + 1/2}(i,j - 1/2)}}{{\Delta y}} \right]\\ \end{split} (13) 其中，
m 为方程左边场分量FDTD网格节点位置。\Delta x ,\Delta y 分别为FDTD区域x ,y 方向的离散网格宽度。吸收边界采用各向异性介质完全匹配层(UPML)实现。以TM波为例，各向异性介质Maxwell旋度方程(无源)为
\frac{{\partial {E_z}}}{{\partial y}} = - {\rm j}\omega {\mu _1}\frac{{{s_y}}}{{{s_x}}}{H_x} \hspace{60pt} (14) \frac{{\partial {E_z}}}{{\partial x}} = {\rm j}\omega {\mu _1}\frac{{{s_x}}}{{{s_y}}}{H_y}\hspace{70pt} (15) \frac{{\partial {H_y}}}{{\partial x}} - \frac{{\partial {H_x}}}{{\partial y}} = ({\rm j}\omega {\varepsilon _1} + {\sigma _1}){s_x}{s_y}{E_z} (16) 其中，
{\varepsilon _1} ,{\mu _1} ,{\sigma _1} 表示计算域内部介质介电参数。{s_x} 和{s_y} 分别为x 和y 方向的单轴参数，可分别表示为{s_x} = {\kappa _x} - {\sigma _x}/{\rm{j}}\omega {\varepsilon _0},\;{s_y} = {\kappa _y} - {\sigma _y}/{\rm{j}}\omega {\varepsilon _0} (17) 其中，
{\sigma _x} ,{\kappa _x} 分别为\left. \begin{aligned} {\sigma _x}\left( x \right) \,& = {\sigma _{\max }}{{({{\left| {x - {x_0}} \right|}^n})} / {{d^n}}},\; \\ {\kappa _x}\left( x \right)&= 1 + ({\kappa _{\max }} - 1){{({{\left| {x - {x_0}} \right|}^n})} / {{d^n}}} \end{aligned}\right\} (18) 其中，
d 为UPML层厚度，根据文献[21]，取n = 4 ,{\sigma _{\max }} = {{(n + 1)} / {(\sqrt {{\varepsilon _{\rm{r}}}} 150\pi \delta )}} ,{\kappa _{\max }} = 5 \sim 11 ，吸收效果较佳。FDTD计算达到稳定后，记录输出边界上近场计算结果，根据等效原理利用时谐场外推法可以得到远区散射场。土壤表面与置于其上组合目标复合散射系数为
{\sigma _{\rm{s}}} = 10\lg ({\rm{NRCS}})\;{\rm{dB}} (19) 式(19)中归一化雷达散射截面
{\rm{NRCS}} 具体形式为{\rm{NRCS}} = \mathop {\lim }\limits_{r \to \infty } \frac{{2\pi r}}{L}\frac{{{{\left| {{E_{\rm{s}}}} \right|}^2}}}{{{{\left| {{E_{\rm{i}}}} \right|}^2}}} (20) 其中，
r ,{E_{\rm{s}}} 和{E_{\rm{i}}} 分别表示观察点到原点的距离、远区散射场、入射波电场，L 为土壤表面取样长度。4. 算法验证及误差分析
为了验证本文FDTD算法的有效性，用时谐场FDTD计算了指数型粗糙面与上方无限长导体圆柱目标的复合散射系数，并与MOM计算结果进行了比较，如图3所示。计算中，入射波频率
f = 0.3\;{\rm{GHz}} ，入射角{\theta _i} = {60^ \circ } ，粗糙面高度起伏均方根\delta = 0.2\lambda ，相关长度l = 1.5\lambda ，粗糙面相对复介电常数为{\varepsilon _{\rm{r}}} = 2.5 - {\rm{j}}0.18 ，无限长导体圆柱横截面半径r = \lambda ，其中心到粗糙面的距离{h_{\rm{t}}} = 3.0\lambda 。由图3可以看出两种算法得到的复合散射系数角分布曲线吻合较好，结果基本一致，这样就验证了本文算法的有效性。此外，还可以通过误差分析对本文算法有效性进行验证，将时域有限差分方法计算结果与矩量法进行对比。两者之间的绝对误差可以表示为
\varDelta = \left| {{\sigma ^{{\rm{FDTD}}}} - {\sigma ^{{\rm{MoM}}}}} \right|({\rm{dB}}) (21) 单独采用绝对误差并不能很好地说明两者之间的误差，这里，通过求解其相对误差以便能够做更好的对比，FDTD和MoM复合散射系数的相对误差可以由式(22)得到
\varDelta = \sum {\left| {{\sigma ^{{\rm{FDTD}}}} - {\sigma ^{{\rm{MoM}}}}} \right|} \Bigr/\sum \left| {{\sigma ^{{\rm{MoM}}}}} \right| \times 100\% (22) 为了比较两者之间的误差，图4给出了图3中FDTD与MoM计算结果的绝对误差，与MoM对比，FDTD与其存在的平均误差为1.0394 dB，相对误差约为4.8726%。这说明FDTD方法可以正确地用以分析土壤表面与置于其上目标的复合散射问题。
5. 数值仿真与结果分析
理论和实践均表明，土壤介电常数对复合散射特性的影响是比较大的，当土壤介电常数的实部采用Dobson模型时，它随土壤湿度变化关系如图5所示。
从图5可以看出，不管沙土含量
{f_{\rm{s}}} 、黏土含量{f_{\rm{c}}} 如何取值，土壤介电常数实部均随湿度的增大呈非线性增大，并且{f_{\rm{s}}} 越大，增大得越快。在以下的数值仿真中，如没有进行特别说明，入射电磁波的频率取为
{\rm{0}}{\rm{.3}}\;{\rm{GHz}} ，入射角{\theta _{\rm{i}}} = {20^ \circ } ，土壤介电常数的实部采用Dobson模型式(2)进行计算，虚部采用式(9)进行计算。FDTD空间网格宽度\varDelta = {\lambda / {20}} ，时间网格宽度\Delta t = {\varDelta / {2{\rm{c}}}} ,{\rm{c}} 为真空中光速。土壤表面高低起伏满足指数谱分布规律，取样长度L = 3600\varDelta ，统计个数为20个。组合目标几何参数{h_1} = 3.0\lambda ,{h_2} = 6.0\lambda ,{h_3} = 1.0\lambda ,{d_1} = 2.0\lambda ,{d_2} = 1.0\lambda 。5.1 土壤表面粗糙度参数对复合散射系数的影响
图6为复合散射系数
{\sigma _{\rm{s}}} 随土壤表面高度起伏均方根\delta 的变化关系。计算中取土壤表面相关长度l = 1.5\lambda ，土壤介电常数{\varepsilon _{{\rm{soil}}}} = 7.28 - {\rm{j}}0.27 ，目标介电常数{\varepsilon _{\rm{t}}} = 2.4 。从图6可以看出，复合散射系数{\sigma _{\rm{s}}} 随散射角{\theta _{\rm{s}}} 振荡地变化，在镜反射方向附近({\theta _{\rm{s}}} = {20^ \circ } )复合散射系数显著地增大并在镜反射方向处达到最大，存在散射增强效应，在镜向附近{\sigma _{\rm{s}}} 随土壤表面均方根\delta 的增大而减小，在其它散射方向，\delta 越大，{\sigma _{\rm{s}}} 越大，角分布曲线振荡的幅度越小，即土壤表面均方根越大，复合散射系数就越大，角分布曲线振荡的幅度越小。在土壤表面相关长度一定的情况下，土壤表面高度起伏均方根越大，则土壤表面的粗糙度就越大，镜向方向散射减弱，其它方向散射增强，散射效应增强，所以复合散射系数就越大。
图7为复合散射系数
{\sigma _{\rm{s}}} 随土壤表面相关长度l 的变化关系。计算时取\delta = 0.15\lambda ，土壤介电常数{\varepsilon _{{\rm{soil}}}} = 7.28 - {\rm{j}}0.27 ，目标介电常数{\varepsilon _{\rm{t}}} = 2.4 。由图7可以看出，复合散射系数{\sigma _{\rm{s}}} 随散射角{\theta _{\rm{s}}} 振荡地变化(以下不再赘述)，在镜反射方向附近({\theta _{\rm{s}}} = {20^ \circ } )复合散射系数显著地增大并在镜反射方向处达到最大，存在散射增强效应(以下不再赘述)，在镜向附近相关长度l 对{\sigma _{\rm{s}}} 的影响较大，但影响规律较为复杂，在其它散射方向，l 越大，{\sigma _{\rm{s}}} 越小，角分布曲线振荡的幅度越大，即土壤表面相关长度越大，角分布曲线振荡的幅度越大。在土壤表面均方根一定的情况下，土壤表面相关长度越大，则土壤表面的粗糙度就越小，散射效应减弱，所以复合散射系数就越小。
5.2 土壤湿度对复合散射系数的影响
图8为复合散射系数
{\sigma _{\rm{s}}} 随土壤湿度{m_{\rm{v}}} 的变化关系。计算时取\delta = 0.15\lambda ,l = 1.5\lambda ，目标介电常数{\varepsilon _{\rm{t}}} = 2.4 。经计算，土壤介电常数虚部对复合散射系数几乎没有影响，而Dobson模型中湿度影响土壤介电常数的实部，所以本算例计算了土壤湿度对复合散射系数的影响。从图8可以看出，土壤湿度{m_{\rm{v}}} 对复合散射系数{\sigma _{\rm{s}}} 的影响亦较大，在散射角变化的大部分范围内，{m_{\rm{v}}} 越大，{\sigma _{\rm{s}}} 越大，角分布曲线振荡的幅度越小，即土壤湿度越大，复合散射系数就越大，角分布曲线振荡的幅度越小。在其它参数不变的情况下，土壤湿度越大，土壤的介电常数的实部就越大，透射到下方介质的能量越小，散射到上方介质的能量越大，所以复合散射系数就越大。
5.3 组合目标尺度对复合散射系数的影响
图9为复合散射系数
{\sigma _{\rm{s}}} 随目标尺度{k_{\rm{s}}} 的变化关系。计算时取\delta = 0.1\lambda ,l = 1.5\lambda ，土壤介电常数{\varepsilon _{{\rm{soil}}}} = 4.98 - {\rm{j}}0.15 ，目标介电常数{\varepsilon _{\rm{t}}} = 2.4 。从图9可以看出，组合目标尺度{k_{\rm{s}}} 对复合散射系数{\sigma _{\rm{s}}} 的影响比较复杂，当散射角{\theta _{\rm{s}}} < - {20^\circ } 时，组合目标尺度越大，{\sigma _{\rm{s}}} 越大，当散射角{\theta _{\rm{s}}} > - {20^\circ} 时，组合目标尺度对复合散射系数几乎没有影响。在其它参数不变的条件下，当
{\theta _{\rm{s}}} < - {20^\circ} 时，组合目标尺度越大，目标表面散射以及目标与土壤表面的耦合散射作用越强，所以散射系数越大。5.4 目标介电常数对复合散射系数的影响
图10为复合散射系数
{\sigma _{\rm{s}}} 随组合目标介电常数{\varepsilon _{\rm{t}}} 的变化关系。图10中，\delta = 0.15\lambda ,l = 1.5\lambda ，土壤介电常数{\varepsilon _{{\rm{soil}}}} = 7.28 - {\rm{j}}0.27 。由图10可以看出，组合目标介电常数对复合散射系数的影响比较复杂，当散射角{\theta _{\rm{s}}} < - {20^\circ} 时，组合目标介电常数越大，{\sigma _{\rm{s}}} 越大，当组合目标为金属导体时，{\sigma _{\rm{s}}} 最大，当散射角{\theta _{\rm{s}}} > - {20^\circ} 时，组合目标介电常数对复合散射系数几乎没有影响。在其它参数不变的条件下，当
{\theta _{\rm{s}}} < - {20^\circ} 时，组合目标介电常数越大，组合目标对电磁波吸收作用减小、散射作用增强，所以散射系数越大。5.5 入射角对复合散射系数的影响
图11为复合散射系数
{\sigma _{\rm{s}}} 随入射角{\theta _{\rm{i}}} 的变化关系。计算时，\delta = 0.15\lambda ,l = 1.5\lambda ，土壤介电常数{\varepsilon _{{\rm{soil}}}} = 7.28 - {\rm{j}}0.27 ，目标介电常数{\varepsilon _{\rm{t}}} = 2.4 。由图11可以看出，随着入射角的变化，曲线的最大值位置发生了变化，入射角对复合散射系数的影响是非常复杂的。当{\theta _{\rm{s}}} < - {50^\circ} 时，{\theta _{\rm{i}}} 对{\sigma _{\rm{s}}} 几乎没有影响；当- {50^\circ} < {\theta _{\rm{s}}} < {15^\circ} 时，{\theta _{\rm{i}}} 越大，{\sigma _{\rm{s}}} 越小；当{15^\circ} < {\theta _{\rm{s}}} < {40^\circ} 时，{\theta _{\rm{i}}} 对{\sigma _{\rm{s}}} 影响比较复杂，并无固定的规律可循；当{\theta _{\rm{s}}} > {40^\circ} ,{\theta _{\rm{i}}} 越大，{\sigma _{\rm{s}}} 越大。6. 结束语
本文运用时域有限差分方法研究了土壤表面与置于其上组合目标复合模型的电磁散射问题，得出了复合散射系数的角分布曲线，分析了复合散射系数随土壤表面高度起伏均方根、相关长度、土壤湿度、组合目标尺度、介电常数、入射角等参数的变化规律。结果表明，复合散射系数随散射角振荡地变化，在镜反射方向处发生散射增强效应；土壤表面高度起伏均方根越大，复合散射系数越大；相关长度越大，复合散射系数越小；湿度越大，复合散射系数越大；组合目标尺度、介电常数、入射角对复合散射系数影响比较复杂。本文计算结果对粗糙地物表面与目标复合电磁散射特性的认识以及复杂环境中目标的识别具有一定的应用价值。
-
TSANG L, LIAO T, TAN Shurun, et al. Rough surface and volume scattering of soil surfaces, ocean surfaces, snow, and vegetation based on numerical maxwell model of 3-D simulations[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2017, 10(11): 4703–4720. doi: 10.1109/JSTARS.2017.2722983 KIM S B, VAN ZYL J J, JOHNSON J T, et al. Surface soil moisture retrieval using the L-Band synthetic aperture radar onboard the soil moisture active-passive satellite and evaluation at core validation sites[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(4): 1897–1914. doi: 10.1109/TGRS.2016.2631126 KHANKHOJE U K and PADHY S. Stochastic solutions to rough surface scattering using the finite element method[J]. IEEE Transactions on Antennas and Propagation, 2017, 65(8): 4170–4180. doi: 10.1109/TAP.2017.2715366 CHANG Wenmo, DING K H, TSANG L, et al. Microwave scattering and medium characterization for terrestrial snow with QCA-Mie and bicontinuous models: Comparison studies[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(6): 3637–3648. doi: 10.1109/TGRS.2016.2522438 ALTUNCU Y. A numerical method for electromagnetic scattering by 3-D dielectric objects buried under 2-D locally rough surfaces[J]. IEEE Transactions on Antennas and Propagation, 2015, 63(8): 3634–3643. doi: 10.1109/TAP.2015.2438859 BELLEZ S, BOURLIER C, and KUBICKÉ G. 3-D scattering from a PEC target buried beneath a dielectric rough surface: An efficient PILE-ACA algorithm for solving a hybrid KA-EFIE formulation[J]. IEEE Transactions on Antennas and Propagation, 2015, 63(11): 5003–5014. doi: 10.1109/TAP.2015.2480123 XU Runwen, GUO Lixin, HE Hongjie, et al. A hybrid FEM/MoM technique for 3-D electromagnetic scattering from a dielectric object above a conductive rough surface[J]. IEEE Geoscience and Remote Sensing Letters, 2016, 13(3): 314–318. doi: 10.1109/LGRS.2015.2508500 SUN Hualong, TONG Chuangming, and ZOU Gaoxiang. High efficiency iterative solver for modeling composite rough surface electromagnetic scattering[J]. Electromagnetics, 2017, 37(2): 113–126. doi: 10.1080/02726343.2017.1279113 苏翔, 吴振森, 王晓冰, 等. 稀疏矩阵规范网格结合物理双网格分析介质海面散射特性与试验验证[J]. 电子与信息学报, 2016, 38(2): 486–494. doi: 10.11999/JEIT150401SU Xiang, WU Zhensen, WANG Xiaobing, et al. Backscatter analysis of lossy dielectric sea surface using SMCG-PBTG method—comparison with experimental data[J]. Journal of Electronics &Information Technology, 2016, 38(2): 486–494. doi: 10.11999/JEIT150401 王童, 童创明, 李西敏, 等. 海洋粗糙面全极化电磁散射特性研究[J]. 电子与信息学报, 2018, 40(6): 1412–1418. doi: 10.11999/JEIT170924WANG Tong, TONG Chuangming, LI Ximin, et al. Research on the full polarimetric electromagnetic scattering characteristics of ocean rough surface[J]. Journal of Electronics &Information Technology, 2018, 40(6): 1412–1418. doi: 10.11999/JEIT170924 REN Xincheng, ZHAO Ye, YANG Pengju, et al. Electromagnetic scattering by multiple columns partially buried in a ground plane[J]. International Journal of Antennas and Propagation, 2017, 2017: 8101509. doi: 10.1155/2017/8101509 任新成, 朱小敏, 刘鹏. 大地土壤表面与浅埋多目标宽带复合电磁散射研究[J]. 物理学报, 2016, 65(20): 204101. doi: 10.7498/aps.65.204101REN Xincheng, ZHU Xiaomin, and LIU Peng. Wide-band composite electromagnetic scattering from the earth soil surface and multiple targets shallowly buried[J]. Acta Physica Sinica, 2016, 65(20): 204101. doi: 10.7498/aps.65.204101 HE Hongjie and GUO Lixin. A multihybrid FE-BI-KA technique for 3-D electromagnetic scattering from a coated object above a conductive rough surface[J]. IEEE Geoscience and Remote Sensing Letters, 2016, 13(12): 2009–2013. doi: 10.1109/LGRS.2016.2621121 任新成, 朱小敏, 刘鹏. 雪层覆盖土壤表面与半埋柱体宽带复合散射FDTD方法[J]. 计算物理, 2017, 34(3): 327–334. doi: 10.3969/j.issn.1001-246X.2017.03.009REN Xincheng, ZHU Xiaomin, and LIU Peng. FDTD study on wide-band composite scattering from soil surface covered with snow and a partially buried column[J]. Chinese Journal of Computational Physics, 2017, 34(3): 327–334. 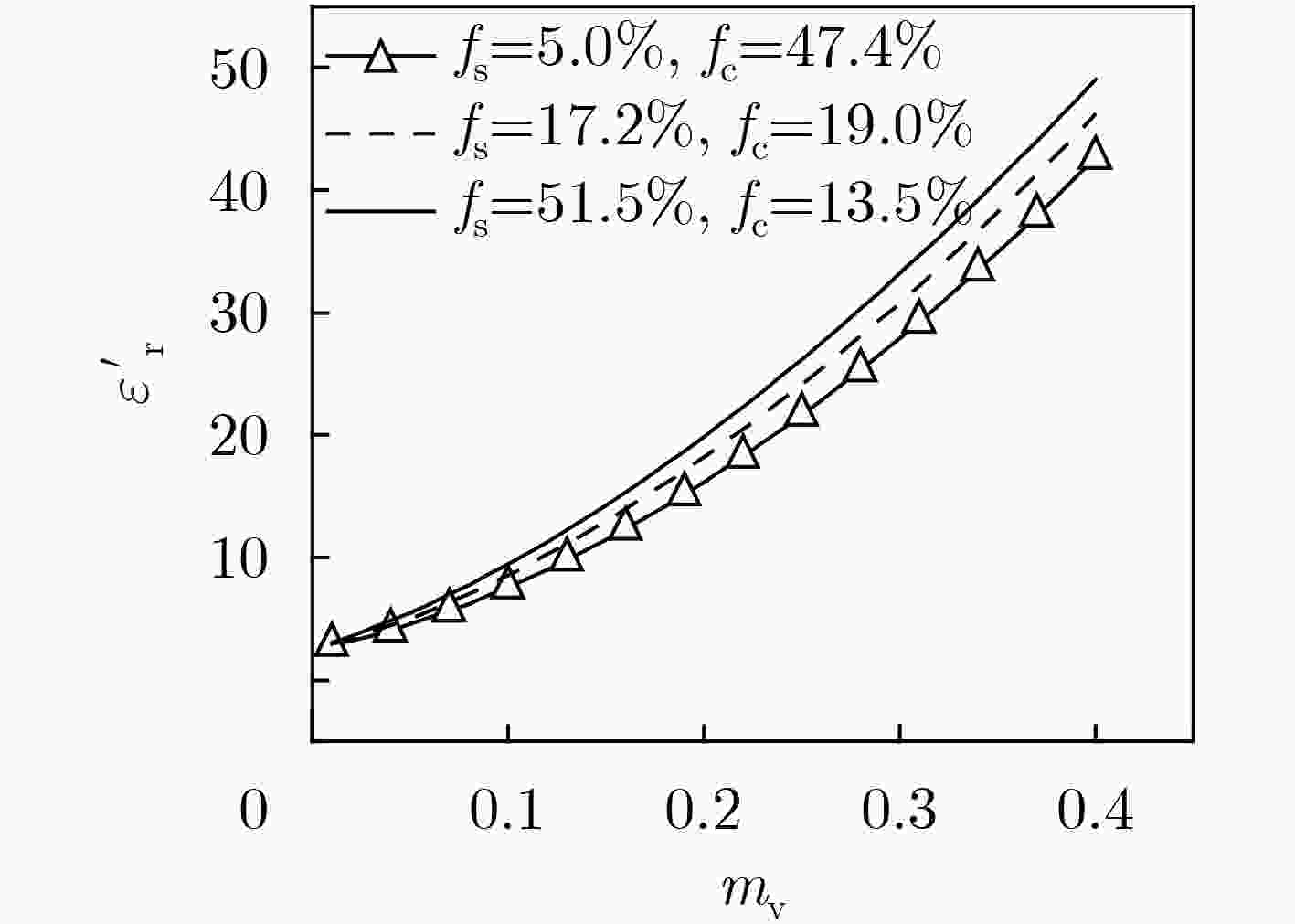doi: 10.3969/j.issn.1001-246X.2017.03.009 PEPLINSKI N R, ULABY F T, and DOBSON M C. Dielectric properties of soils in the 0.3-1.3-GHz range[J]. IEEE Transactions on Geoscience and Remote Sensing, 1995, 33(3): 803–807. doi: 10.1109/36.387598 曾江源, 李震, 陈权, 等. SAR土壤水分反演中的介电常数实部简化模型[J]. 红外与毫米波学报, 2012, 31(6): 556–562. doi: 10.3724/SP.J.1010.2012.00556ZENG Jiangyuan, LI Zhen, CHEN Quan, et al. A simplified model of the real part of the soil complex permittivity for soil moisture estimation from SAR image[J]. Journal of Infrared and Millimeter Waves, 2012, 31(6): 556–562. doi: 10.3724/SP.J.1010.2012.00556 WANG J R and SCHMUGGE T J. An empirical model for the complex dielectric permittivity of soils as a function of water content[J]. IEEE Transactions on Geoscience and Remote Sensing, 1980, GE-18(4): 288–295. doi: 10.1109/TGRS.1980.350304 刘军, 赵少杰, 蒋玲梅, 等. 微波波段土壤的介电常数模型研究进展[J]. 遥感信息, 2015, 30(1): 5–13, 70. doi: 10.3969/j.issn.1000-3177.2015.01.002LIU Jun, ZHAO Shaojie, JIANG Lingmei, et al. Research progress on dielectric constant model of soil at microwave frequency[J]. Remote Sensing Information, 2015, 30(1): 5–13, 70. doi: 10.3969/j.issn.1000-3177.2015.01.002 DUAN Xueyang and MOGHADDAM M. Full-wave electromagnetic scattering from rough surfaces with buried inhomogeneities[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(6): 3338–3353. doi: 10.1109/TGRS.2017.2669897 DARAWANKUL A and JOHNSON J T. Band-limited exponential correlation function for rough-surface scattering[J]. IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(5): 1198–1206. doi: 10.1109/tgrs.2007.893817 葛德彪, 闫玉波. 电磁波时域有限差分方法[M]. 3版. 西安: 西安电子科技大学出版社, 2011: 168–256.GE Debiao and YAN Yubo. Finite-Difference Time-Domain Method for Electromagnetic Waves[M]. 3rd ed. Xi’an: Xidian University Press, 2011: 168–256. 期刊类型引用(5)
1. 杨能勋，任新成，王玉清，朱小敏，董子宇. 横向沙丘表面与上方矩形截面柱复合电磁散射的FDTD研究. 现代电子技术. 2024(03): 143-148 . 
百度学术2. 陈玮，任新成，王玉清，赵晔，杨鹏举. 冻结土壤表面等边三角形截面柱运动目标复合电磁散射特性研究. 现代应用物理. 2024(05): 112-119 . 百度学术3. 方世妮，任新成，赵晔，杨鹏举，翟永智. 草原环境地表电磁散射的矩量法研究. 微波学报. 2023(03): 66-72 . 百度学术4. 王童，童创明，许光飞，彭鹏，王宜进. 基于电磁模型的宽带雷达海杂波信号建模与分析. 电子与信息学报. 2022(04): 1358-1365 . 
本站查看5. 关文涛，赵晔，任新成. 不同波段下海面电磁散射特性的研究. 延安大学学报(自然科学版). 2021(04): 66-70+74 . 百度学术其他类型引用(7)
-
下载:
下载:
百度学术
计量
- 文章访问数: 2240
- HTML全文浏览量: 1002
- PDF下载量: 65
- 被引次数: 12
下载:
