PSWFs Frequency Domain Modulation and Demodulation Method
-
摘要:
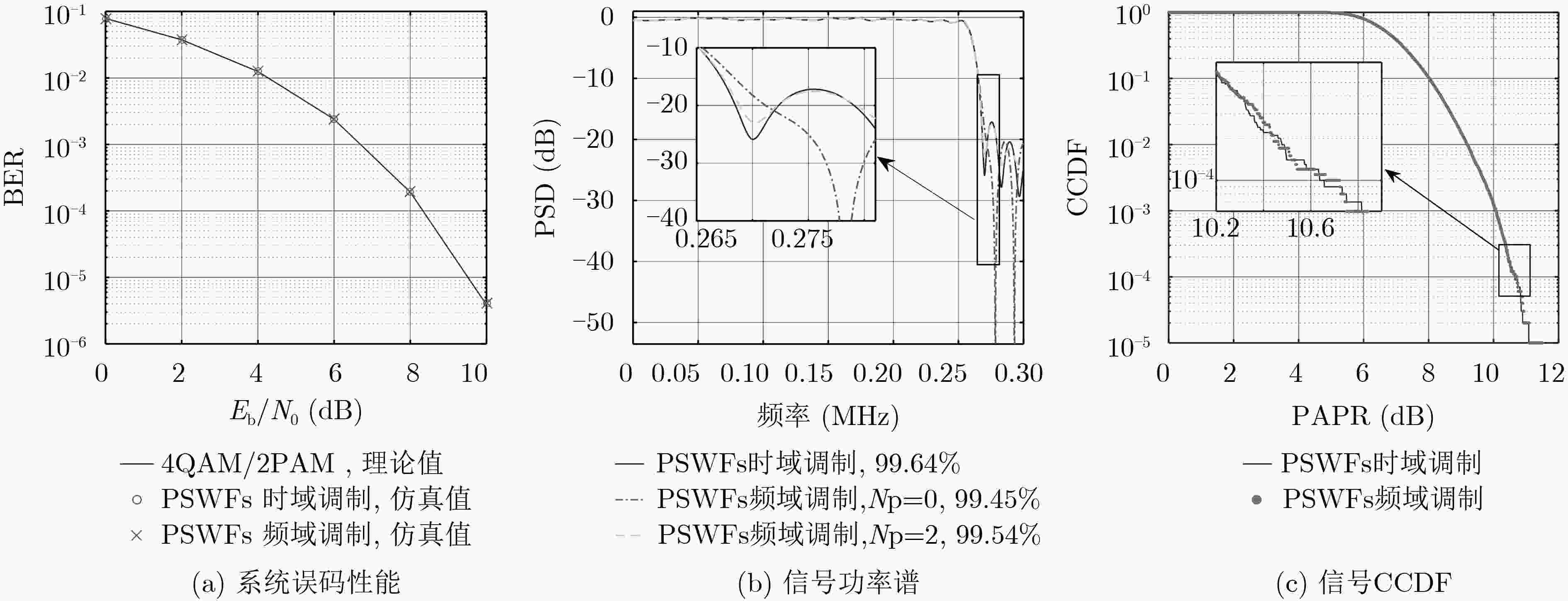
针对基于椭圆球面波函数(PSWFs)的非正弦时域调制算法复杂度高的不足,该文引入空间映射,分析了PSWFs信号频域完备正交性,推导出PSWFs信号频域有效表示所需最小抽样点数。在此基础上,引入复数域映射、FFT/IFFT信号处理框架,提出PSWFs频域调制解调方法。该方法将PSWFs信号处理由时域拓展到频域,在频域进行信息加载与检测,为探索研究PSWFs信号在5G、超5G等采用频域信号处理的通信系统中的应用提供了可能。理论和数值分析表明,相对于PSWFs时域调制,所提方法将能够在不改变系统频带利用率、系统误码性能、调制信号能量聚集性以及信号峰均功率比的前提下,显著降低算法复杂度,将运算复杂度由O(2Qg2)降低为O(g2+glog2g)。
-
关键词:
- 椭圆球面波函数 /
- 频域调制 /
- FFT/IFFT框架 /
- 频域抽样
Abstract:In view of the problem of high complexity for non-sinusoidal time domain modulation algorithms based on Prolate Spheroidal Wave Functions (PSWFs), spatial mapping is introduced to analyze the complete orthogonality and derive the minimum number of sampling points of PSWFs in the frequency domain. On this basis, the complex domain mapping and FFT/IFFT signal processing framework are introduced, and the PSWFs frequency domain modulation and demodulation method are proposed. The proposed method extends PSWFs signal processing from time domain to frequency domain, providing a possibility for exploring and studying the application of PSWFs signal to 5G, beyond 5G which use frequency domain signal processing. Theory and numerical analysis show that, compared with the time domain modulation, the proposed method can reduces the complexity of the algorithm from O(2Qg2) to O(g2+glog2g) without changing the system spectral efficiency, system error performance, modulation signal energy aggregation, and peak-to-average power ratio.
-
表 1 仿真参数设置
参数 符号 数值 信号时间带宽积 g 36 Hz·s 信号时宽 T 66.7 μs 信号频带范围 [0 0.27] MHz 信号路数c-k k 1 时域抽样点个数 NT 1024 频域总抽样点个数 NF g+1 增加抽样点数 NP 2 -
NISSEL R, SCHWARZ S, and RUPP M. Filter bank multicarrier modulation schemes for future mobile communications[J]. IEEE Journal on Selected Areas in Communications, 2017, 35(8): 1768–1782. doi: 10.1109/JSAC.2017.2710022 SOLDANI D, GUO Y J, BARANI B, et al. 5G for ultra-reliable low-latency communications[J]. IEEE Network, 2018, 32(2): 6–7. doi: 10.1109/MNET.2018.8329617 黄容兰, 刘云, 李啟尚, 等. 基于非正交多址接入中继通信系统的功率优化[J]. 电子与信息学报, 2019, 41(8): 1909–1915. doi: 10.11999/JEIT180842HUANG Ronglan, LIU Yun, LI Qishang, et al. Power allocation optimization of cooperative relaying systems using non-orthogonal multiple access[J]. Journal of Electronics &Information Technology, 2019, 41(8): 1909–1915. doi: 10.11999/JEIT180842 申滨, 吴和彪, 崔太平, 等. 基于最优索引广义正交匹配追踪的非正交多址系统多用户检测[J]. 电子与信息学报, 2020, 42(3): 621–628. doi: 10.11999/JEIT190270SHEN Bin, WU Hebiao, CUI Taiping, et al. An optimal number of indices aided gOMP algorithm for multi-user detection in NOMA system[J]. Journal of Electronics &Information Technology, 2020, 42(3): 621–628. doi: 10.11999/JEIT190270 王汝言, 梁颖杰, 崔亚平. 车辆网络多平台卸载智能资源分配算法[J]. 电子与信息学报, 2020, 42(1): 263–270. doi: 10.11999/JEIT190074WANG Ruyan, LIANG Yingjie, and CUI Yaping. Intelligent resource allocation algorithm for multi-platform offloading in vehicular networks[J]. Journal of Electronics &Information Technology, 2020, 42(1): 263–270. doi: 10.11999/JEIT190074 IBRAHIM M, DEMIR A F, and ARSLAN H. Time-frequency warped waveforms[J]. IEEE Communications Letters, 2019, 23(1): 36–39. doi: 10.1109/LCOMM.2018.2882498 SLEPIAN D and POLLAK H O. Prolate spheroidal wave functions, Fourier analysis and uncertainty-I[J]. The Bell System Technical Journal, 1961, 20(1): 43–63. doi: 10.1002/j.1538-7305.1961.tb03976.x 王红星, 陆发平, 刘传辉, 等. 椭圆球面波信号间交叉项时频分布特性研究[J]. 电子与信息学报, 2017, 39(6): 1319–1325. doi: 10.11999/JEIT160877WANG Hongxing, LU Faping, LIU Chuanhui, et al. Study on time-frequency characteristics of cross-terms between prolate spheroidal wave function signal[J]. Journal of Electronics &Information Technology, 2017, 39(6): 1319–1325. doi: 10.11999/JEIT160877 OSIPOV A, ROKHLIN V, and XIAO Hong. Prolate Spheroidal Wave Functions of Order Zero: Mathematical Tools for Bandlimited Approximation[M]. Boston: Springer, 2013: 33–66. doi: 10.1007/978-1-4614-8259-8. CHEN Zhaonan, WANG Hongxing, LIU Xiguo, et al. Maximal capacity nonorthogonal pulse shape modulation[J]. Chinese Journal of Aeronautics, 2015, 28(6): 1699–1708. doi: 10.1016/j.cja.2015.09.008 SLEPIAN D. Prolate spheroidal wave functions, Fourier analysis, and uncertainty-V: The discrete case[J]. The Bell System Technical Journal, 1978, 57(5): 1371–1430. doi: 10.1002/j.1538-7305.1978.tb02104.x SELINIS I, KATSAROS K, ALLAYIOTI M, et al. The race to 5G era; LTE and Wi-Fi[J]. IEEE Access, 2018, 6: 56598–56636. doi: 10.1109/ACCESS.2018.2867729 HAMMOODI A, AUDAH L, and TAHER M A. Green coexistence for 5G waveform candidates: A review[J]. IEEE Access, 2019, 7: 10103–10126. doi: 10.1109/ACCESS.2019.2891312 HARMUTH H F. Frequency-sharing and spread-spectrum transmission with large relative bandwidth[J]. IEEE Transactions on Electromagnetic Compatibility, 1978, EMC-20(1): 232–239. doi: 10.1109/TEMC.1978.303653 -





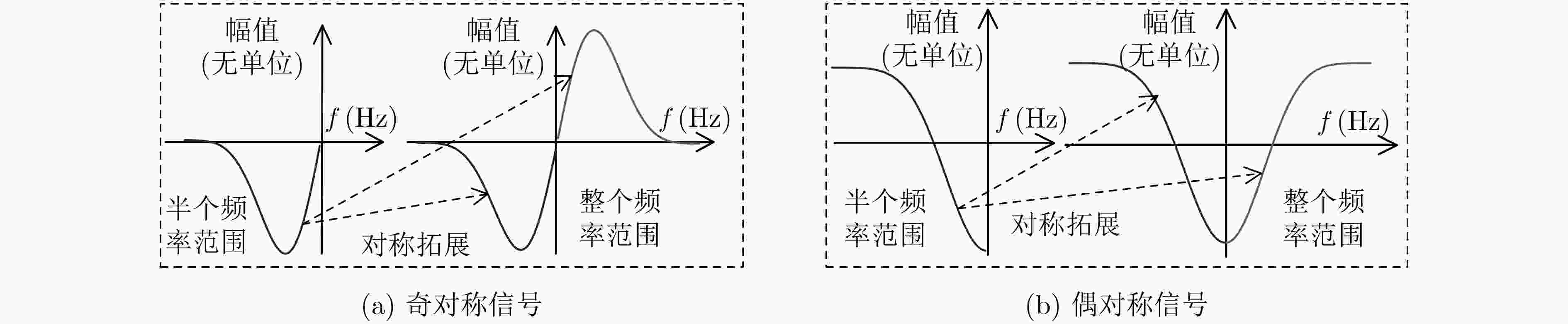
 下载:
下载:
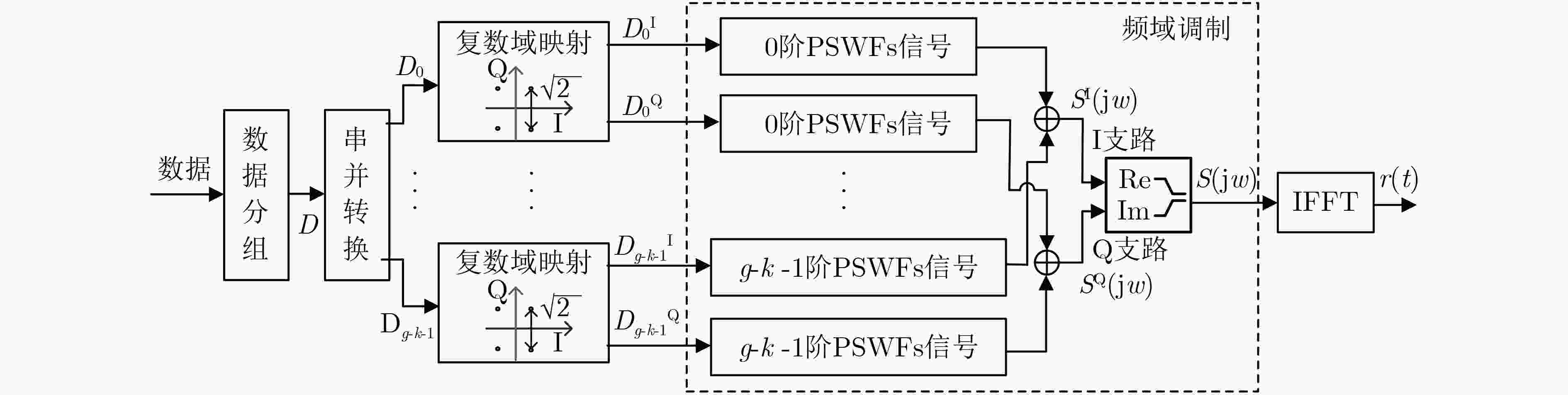
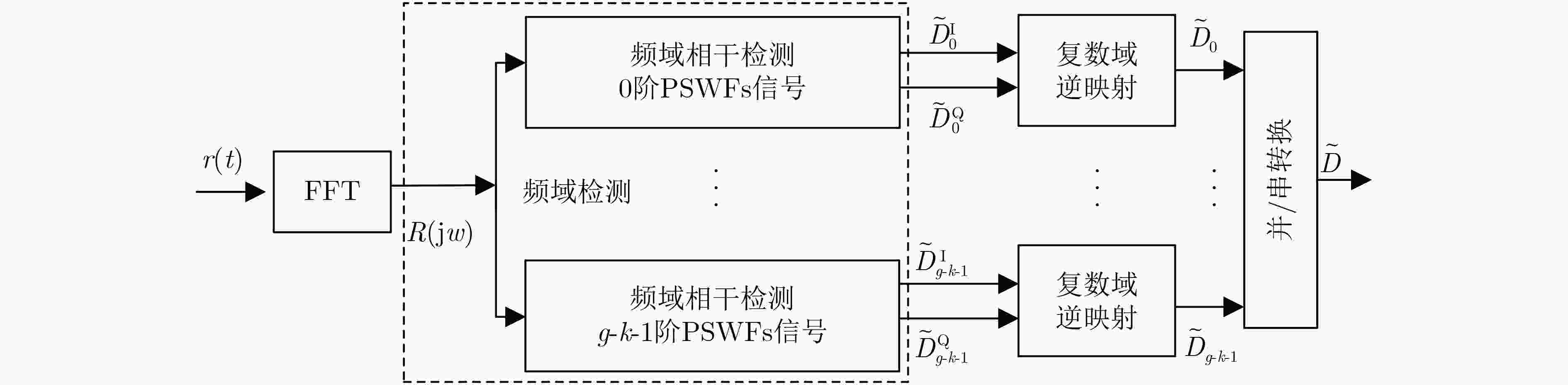
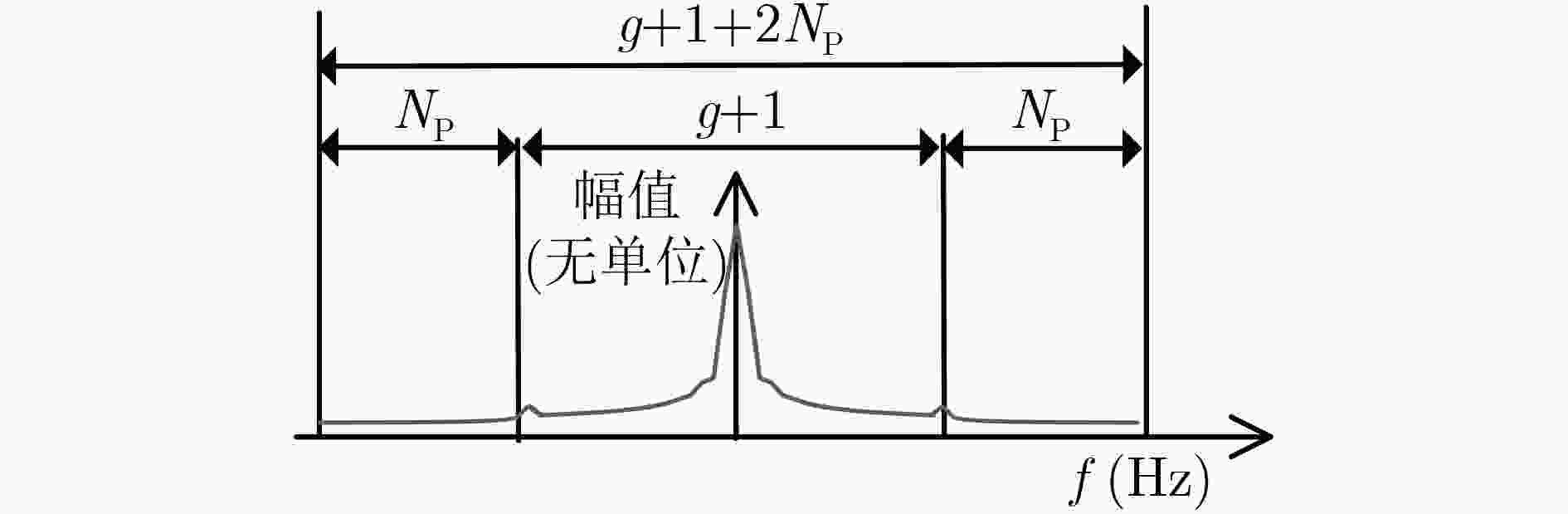


 下载:
下载:
