改进的Type-1型广义Feistel结构的量子攻击及其在分组密码CAST-256上的应用

倪博煜; 董晓阳

doi:10.11999/JEIT190633

改进的Type-1型广义Feistel结构的量子攻击及其在分组密码CAST-256上的应用

doi: 10.11999/JEIT190633

倪博煜^{1, 2},
董晓阳^3, ,

1.
山东大学密码技术与信息安全教育部重点实验室济南 250100
2.
山东大学网络空间安全学院青岛 266237
3.
清华大学高等研究院北京 100084

基金项目: 国家重点研发计划(2017YFA0303903)，国家自然科学基金(61902207)，国家密码发展基金(MMJJ20180101, MMJJ20170121)

详细信息

作者简介:
董晓阳：男，1988年生，助理研究员。研究方向为对称密码算法的安全性分析与设计

通讯作者:
董晓阳　xiaoyangdong@tsinghua.edu.cn

中图分类号: TN918; TP309
计量
- 文章访问数: 3202
- HTML全文浏览量: 941
- PDF下载量: 137
- 被引次数: 0
出版历程
- 收稿日期: 2019-08-26
- 修回日期: 2019-11-26
- 网络出版日期: 2019-11-29
- 刊出日期: 2020-02-19

Improved Quantum Attack on Type-1 Generalized Feistel Schemes and Its Application to CAST-256

Boyu NI^{1, 2},
Xiaoyang DONG^{3
, ,}

1.
Key Laboratory of Cryptologic Technology and Information Security, Ministry of Education, Shandong University, Jinan 250100, China
2.
School of Cyber Science and Technology, Shandong University, Qingdao 266237, China
3.
Institute for Advanced Study, Tsinghua University, Beijing 100084, China

Funds: The National Key Research and Development Program of China (2017YFA0303903), The National Natural Science Foundation of China (61902207), The National Cryptography Development Fund (MMJJ20180101, MMJJ20170121)

摘要

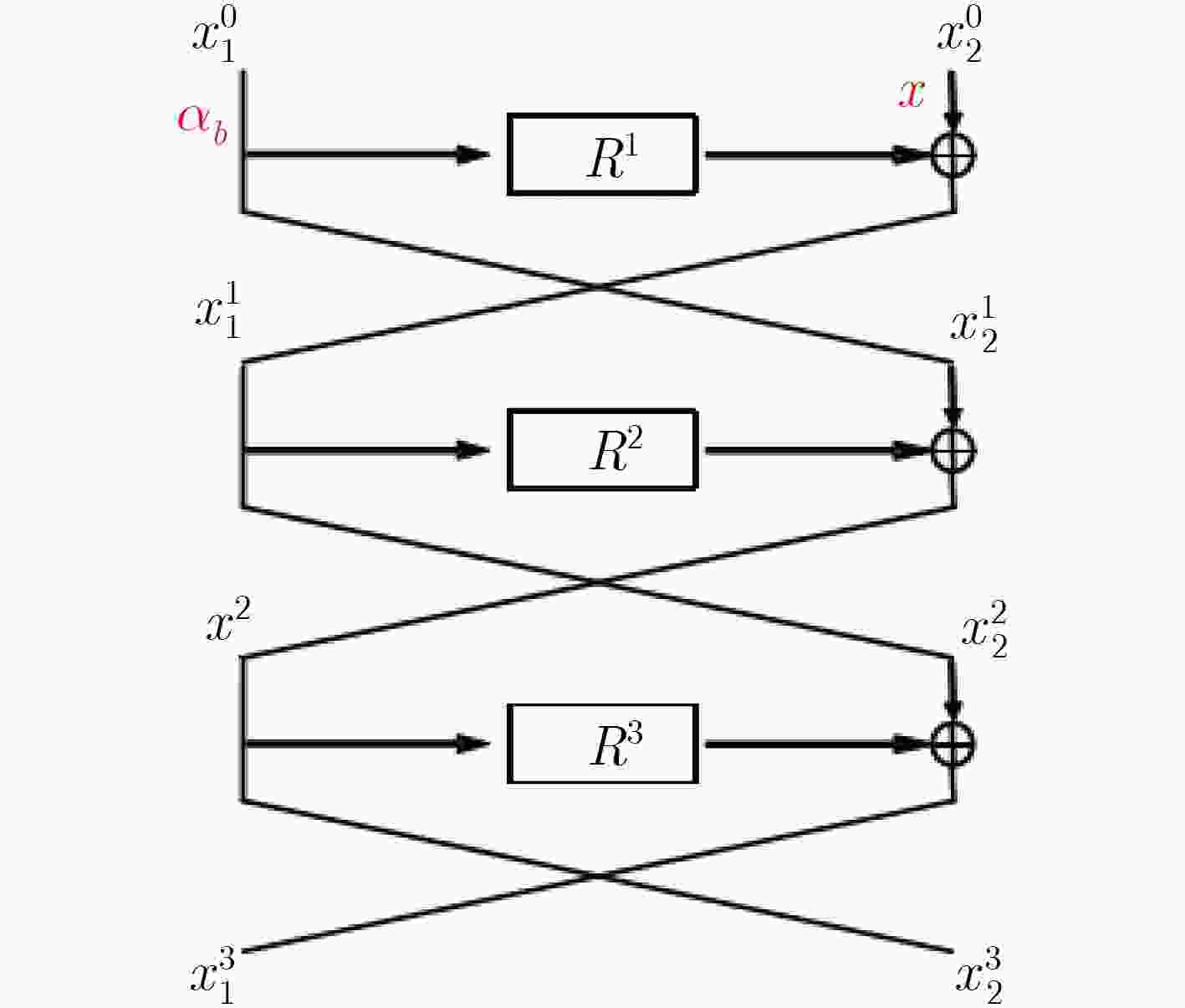
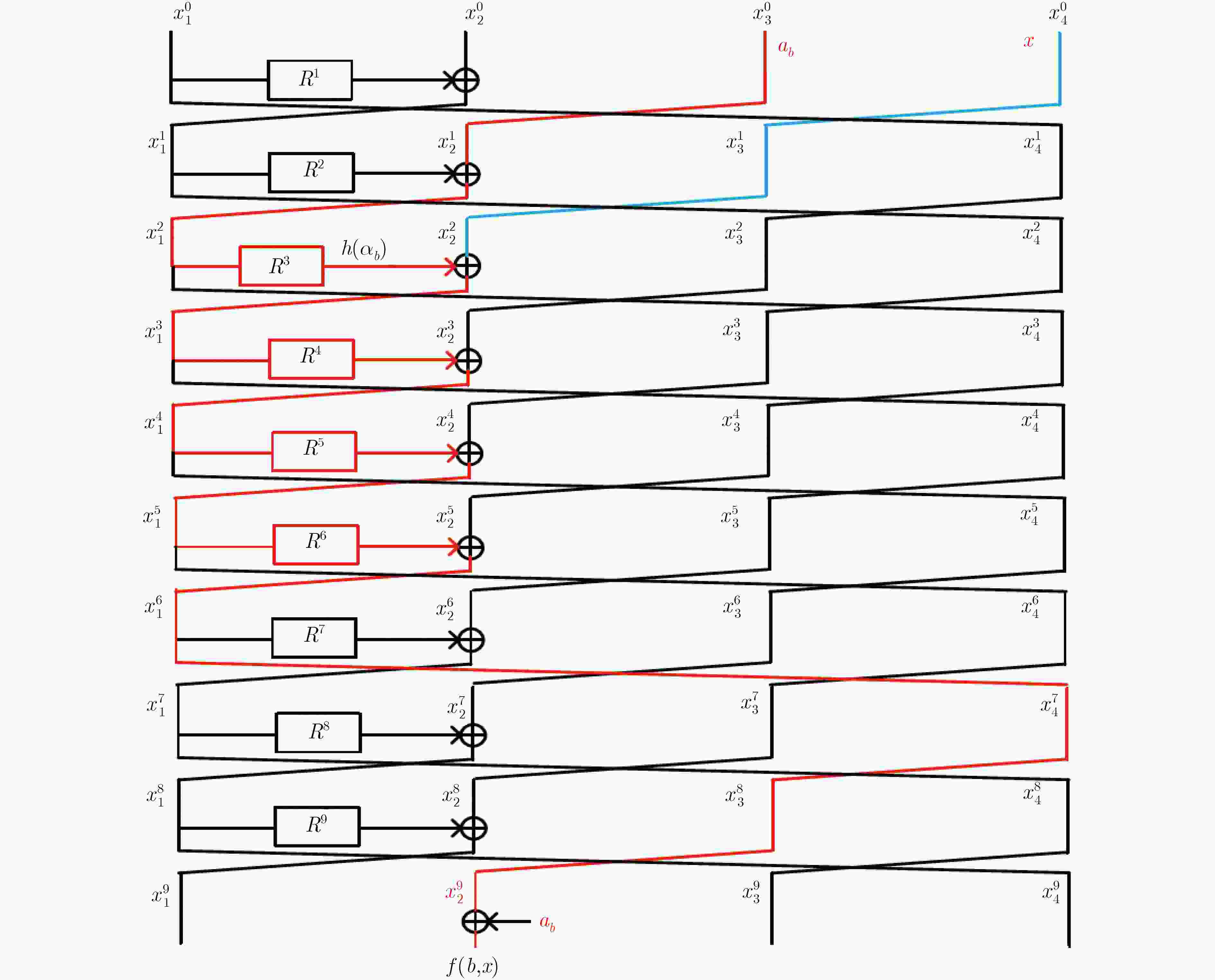
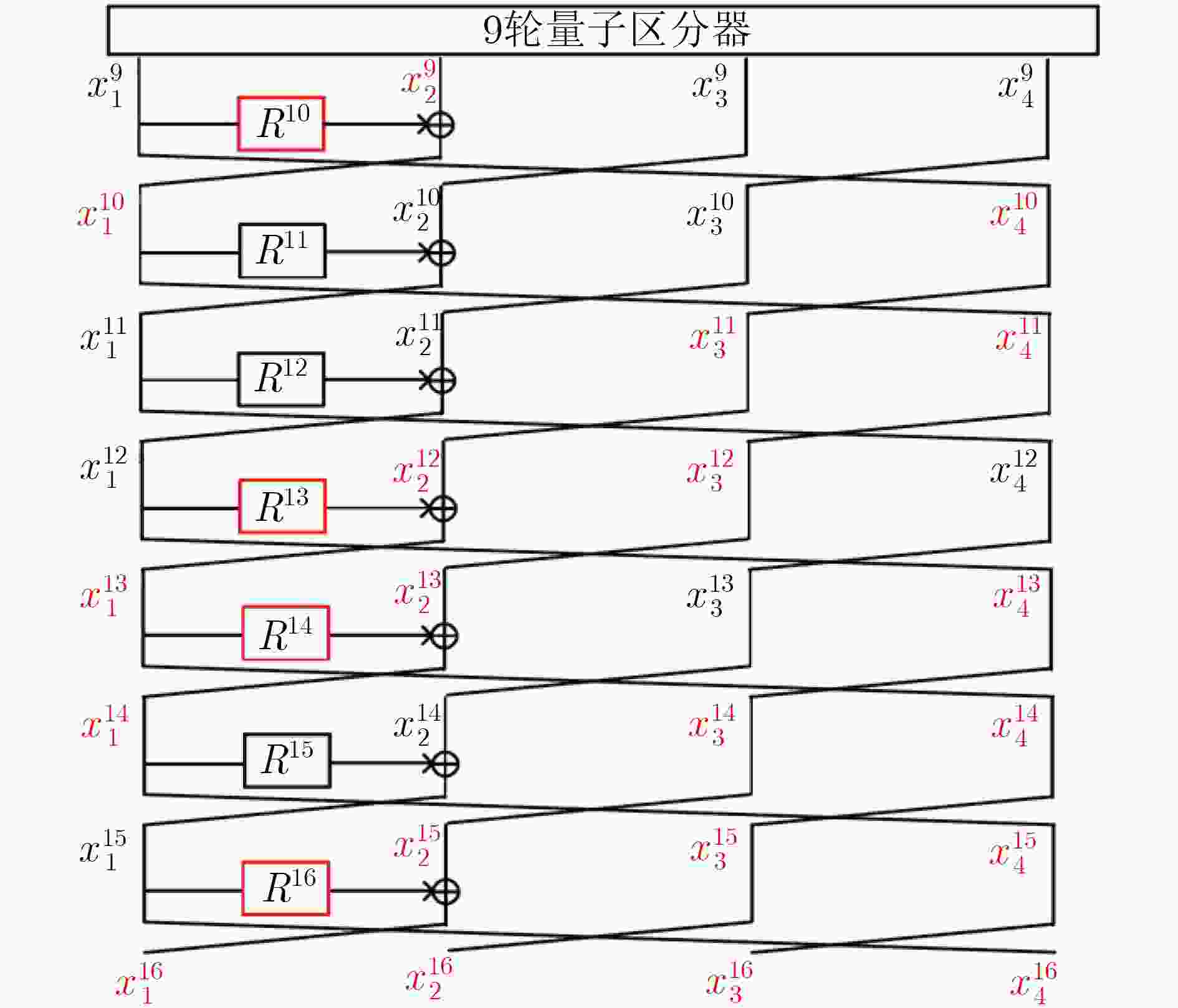
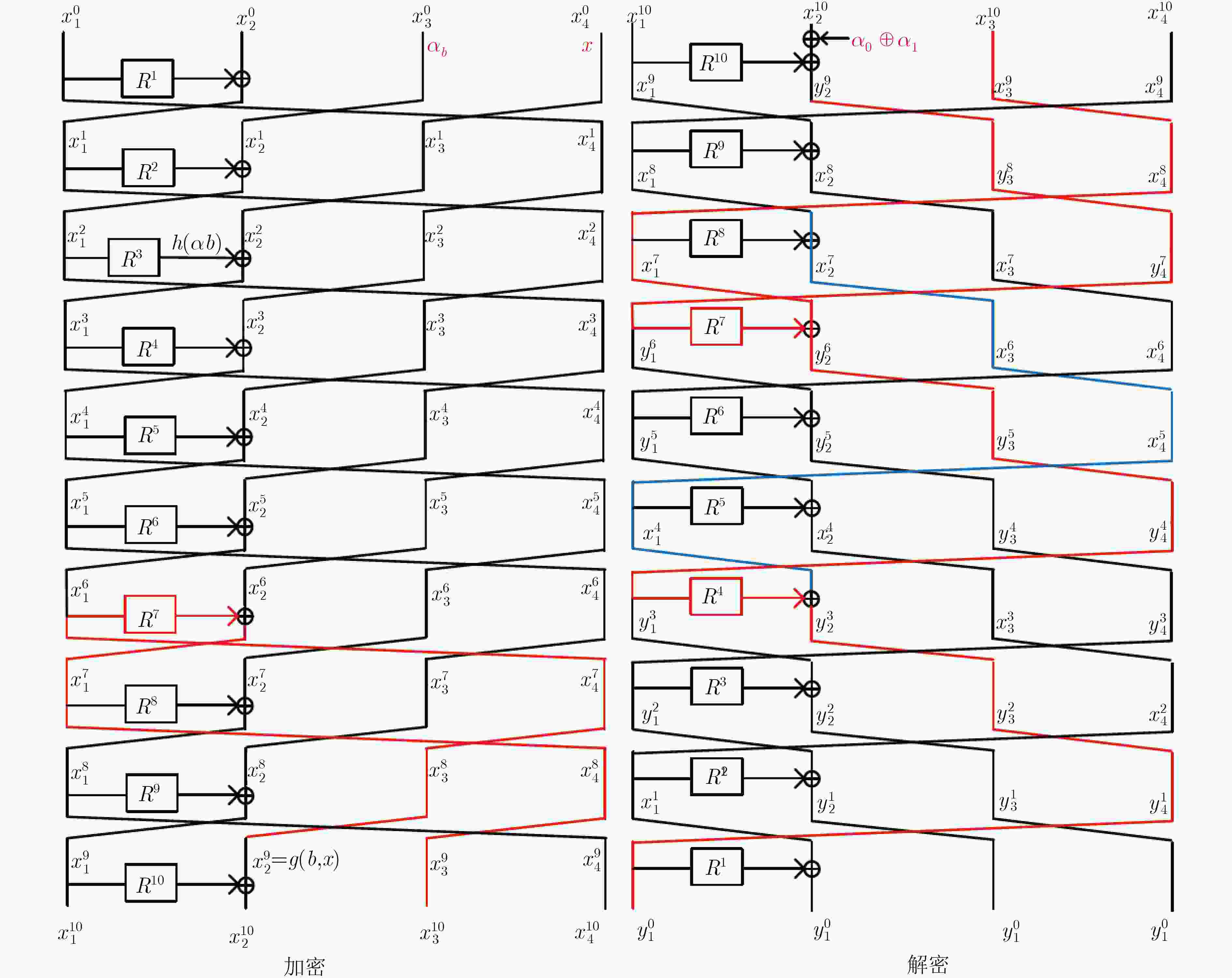
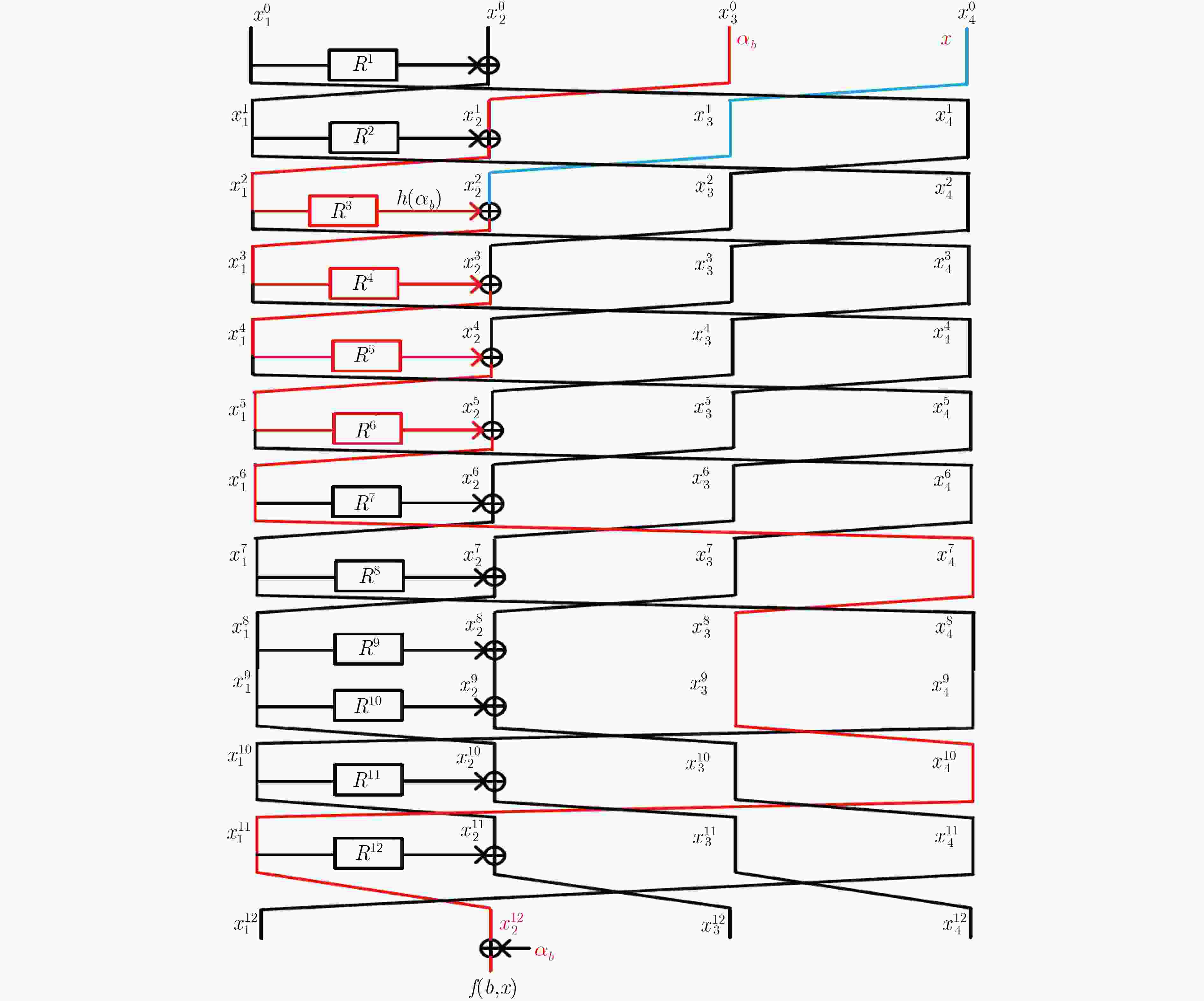
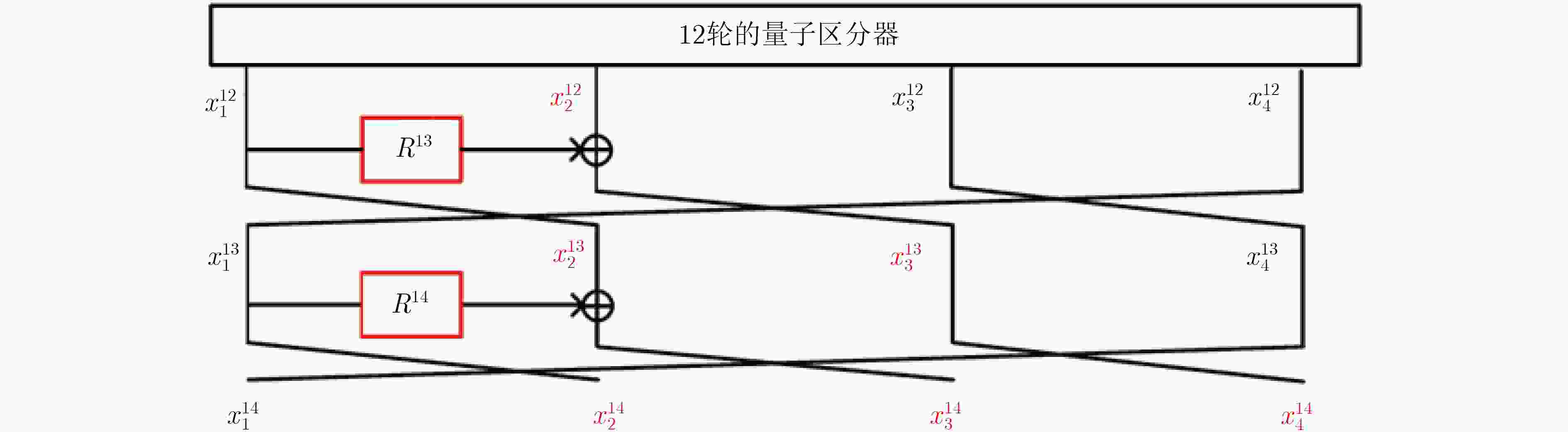
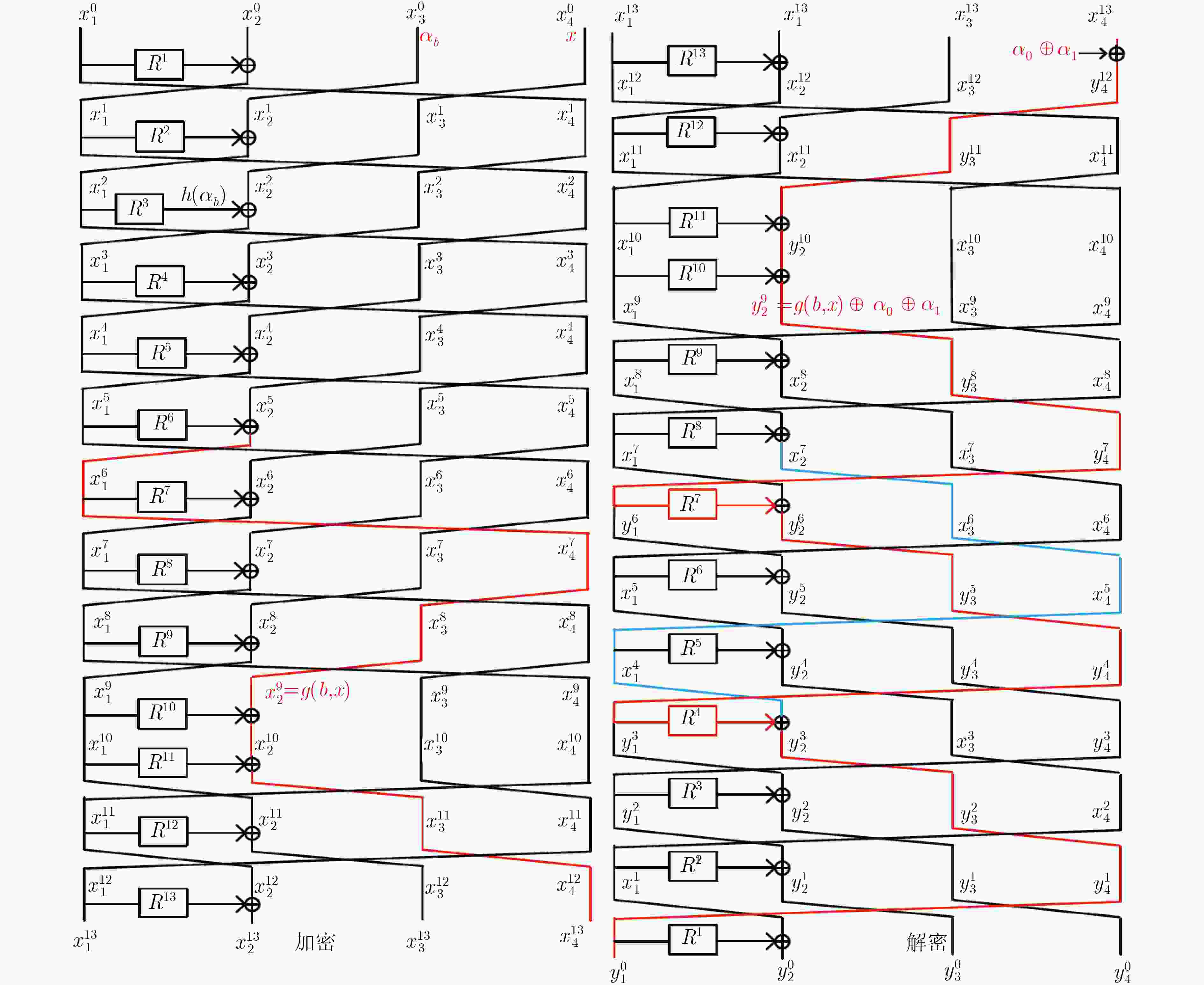
摘要: 广义Feistel结构(GFS)是设计对称密码算法的重要基础结构之一，其在经典计算环境中受到了广泛的研究。但是，量子计算环境下对GFS的安全性评估还相当稀少。该文在量子选择明文攻击(qCPA)条件下和量子选择密文攻击(qCCA)条件下，分别对Type-1 GFS进行研究，给出了改进的多项式时间量子区分器。在qCPA条件下，给出了3d – 3轮的多项式时间量子区分攻击，其中$d(d \ge 3)$是Type-1 GFS的分支数，攻击轮数较之前最优结果增加$d - 2$轮。得到更好的量子密钥恢复攻击，即相同轮数下攻击的时间复杂度降低了${2^{(d - 2)n/2}}$。在qCCA条件下，对于Type-1 GFS给出了$3d - 2$轮的多项式时间量子区分攻击，比之前最优结果增加了$d - 1$轮。该文将上述区分攻击应用到CAST-256分组密码中，得到了12轮qCPA多项式时间量子区分器，以及13轮qCCA多项式时间量子区分器，该文给出19轮CAST-256的量子密钥恢复攻击。
- 分组密码 /
- 广义Feistel结构 /
- 量子攻击 /
- CAST-256加密算法
Abstract: Generalized Feistel Schemes (GFS) are important components of symmetric ciphers, which have been extensively researched in classical setting. However, the security evaluations of GFS in quantum setting are rather scanty. In this paper, more improved polynomial-time quantum distinguishers are presented on Type-1 GFS in quantum Chosen-Plaintext Attack (qCPA) setting and quantum Chosen-Ciphertext Attack (qCCA) setting. In qCPA setting, new quantum polynomial-time distinguishers are proposed on $3d - 3$ round Type-1 GFS with branches $d \ge 3$, which gain $d - 2$ more rounds than the previous distinguishers. Hence, key- recovery attacks can be obtained, whose time complexities gain a factor of ${2^{\frac{{\left( {d - 2} \right)n}}{2}}}$. In qCCA setting, $3d - 3$ round quantum distinguishers can be obtained on Type-1 GFS, which gain $d-1$ more rounds than the previous distinguishers. In addition, given some quantum attacks on CAST-256 block cipher. 12-round and 13-round polynomial-time quantum distinguishers are obtained in qCPA and qCCA settings, respectively. Hence, the quantum key-recovery attack on 19-round CAST-256 is derived.
- Block cipher /
- Generalized Feistel Scheme (GFS) /
- Quantum attack /
- CAST-256 cipher algorithm

HTML全文

图 1 3轮的量子区分器

下载: 全尺寸图片幻灯片

图 2 FX结构

下载: 全尺寸图片幻灯片

图 3 Ito等人在Feistel上的4轮量子区分器

下载: 全尺寸图片幻灯片

图 4 $d$分支Type-1 GFS的第$i$轮

下载: 全尺寸图片幻灯片

图 5 4分支Type-1 GFS的选择明文量子区分器

下载: 全尺寸图片幻灯片

图 6 4分支Type-1 GFS的16轮密钥恢复攻击

下载: 全尺寸图片幻灯片

图 7 4分支CAST256-like GFS的10轮区分器

下载: 全尺寸图片幻灯片

图 8 CAST-256的12轮区分器

下载: 全尺寸图片幻灯片

图 9 CAST-256的14轮攻击

下载: 全尺寸图片幻灯片

图 10 CAST-256的13轮区分器

下载: 全尺寸图片幻灯片

表 1 Type-1 GFS的量子区分器的轮数

来源	攻击条件	$r$	$d = 3$	$d = 4$	$d = 5$	$d = 6$	$d = 7$
文献[35]	qCPA	2d–1	5	7	9	11	13
4.1节	qCPA	3d–3	6	9	12	15	18
4.2节	qCCA	3d–2	7	10	13	16	19

下载: 导出CSV

表 2 在量子环境下对Type-1 GFS的密钥恢复攻击

来源	区分器轮数	密钥恢复轮数	复杂度(log)	穷搜复杂度(log)
文献[35]	$2d - 1$	$r \ge {d^2}$	$T + ({{r - {d^2} + d - 2)n} / 2}$	${{rn} / 2}$
4.1节	$3d - 3$	$r \ge {d^2}$	$T + ({{r - {d^2})n} / 2}$	${{rn} / 2}$

下载: 导出CSV

表 3 CAST-256的量子攻击

来源	攻击条件	区分器轮数	密钥恢复攻击轮数
来源	攻击条件	区分器轮数	$r = 14$	$r = 15$	$r = 16$	$r = 17$	$r = 18$	$r = 19$
文献[35]	qCPA	7	${2^{74}}$	${2^{92.5}}$	${2^{111}}$	$ - $	$ - $	$ - $
5.1节	qCPA	12	${2^{37}}$	${2^{55.5}}$	${2^{74}}$	${2^{92.5}}$	${2^{111}}$	$ - $
5.2节	qCCA	13	${2^{18.5}}$	${2^{37}}$	${2^{55.5}}$	${2^{74}}$	${2^{92.5}}$	${2^{111}}$

下载: 导出CSV

表 4 针对CAST-256的经典攻击和量子攻击的比较

来源	密钥长度	攻击	轮数	数据	时间
文献[39]	128	飞去来器	16	${2^{49.3}}$	$ - $
5.2节	128	qCCA	16	–	$ {2^{55.5}} $
文献[40]	192	线性攻击	24	${2^{124.1}}$	$ {2^{156.52}} $
5.2节	192	qCCA	17	–	$ {2^{74}}$
文献[41]	256	多维零相关	28	${2^{98.8}}$	$ {2^{246.9}} $
5.2节	256	qCCA	19	–	$ {2^{111}} $

下载: 导出CSV

参考文献(41)

KNUDSEN L R. The security of Feistel ciphers with six rounds or less[J]. Journal of Cryptology, 2002, 15(3): 207–222. doi: 10.1007/s00145-002-9839-y

ISOBE T and SHIBUTANI K. Generic key recovery attack on Feistel scheme[C]. The 19th International Conference on the Theory and Application of Cryptology and Information Security, Bengaluru, India, 2013: 464–485.

GUO Jian, JEAN J, NIKOLIĆ I, et al. Meet-in-the-middle attacks on generic Feistel constructions[C]. The 20th International Conference on the Theory and Application of Cryptology and Information Security, Kaoshiung, China, 2014: 458–477.

DINUR I, DUNKELMAN O, KELLER N, et al. New attacks on Feistel structures with improved memory complexities[C]. The 35th Annual Cryptology Conference, Santa Barbara, USA, 2015: 433–454.

AOKI K, ICHIKAWA T, KANDA M, et al. Camellia: A 128-bit Block Cipher Suitable for Multiple Platforms - Design and Analysis[M]. Berlin, Heidelberg: Springer, 2001: 39–56.

National Soviet Bureau of Standards. GOST 28147-89 Information processing systems. cryptographic protection cryptographic transformation algorithm[S]. 1989.

ZHENG Yuliang, MATSUMOTO T, and IMAI H. On the construction of block ciphers provably secure and not relying on any unproved hypotheses[C]. Conference on the Theory and Application of Cryptology, Santa Barbara, USA, 1990: 461–480.

ANDERSON R and BIHAM E. Two practical and provably secure block ciphers: BEAR and LION[C]. The 3rd International Workshop on Fast Software Encryption, Cambridge, UK, 1996: 113–120.

LUCKS S. Faster luby-rackoff ciphers[C]. The 3rd International Workshop on Fast Software Encryption, Cambridge, UK, 1996: 189–203.

SCHNEIER B and KELSEY J. Unbalanced Feistel networks and block cipher design[C]. The 3rd International Workshop on Fast Software Encryption, Cambridge, UK, 1996: 121–144.

First AES Candidate Conference[EB/OL]. http://csrc.nist.gov/archive/aes/round1/conf1/aes1conf.htm.

SHIRAI T, SHIBUTANI K, AKISHITA T, et al. The 128-bit blockcipher CLEFIA (extended abstract)[C]. The 14th International Workshop on Fast Software Encryption, Luxembourg, Luxembourg, 2007: 181–195.

GUERON S and MOUHA N. Simpira v2: A family of efficient permutations using the AES round function[C]. The 22nd International Conference on the Theory and Application of Cryptology and Information Security, Hanoi, Vietnam, 2016: 95–125.

LUBY M and RACKOFF C. How to construct pseudorandom permutations from pseudorandom functions[J]. SIAM Journal on Computing, 1988, 17(2): 373–386. doi: 10.1137/0217022

MORIAI S and VAUDENAY S. On the pseudorandomness of top-level schemes of block ciphers[C]. The 6th International Conference on the Theory and Application of Cryptology and Information Security, Kyoto, Japan, 2000: 289–302.

HOANG V T and ROGAWAY P. On generalized Feistel networks[C]. The 30th Annual Cryptology Conference, Santa Barbara, USA, 2010: 613–630.

JUTLA C S. Generalized birthday attacks on unbalanced Feistel networks[C]. The 18th Annual International Cryptology Conference, Santa Barbara, USA, 1998: 186–199.

GUO Jian, JEAN J, NIKOLIC I, et al. Meet-in-the-middle attacks on classes of contracting and expanding Feistel constructions[J]. IACR Transactions on Symmetric Cryptology, 2016(2): 307–337.

NACHEF V, VOLTE E, and PATARIN J. Differential attacks on generalized Feistel schemes[C]. The 12th International Conference on Cryptology and Network Security, Paraty, Brazil, 2013: 1–19.

TJUAWINATA I, HUANG Tao, and WU Hongjun. Improved differential cryptanalysis on generalized Feistel schemes[C]. The 18th International Conference on Cryptology in India, Chennai, India, 2017: 302–324.

PATARIN J, NACHEF V, and BERBAIN C. Generic attacks on unbalanced Feistel schemes with contracting functions[C]. The 12th International Conference on the Theory and Application of Cryptology and Information Security, Shanghai, China, 2006: 396–411.

PATARIN J, NACHEF V, and BERBAIN C. Generic attacks on unbalanced Feistel schemes with expanding functions[C]. The 13th International Conference on the Theory and Application of Cryptology and Information Security, Kuching, Malaysia, 2007: 325–341.

VOLTE E, NACHEF V, and PATARIN J. Improved generic attacks on unbalanced Feistel schemes with expanding functions[C]. The 16th International Conference on the Theory and Application of Cryptology and Information Security, Singapore, 2010: 94–111.

GROVER L K. A fast quantum mechanical algorithm for database search[C]. The 28th Annual ACM Symposium on Theory of Computing, Philadelphia, USA, 1996: 212–219.

KUWAKADO H and MORII M. Quantum distinguisher between the 3-round Feistel cipher and the random permutation[C]. IEEE International Symposium on Information Theory, Austin, USA, 2010: 2682–2685.

SIMON D R. On the power of quantum computation[J]. SIAM Journal on Computing, 1997, 26(5): 1474–1483. doi: 10.1137/S0097539796298637

KUWAKADO H and MORII M. Security on the quantum-type even-mansour cipher[C]. 2012 International Symposium on Information Theory and its Applications, Honolulu, USA, 2012: 312–316.

KAPLAN M, LEURENT G, LEVERRIER A, et al. Breaking symmetric cryptosystems using quantum period finding[C]. The 36th Annual International Cryptology Conference, Santa Barbara, USA, 2016: 207–237.

BONNETAIN X. Quantum key-recovery on full AEZ[C]. The 24th International Conference on Selected Areas in Cryptography, Ottawa, Canada, 2018: 394–406.

LEANDER G and MAY A. Grover meets simon - quantumly attacking the FX-construction[C]. The 23rd International Conference on the Theory and Applications of Cryptology and Information Security, Hong Kong, China, 2017: 161–178.

ZHANDRY M. How to construct quantum random functions[C]. The 53rd IEEE Annual Symposium on Foundations of Computer Science, New Brunswick, USA, 2012: 679–687.

ITO G, HOSOYAMADA A, MATSUMOTO R, et al. Quantum chosen-ciphertext attacks against Feistel ciphers[C]. The Cryptographers' Track at the RSA Conference, San Francisco, USA, 2019: 391–411.

HOSOYAMADA A and SASAKI Y. Quantum demiric-selçuk meet-in-the-middle attacks: Applications to 6-round generic Feistel constructions[C]. The 11th International Conference on Security and Cryptography for Networks, Amalfi, Italy, 2018: 386–403.

DONG Xiaoyang and WANG Xiaoyun. Quantum key-recovery attack on Feistel structures[J]. Science China Information Sciences, 2018, 61(10): 102501. doi: 10.1007/s11432-017-9468-y

DONG Xiaoyang, LI Zheng, and WANG Xiaoyun. Quantum cryptanalysis on some generalized Feistel schemes[J]. Science China Information Sciences, 2019, 62(2): 22501. doi: 10.1007/s11432-017-9436-7

DONG Xiaoyang, DONG Bingyou, and WANG Xiaoyun. Quantum attacks on some Feistel block ciphers[R]. Cryptology ePrint Archive, Report 2018/504, 2018.

BONNETAIN X, NAYA-PLASENCIA M, and SCHROTTENLOHER A. On quantum slide attacks[R]. Cryptology ePrint Archive, Report 2018/1067, 2018.

HOSOYAMADA A and IWATA T. Tight quantum security bound of the 4-round luby-rackoff construction[R]. Cryptology ePrint Archive, Report 2019/243, 2019.

WAGNER D. The boomerang attack[C]. The 6th International Workshop on Fast Software Encryption, Rome, Italy, 1999: 156–170.

WANG Meiqin, WANG Xiaoyun, and HU Changhui. New linear cryptanalytic results of reduced-round of CAST-128 and CAST-256[C]. The 15th International Workshop on Selected Areas in Cryptography, Sackville, Canada, 2009: 429–441.

BOGDANOV A, LEANDER G, NYBERG K, et al. Integral and multidimensional linear distinguishers with correlation zero[C]. The 18th International Conference on the Theory and Application of Cryptology and Information Security, Beijing, China, 2012: 244–261.

施引文献

资源附件(0)

访问统计