Bursting, Coexistence Analysis and DSP Implementation of Duffing System Based on Hyperbolic-tangent Memristor
-
摘要: 忆阻器作为第4种基本电路元件由蔡少棠首次提出，它的提出为混沌电路的设计和工程应用提供了新思路。该文通过在Homles型Duffing系统中引入一个双曲正切忆阻模型，得到了一个新忆阻Duffing非自治系统。利用转换相图、相图、Lyapunov指数等，揭示了该系统具有振荡尖峰数目可控簇发、非完全对称双边簇发、非完全对称的簇发共存、多种周期混沌共存等新颖动力学行为。并通过分岔图及平衡点分析，研究了其簇发产生机理。采用Multisim电路仿真与数字信号处理平台(DSP)对系统进行了硬件实现，与理论分析基本一致的实验结果证明该系统是可行的且是物理可实现的。Abstract: Memristor is first proposed by Chua as the fourth basic circuit element, which provides a novel idea for the design and engineering application of chaotic circuits. A novel memristive Duffing nonautonomous system is obtained by introducing a hyperbolic-tangent memristor into the Homles type Duffing system. By using the transformed phase portraits, phase portraits, Lyapunov exponents, etc., it is revealed that the system has novel dynamical behaviors such as bursts with controllable number of oscillation spikes, non-completely symmetrical bilateral bursts, coexistence of non-completely symmetrical bursts, multiple coexistence of chaos and period. The mechanism of bursting is studied by analysis of equilibrium point and bifurcation diagram. Multisim circuit simulation and Digital Signal Processing platform (DSP) are used to implement the system in hardware, and the experimental results basically consistent with the theoretical analysis prove that the system is feasible and physically achievable.
-
Key words:
- Memristor /
- Duffing /
- Bursting /
- Delayed bifurcation /
- Coexistence
-
STRUKOV D B, SNIDER G S, STEWART G R, et al. The missing memristor found[J]. Nature, 2008, 453(1): 80–83. doi: 10.1038/nature06932 CHUA L. Memristor-the missing circuit element[J]. IEEE Transactions on Circuit Theory, 1971, 18(5): 507–519. doi: 10.1109/tct.1971.1083337 王春华, 蔺海荣, 孙晶如, 等. 基于忆阻器的混沌、存储器及神经网络电路研究进展[J]. 电子与信息学报, 2020, 42(4): 795–810. doi: 10.11999/JEIT190821WANG Chunhua, LIN Hairong, SUN Jingru, et al. Research progress on chaos, memory and neural network circuits based on memristor[J]. Journal of Electronics &Information Technology, 2020, 42(4): 795–810. doi: 10.11999/JEIT190821 ZHOU Ling, WANG Chunhua, and ZHOU Lili. Generating hyperchaotic multi-wing attractor in a 4D memristive circuit[J]. Nonlinear Dynamics, 2016, 85(4): 2653–2663. doi: 10.1007/s11071-016-2852-8 YUAN Fang, WANG Guangyi, and WANG Xiaowei. Extreme multistability in a memristor-based multi-scroll hyper-chaotic system[J]. Chaos: An Interdisciplinary Journal of Nonlinear Science, 2016, 26(7): 073107. doi: 10.1063/1.4958296 阮静雅, 孙克辉, 牟俊. 基于忆阻器反馈的Lorenz超混沌系统及其电路实现[J]. 物理学报, 2016, 65(19): 25–35. doi: 10.7498/aps.65.190502RUAN Jingya, SUN Kehui, and MOU Jun. Memristor-based Lorenz hyper-chaotic system and its circuit implementation[J]. Acta Physica Sinica, 2016, 65(19): 25–35. doi: 10.7498/aps.65.190502 WANG Chunhua, LIU Xiaoming, and XIA Hu. Multi-piecewise quadratic nonlinearity memristor and its 2N-scroll and 2N +1-scroll chaotic attractors system[J]. Chaos: An Interdisciplinary Journal of Nonlinear Science, 2017, 27(3): 033114. doi: 10.1063/1.4979039 肖利全, 段书凯, 王丽丹. 基于Julia分形的多涡卷忆阻混沌系统[J]. 物理学报, 2018, 67(9): 090502. doi: 10.7498/aps.67.20172761XIAO Liquan, DUAN Shukai, and WANF Lidan. Julia fractal based multi-scroll memristive chaotic system[J]. Acta Physica Sinica, 2018, 67(9): 090502. doi: 10.7498/aps.67.20172761 闵富红, 王珠林, 王恩荣, 等. 新型忆阻器混沌电路及其在图像加密中的应用[J]. 电子与信息学报, 2016, 38(10): 2681–2688. doi: 10.11999/JEIT160178MIN Fuhong, WANG Zhulin, WANG Enrong, et al. New memristor chaotic circuit and its application to image encryption[J]. Journal of Electronics &Information Technology, 2016, 38(10): 2681–2688. doi: 10.11999/JEIT160178 BAO Bocheng, QIAN Hui, XU Quan, et al. Coexisting behaviors of asymmetric attractors in hyperbolic-type memristor based Hopfield neural network[J]. Frontiers in Computational Neuroscience, 2017, 11: article81, 1–14. doi: 10.3389/fncom.2017.00081 BAO Han, HU Aihuang, LIU Wenbo, et al. Hidden bursting firings and bifurcation mechanisms in memristive neuron model with threshold electromagnetic induction[J]. IEEE Transactions on Neural Networks and Learning Systems, 2020, 31(2): 502–511. doi: 10.1109/TNNLS.2019.2905137 RINZEL J. Bursting Oscillations in An Excitable Membrane Model[M]. SLEEMAN B D and JARVIS R J. Ordinary and Partial Differential Equations. Berlin, Gormany: Springer, 1985: 304-316. 李旭, 张正娣, 毕勤胜. 两时间尺度下非光滑广义蔡氏电路系统的簇发振荡机理[J]. 物理学报, 2013, 62(22): 220502. doi: 10.7498/aps.62.220502LI Xu, ZHANG Zhengdi, and BI Qinsheng. Mechanism of bursting oscillations in non-smooth generalized Chua’s circuit with two time scales[J]. Acta Physica Sinica, 2013, 62(22): 220502. doi: 10.7498/aps.62.220502 李芳苑, 陈墨, 武花干. 忆阻高通滤波电路准周期与混沌环面簇发振荡及慢通道效应[J]. 电子与信息学报, 2020, 42(4): 811–817. doi: 10.11999/JEIT190373LI Fangyuan, CHEN Mo, and WU Huagan. Quasi-periodic, chaotic-torus bursting oscillations and SlowPassage effect in memristive high-pass filter circuit[J]. Journal of Electronics &Information Technology, 2020, 42(4): 811–817. doi: 10.11999/JEIT190373 HAN Xiujing, BI Qinsheng, ZHANG Chun, et al. Delayed bifurcations to repetitive spiking and classification of delay-induced bursting[J]. International Journal of Bifurcation and Chaos, 2014, 24(7): 1450098. doi: 10.1142/s0218127414500989 KOVACIC I and BRENNAN M J. The Duffing Equation: Nonlinear Oscillators and Their Behaviour[M]. Chichester, West Sussex: John Wiley & Sons, 2011: 2–5. HAN Xiujing, ZHANG Yi, BI Qinsheng, et al. Two novel bursting patterns in the Duffing system with multiple-frequency slow parametric excitations[J]. Chaos: An Interdisciplinary Journal of Nonlinear Science, 2018, 28(4): 043111. doi: 10.1063/1.5012519 KENGNE J, TABEKOUENG Z N, and FOTSIN H B. Coexistence of multiple attractors and crisis route to chaos in autonomous third order Duffing-Holmes type chaotic oscillators[J]. Communications in Nonlinear Science and Numerical Simulation, 2016, 36: 29–44. doi: 10.1016/j.cnsns.2015.11.009 YU Yue, ZHANG Zhengdi, and BI Qinsheng. Multistability and fast-slow analysis for van der Pol-Duffing oscillator with varying exponential delay feedback factor[J]. Applied Mathematical Modelling, 2018, 57: 448–458. doi: 10.1016/j.apm.2018.01.010 HAN Xiujing and BI Qinsheng. Bursting oscillations in Duffing’s equation with slowly changing external forcing[J]. Communications in Nonlinear Science and Numerical Simulation, 2011, 16(10): 4146–4152. doi: 10.1016/j.cnsns.2011.02.021 SABARATHINAM S, VOLOS C K, and THAMILMARAN K. Implementation and study of the nonlinear dynamics of a memristor-based Duffing oscillator[J]. Nonlinear Dynamics, 2017, 87(1): 37–49. doi: 10.1007/s11071-016-3022-8 BODO B, FOUDA J S A E, MVOGO A, et al. Experimental hysteresis in memristor based Duffing oscillator[J]. Chaos, Solitons & Fractals, 2018, 115: 190–195. doi: 10.1016/j.chaos.2018.08.030 VARSHNEY V, SABARATHINAM S, PRASAD A, et al. Infinite number of hidden attractors in memristor-based autonomous duffing oscillator[J]. International Journal of Bifurcation and Chaos, 2018, 28(1): 1850013. doi: 10.1142/s021812741850013x ADHIKARI S P, SAH M P, KIM H, et al. Three fingerprints of memristor[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2013, 60(11): 3008–3021. doi: 10.1109/tcsi.2013.2256171 -
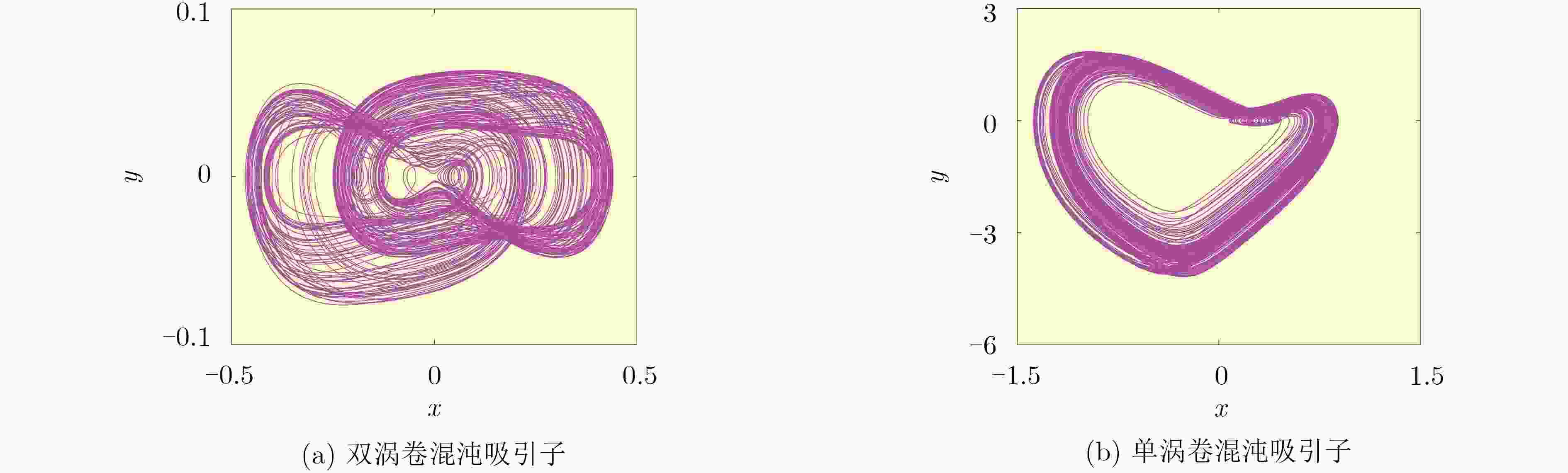
下载:
图(11)
计量
- 文章访问数: 2214
- HTML全文浏览量: 820
- PDF下载量: 131
- 被引次数: 0
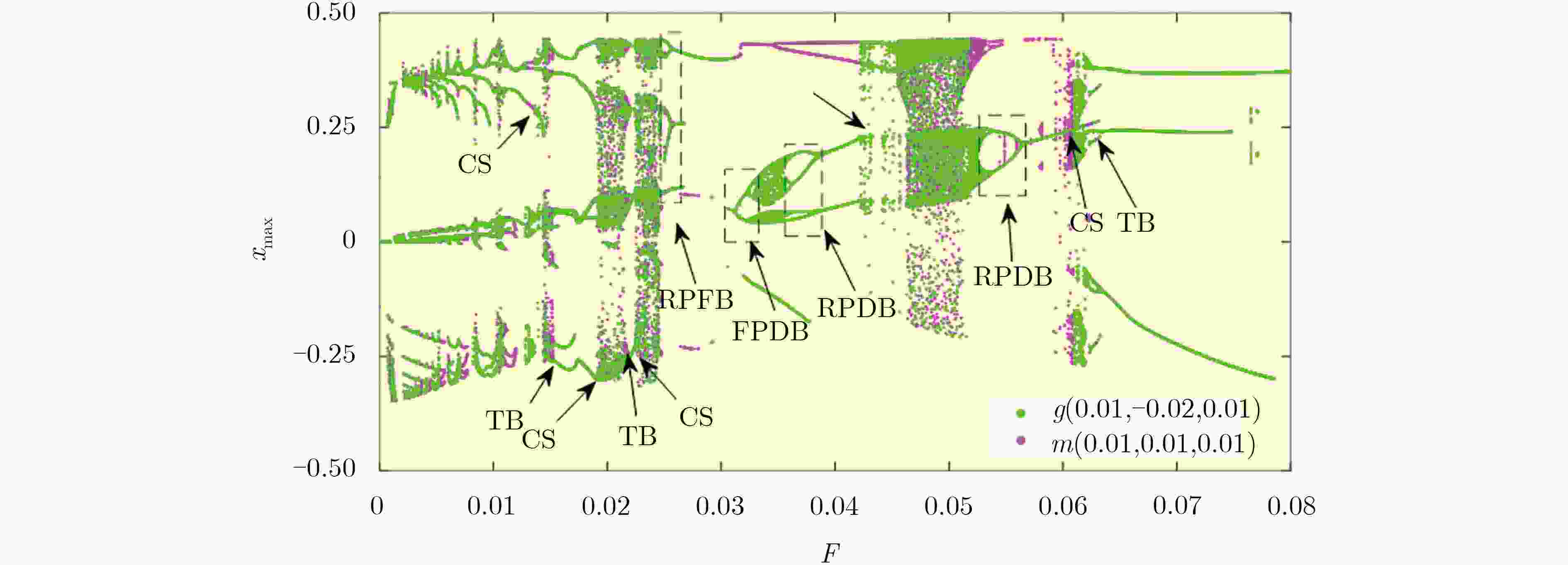
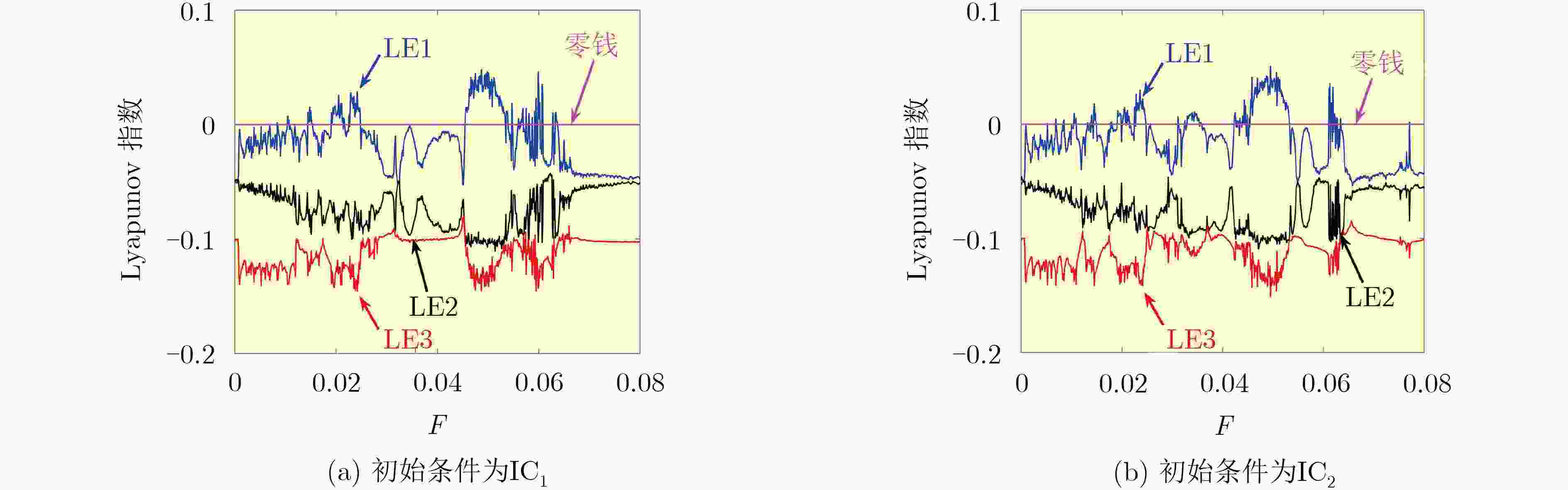
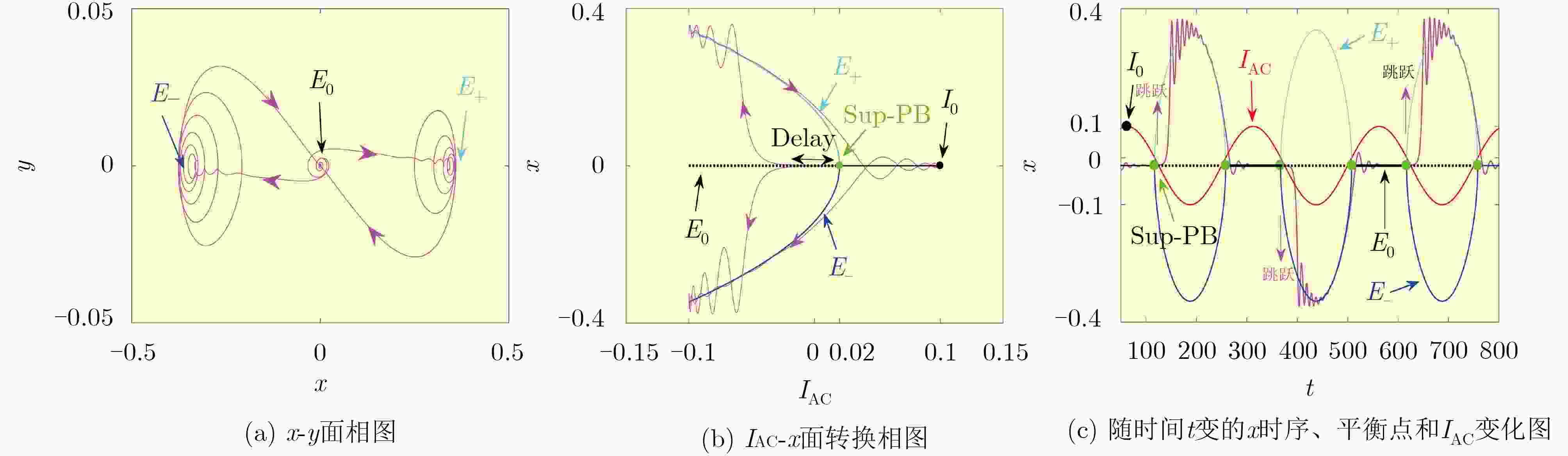
下载:
