Arbitrated Quantum Signature Scheme with Quantum Walks on Regular Graphs
-
摘要:
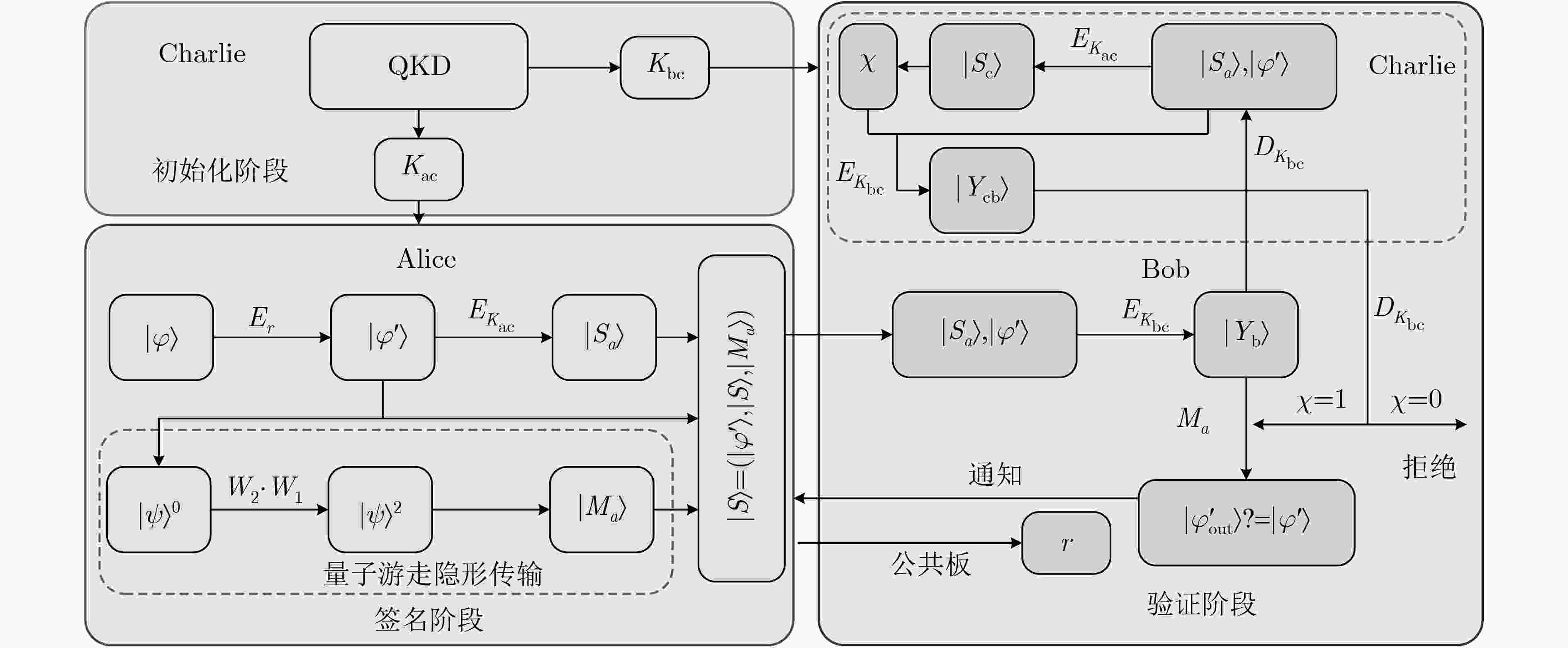
量子游走已经被提出可以用于瞬时地传输量子比特或多维量子态。根据量子游走的隐形传输模型,该文提出一种无需提前准备纠缠源的基于正则图上量子游走的仲裁量子签名算法。在初始化阶段,密钥是由量子密钥分发系统制备;在签名阶段,基于正则图上的量子游走隐形传输模型被用于转移信息副本密文从发送者到接收者。具体地,发送者编码要签名信息的密文在硬币态上,通过两步正则图上的量子游走,可以自动地产生用于量子隐形传输必须的纠缠态。发送者和接收者对制备的纠缠态的测量为签名生成和签名验证的凭据。在验证阶段,在仲裁的辅助下,验证者依照发送者的经典结果核实签名的有效性。此外,随机数和认证的公共板被引进阻止接收方在接收真正信息序列之前的存在性伪造攻击和否认攻击。安全性分析表明设计的算法满足签名者和接收者的不可抵赖以及任何人的不可伪造。讨论表明方案不能抗击发送者的抵赖攻击,相应的建议被给出。由于实验上已经证明量子游走可以在多个不同的物理系统上实现,因此该签名方案未来是可实现的。
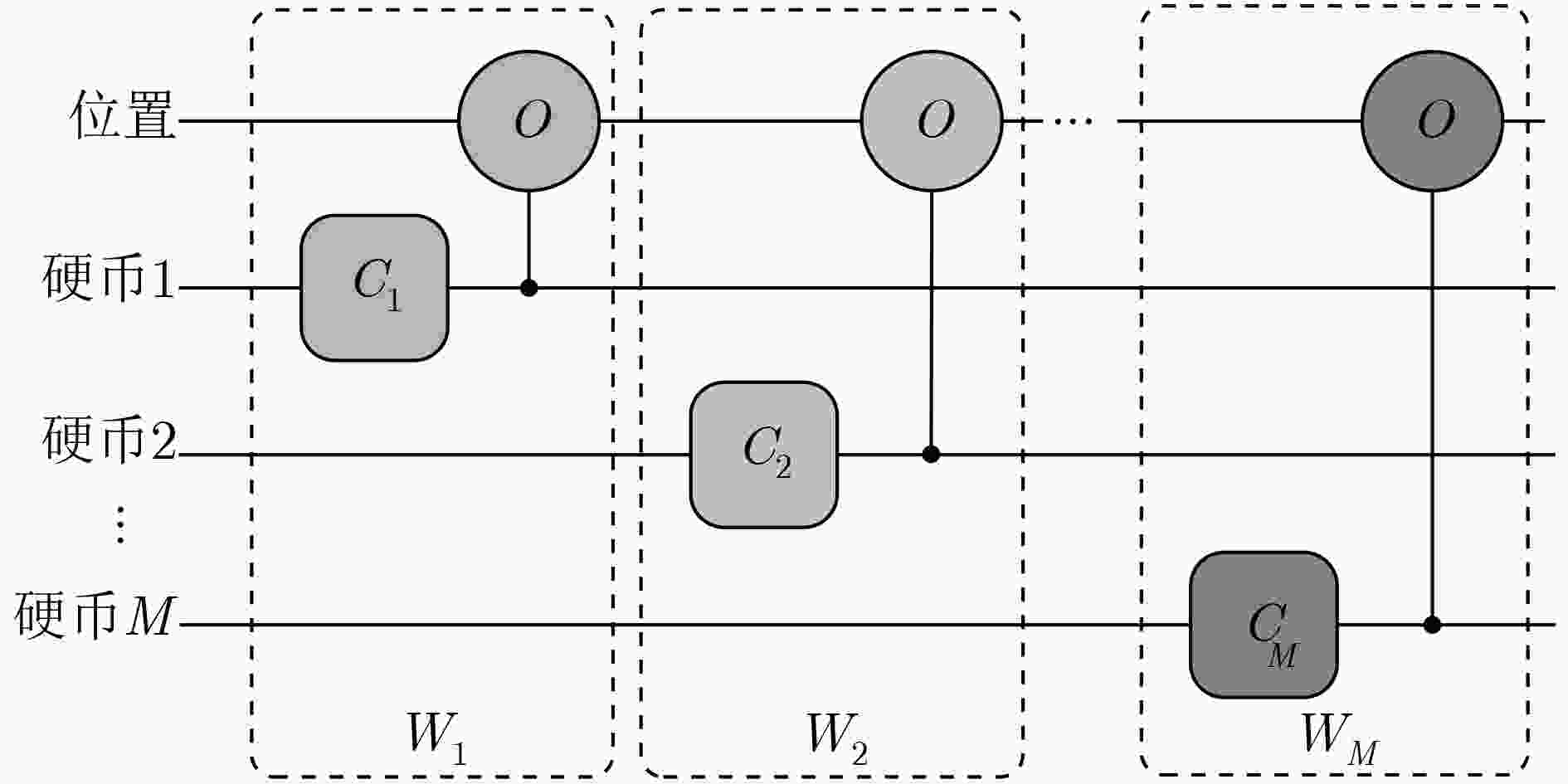
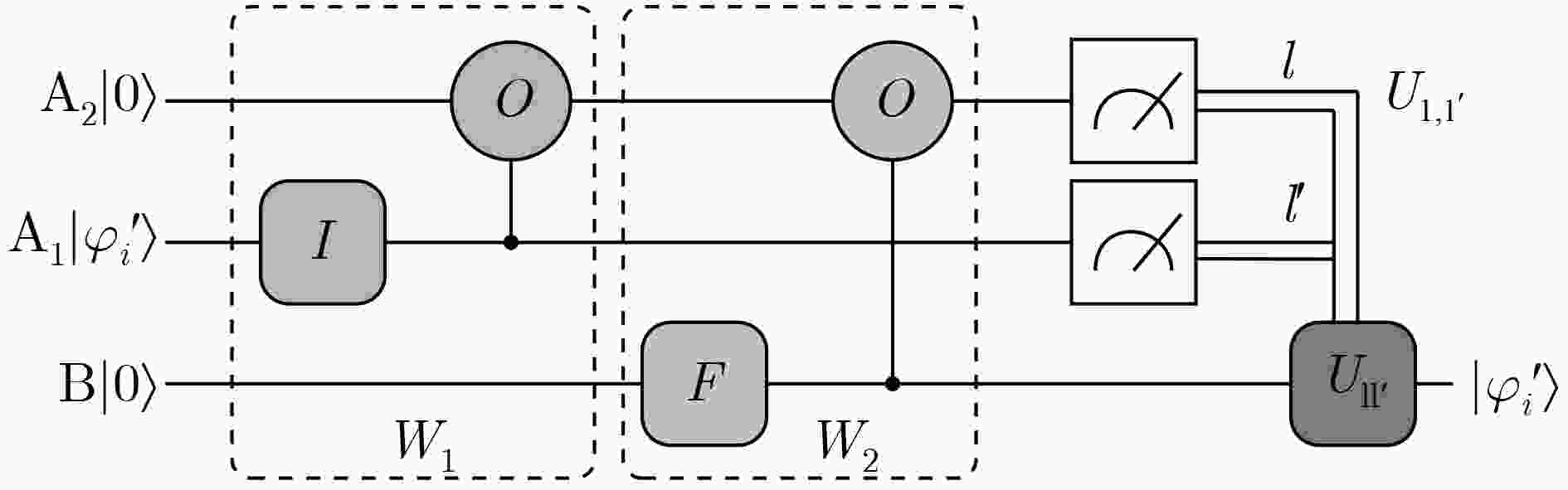
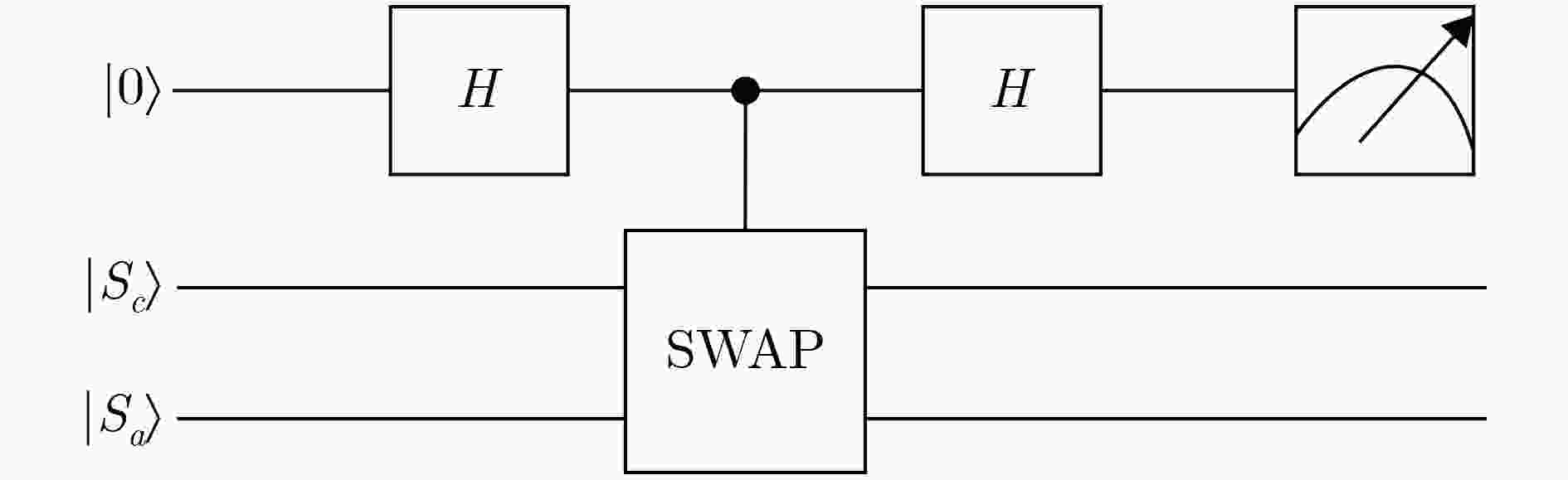
Abstract:Quantum walks are raised for teleporting qubit or qudit. Based on quantum walk teleportation, an arbitrated quantum signature scheme with quantum walks on regular graphs is suggested, in which the entanglement source does not need preparing ahead. In the initial phase, the secret keys are generated via quantum key distribution system. In the signing phase, the signature for the transmitted message is created by the signer. Teleportation of quantum walks on regular graphs is applied to teleporting encrypted message copy from the signer to the verifier. Concretely, the sender encodes the ciphertext of message copy on coin state. Then two-step quantum walks are performed on the initial system state engendering the necessary entangled state for quantum teleportation, which can be the basis of signature generation and verification. In the verifying phase, the verifier verifies the validity of the completed signature under the aid of an arbitrator. Additionally, the applications of random number and public board deter the verifier’s existential forgery and repudiation attacks before the verifier accepts the true message. Analyses show that the suggested arbitrated quantum signature algorithm satisfies the general two requirements, i.e., impossibility of disavowal from the signer and the verifier and impossibility of forgery from anyone. The discussions demonstrate that the scheme may not prevent disavowal attack from the signer and that the corresponding improvements are presented. The scheme may be realizable because quantum walks have experimentally proven to be implementable in different physical systems.
-
NIELSEN M A and CHUANG I. Quantum computation and quantum information[J]. American Journal of Physics, 2002, 70(5): 558–559. doi: 10.1119/1.1463744 SHOR P W. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer[J]. SIAM Review, 1999, 41(2): 303–332. doi: 10.1137/S0036144598347011 GROVER L K. Quantum mechanics helps in searching for a needle in a haystack[J]. Physical Review Letters, 1997, 79(2): 325–328. doi: 10.1103/PhysRevLett.79.325 GUO Ying, LIAO Qin, WANG Yijun, et al. Performance improvement of continuous-variable quantum key distribution with an entangled source in the middle via photon subtraction[J]. Physical Review A, 2017, 95(3): 032304. doi: 10.1103/PhysRevA.95.032304 ZHANG Zhaoyuan, SHI Ronghua, ZENG Guihua, et al. Coherent attacking continuous-variable quantum key distribution with entanglement in the middle[J]. Quantum Information Processing, 2018, 17(6): 1–18. doi: 10.1007/s11128-018-1903-0 MEIJER H and AKL S. Digital signature schemes for computer communication networks[J]. ACM SIGCOMM Computer Communication Review, 1981, 11(4): 37–41. doi: 10.1145/1013879.802657 ZENG Guihua and KEITEL C H. Arbitrated quantum-signature scheme[J]. Physical Review A, 2002, 65(4): 042312. doi: 10.1103/PhysRevA.65.042312 BARNUM H, CRÉPEAU C, GOTTESMAN D, et al. Authentication of quantum messages[C]. The 43rd Annual IEEE Symposium on Foundations of Computer Science, Vancouver, Canada, 2002: 449–458. doi: 10.1109/SFCS.2002.1181969. LI Qin, CHAN W H, and LONG Dongyang. Arbitrated quantum signature scheme using Bell states[J]. Physical Review A, 2009, 79(5): 054307. doi: 10.1103/PhysRevA.79.054307 ZOU Xiangfu and QIU Daowen. Security analysis and improvements of arbitrated quantum signature schemes[J]. Physical Review A, 2010, 82(4): 042325. doi: 10.1103/PhysRevA.82.042325 GAO Fei, QIN Sujuan, GUO Fenzhuo, et al. Cryptanalysis of the arbitrated quantum signature protocols[J]. Physical Review A, 2011, 84(2): 022344. doi: 10.1103/PhysRevA.84.022344 CHOI J W, CHANG K Y, and HONG D. Security problem on arbitrated quantum signature schemes[J]. Physical Review A, 2011, 84(6): 062330. doi: 10.1103/PhysRevA.84.062330 张骏, 吴吉义. 可证明安全高效的仲裁量子签名方案[J]. 北京邮电大学学报, 2013, 36(2): 113–116.ZHANG Jun and WU Jiyi. Provable secure efficient arbitrated quantum signature scheme[J]. Journal of Beijing University of Posts and Telecommunications, 2013, 36(2): 113–116. LI Fengguang and SHI Jianhong. An arbitrated quantum signature protocol based on the chained CNOT operations encryption[J]. Quantum Information Processing, 2015, 14(6): 2171–2181. doi: 10.1007/s1112 YANG Yuguang, LEI He, LIU Zhichao, et al. Arbitrated quantum signature scheme based on cluster states[J]. Quantum Information Processing, 2016, 15(6): 2487–2497. doi: 10.1007/s11128-016-1293-0 ZHANG Long, SUN Hongwei, ZHANG Kejia, et al. An improved arbitrated quantum signature protocol based on the key-controlled chained CNOT encryption[J]. Quantum Information Processing, 2017, 16(3): 1–15. doi: 10.1007/s11128-017-1531-0 ZHANG Yingying and ZENG Jiwen. An improved arbitrated quantum scheme with Bell states[J]. International Journal of Theoretical Physics, 2018, 57(4): 994–1003. doi: 10.1007/s10773-017-3632-z GUO Ying, FENG Yanyan, HUANG Dazu, et al. Arbitrated quantum signature scheme with continuous-variable coherent states[J]. International Journal of Theoretical Physics, 2016, 55(4): 2290–2302. doi: 10.1007/s10773-015-2867-9 FENG Yanyan, SHI Ronghua, and GUO Ying. Arbitrated quantum signature scheme with continuous-variable squeezed vacuum states[J]. Chinese Physics B, 2018, 27(2): 020302. doi: 10.1088/1674-1056/27/2/020302 LOU Xiaoping, LONG Hu, TANG Wensheng, et al. Continuous-variable arbitrated quantum signature based on dense coding and teleportation[J]. IEEE Access, 2019, 7: 85719–85726. doi: 10.1109/ACCESS.2019.2925635 BENNETT C H, BRASSARD G, CRÉPEAU C, et al. Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels[J]. Physical Review Letters, 1993, 70(13): 1895–1899. doi: 10.1103/PhysRevLett.70.1895 REN Lijie, HE Guangqiang, and ZENG Guihua. Universal teleportation via continuous-variable graph states[J]. Physical Review A, 2008, 78(4): 042302. doi: 10.1103/PhysRevA.78.042302 AHARONOV Y, DAVIDOVICH L, and ZAGURY N. Quantum random walks[J]. Physical Review A, 1993, 48(2): 1687–1690. doi: 10.1103/PhysRevA.48.1687 MEYER D A. From quantum cellular automata to quantum lattice gases[J]. Journal of Statistical Physics, 1996, 85(5/6): 551–574. doi: 10.1007/BF02199356 FARHI E and GUTMANN S. Quantum computation and decision trees[J]. Physical Review A, 1998, 58(2): 915–928. doi: 10.1103/PhysRevA.58.915 CHILDS A M and Goldstone J. Spatial search by quantum walk[J]. Physical Review A, 2004, 70(2): 022314. doi: 10.1103/PhysRevA.70.022314 AARONSON S and SHI Yaoyun. Quantum lower bounds for the collision and the element distinctness problems[J]. Journal of the ACM, 2004, 51(4): 595–605. doi: 10.1145/1008731.1008735 DOUGLAS B L and WANG J B. A classical approach to the graph isomorphism problem using quantum walks[J]. Journal of Physics A: Mathematical and Theoretical, 2008, 41(7): 075303. doi: 10.1088/1751-8113/41/7/075303 DU Jiangfeng, LI Hui, XU Xiaodong, et al. Experimental implementation of the quantum random-walk algorithm[J]. Physical Review A, 2003, 67(4): 042316. doi: 10.1103/PhysRevA.67.042316 SCHMITZ H, MATJESCHK R, SCHNEIDER C, et al. Quantum walk of a trapped ion in phase space[J]. Physical Review Letter, 2009, 103(9): 090504. doi: 10.1103/PhysRevLett.103.090504 PERUZZO A, LOBINO M, MATTHEWS J C F, et al. Quantum walks of correlated photons[J]. Science, 2010, 329(5998): 1500–1503. doi: 10.1126/science.1193515 WANG Yu, SHANG Yun, and XUE Peng. Generalized teleportation by quantum walks[J]. Quantum Information Processing, 2017, 16(9): 1–13. doi: 10.1007/s11128-017-1675-y SHANG Yun, WANG Yu, LI Meng, et al. Quantum communication protocols by quantum walks with two coins[J]. EPL (Europhysics Letters) , 2019, 124(6): 60009. doi: 10.1209/0295-5075/124/60009 AHARONOV D, AMBAINIS A, KEMPE J, et al. Quantum walks on graphs[C]. The 33rd Annual ACM Symposium on Theory of Computing, Hersonissos, Greece, 2001: 50–59. doi: 10.1145/380752.380758. BRUN T A, CARTERET H A, and AMBAINIS A. Quantum walks driven by many coins[J]. Physical Review A, 2003, 67(5): 052317. doi: 10.1103/PhysRevA.67.052317 BUHRMAN H, CLEVE R, WATROUS J, et al. Quantum fingerprinting[J]. Physical Review Letters, 2001, 87(16): 167902. doi: 10.1103/PhysRevLett.87.167902 PÉREZ E, CURTY M, SANTOS D J, et al. Quantum authentication with unitary coding sets[J]. Journal of Modern Optics, 2003, 50(6/7): 1035–1047. doi: 10.1080/09500340308234550 -





 下载:
下载:




 下载:
下载:
