An Improved Fuzzy Clustering Method for Interval Uncertain Data
-
摘要:
针对区间型不确定数据的特点,该文提出一种改进的模糊C均值聚类算法(IU-IFCM)。首先对区间型数据进行特征变换,由p维特征映射成由2p维特征组成的实数据,然后考虑区间中值与区间大小关系,设计一种样本距离计算方法,通过模糊C均值实现对区间型样本聚类。理论分析与对比实验表明,该算法的划分系数(PC)及正确等级(CR)值比其它方法平均提高10%以上,表明有更好的聚类精度,对当前大数据环境下不确定数据的分类提供了一种新的解决方案。
Abstract:An Improved Fuzzy C-Means clustering algorithm (IU-IFCM) is proposed in this study in accordance with the characteristics of Interval Uncertain data. First, the interval data is transformed into real data composed of 2p dimension feature, which is mapped from that of p dimension feature. Second, a method for calculating sample distance, which realizes the interval sample clustering by fuzzy c-mean algorithm, is designed while considering the relationship between interval median value and interval size. Theoretical analysis and comparison experiments show that the presented algorithm surpaes the compared algorithms by more than 10% on average in terms of the Partition Coefficient (PC) and Correct Rank(CR) value. These results indicate that the algorithm presents in this study has better clustering accuracy and provides a new solution for the classification of uncertain data in current big data environments.
-
Key words:
- Interval data /
- Fuzzy C-means /
- Impact factor /
- Feature transformation
-
表 1 Fat_Oil数据集
样本 比重(g/cm3) 冰点(°C) io值 sa值 亚麻油 [0.930 0.935] [–27 –8] [170 204] [118 196] 紫苏油 [0.930 0.937] [–5 –4] [192 208] [188 197] 棉籽油 [0.916 0.918] [–6 –1] [99 113] [189 198] 芝麻油 [0.920 0.926] [–6 –4] [104 116] [187 193] 山茶油 [0.916 0.917] [–21 –15] [80 82] [189 193] 橄榄油 [0.914 0.919] [0 6] [79 90] [187 196] 牛油 [0.860 0.870] [30 38] [40 48] [190 199] 猪油 [0.858 0.864] [22 32] [53 77] [190 202] 表 2 4种算法对Fish数据集的分类结果
腐屑性 肉食性 杂食性 草食性 先验分类 1 2 3 4 5 6 7 8 9 10 11 12 E_FCM 1 2 5 4 6 3 7 10 8 9 11 12 M_FCM 1 3 4 6 10 11 2 8 5 7 9 12 D_FCM 1 2 4 5 6 8 9 3 10 11 7 12 IU_IFCM 1 2 3 4 6 7 8 5 9 10 11 12 表 3 人工数据集
参数 类1 类2 类3 ${m_1}$ 28 60 45 ${m_2}$ 22 30 38 $\sigma _1^2$ 100 9 9 $\sigma _2^2$ 9 144 9 -
JIANG Bin, PEI Jian, TAO Yufei, et al. Clustering uncertain data based on probability distribution similarity[J]. IEEE Transactions on Knowledge and Data Engineering, 2013, 25(4): 751–763. doi: 10.1109/TKDE.2011.221 GULLO F and TAGARELLI A. Uncertain centroid based partitional clustering of uncertain data[J]. Proceedings of the VLDB Endowment, 2012, 5(7): 610–621. doi: 10.14778/2180912.2180914 DALLACHIESA M, JACQUES-SILVA G, GEDIK B, et al. Sliding windows over uncertain data streams[J]. Knowledge and Information Systems, 2015, 45(1): 159–190. doi: 10.1007/s10115-014-0804-5 彭宇, 罗清华, 彭喜元. UIDK-means: 多维不确定性测量数据聚类算法[J]. 仪器仪表学报, 2011, 32(6): 1201–1207. doi: 10.19650/j.cnki.cjsi.2011.06.001PENG Yu, LUO Qinghua, and PENG Xiyuan. UIDK-means: A Multi-dimensional uncertain measurement data clustering algorithm[J]. Chinese Journal of Scientific Instrument, 2011, 32(6): 1201–1207. doi: 10.19650/j.cnki.cjsi.2011.06.001 BAO Chaozheng, PENG Hongming, HE Di, et al. Adaptive fuzzy c-means clustering algorithm for interval data type based on interval-dividing technique[J]. Pattern Analysis and Applications, 2018, 21(3): 803–812. doi: 10.1007/s10044-017-0663-2 D’URSO P, MASSARI R, DE GIOVANNI L, et al. Exponential distance-based fuzzy clustering for interval-valued data[J]. Fuzzy Optimization and Decision Making, 2017, 16(1): 51–70. doi: 10.1007/s10700-016-9238-8 BRITO P, SILVA A P D, and DIAS J G. Probabilistic clustering of interval data[J]. Intelligent Data Analysis, 2015, 19(2): 293–313. doi: 10.3233/IDA-150718 HAMDAN H. Maximum likelihood estimation from interval-valued data. Application to fuzzy clustering[C]. The 13th International Conference on Theory and Application of Fuzzy Systems and Soft Computing -ICAFS-2018. Istanbul, Turkey, 2019: 3–10. doi: 10.1007/978-3-030-04164-9_3. 谢志伟, 王志明. 一种区间型数据的自适应模糊C均值聚类算法[J]. 计算机工程与应用, 2012, 48(17): 193–198, 237. doi: 10.3778/j.issn.1002-8331.2012.17.038XIE Zhiwei and WANG Zhiming. Self-adapting fuzzy c means clustering algorithm for interval data[J]. Computer Engineering and Applications, 2012, 48(17): 193–198, 237. doi: 10.3778/j.issn.1002-8331.2012.17.038 GAO Xinbo, JI Hongbing, and XIE Weixin. A novel FCM clustering algorithm for interval-valued data and fuzzy-valued data[C]. The 5th International Conference on Signal Processing Proceedings. The 16th World Computer Congress 2000, Beijing, China, 2000: 1551–1555. doi: 10.1109/ICOSP.2000.893395. MACIEL L, BALLINI R, GOMIDE F, et al. Participatory learning fuzzy clustering for interval-valued data[C]. The 16th International Conference on Information Processing and Management of Uncertainty in Knowledge-Based Systems, Eindhoven, The Netherlands, 2016: 687–698. doi: 10.1007/978-3-319-40596-4_57. 兰蓉. 模糊信息距离及其若干应用[D]. [博士论文], 西安电子科技大学, 2013: 61–73.LAN Rong. Fuzzy information distances and their some applications[D]. [Ph.D. dissertation], Xidian University, 2013: 61–73. 金萍, 宗瑜, 屈世超, 等. 面向不确定数据的近似骨架启发式聚类算法[J]. 南京大学学报: 自然科学, 2015, 51(1): 197–205. doi: 10.13232/j.cnki.jnju.2015.01.027JIN Ping, ZONG Yu, QU Shichao, et al. Approximate backbone guided heuristic clustering algorithm for uncertain data[J]. Journal of Nanjing University:Natural Sciences, 2015, 51(1): 197–205. doi: 10.13232/j.cnki.jnju.2015.01.027 魏方圆, 黄德才. 基于区间数的多维不确定性数据UID-DBSCAN聚类算法[J]. 计算机科学, 2017, 44(11A): 442–447. doi: 10.11896/j.issn.1002-137X.2017.11A.094WEI Fangyuan and HUANG Decai. UID-DBSCAN clustering algorithm of multi-dimensional uncertain data based on interval number[J]. Computer Science, 2017, 44(11A): 442–447. doi: 10.11896/j.issn.1002-137X.2017.11A.094 ZHANG Qin, FANG Zhigeng, LIU Sifeng, et al. On variable weight clustering model of generalized interval grey numbers for multiple uncertain data[J]. Journal of Grey System, 2019, 31(1): 84–99. 陆亿红, 任胜亮. 基于区间数的不确定数据流2κ近邻聚类算法[J]. 浙江工业大学学报, 2018, 46(3): 321–326. doi: 10.3969/j.issn.1006-4303.2018.03.015LU Yihong and REN Shengliang. The clustering algorithm of uncertain data stream 2κ-near neighbors based on interval number[J]. Journal of Zhejiang University of Technology, 2018, 46(3): 321–326. doi: 10.3969/j.issn.1006-4303.2018.03.015 张新猛, 蒋盛益. 一种基于相似度概率的不确定分类数据聚类算法[J]. 山东大学学报: 工学版, 2011, 41(3): 12–16.ZHANG Xinmeng and JIANG Shengyi. An algorithm for clustering uncertain categorical data based on similarity probability[J]. Journal of Shandong University:Engineering Science, 2011, 41(3): 12–16. TRAN L and DUCKSTEIN L. Comparison of fuzzy numbers using a fuzzy distance measure[J]. Fuzzy Sets and Systems, 2002, 130(3): 331–341. doi: 10.1016/s0165-0114(01)00195-6 -





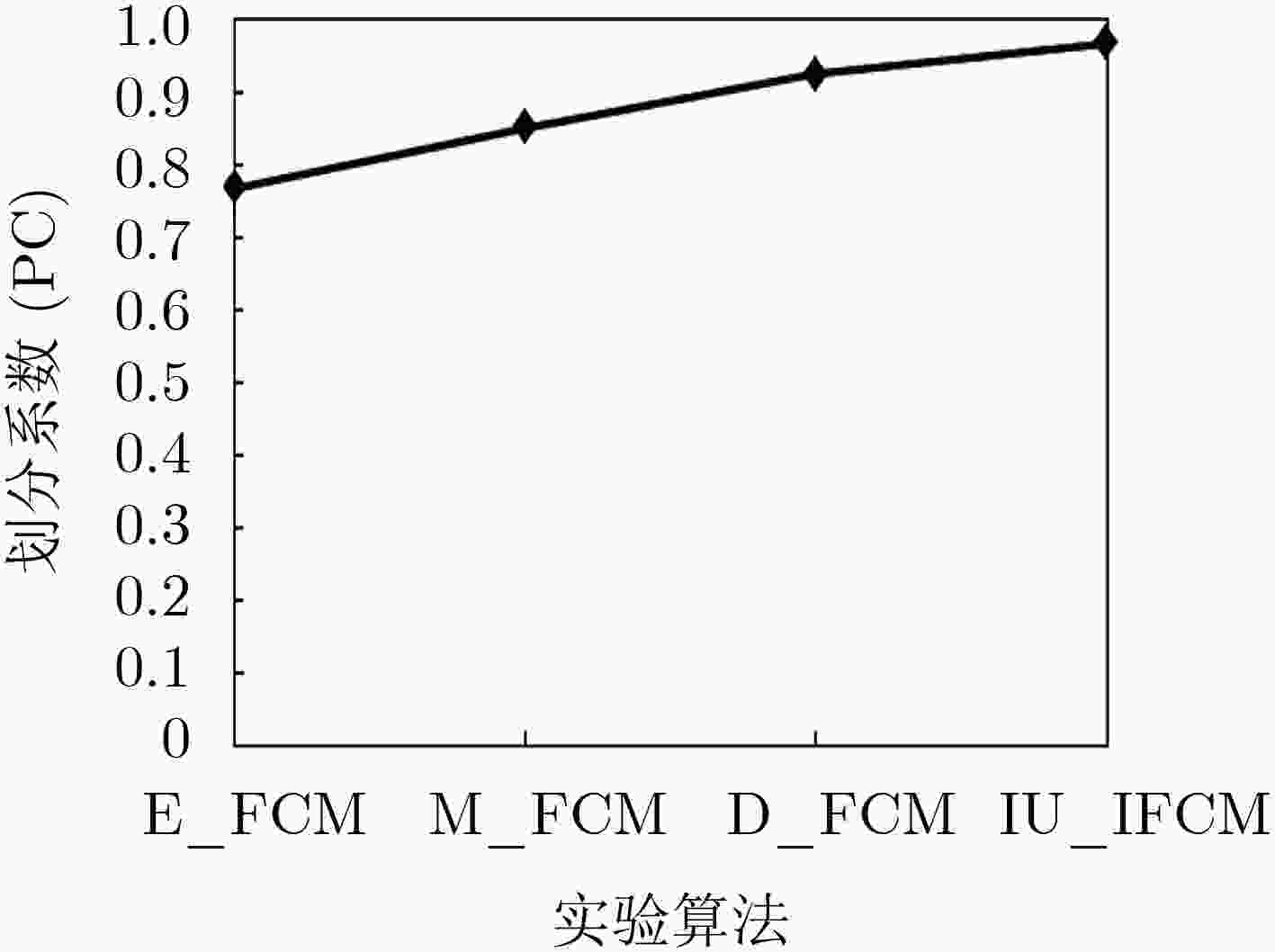
 下载:
下载:
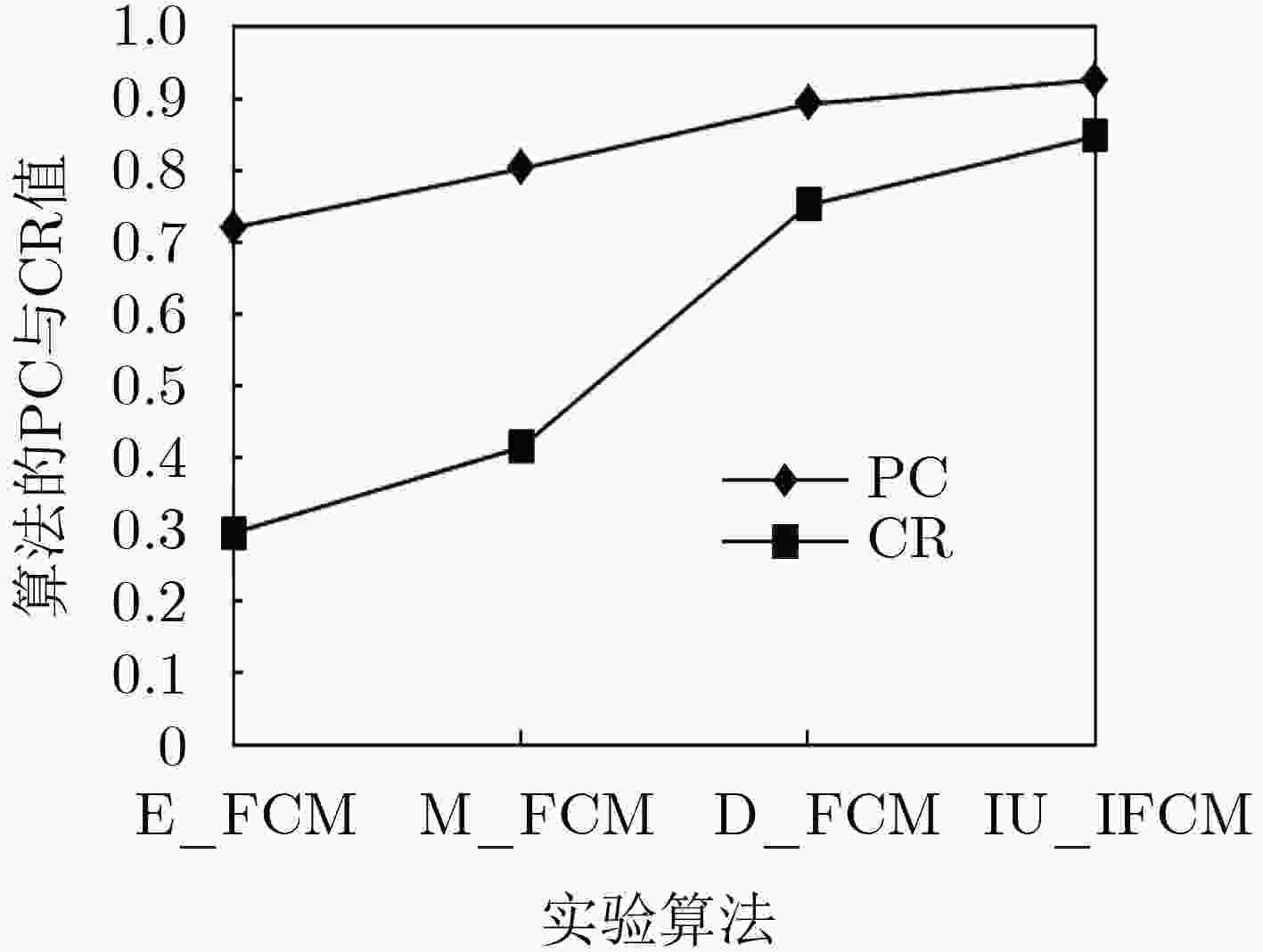
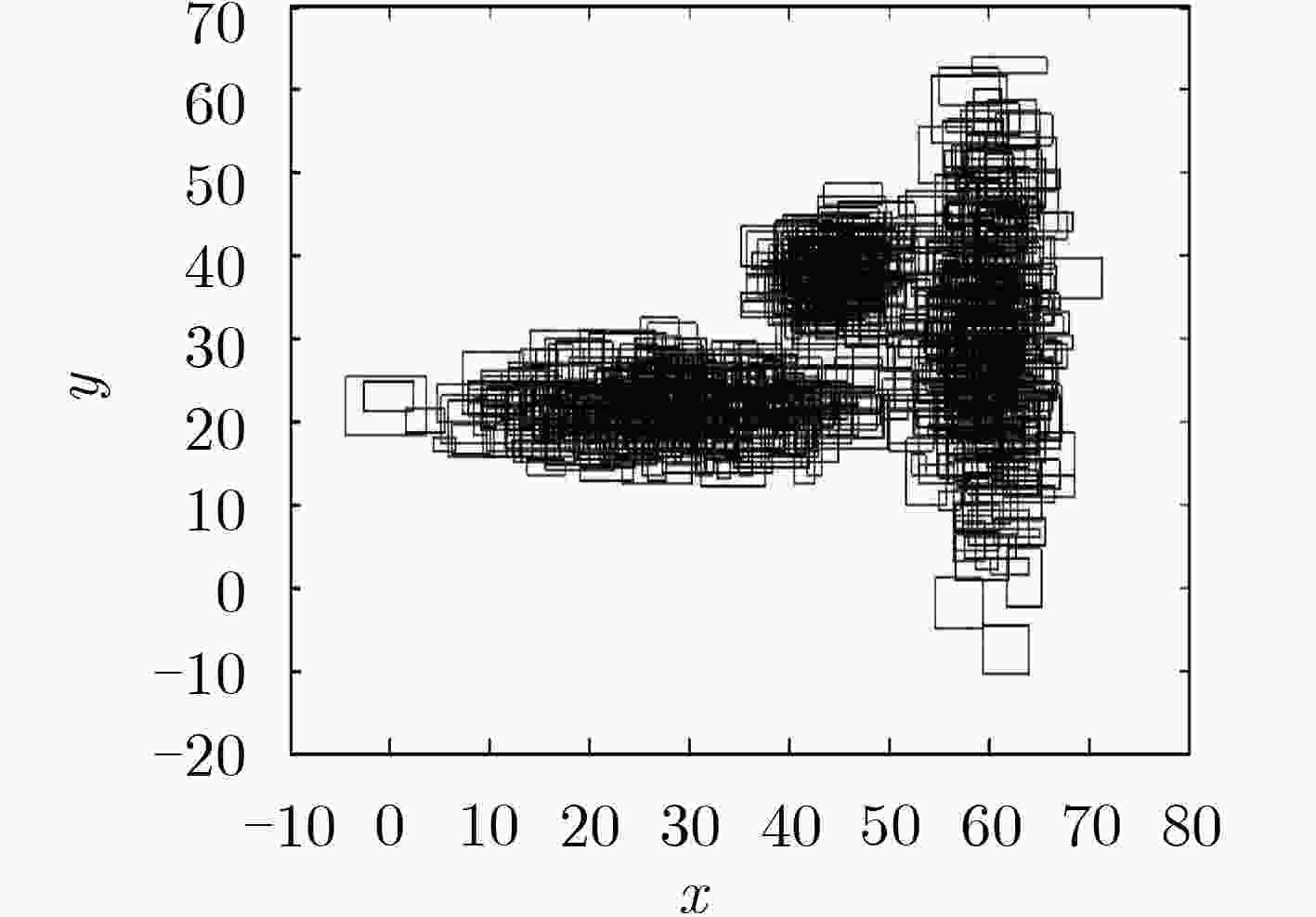
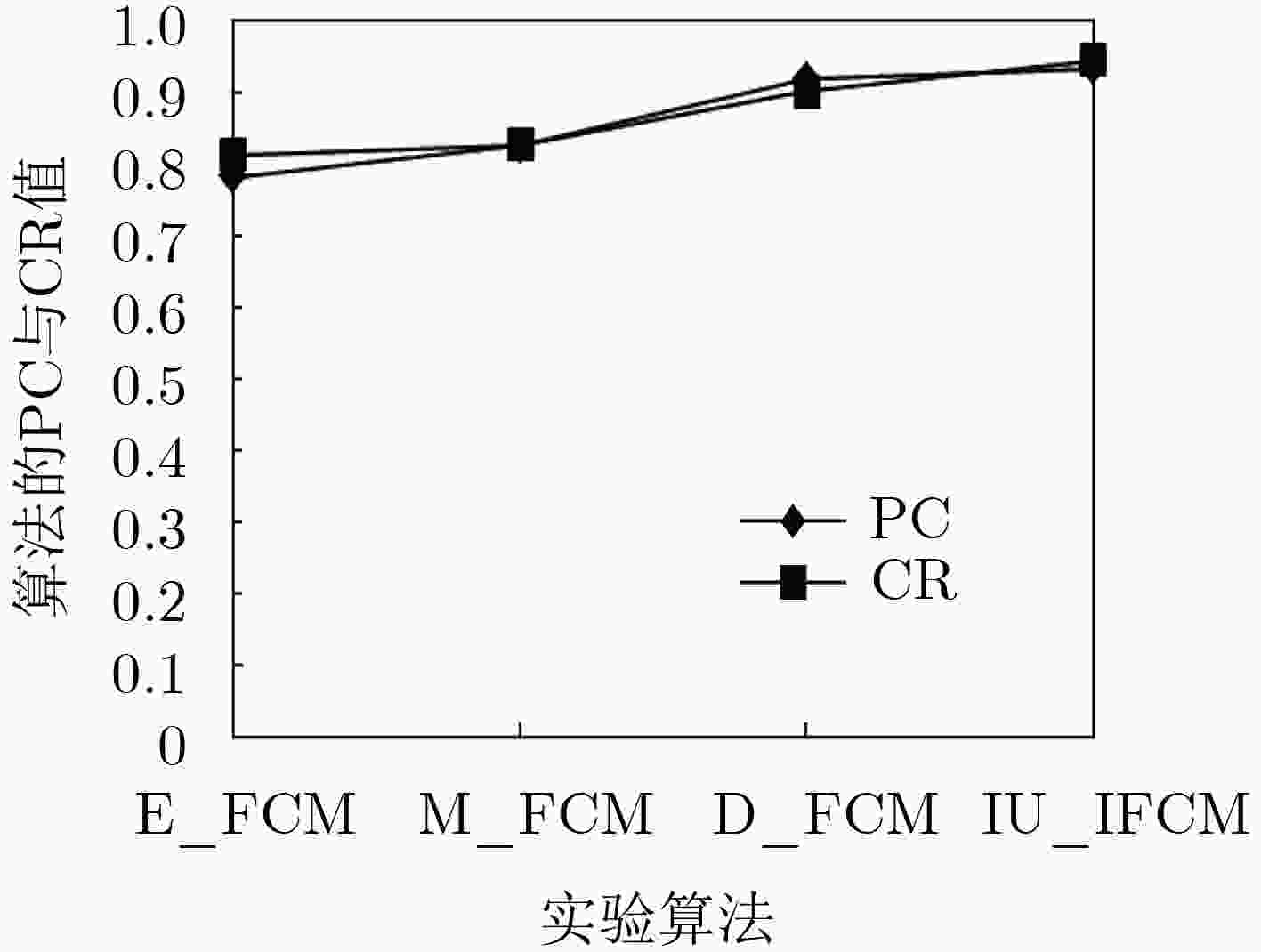


 下载:
下载:
