基于分解和支配关系的超多目标进化算法

赵辉; 王天龙; 刘衍舟; 黄橙; 张天骐

doi:10.11999/JEIT190589

基于分解和支配关系的超多目标进化算法

doi: 10.11999/JEIT190589

1.
重庆邮电大学通信与信息工程学院重庆 400065
2.
信号与信息处理重庆市重点实验室重庆 400065

基金项目: 国家自然科学基金(61671095)

详细信息

作者简介:
赵辉：女，1980年生，教授，博士生导师，研究方向为深空光通信、信号理论与信息处理、信号与图像处理

王天龙：男，1994年生，硕士，研究方向为信号与图像处理、进化计算、多目标优化

刘衍舟：男，1994年生，硕士，研究方向为信号与图像处理

黄橙：男，1993年生，硕士，研究方向为信号与图像处理

张天骐：男，1971年生，教授，博士生导师，研究方向为无线通信的智能信号处理、通信抗干扰和信息对抗

通讯作者:
赵辉　zhaohui@cqupt.edu.cn

中图分类号: TP391.4
计量
- 文章访问数: 3296
- HTML全文浏览量: 1077
- PDF下载量: 91
- 被引次数: 0
出版历程
- 收稿日期: 2019-08-05
- 修回日期: 2020-02-13
- 网络出版日期: 2020-03-25
- 刊出日期: 2020-08-18

Decomposition and Dominance Relation Based Many-objective Evolutionary Algorithm

1.
School of Communication and Information Engineering, Chongqing University of Posts and Telecommunications, Chongqing 400065, China
2.
Chongqing Key Laboratory of Signal and Information Processing, Chongqing 400065, China

Funds: The National Natural Science Foundation of China (61671095)

摘要

摘要:
近年来，超多目标优化问题(MaOPs)成为了进化计算领域的研究热点。然而，在处理各种优化问题中，如何有效地平衡收敛性和多样性仍是一个难题。为了解决上述的问题，该文提出了一种基于分解和支配关系的超多目标进化算法(DdrEA)。首先利用权重向量把整个种群分解为一组子种群，这些子种群将进行协同优化；然后利用角度和角度支配关系计算子种群内每个解的值；最后根据适应度值进行精英选择，即在每个子空间内选取适应度值最小的解作为精英解进入下一代。DdrEA通过与当前较优的NSGA-II/AD, RVEA, MOMBI-II等多个超多目标进化算法进行实验对比，实验结果表明该文算法性能明显优于对比算法，能够有效平衡种群的收敛性和多样性。
- 超多目标优化 /
- 分解 /
- 支配关系 /
- 进化算法
Abstract:
In recent year, the Many-objective Optimization Problems (MaOPs) have become an increasingly hot research area in evolutionary computation. However, it is still a difficult problem to achieve a good balance between convergence and diversity on solving various kinds of MaOPs. To alleviate this issue mentioned above, a Decomposition and dominance relation based many-objective Evolutionary Algorithm(DdrEA) is proposed in this paper. Firstly, the population is decomposed into numbers of sub-populations by using a set of uniform weight vectors, in which they are optimized in a cooperative manner. Then, the fitness value of solution in each sub-population is calculated by angle dominance relation and angle. Finally, elite selection strategy is performed according to its corresponding fitness value. That is, in each subspace, the solution with the smallest fitness value is selected as the elite solution to enter the next generation. Comparing with several high-dimensional and multi-objective evolutionary algorithms (NSGA-II/AD, RVEA, MOMBI-II), the experimental results show that the performance of the proposed algorithm DdrEA is better than that of the comparison algorithm, and the convergence and diversity of the population can be effectively balanced.
- Many-objective optimization /
- Decomposition /
- Dominance relation /
- Evolutionary algorithm

HTML全文

图 1 两个目标下的角度支配准则

下载: 全尺寸图片幻灯片

图 2 各算法在15目标WFG1问题上获得的结果

下载: 全尺寸图片幻灯片

图 3 各算法在10目标WFG9问题上获得的结果

下载: 全尺寸图片幻灯片

表 1 DdrEA算法框架

输入: N (种群规模)
输出: P (最终种群)
(1) ${ V} = \operatorname{Uniform\;Reference\;Vector} (N)$;
(2) $P = \operatorname{RandomInitialize} (N)$;
(3) 　while 终止条件未满足 do
(4) 　　${\rm{Pool} } = \operatorname{Bianry\;Tournament} (P)$;
(5) 　　$O = \operatorname{Variation} ({\rm{Pool}})$;
(6) 　　$P = \operatorname{Environmental\;Selection} (P \cup O,V,N)$;
(7) 　end while

下载: 导出CSV

表 2 环境选择算法框架

输入: P (合并后的种群), V (参考向量);
输出: Q (下一代种群);
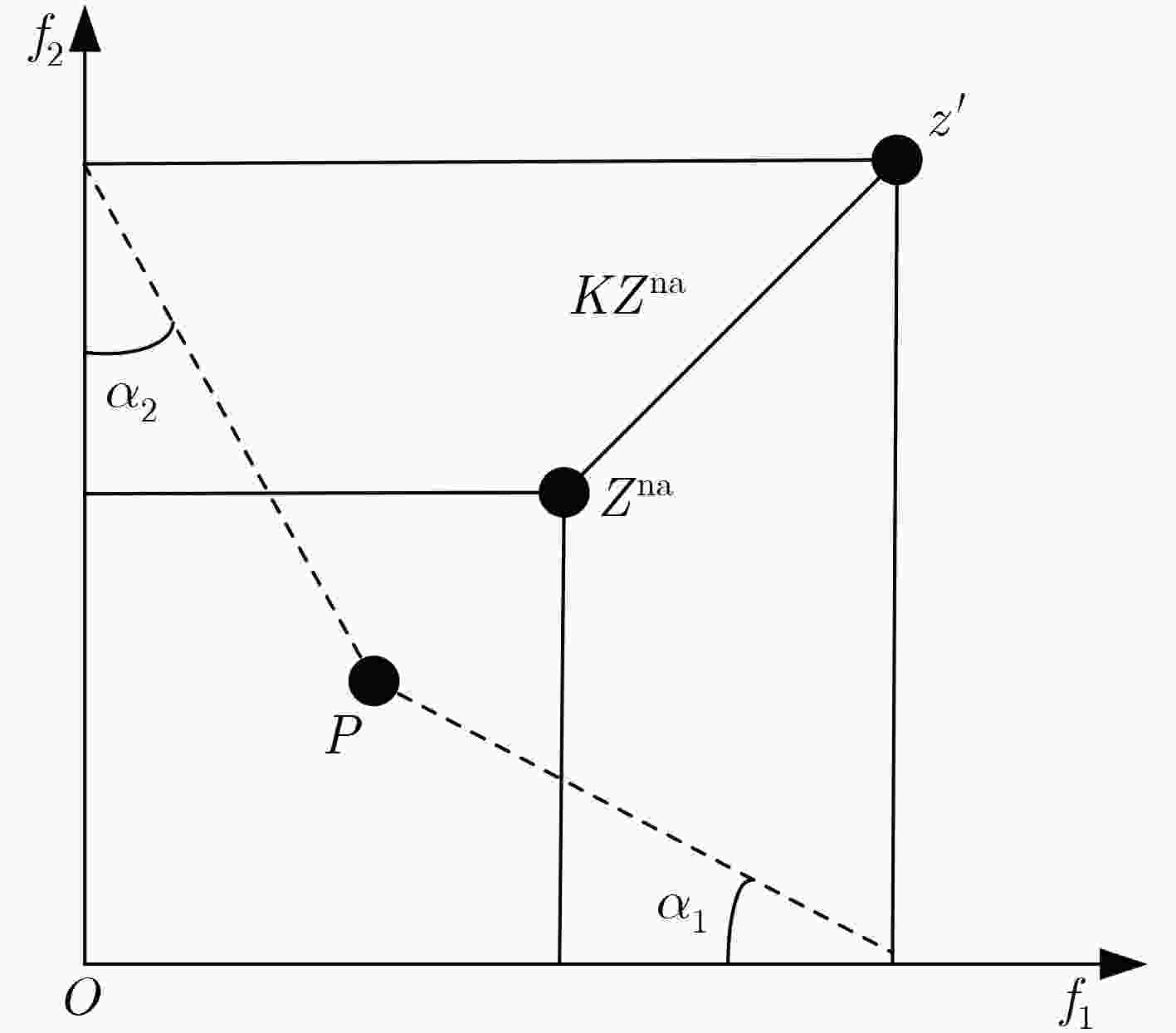
(1) /目标值标准化/ 　(2) ${f_i}\;(p) = \dfrac{{{f_i}(p) - z_i^{{\rm{id}}}}}{{z_i^{{\rm{na}}} - z_i^{{\rm{id}}}}},\forall p \in P$;
(3) /种群分解/
(4) for $i = 1\;{\rm{to }}\left\| P \right\|$ do
(5) 　for $j = 1\;{\rm{to }}N$ do 　(6) 　　${\theta _{i,j} } = \arccos \dfrac{ { {f_i}\;(p) \cdot {v_j} } }{ {\left\\| { {f_i}\;(p)} \right\\|} }$;
(7) 　end for
(8) end for
(9) for $i = 1\;{\rm{to }}\left\| P \right\|$ do
(10) 　　$r = \arg \min {\theta _{i,j}},j \in \{ 1,2, ··· ,N\} $;
(11) 　　${\overline P _k} = {\overline P _k} \cup \{ {I_r}\} $;
(12) end for
(13) /精英选择/
(14) 非支配排序获得每个解的AD等级;
(15) for $i = 1\;{\rm{to }}N$ do
(16) 　for $j = 1\;{\rm{to } }\left\| { { { {\overline P}_k} } } \right\|$ do
(17) 　　${\rm{fi}}{{\rm{t}}_{i,j}} = F_i^p + {\theta _{i,j}}$;
(18) 　end for
(19) end for
(20) for $i = 1\;{\rm{to }}N$ do
(21) 　$r = \arg \min {\rm{fi}}{{\rm{t}}_{i,j}}$
(22) 　$Q = Q \cup \{ {I_r}\} $
(23) end for

下载: 导出CSV

表 3 各算法在WFG测试集上独立运行30次的HV均值和标准差

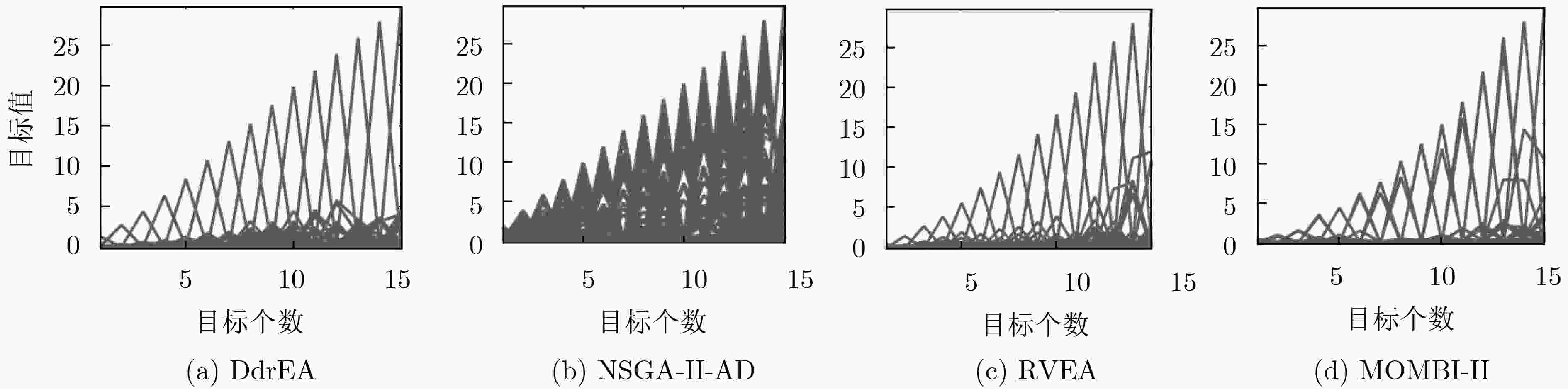
测试问题	M	DdrEA	NSGA-II/AD	RVEA	MOMBI-II
WFG1	5	9.7500e-1 (3.88e-3)	9.7759e-1 (1.72e-3) +	9.9722e-1 (5.54e-4) +	9.4668e-1 (5.46e-2) =
	10	9.9821e-1 (4.94e-4)	9.9849e-1 (1.57e-4) +	9.9768e-1 (5.30e-4) –	9.9990e-1 (6.65e-5) +
	15	9.9960e-1 (2.23e-4)	9.9977e-1 (5.94e-5) +	9.9546e-1 (1.65e-2) –	9.9900e-1 (9.15e-4) –
WFG2	5	9.5980e-1 (4.39e-3)	9.8390e-1 (6.84e-4) +	9.9385e-1 (1.19e-3) +	9.9432e-1 (2.64e-3) +
	10	9.9548e-1 (1.94e-3)	9.9819e-1 (3.42e-4) +	9.8944e-1 (2.64e-3) –	9.9459e-1 (4.80e-3) =
	15	9.9516e-1 (3.28e-3)	9.9854e-1 (4.21e-4) +	9.7143e-1 (6.37e-3) –	9.4784e-1 (4.42e-2) –
WFG3	5	2.1343e-1 (1.95e-2)	2.4953e-1 (4.42e-3) +	1.5392e-1 (2.34e-2) –	9.1612e-2 (1.14e-3) –
	10	9.2805e-2 (1.72e-2)	7.7407e-2 (1.47e-2) –	0.0000e+0 (0.00e+0) –	8.8033e-2 (1.38e-2) =
	15	8.3502e-4 (3.18e-3)	5.6841e-4 (2.97e-3) =	0.0000e+0 (0.00e+0) =	0.0000e+0 (0.00e+0) =
WFG4	5	7.9321e-1 (6.31e-4)	6.4860e-1 (1.20e-3) –	7.9120e-1 (6.98e-4) –	7.9039e-1 (7.50e-3) =
	10	9.6871e-1 (4.54e-4)	8.3306e-1 (1.02e-3) –	9.5997e-1 (2.21e-3) –	9.2583e-1 (5.33e-2) –
	15	9.8842e-1 (4.27e-3)	9.0197e-1 (2.24e-3) –	9.7572e-1 (3.32e-3) –	6.5742e-1 (6.09e-2) –
WFG5	5	7.4375e-1 (4.53e-4)	5.9898e-1 (9.69e-4) –	7.4385e-1 (3.78e-4) =	7.1661e-1 (1.18e-2) –
	10	9.0472e-1 (2.50e-4)	7.6876e-1 (7.00e-4) –	9.0333e-1 (3.03e-4) –	8.2511e-1 (1.49e-2) –
	15	9.1756e-1 (2.50e-4)	8.2982e-1 (1.15e-3) –	9.1591e-1 (2.52e-4) –	3.0980e-1 (1.03e-1) –
WFG6	5	7.2159e-1 (1.32e-2)	5.8627e-1 (1.86e-2) –	7.2535e-1 (1.44e-2) =	7.2502e-1 (2.91e-2) =
	10	8.8790e-1 (1.79e-2)	7.4225e-1 (2.01e-2) –	8.7718e-1 (1.67e-2) –	8.6054e-1 (5.34e-2) –
	15	8.9955e-1 (2.46e-2)	7.9363e-1 (2.38e-2) –	7.2363e-1 (8.04e-2) –	6.2650e-1 (5.72e-2) –
WFG7	5	7.9404e-1 (5.38e-4)	6.4353e-1 (1.20e-3) –	7.8991e-1 (5.70e-4) –	7.8952e-1 (8.36e-3) –
	10	9.6965e-1 (2.60e-4)	8.2831e-1 (4.30e-3) –	9.5835e-1 (1.80e-3) –	9.6818e-1 (3.92e-3) =
	15	9.9072e-1 (9.04e-4)	8.9903e-1 (1.10e-3) –	9.8234e-1 (5.24e-3) –	7.5033e-1 (8.01e-2) –
WFG8	5	6.8107e-1 (1.14e-3)	4.6230e-1 (5.93e-3) –	6.7438e-1 (2.36e-3) –	3.1772e-1 (6.41e-3) –
	10	8.7577e-1 (6.90e-3)	6.0416e-1 (6.06e-2) –	8.3098e-1 (8.86e-2) =	6.4422e-1 (1.85e-2) –
	15	8.9925e-1 (1.56e-3)	7.6855e-1 (6.04e-2) –	7.7368e-1 (1.23e-1) –	5.1932e-1 (7.33e-2) –
WFG9	5	7.4084e-1 (4.55e-2)	6.3546e-1 (3.05e-3) –	7.5200e-1 (5.64e-3) =	5.5025e-1 (5.88e-2) –
	10	9.0376e-1 (4.59e-2)	8.1230e-1 (7.64e-3) –	8.8746e-1 (3.28e-2) –	8.0514e-1 (1.40e-2) –
	15	9.1408e-1 (3.94e-2)	8.4483e-1 (3.67e-2) –	8.3486e-1 (5.14e-2) –	2.6009e-1 (3.09e-2) –
	$ + \;/\; - \;/\; = $		7/19/1	2/20/5	2/18/7

下载: 导出CSV

表 4 各算法在DTLZ测试集上独立运行30次的HV均值和标准差

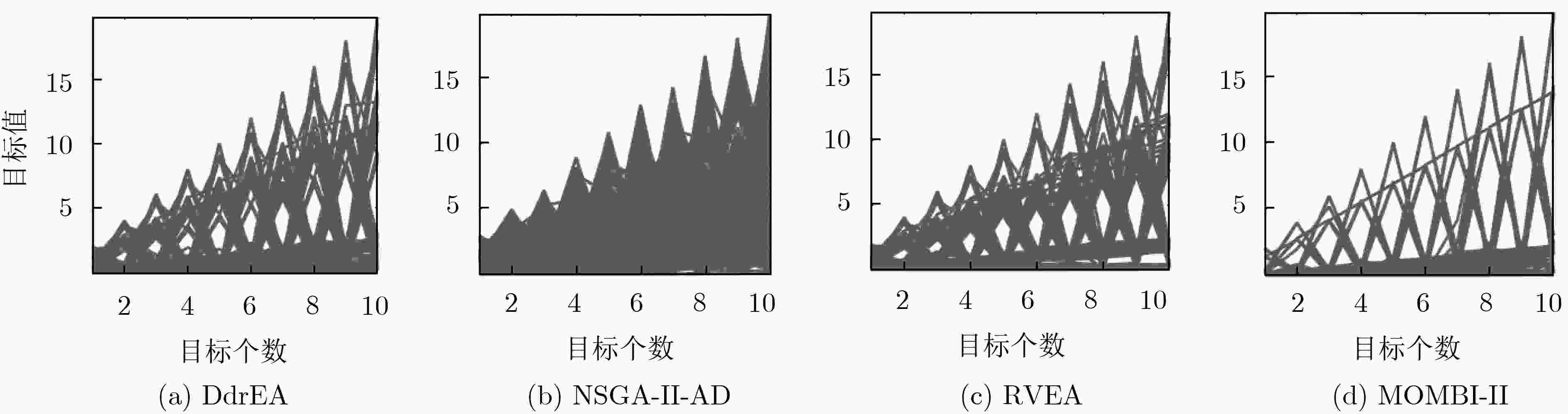
测试问题	M	DdrEA	NSGA-II/AD	RVEA	MOMBI-II
DTLZ1	5	8.4928e-1 (4.56e-2)	9.0703e-1 (4.42e-3) +	9.7490e-1 (1.72e-4) +	9.7461e-1 (2.59e-4) +
	10	9.8958e-1 (5.26e-3)	9.8084e-1 (1.48e-3) –	9.9968e-1 (1.73e-5) +	9.6198e-1 (3.15e-2) –
	15	9.1625e-1 (6.21e-2)	9.9583e-1 (3.87e-4) +	9.9990e-1 (4.62e-5) +	9.0337e-1 (3.90e-2) –
DTLZ2	5	7.9489e-1 (2.85e-4)	7.1691e-1 (5.66e-3) –	7.9479e-1 (3.56e-4) =	7.9449e-1 (5.39e-4) –
	10	9.7092e-1 (2.45e-4)	9.0347e-1 (4.42e-3) –	9.6974e-1 (1.49e-4) –	9.7085e-1 (2.13e-4) =
	15	9.9160e-1 (1.05e-4)	9.5411e-1 (3.00e-3) –	9.9109e-1 (2.99e-4) –	8.8008e-1 (6.31e-2) –
DTLZ3	5	6.2295e-1 (4.78e-2)	7.1455e-1 (7.51e-3) =	7.9246e-1 (2.06e-3) +	7.9042e-1 (2.58e-3) +
	10	8.8458e-1 (2.77e-2)	8.9986e-1 (5.59e-3) =	9.6952e-1 (3.56e-4) +	8.2910e-1 (9.36e-2) –
	15	7.0985e-1 (5.92e-2)	9.4928e-1 (5.01e-3) +	9.9072e-1 (2.96e-4) +	5.5538e-1 (5.08e-2) –
DTLZ4	5	7.9479e-1 (4.40e-4)	7.2830e-1 (5.61e-3) –	7.8505e-1 (2.91e-2) =	7.8426e-1 (2.85e-2) –
	10	9.7157e-1 (2.23e-4)	9.1475e-1 (4.07e-3) –	9.6980e-1 (1.53e-4) –	9.7226e-1 (2.24e-3) +
	15	9.9206e-1 (1.14e-4)	9.6070e-1 (2.35e-3) –	9.9076e-1 (1.18e-3) –	9.9044e-1 (1.51e-3) –
DTLZ5	5	1.0799e-1 (3.39e-3)	1.2935e-1 (3.74e-4) +	1.0483e-1 (2.04e-3) –	9.0959e-2 (2.73e-4) –
	10	9.1644e-2 (1.16e-3)	1.0062e-1 (2.77e-4) +	9.0893e-2 (1.10e-4) –	9.1359e-2 (7.19e-4) =
	15	9.1168e-2 (3.89e-4)	9.4858e-2 (3.18e-4) +	9.0648e-2 (3.24e-3) =	9.1206e-2 (3.78e-4) =
DTLZ6	5	1.0371e-1 (5.39e-3)	1.2924e-1 (2.68e-4) +	1.0340e-1 (1.29e-2) =	9.0959e-2 (2.53e-4) –
	10	9.1619e-2 (8.82e-4)	1.0053e-1 (2.70e-4) +	9.1873e-2 (8.07e-4) =	9.2808e-2 (1.11e-3) +
	15	9.1147e-2 (5.02e-4)	9.4877e-2 (2.90e-4) +	8.7721e-2 (1.72e-2) =	9.1664e-2 (5.93e-4) +
DTLZ7	5	2.4710e-1 (5.77e-3)	2.3300e-1 (4.51e-3) –	2.0265e-1 (3.05e-3) –	2.4292e-1 (5.42e-3) –
	10	1.9578e-1 (2.23e-3)	1.9180e-1 (3.40e-3) –	1.4878e-1 (2.05e-2) –	1.5877e-1 (1.00e-2) –
	15	1.6487e-1 (4.21e-3)	1.5882e-1 (5.21e-3) –	5.8918e-2 (5.77e-2) –	1.2108e-1 (1.74e-3) –
	$ + \;/\; - \;/\; = $		9/10/2	6/9/6	5/13/3

下载: 导出CSV

参考文献(15)

ZHOU Aimin, QU Boyang, LI Hui, et al. Multiobjective evolutionary algorithms: A survey of the state of the art[J]. Swarm and Evolutionary Computation, 2011, 1(1): 32–49. doi: 10.1016/j.swevo.2011.03.001

赖文星, 邓忠民, 张鑫杰. 基于多目标优化NSGA2改进算法的结构动力学模型确认[J]. 计算力学学报, 2018, 35(6): 669–674. doi: 10.7511/jslx20170828004

LAI Wenxing, DENG Zhongmin, and ZHANG Xinjie. Structural dynamics model validation based on NSGA2 improved algorithm[J]. Chinese Journal of Computational Mechanics, 2018, 35(6): 669–674. doi: 10.7511/jslx20170828004

LI Bingdong, LI Jinlong, TANG Ke, et al. Many-objective evolutionary algorithms: A survey[J]. ACM Computing Surveys, 2015, 48(1): 1–35. doi: 10.1145/2792984

HE Zhenan, YEN G G, and ZHANG Jun. Fuzzy-based Pareto optimality for many-objective evolutionary algorithms[J]. IEEE Transactions on Evolutionary Computation, 2014, 18(2): 269–285. doi: 10.1109/TEVC.2013.2258025

YANG Shengxiang, LI Miqing, LIU Xiaohui, et al. A grid-based evolutionary algorithm for many-objective optimization[J]. IEEE Transactions on Evolutionary Computation, 2013, 17(5): 721–736. doi: 10.1109/TEVC.2012.2227145

ZHANG Qingfu and LI Hui. MOEA/D: A multiobjective evolutionary algorithm based on decomposition[J]. IEEE Transactions on Evolutionary Computation, 2007, 11(6): 712–731. doi: 10.1109/TEVC.2007.892759

郑金华, 喻果, 贾月. 基于权重迭代的偏好多目标分解算法解决参考点对算法影响的研究[J]. 电子学报, 2016, 44(1): 67–76. doi: 10.3969/j.issn.0372-2112.2016.01.011

ZHENG Jinhua, YU Guo, and JIA Yue. Research on MOEA/D based on user-preference and alternate weight to solve the effect of reference point on multi-objective algorithms[J]. Acta Electronica Sinica, 2016, 44(1): 67–76. doi: 10.3969/j.issn.0372-2112.2016.01.011

BADER J and ZITZLER E. HypE: An algorithm for fast hypervolume-based many-objective optimization[J]. Evolutionary Computation, 2011, 19(1): 45–76. doi: 10.1162/EVCO_a_00009

CHENG Ran, JIN Yaochu, OLHOFER M, et al. A reference vector guided evolutionary algorithm for many-objective optimization[J]. IEEE Transactions on Evolutionary Computation, 2016, 20(5): 773–791. doi: 10.1109/TEVC.2016.2519378

LIU Yuan, ZHU Ningbo, LI Kenli, et al. An angle dominance criterion for evolutionary many-objective optimization[J]. Information Sciences, 2020, 509: 376–399. doi: 10.1016/J.INS.2018.12.078

HUBAND S, HINGSTON P, BARONE L, et al. A review of multiobjective test problems and a scalable test problem toolkit[J]. IEEE Transactions on Evolutionary Computation, 2006, 10(5): 477–506. doi: 10.1109/TEVC.2005.861417

DEB K, THIELE L, LAUMANNS M, et al. Scalable Test Problems for Evolutionary Multiobjective Optimization[M]. ABRAHAM A, JAIN L, and GOLDBERG R. Evolutionary Multiobjective Optimization. London: Springer, 2005: 105–145. doi: 10.1007/1-84628-137-7_6.

HERNÁNDEZ GÓMEZ R and COELLO COELLO C A. Improved metaheuristic based on the r2 indicator for many-objective optimization[C]. 2015 Annual Conference on Genetic and Evolutionary Computation. New York, USA: ACM, 2015: 679–686. doi: 10.1145/2739480.2754776.

DEB K. Multi-objective Optimisation Using Evolutionary Algorithms: An Introduction[M]. WANG L H, NG A H C, and DEB K. Multi-Objective Evolutionary Optimisation for Product Design and Manufacturing. London: Springer, 2011: 3–34. doi: 10.1007/978-0-85729-652-8_1.

DEB K and GOYAL M. A combined genetic adaptive search (GeneAS) for engineering design[J]. Journal of Computer Science and Informatics, 1996, 26: 30–45.

施引文献

资源附件(0)

访问统计