倒数粗糙熵图像阈值化分割算法

范九伦; 雷博

doi:10.11999/JEIT190559

倒数粗糙熵图像阈值化分割算法

doi: 10.11999/JEIT190559

范九伦,
雷博^,

1.
西安邮电大学通信与信息工程学院西安 710121
2.
电子信息现场勘验应用技术公安部重点实验室西安 710121

基金项目: 国家自然科学基金(61671377, 61571361, 61601362)，西安邮电大学西邮新星团队项目(xyt2016-01)

详细信息

作者简介:
范九伦：男，1964年生，教授，研究方向为模糊集理论、模糊信息处理、模式识别与图像处理、信息安全

雷博：女，1981年生，副教授，研究方向为模糊信息处理、粗糙集理论、图像分割

通讯作者:
雷博　leileibo@xupt.edu.cn

中图分类号: TP391.4
计量
- 文章访问数: 2326
- HTML全文浏览量: 837
- PDF下载量: 97
- 被引次数: 0
出版历程
- 收稿日期: 2019-07-25
- 修回日期: 2019-10-25
- 网络出版日期: 2019-11-13
- 刊出日期: 2020-01-21

Image Thresholding Segmentation Method Based on Reciprocal Rough Entropy

Jiulun FAN,
Bo LEI^,

1.
School of Communication and Information Engineering, Xi’an University of Posts & Telecommunications, Xi’an 710121, China
2.
Key Laboratory of Electronic Information Application Technology for Scene Investigation, Public Security Ministry, Xi’an 710121, China

Funds: The National Natural Science Foundation of China(61671377, 61571361, 61601362), The Project of New Star Team of Xi’an University of Posts & Telecommunications (xyt2016-01)

摘要

摘要:
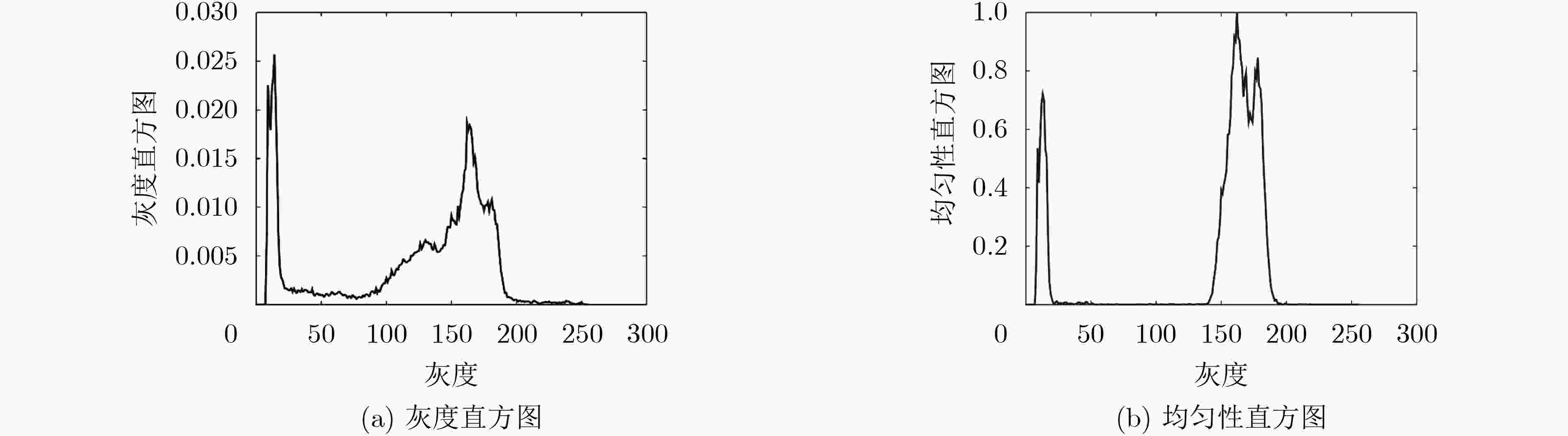
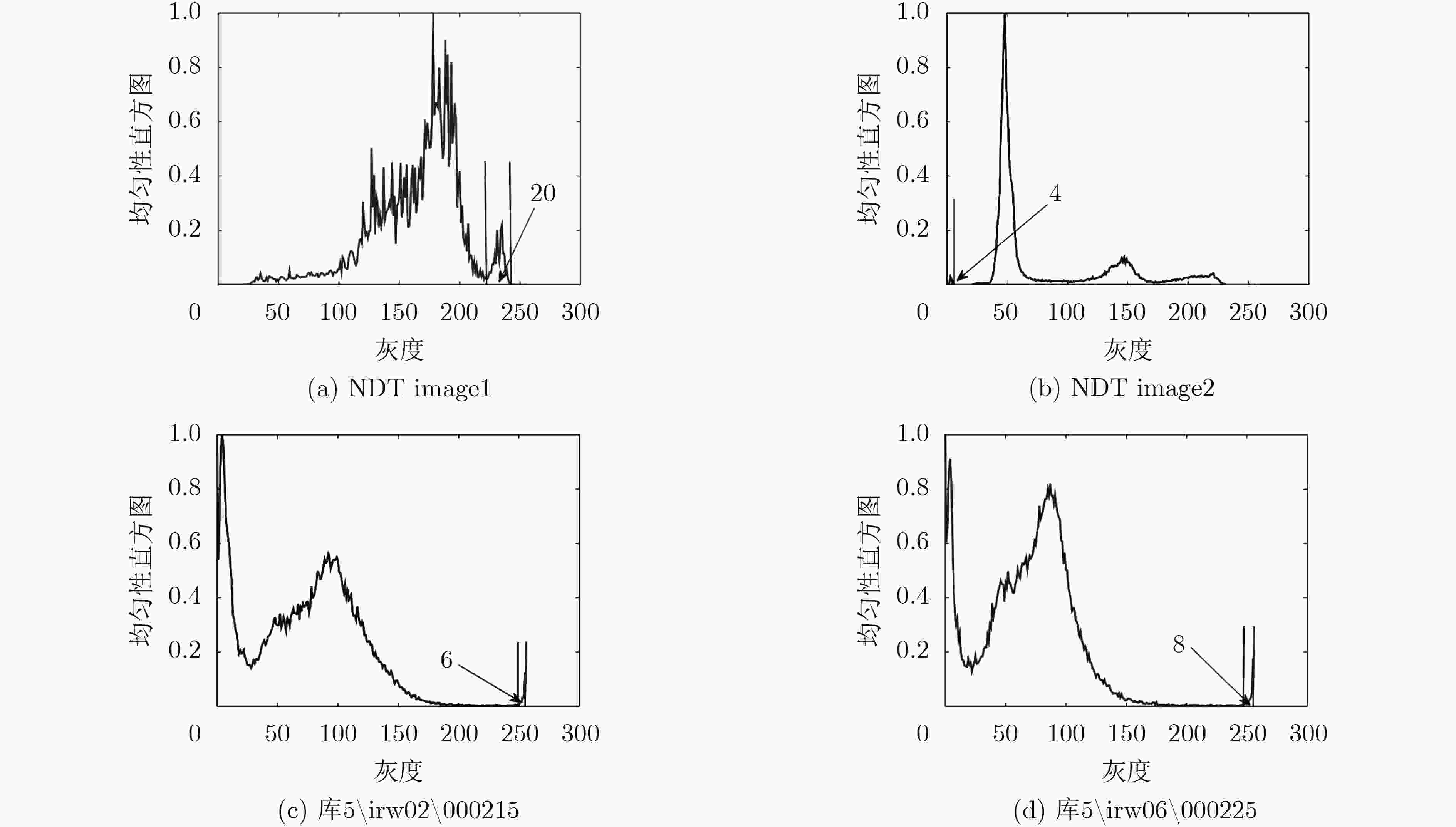
基于粗糙集理论的粗糙熵阈值法不需要图像之外的先验信息。粗糙熵阈值法需要解决两个问题，一是图像信息不完整性的度量，二是图像的粒化。该文基于倒数信息熵，提出一种倒数粗糙熵用来度量图像中信息的不完整性。为了更好地对图像进行粒化，采用一种基于均匀性直方图的粒子选取方式。该文提出的倒数粗糙熵表述简洁，计算简单。实验验证了该文方法的有效性。
- 图像处理 /
- 阈值分割 /
- 粗糙熵 /
- 倒数粗糙熵 /
- 粒化
Abstract:
Image thresholding methods based on the rough entropy segment the images without prior information except the images. There are two problems to be considered in the rough entropy based thresholding methods, i.e., measuring the incompleteness of knowledge about an image and granulating the image. In this paper, reciprocal rough entropy, a new form of rough entropy, is defined to measure the incompleteness of the image information. In order to granulate the image effectively, a granule size selection method based on the homogeneity histogram is employed. The proposed reciprocal rough entropy is simple in expression and calculation. The experimental results verify the effectiveness of the proposed algorithm.
- Image processing /
- Thresholding segmentation /
- Rough entropy /
- Reciprocal rough entropy /
- Granulation

HTML全文

图 1 cameraman 图像的直方图和均匀性直方图

下载: 全尺寸图片幻灯片

图 2 均匀性直方图及最小峰宽度

下载: 全尺寸图片幻灯片

图 3 NDT image1分割结果

下载: 全尺寸图片幻灯片

图 4 NDT image2分割结果

下载: 全尺寸图片幻灯片

图 5 OTCBVS\库5\irw02\000215分割结果

下载: 全尺寸图片幻灯片

图 6 OTCBVS\库5\irw06\000225分割结果

下载: 全尺寸图片幻灯片

表 1 6种算法的阈值比较

	最大粗糙熵法	模糊熵法	罗的方法	Masi熵法	倒数熵法	倒数粗糙熵法
NDT image1	177	51	(151,151)	83	116	221
NDT image2	52	177	(106,115)	45	160	72
D5\irw02\000215	68	75	(66,70)	46	148	211
D5\irw06\000225	65	75	(66,67)	46	128	209

下载: 导出CSV

表 2 6种算法的ME值与SSIM值比较

	NDT image1		NDT image2		D5\irw02\000215		D5\irw06\000225
	ME	SSIM	ME	SSIM	ME	SSIM	ME	SSIM
最大粗糙熵法	0.3605	0.0283	0.1996	0.5880	0.5556	0.0011	0.5671	0.0021
模糊熵法	0.9507	0.0015	0.2250	0.2345	0.5082	0.0013	0.4722	0.0029
罗的方法	0.6341	0.0098	0.0077	0.9822	0.5596	0.0013	0.5679	0.0021
Masi熵法	0.9136	0.0033	0.5470	0.1658	0.6841	0.0007	0.7181	0.0013
倒数熵法	0.8486	0.0049	0.2041	0.3172	0.0366	0.1367	0.0461	0.1585
倒数粗糙熵法	0.0016	0.9765	0.0429	0.9015	0.0051	0.7286	0.0084	0.6833

下载: 导出CSV

参考文献(28)

SEZGIN M and SANKUR B. Survey over image thresholding techniques and quantitative performance evaluation[J]. Journal of Electronic Imaging, 2004, 13(1): 146–165. doi: 10.1117/1.1631315

OLIVA D, HINOJOSA S, CUEVAS E, et al. Cross entropy based thresholding for magnetic resonance brain images using Crow Search Algorithm[J]. Expert Systems with Applications, 2017, 79: 164–180. doi: 10.1016/j.eswa.2017.02.042

聂方彦, 李建奇, 张平凤, 等. 复杂图像的Kaniadakis熵阈值分割方法[J]. 激光与红外, 2017, 47(8): 1040–1045. doi: 10.3969/j.issn.1001-5078.2017.08.022

NIE Fangyan, LI Jianqi, ZHANG Pingfeng, et al. Threshold segmentation method of complex image based on Kaniadakis entropy[J]. Laser &Infrared, 2017, 47(8): 1040–1045. doi: 10.3969/j.issn.1001-5078.2017.08.022

NG H F. Automatic thresholding for defect detection[J]. Pattern Recognition Letters, 2006, 27(14): 1644–1649. doi: 10.1016/j.patrec.2006.03.009

BHANDARI A K, KUMAR A, and SINGH G K. Tsallis entropy based multilevel thresholding for colored satellite image segmentation using evolutionary algorithms[J]. Expert Systems with Applications, 2015, 42(22): 8707–8730. doi: 10.1016/j.eswa.2015.07.025

PAL S K, SHANKAR B U, and MITRA P. Granular computing, rough entropy and object extraction[J]. Pattern Recognition Letters, 2005, 26(16): 2509–2517. doi: 10.1016/j.patrec.2005.05.007

PAWLAK Z. Rough sets[J]. International Journal of Computer & Information Sciences, 1982, 11(5): 341–356. doi: 10.1007/BF01001956

PAWLAK Z. Rough Sets: Theoretical Aspects of Reasoning about Data[M]. Dordrecht: Springer, 1991: 2−8.

岳晓冬, 苗夺谦, 钟才明. 基于粗糙性度量的彩色图像分割方法[J]. 自动化学报, 2010, 36(6): 807–816.

YUE Xiaodong, MIAO Duoqian, and ZHONG Caiming. Roughness measure approach to color image segmentation[J]. Acta Automatica Sinica, 2010, 36(6): 807–816.

吴涛. 图像阈值化的自适应粗糙熵方法[J]. 中国图象图形学报, 2014, 19(1): 1–10. doi: 10.11834/jig.20140101

WU Tao. Adaptive rough entropy method for image thresholding[J]. Journal of Image and Graphics, 2014, 19(1): 1–10. doi: 10.11834/jig.20140101

姚龙洋, 张清华, 胡帅鹏, 等. 基于近似集与粒子群的粗糙熵图像分割方法[J]. 计算机科学与探索, 2016, 10(5): 699–708.

YAO Longyang, ZHANG Qinghua, HU Shuaipeng, et al. Rough entropy for image segmentation based on approximation sets and particle swarm optimization[J]. Journal of Frontiers of Computer Science and Technology, 2016, 10(5): 699–708.

刘丽华, 周涛, 周乾智. 基于VPRS粗糙熵的图像分割[J]. 计算机工程与应用, 2018, 54(20): 178–183. doi: 10.3778/j.issn.1002-8331.1804-0090

LIU Lihua, ZHOU Tao, and ZHOU Qianzhi. Image segmentation on entropy of variable precision rough entropy[J]. Computer Engineering and Applications, 2018, 54(20): 178–183. doi: 10.3778/j.issn.1002-8331.1804-0090

SARDAR M, MITRA S, and SHANKAR B U. Iris localization using rough entropy and CSA: A soft computing approach[J]. Applied Soft Computing, 2018, 67: 61–69. doi: 10.1016/j.asoc.2018.02.047

HASSANIEN A E, ABRAHAM A, PETERS J F, et al. Rough sets and near sets in medical imaging: A review[J]. IEEE Transactions on Information Technology in Biomedicine, 2009, 13(6): 955–968. doi: 10.1109/TITB.2009.2017017

SEN D and PAL S K. Generalized rough sets, entropy, and image ambiguity measures[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics) , 2009, 39(1): 117–128. doi: 10.1109/TSMCB.2008.2005527

SEN D and PAL S K. Histogram thresholding using beam theory and ambiguity measures[J]. Fundamenta Informaticae, 2007, 75(1/4): 483–504.

MAŁYSZKO D and STEPANIUK J. Adaptive multilevel rough entropy evolutionary thresholding[J]. Information Sciences, 2010, 180(7): 1138–1158. doi: 10.1016/j.ins.2009.11.034

邓廷权, 盛春冬. 结合变精度粗糙熵和遗传算法的图像阈值分割方法[J]. 控制与决策, 2011, 26(7): 1079–1082.

DENG Tingquan and SHENG Chundong. Image threshold segmentation based on entropy of variable precision rough sets and genetic algorithm[J]. Control and Decision, 2011, 26(7): 1079–1082.

吴尚智, 佘志用, 张霞, 等. 利用变精度粗糙熵的图像分割算法[J]. 计算机工程与科学, 2018, 40(10): 1837–1843. doi: 10.3969/j.issn.1007-130X.2018.10.016

WU Shangzhi, SHE Zhiyong, HANG Xia, et al. An image segmentation algorithm using variable precision rough entropy[J]. Computer Engineering &Science, 2018, 40(10): 1837–1843. doi: 10.3969/j.issn.1007-130X.2018.10.016

PAL N R and PAL S K. Entropic thresholding[J]. Signal Processing, 1989, 16(2): 97–108. doi: 10.1016/0165-1684(89)90090-X

吴一全, 占必超. 基于混沌粒子群优化的倒数熵阈值选取方法[J]. 信号处理, 2010, 26(7): 1044–1049. doi: 10.3969/j.issn.1003-0530.2010.07.015

WU Yiquan and ZHAN Bichao. Thresholding based on reciprocal entropy and chaotic particle swarm optimization[J]. Signal Processing, 2010, 26(7): 1044–1049. doi: 10.3969/j.issn.1003-0530.2010.07.015

吴一全, 殷骏, 毕硕本. 最大倒数熵/倒数灰度熵多阈值选取[J]. 信号处理, 2013, 29(2): 143–151. doi: 10.3969/j.issn.1003-0530.2013.02.001

WU Yiquan, YIN Jun, and BI Shuoben. Multi-threshold selection using maximum reciprocal entropy/reciprocal gray entropy[J]. Journal of Signal Processing, 2013, 29(2): 143–151. doi: 10.3969/j.issn.1003-0530.2013.02.001

CHENG Hengda and SUN Ying. A hierarchical approach to color image segmentation using homogeneity[J]. IEEE Transactions on Image Processing, 2000, 9(12): 2071–2082. doi: 10.1109/83.887975

罗钧, 杨永松, 侍宝玉. 基于改进的自适应差分演化算法的二维Otsu多阈值图像分割[J]. 电子与信息学报, 2019, 41(8): 2017–2024. doi: 10.11999/JEIT180949

LUO Jun, YANG Yongsong, and SHI Baoyu. Multi-threshold image segmentation of 2D Otsu based on improved adaptive differential evolution algorithm[J]. Journal of Electronics &Information Technology, 2019, 41(8): 2017–2024. doi: 10.11999/JEIT180949

SHUBHAM S and BHANDARI A K. A generalized Masi entropy based efficient multilevel thresholding method for color image segmentation[J]. Multimedia Tools and Applications, 2019, 78(12): 17197–17238. doi: 10.1007/s11042-018-7034-x

LI Xueqin, ZHAO Zhiwei, and CHENG H S. Fuzzy entropy threshold approach to breast cancer detection[J]. Information Sciences - Applications, 1995, 4(1): 49–56. doi: 10.1016/1069-0115(94)00019-x

http://vcipl-okstate.org/pbvs/bench/, 2013.

WANG Zhou, BOVIK A C, SHEIKH H R, et al. Image quality assessment: From error visibility to structural similarity[J]. IEEE Transactions on Image Processing, 2004, 13(4): 600–612. doi: 10.1109/TIP.2003.819861

施引文献

资源附件(0)

访问统计