Research on the Dynamic Sparse Bayesian Recovery of Multi-task Observed Streaming Signals in Time Domain
-
摘要:
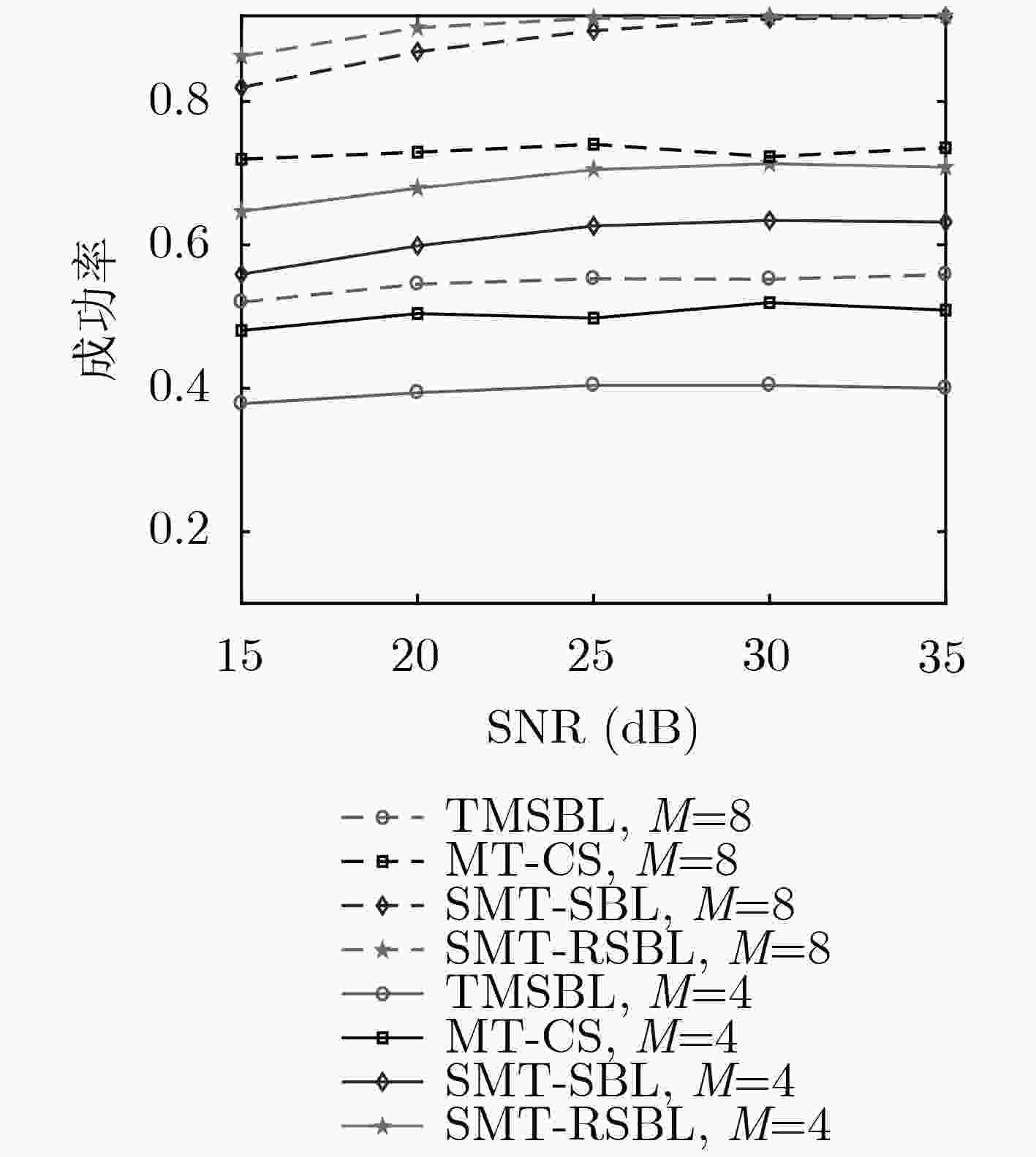
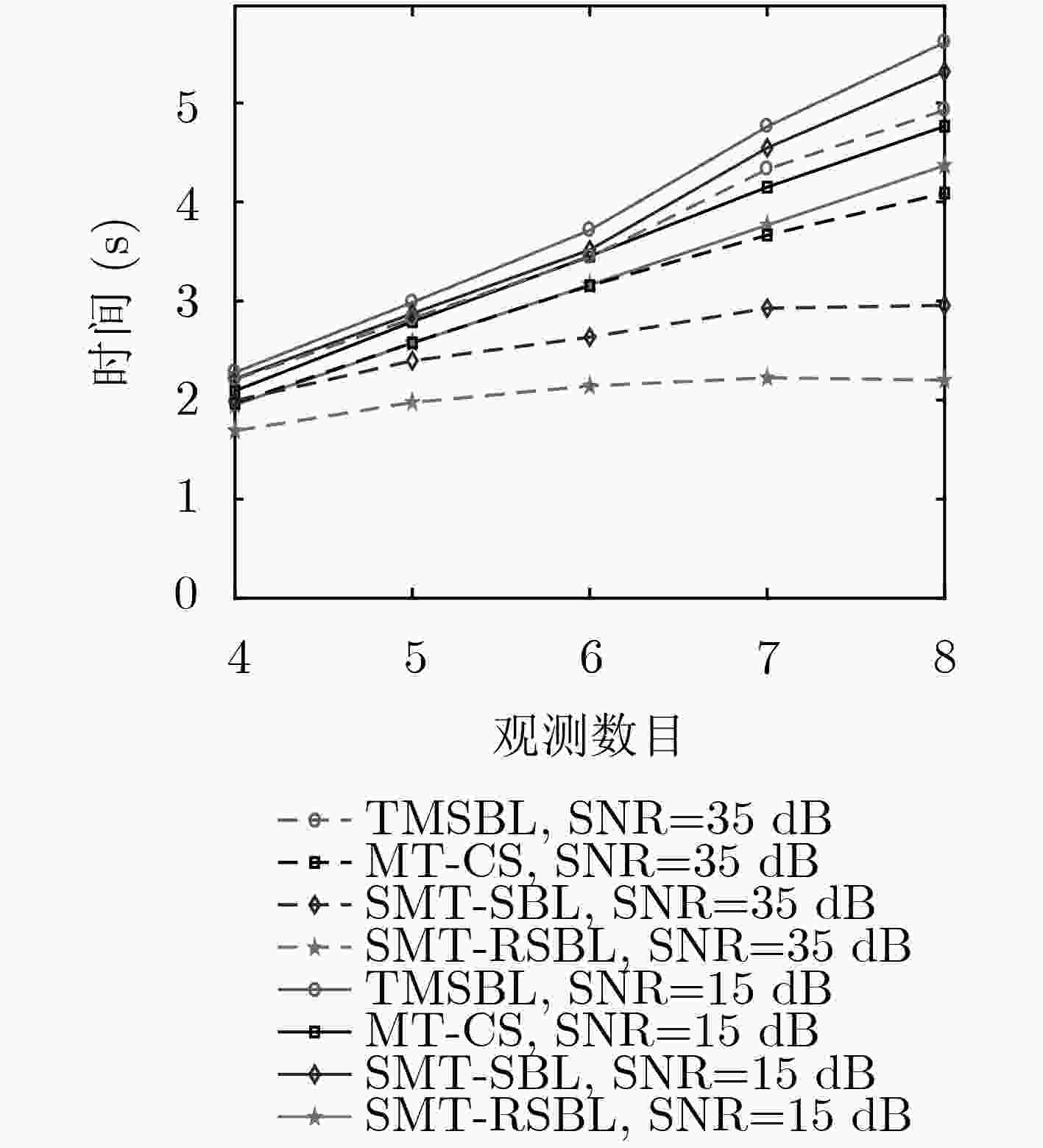
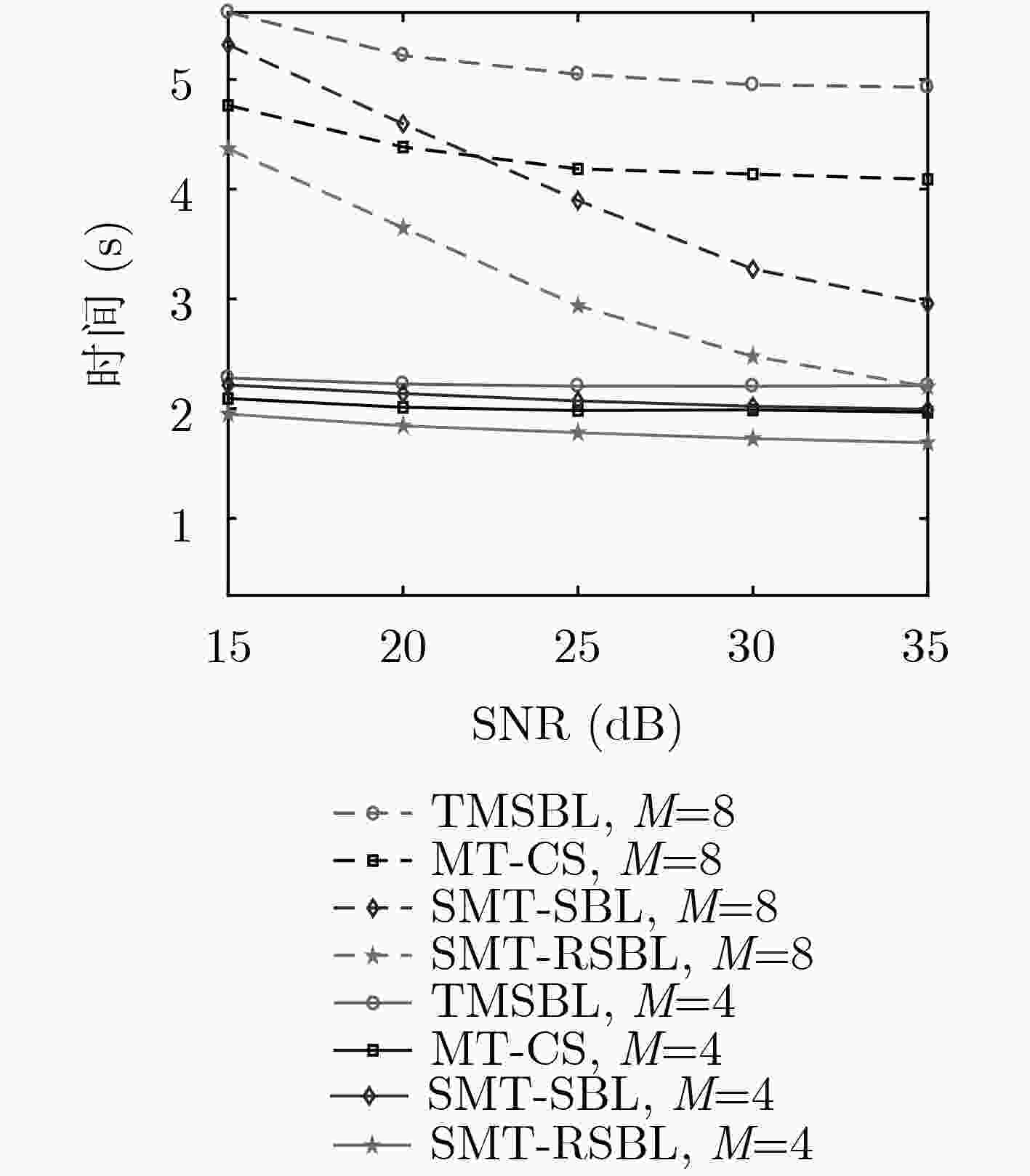
为了解决多任务观测条件下时域流信号动态重构面临的块效应问题,该文基于重叠正交变换(LOT)和稀疏贝叶斯学习的贪婪重构框架先后提出了一种流信号多任务稀疏贝叶斯学习算法及其鲁棒增强型的改进算法,前者将LOT时域滑窗推广到多任务条件下,通过贝叶斯概率建模将未知的噪声精度的估计任务从信号重构中解耦并省略,后者进一步引入了重构不确定性的度量,提高了算法的鲁棒性和抑制误差积累的能力。基于浮标实测数据的实验结果表明,相比多任务重构领域代表性较强的时间多稀疏贝叶斯学习(TMSBL)和多任务压缩感知(MT-CS)算法,本文算法在不同信噪比、观测数目和任务数目条件下具有显著更高的重构精度、成功率和效率。
Abstract:To eliminate the blocking effects in the dynamic recovery of the streaming signals observed from multiple tasks in time domain, a streaming multi-task sparse Bayesian learning based algorithm and its robust enhanced version are proposed in this paper, where the former extends Lapped Orthogonal Transform (LOT) sliding window in time domain to multi-task condition, and decouples the estimation of unknown noise accuracy from signal reconstruction by Bayesian probability modeling and omits it, the latter further introduces the measurement of reconstructed uncertainty, which improves the robustness of the algorithm and the ability to suppress the accumulation of errors. Experimental results based on measured meteorological data shows that the proposed algorithms have significantly higher reconstruction accuracy, success rate and running speed than the representative algorithms in the field of compressed sensing from multiple measurement vectors, namely, the Temporal Multiple Sparse Bayesian Learning (TMSBL) algorithm and the Multi-Task-Compressed Sensing (MT-CS) algorithm, under different conditions of Signal-to-Noise Ratios, number of observations and tasks.
-
Key words:
- Signal processing /
- Streaming signals /
- Multi-task /
- Sparse Bayesian /
- Blocking effects
-
表 1 目标函数、中间变量及超参数估计公式列表
目标函数及其分解形式(其中${\tilde a_l} = 2{a_l} + M\left( {2d + 2} \right)$): $L\left( { { { {\bar{ \alpha } } }_t} } \right) = { { - \displaystyle\sum\limits_{l = 1}^L {\left\{ { { {\tilde a}_l}\ln \left( { {\bar{ y} }_{t,l}^{\rm{T} }{\bar{ C} }_l^{ - 1}{ { {\bar{ y} } }_{t,l} } + 2{b_l} } \right) + \ln \left| { { { {\bar{ C} } }_l} } \right|} \right\} } } / 2} \;\;\quad (29)$ $L\left( { { { {\bar{ \alpha } } }_t} } \right) = { { - \displaystyle\sum\limits_{l = 1}^L {\left\{ { { {\tilde a}_l}\ln \left( {1 - \frac{ { { {q_{j,l}^2} / { {g_{j,l} } } } } }{ { {\alpha _j} + {s_{j,l} } } }} \right) + \ln \left( {1 - \alpha _j^{ - 1}{s_{j,l} } } \right)} \right\} } } / 2}\;\; (30)$ 中间变量: ${{\bar{ C}}_l} = {{I}} + {{{\varPsi }}_l}{\bar{ A}}_t^{ - 1}{{\varPsi }}_l^{\rm{T}},_{}^{}{{\bar{ C}}_{ - j,l}} = {{I}} + \displaystyle\sum\limits_{k \ne j} {\alpha _k^{ - 1}{{{\psi }}_{k,l}}{{\psi }}_{k,l}^{\rm{T}}} \left( {{\rm{SMT - SBL}}} \right)\;\; (31)$ ${{\bar{ C}}_l} = {{\hat{ \varOmega }}_{t,l}} + {{{\varPsi }}_l}{\bar{ A}}_t^{ - 1}{{\varPsi }}_l^{\rm{T}},{{\bar{ C}}_{ - j,l}} = {{\hat{ \varOmega }}_{t,l}} + \displaystyle\sum\limits_{k \ne j} {\alpha _k^{ - 1}{{{\psi }}_{k,l}}{{\psi }}_{k,l}^{\rm{T}}} \left( {{\rm{SMT - RSBL}}} \right)\;\;\;(32)$ ${s_{j,l}} = {{\psi }}_{j,l}^{\rm{T}}{\bar{ C}}_{ - j,l}^{ - 1}{{{\psi }}_{j,l}},_{}^{}{q_{j,l}} = {{\psi }}_{j,l}^{\rm{T}}{\bar{ C}}_{ - j,l}^{ - 1}{{\bar{ y}}_{t,l}},_{}^{}{g_{j,l}} = {\bar{ y}}_{t,l}^{\rm{T}}{\bar{ C}}_{ - j,l}^{ - 1}{{\bar{ y}}_{t,l}} + 2{b_l}\;\;\; (33)$ ${S_{j,l}} = {{\psi }}_{j,l}^{\rm{T}}{\bar{ C}}_l^{ - 1}{{{\psi }}_{j,l}},_{}^{}{Q_{j,l}} = {{\psi }}_{j,l}^{\rm{T}}{\bar{ C}}_l^{ - 1}{{\bar{ y}}_{t,l}},_{}^{}{G_l} = {\bar{ y}}_{t,l}^{\rm{T}}{\bar{ C}}_l^{ - 1}{{\bar{ y}}_{t,l}} + 2{b_l}\;\;\; (34)$ ${\alpha _j}$更新公式: ${\alpha _j} = \left\{ \begin{aligned} & {L / { {\theta _j} } },{\theta _j} > 0\\ & \infty ,\quad {\simfont\text{其他} } \end{aligned} \right.\;\;\;\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad (35)$ ${\theta _j} = \displaystyle\sum\limits_{l = 1}^L {\frac{ { { {\tilde a}_l}({ {q_{j,l}^2} / { {g_{j,l} } } }) - {s_{j,l} } } }{ { {s_{j,l} }({s_{j,l} } - { {q_{j,l}^2} / { {g_{j,l} } } })} } } \;\;\;\;\qquad\qquad\qquad\qquad\qquad\qquad\quad (36)$ 表 2 相关的快速更新公式列表
添加原子${{{\psi }}_{j,l}}$ 删除原子${{{\psi }}_{j,l}}$ 维持原子${{{\psi }}_{j,l}}$ 说明 $ {\rm{SMT - SBL}}:$ $ {\rm{SMT - SBL}}:$ $ {\rm{SMT - SBL}}:$ 添加情形中: $ \begin{array}{l} {{\tilde{\hat{ \varSigma }}}}_{t,l}^{{\bar{ w}}} = [{\hat{ \varSigma }}_{t,l}^{{\bar{ w}}} + {{\hat \varSigma }_{jj,l}}{\hat{ \varSigma }}_{t,l}^{{\bar{ w}}}{{\varPsi }}_l^{\rm{T}}{{{\psi }}_{j,l}}{{\psi }}_{j,l}^{\rm{T}}{{{\varPsi }}_l}{\hat{ \varSigma }}_{t,l}^{{\bar{ w}}},\\ - {{\hat \varSigma }_{jj,l}}{\hat{ \varSigma }}_{t,l}^{{\bar{ w}}}{{\varPsi }}_l^{\rm{T}}{{{\psi }}_{j,l}}; - {{\hat \varSigma }_{jj,l}}{{\psi }}_{j,l}^{\rm{T}}{{\varPsi }}_l^{}{\hat{ \varSigma }}_{t,l}^{{\bar{ w}}},{{\hat \varSigma }_{jj,l}}]\\ {\tilde{ \mu }}_{t,l}^{{\bar{ w}}} = [{{\mu }}_{t,l}^{{\bar{ w}}} + {\mu _{j,l}}{\hat{ \varSigma }}_{t,l}^{{\bar{ w}}}{{\varPsi }}_l^{\rm{T}}{{{\psi }}_{j,l}};{\mu _{j,l}}]\\ {{{e}}_{j,l}} = {{{\psi }}_{j,l}} - {{{\varPsi }}_l}{\hat{ \varSigma }}_{t,l}^{{\bar{ w}}}{{\varPsi }}_l^{\rm{T}}{{{\psi }}_{j,l}} \end{array}$ $ \begin{array}{l} {{\tilde S}_{k,l}} = {S_{k,l}} + {{{{({\hat{ \varSigma }}_{j,l}^{\rm{T}}{{\varPsi }}_l^{\rm{T}}{{{\psi }}_{k,l}})}^2}} / {{{\hat \varSigma }_{jj,l}}}}\\ {{\tilde Q}_{k,l}} = {Q_{k,l}} + {{{\mu _{j,l}}{\hat{ \varSigma }}_{j,l}^{\rm{T}}{{\varPsi }}_l^{\rm{T}}{{{\psi }}_{k,l}}} / {{{\hat \varSigma }_{jj,l}}}}\\ {{\tilde G}_l} = {G_l} + {{{{({\hat{ \varSigma }}_{j,l}^{\rm{T}}{{\varPsi }}_l^{\rm{T}}{{{\bar{ y}}}_{t,l}})}^2}} / {{{\hat \varSigma }_{jj,l}}}} \end{array}$ $ \begin{array}{l} {{\tilde S}_{k,l}} = {S_{k,l}} + {\gamma _{j,l}}{({\hat{ \varSigma }}_{j,l}^{\rm{T}}{{\varPsi }}_l^{\rm{T}}{{{\psi }}_{k,l}})^2}\\ {{\tilde Q}_{k,l}} = {Q_{k,l}} + {\gamma _{j,l}}{\mu _{j,l}}{\hat{ \varSigma }}_{j,l}^{\rm{T}}{{\varPsi }}_l^{\rm{T}}{{{\psi }}_{k,l}}\\ {{\tilde G}_l} = {G_l} + {\gamma _{j,l}}{({\hat{ \varSigma }}_{j,l}^{\rm{T}}{{\varPsi }}_l^{\rm{T}}{{{\bar{ y}}}_{t,l}})^2} \end{array}$ $ \begin{array}{l} {{\hat \varSigma }_{jj,l}} = {\left( {{{\tilde \alpha }_j} + {S_{j,l}}} \right)^{ - 1}},\\ {\mu _{j,l}} = {{\hat \varSigma }_{jj,l}}{Q_{j,l}} \end{array}$ $ {\rm{SMT - RSBL}}:$ $ {\rm{SMT - RSBL}}:$ $ {\rm{SMT - RSBL}}:$ 删除情形中: $ \begin{array}{l} {{\tilde{\hat{ \varSigma }}}}_{t,l}^{{\bar{ w}}} = [{\hat{ \varSigma }}_{t,l}^{{\bar{ w}}} + {{\hat \varSigma }_{jj,l}}{\hat{ \varSigma }}_{t,l}^{{\bar{ w}}}{{\varPsi }}_l^{\rm{T}}{\hat{ \varOmega }}_{t,l}^{ - 1}{{{\psi }}_{j,l}}{{\psi }}_{j,l}^{\rm{T}}{\hat{ \varOmega }}_{t,l}^{ - 1}{{{\varPsi }}_l}{\hat{ \varSigma }}_{t,l}^{{\bar{ w}}},\\ - {{\hat \varSigma }_{jj,l}}{\hat{ \varSigma }}_{t,l}^{{\bar{ w}}}{{\varPsi }}_l^{\rm{T}}{\hat{ \varOmega }}_{t,l}^{ - 1}{{{\psi }}_{j,l}}; - {{\hat \varSigma }_{jj,l}}{{\psi }}_{j,l}^{\rm{T}}{\hat{ \varOmega }}_{t,l}^{ - 1}{{\varPsi }}_l^{}{\hat{ \varSigma }}_{t,l}^{{\bar{ w}}},{{\hat \varSigma }_{jj,l}}]\\ {\tilde{ \mu }}_{t,l}^{{\bar{ w}}} = [{{\mu }}_{t,l}^{{\bar{ w}}} + {\mu _{j,l}}{\hat{ \varSigma }}_{t,l}^{{\bar{ w}}}{{\varPsi }}_l^{\rm{T}}{\hat{ \varOmega }}_{t,l}^{ - 1}{{{\psi }}_{j,l}};{\mu _{j,l}}]\\ {{{e}}_{j,l}} = ({\hat{ \varOmega }}_{t,l}^{ - 1} - {\hat{ \varOmega }}_{t,l}^{ - 1}{{{\varPsi }}_l}{\hat{ \varSigma }}_{t,l}^{{\bar{ w}}}{{\varPsi }}_l^{\rm{T}}{\hat{ \varOmega }}_{t,l}^{ - 1}){{{\psi }}_{j,l}} \end{array}$ $ \begin{array}{l} {{\tilde S}_{k,l}} = {S_{k,l}} + {{{{({\hat{ \varSigma }}_{j,l}^{\rm{T}}{{\varPsi }}_l^{\rm{T}}{\hat{ \varOmega }}_{t,l}^{ - 1}{{{\psi }}_{k,l}})}^2}} / {{{\hat \varSigma }_{jj,l}}}}\\ {{\tilde Q}_{k,l}} = {Q_{k,l}} + {{{\mu _{j,l}}{\hat{ \varSigma }}_{j,l}^{\rm{T}}{{\varPsi }}_l^{\rm{T}}{\hat{ \varOmega }}_{t,l}^{ - 1}{{{\psi }}_{k,l}}} / {{{\hat \varSigma }_{jj,l}}}}\\ {{\tilde G}_l} = {G_l} + {{{{({\hat{ \varSigma }}_{j,l}^{\rm{T}}{{\varPsi }}_l^{\rm{T}}{\hat{ \varOmega }}_{t,l}^{ - 1}{{{\bar{ y}}}_{t,l}})}^2}} / {{{\hat \varSigma }_{jj,l}}}} \end{array}$ $ \begin{array}{l} {{\tilde S}_{k,l}} = {S_{k,l}} + {\gamma _{j,l}}{({\hat{ \varSigma }}_{j,l}^{\rm{T}}{{\varPsi }}_l^{\rm{T}}{\hat{ \varOmega }}_{t,l}^{ - 1}{{{\psi }}_{k,l}})^2}\\ {{\tilde Q}_{k,l}} = {Q_{k,l}} + {\gamma _{j,l}}{\mu _{j,l}}{\hat{ \varSigma }}_{j,l}^{\rm{T}}{{\varPsi }}_l^{\rm{T}}{\hat{ \varOmega }}_{t,l}^{ - 1}{{{\psi }}_{k,l}}\\ {{\tilde G}_l} = {G_l} + {\gamma _{j,l}}{({\hat{ \varSigma }}_{j,l}^{\rm{T}}{{\varPsi }}_l^{\rm{T}}{\hat{ \varOmega }}_{t,l}^{ - 1}{{{\bar{ y}}}_{t,l}})^2} \end{array}$ ${\hat \varSigma _{jj,l}}$是${\hat{ \varSigma }}_{t,l}^{{\bar{ w}}}$的第$j$个对角元素,${{\hat{ \varSigma }}_{j,l}}$是${\hat{ \varSigma }}_{t,l}^{{\bar{ w}}}$的第$j$列,${\mu _{j,l}}$是${{\mu }}_{t,l}^{{\bar{ w}}}$的第$j$个元素。 通用公式: 通用公式: 通用公式: 维持情形中: $ \begin{array}{l} {{\tilde S}_{k,l}} = {S_{k,l}} - {{\hat \varSigma }_{jj,l}}{({{\psi }}_{k,l}^{\rm{T}}{{{e}}_{j,l}})^2}\\ {{\tilde Q}_{k,l}} = {Q_{k,l}} - {\mu _{j,l}}{{\psi }}_{k,l}^{\rm{T}}{{{e}}_{j,l}}\\ {{\tilde G}_l} = {G_l} - {{\hat \varSigma }_{jj,l}}{({\bar{ y}}_{t,l}^{\rm{T}}{{{e}}_{j,l}})^2}\\ 2\Delta L = \sum\nolimits_{l = 1}^L {\ln \left[ {{{{{\tilde \alpha }_j}} / {\left( {{{\tilde \alpha }_j} + {s_{j,l}}} \right)}}} \right]} \\ \mathop {}\nolimits - \sum\nolimits_{l = 1}^L {{{\tilde a}_l}\ln \left[ {1 - {{\left( {{{q_{j,l}^2} / {{g_{j,l}}}}} \right)} / {\left( {{{\tilde \alpha }_j} + {s_{j,l}}} \right)}}} \right]} \end{array}$ $ \begin{array}{l} 2\Delta L = - \sum\nolimits_{l = 1}^L {\ln \left( {1 - {{{S_{j,l}}} / {{\alpha _j}}}} \right)} \\ \mathop {}\nolimits \mathop {}\nolimits - \sum\nolimits_{l = 1}^L {{{\tilde a}_l}} \ln \left[ {1 + \frac{{{{Q_{j,l}^2} / {{G_l}}}}}{{{\alpha _j} - {S_{j,l}}}}} \right]\\ {{\tilde{\hat{ \varSigma }}}}_{t,l}^{{\bar{ w}}} = {\hat{ \varSigma }}_{t,l}^{{\bar{ w}}} - {{{{{\hat{ \varSigma }}}_{j,l}}{\hat{ \varSigma }}_{j,l}^{\rm{T}}} / {{{\hat \varSigma }_{jj,l}}}}\\ {\tilde{ \mu }}_{t,l}^{{\bar{ w}}} = {{\mu }}_{t,l}^{{\bar{ w}}} - {\mu _{j,l}}{{{{{\hat{ \varSigma }}}_{j,l}}} / {{{\hat \varSigma }_{jj,l}}}} \end{array}$ $ \begin{array}{l} 2\Delta L = \sum\nolimits_{l = 1}^L {\left( {{{\tilde a}_l} - 1} \right)\ln \left( {1 + \frac{{{\alpha _j} - {{\tilde \alpha }_j}}}{{{\alpha _j}{{\tilde \alpha }_j}}}} \right)} \\ + \sum\nolimits_{l = 1}^L {{{\tilde a}_l}} \ln \frac{{\left[ {\left( {{\alpha _j} + {s_{j,l}}} \right){g_{j,l}} - q_{j,l}^2} \right]{{\tilde \alpha }_j}}}{{\left[ {\left( {{{\tilde \alpha }_j} + {s_{j,l}}} \right){g_{j,l}} - q_{j,l}^2} \right]{\alpha _j}}}\\ {{\tilde{\hat{ \varSigma }}}}_{t,l}^{{\bar{ w}}} = {\hat{ \varSigma }}_{t,l}^{{\bar{ w}}} - {\gamma _{j,l}}{{{\hat{ \varSigma }}}_{j,l}}{\hat{ \varSigma }}_{j,l}^{\rm{T}}\\ {\tilde{ \mu }}_{t,l}^{{\bar{ w}}} = {{\mu }}_{t,l}^{{\bar{ w}}} - {\gamma _{j,l}}{\mu _{j,l}}{{{\hat{ \varSigma }}}_{j,l}} \end{array}$ ${\hat \varSigma _{jj,l}},{{\hat{ \varSigma }}_{j,l}},{\mu _{j,l}}$与前述相同,${\gamma _{j,l}} = {\left[ {{{\hat \varSigma }_{jj,l}} + {{\left( {{{\tilde \alpha }_j} - {\alpha _j}} \right)}^{ - 1}}} \right]^{ - 1}}$。 -
LEINONEN M, CODREANU M, and JUNTTI M. Sequential compressed sensing with progressive signal reconstruction in wireless sensor networks[J]. IEEE Transactions on Wireless Communications, 2015, 14(3): 1622–1635. doi: 10.1109/TWC.2014.2371017 ASIF M S and ROMBERG J. Sparse recovery of streaming signals using ℓ1-homotopy[J]. IEEE Transactions on Signal Processing, 2014, 62(16): 4209–4223. doi: 10.1109/TSP.2014.2328981 周超杰, 张杰, 杨俊钢, 等. 基于ROMS模式的南海SST与SSH四维变分同化研究[J]. 海洋学报, 2019, 41(1): 32–40. doi: 10.3969/j.issn.0253-4193.2019.01.005ZHOU Chaojie, ZHANG Jie, YANG Jungang, et al. 4DVAR assimilation of SST and SSH data in South China Sea based on ROMS[J]. Acta Oceanologica Sinica, 2019, 41(1): 32–40. doi: 10.3969/j.issn.0253-4193.2019.01.005 ZHANG Yonggang, ZHANG Jianxue, JIAO Lin, et al. Algorithms of wave reflective critical angle on interface[C]. SPIE 10250, International Conference on Optical and Photonics Engineering, Chengdu, China, 2017: 8–13. doi: 10.1117/12.2266713. AO Dongyang, WANG Rui, HU Cheng, et al. A sparse SAR imaging method based on multiple measurement vectors model[J]. Remote Sensing, 2017, 9(3): 297. doi: 10.3390/rs9030297 TIPPING M E and FAUL A. Fast marginal likelihood maximisation for sparse Bayesian models[C]. The 9th International Workshop on Artificial Intelligence and Statistics, Key West, USA, 2003: 3–6. WIPF D P and RAO B D. An empirical bayesian strategy for solving the simultaneous sparse approximation problem[J]. IEEE Transactions on Signal Processing, 2007, 55(7): 3704–3716. doi: 10.1109/tsp.2007.894265 ZHANG Zhilin and RAO B D. Sparse signal recovery in the presence of correlated multiple measurement vectors[C]. 2010 IEEE International Conference on Acoustics, Speech and Signal Processing, Dallas, USA, 2010: 3986–3989. doi: 10.1109/ICASSP.2010.5495780. ZHANG Zhilin and RAO B D. Iterative reweighted algorithms for sparse signal recovery with temporally correlated source vectors[C]. 2011 IEEE International Conference on Acoustics, Speech and Signal Processing, Prague, Czech Republic, 2011: 3932–3935. doi: 10.1109/ICASSP.2011.5947212. ZHANG Zhilin and RAO B D. Sparse signal recovery with temporally correlated source vectors using sparse Bayesian learning[J]. IEEE Journal of Selected Topics in Signal Processing, 2011, 5(5): 912–926. doi: 10.1109/JSTSP.2011.2159773 JI Shihao, DUNSON D, and CARIN L. Multitask compressive sensing[J]. IEEE Transactions on Signal Processing, 2009, 57(1): 92–106. doi: 10.1109/tsp.2008.2005866 ZHANG Zhilin and RAO B D. Extension of SBL algorithms for the recovery of block sparse signals with intra-block correlation[J]. IEEE Transactions on Signal Processing, 2013, 61(8): 2009–2015. doi: 10.1109/TSP.2013.2241055 BERNAL E A and LI Qun. Tensorial compressive sensing of jointly sparse matrices with applications to color imaging[C]. 2017 IEEE International Conference on Image Processing, Beijing, China, 2018: 2781–2785. doi: 10.1109/ICIP.2017.8296789. HAN Ningning and SONG Zhanjie. Bayesian multiple measurement vector problem with spatial structured sparsity patterns[J]. Digital Signal Processing, 2018, 75: 184–201. doi: 10.1016/j.dsp.2018.01.015 QIN Yanhua, LIU Yumin, and YU Zhongyuan. Underdetermined DOA estimation using coprime array via multiple measurement sparse Bayesian learning[J]. Signal, Image and Video Processing, 2019, 13(7): 1311–1318. doi: 10.1007/s11760-019-01480-x DU Yang, DONG Binhong, ZHU Wuyong, et al. Joint channel estimation and multiuser detection for uplink Grant-Free NOMA[J]. IEEE Wireless Communications Letters, 2018, 7(4): 682–685. doi: 10.1109/LWC.2018.2810278 SHAHIN S, SHAYEGH F, MORTAHEB S, et al. Improvement of flexible design matrix in sparse Bayesian learning for multi task fMRI data analysis[C]. The 23rd Iranian Conference on Biomedical Engineering and 20161st International Iranian Conference on Biomedical Engineering, Tehran, Iran, 2017: 3823–3826. doi: 10.1109/ICBME.2016.7890927. FENG Weike, GUO Yiduo, ZHANG Yongshun, et al. Airborne radar space time adaptive processing based on atomic norm minimization[J]. Signal Processing, 2018, 148: 31–40. doi: 10.1016/j.sigpro.2018.02.008 WU Jingjing, LI Siwei, ZHANG Saiwen, et al. Fast analysis method for stochastic optical reconstruction microscopy using multiple measurement vector model sparse Bayesian learning[J]. Optics Letters, 2018, 43(16): 3977–3980. doi: 10.1364/OL.43.003977 WIJEWARDHANA U L and CODREANU M. A Bayesian approach for online recovery of streaming signals from compressive measurements[J]. IEEE Transactions on Signal Processing, 2017, 65(1): 184–199. doi: 10.1109/TSP.2016.2614489 MALVAR H S and STAELIN D H. The LOT: Transform coding without blocking effects[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1989, 37(4): 553–559. doi: 10.1109/29.17536 BABIN S M, YOUNG G S, and CARTON J A. A new model of the oceanic evaporation duct[J]. Journal of Applied Meteorology, 1997, 36(3): 193–204. doi: 10.1175/1520-0450(1997)036<0193:ANMOTO>2.0.CO;2 -





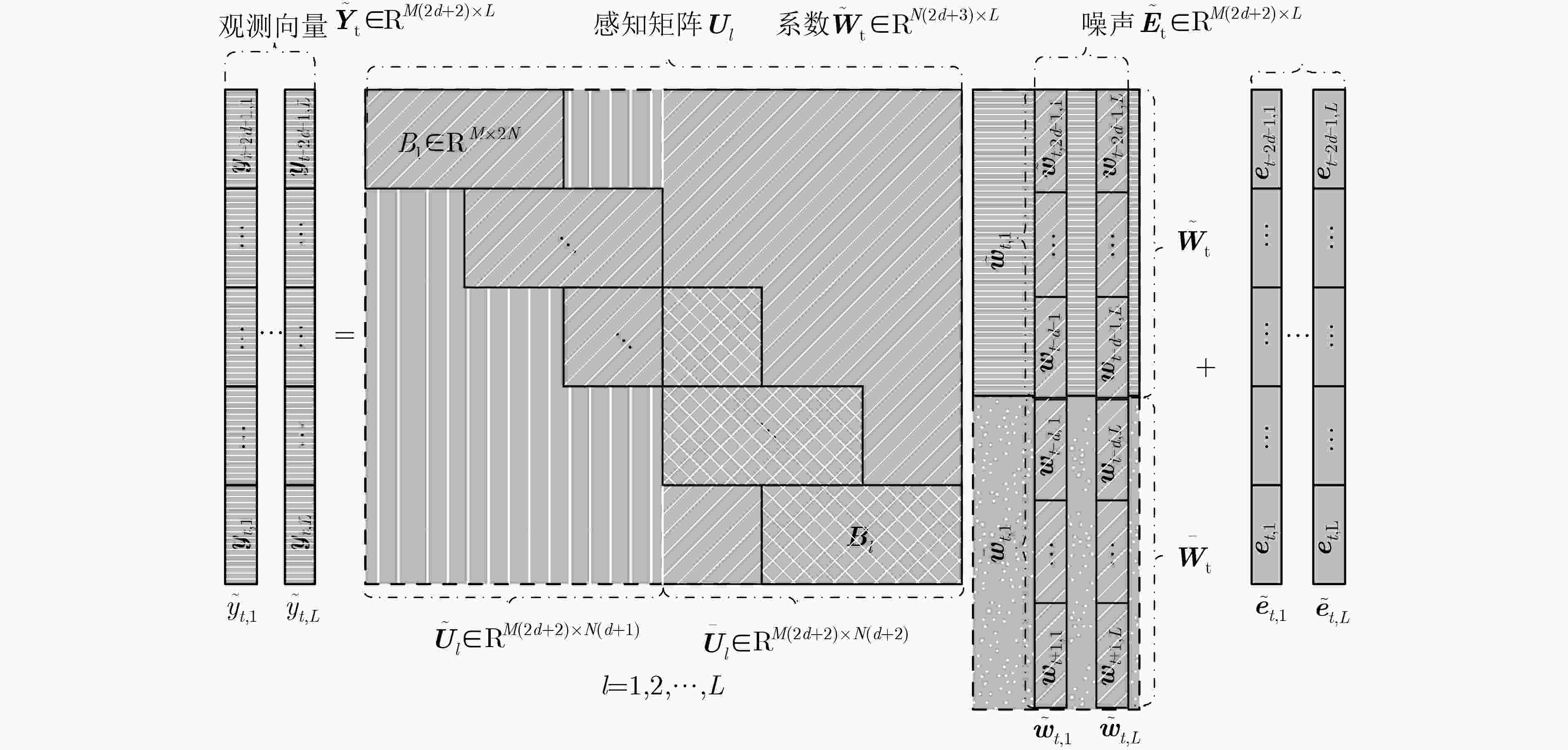
 下载:
下载:
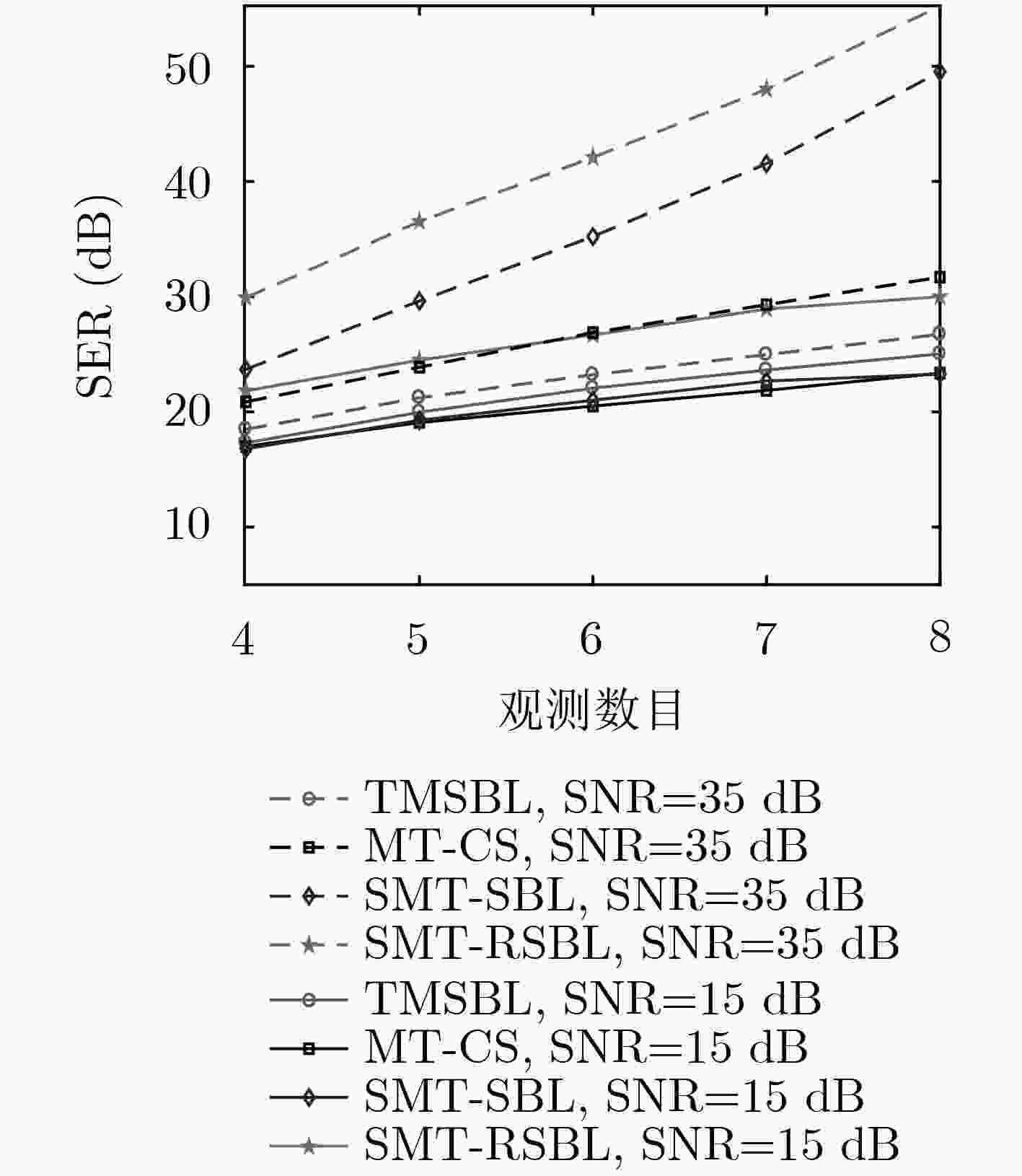
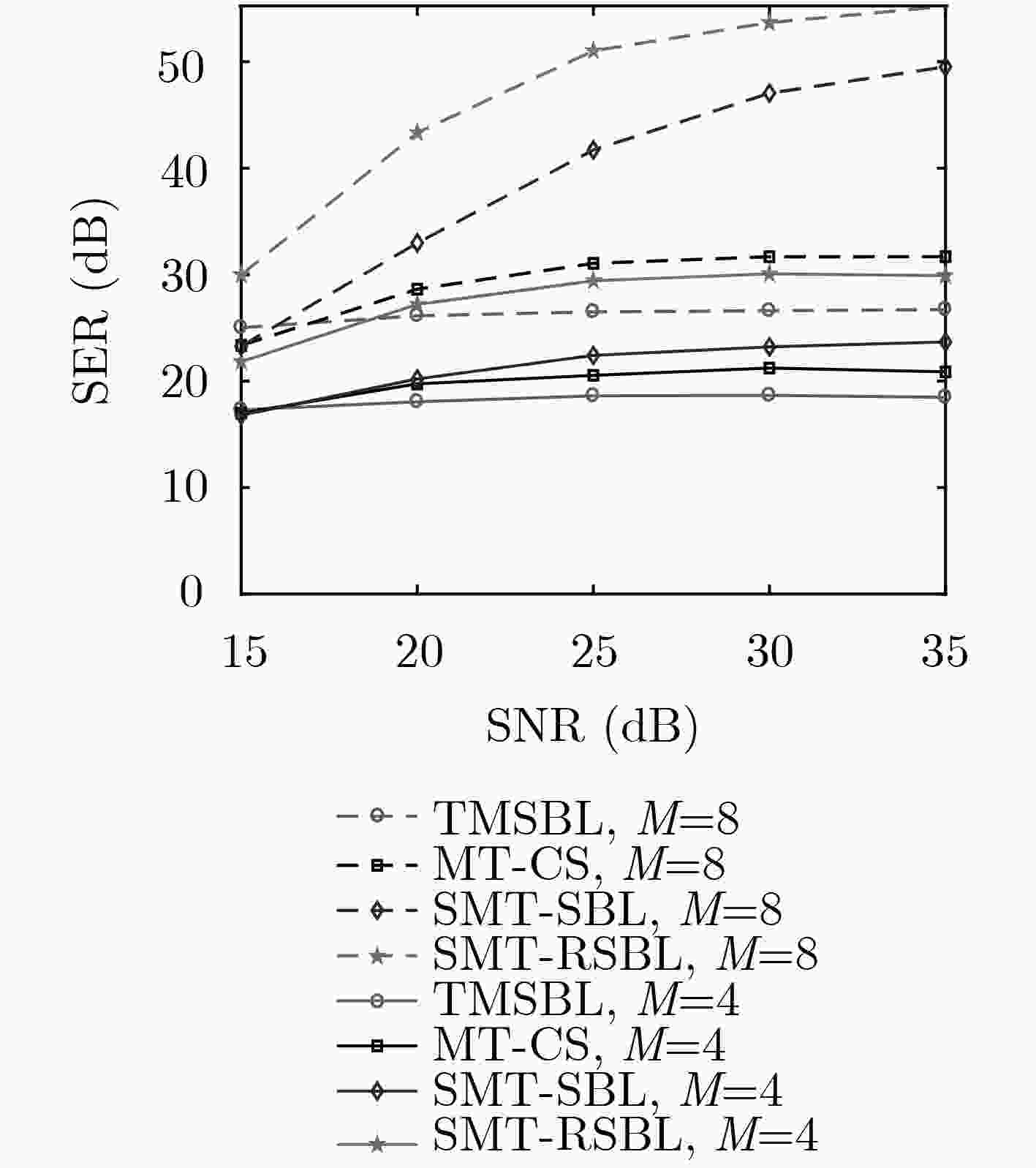
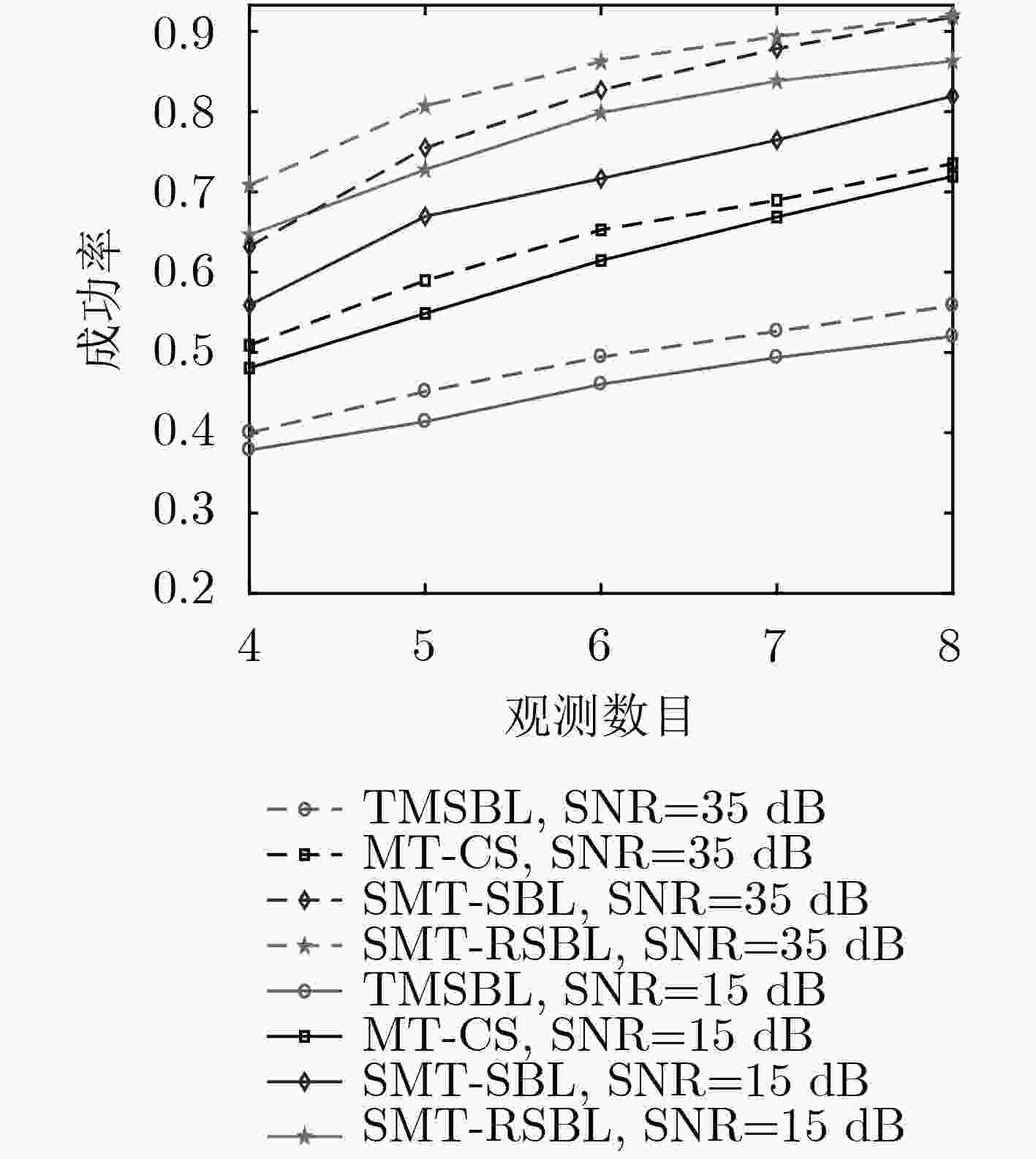


 下载:
下载:
