基于边信息改进的分布式信源编码方案

陈建华; 和志圆; 王炯

doi:10.11999/JEIT190522

基于边信息改进的分布式信源编码方案

doi: 10.11999/JEIT190522

云南大学信息学院电子工程系昆明 650500

基金项目: 国家自然科学基金(61861045)

详细信息

作者简介:
陈建华：男，1964年生，教授，博士生导师，研究方向为信息传输理论与应用

和志圆：男，1994年生，硕士生，研究方向为分布式信源编码

王炯：女，1994年生，硕士生，研究方向为Context建模

通讯作者:
陈建华　chenjh@ynu.edu.cn

中图分类号: TN911.21; TN919.81
计量
- 文章访问数: 2954
- HTML全文浏览量: 1192
- PDF下载量: 77
- 被引次数: 0
出版历程
- 收稿日期: 2019-07-11
- 修回日期: 2020-03-17
- 网络出版日期: 2020-04-15
- 刊出日期: 2020-07-23

Distributed Source Coding Using Improved Side Information

School of Information Science and Engineering, Yunnan University, Kunming 650500, China

Funds: The National Natural Science Foundation of China (61861045)

摘要

摘要:
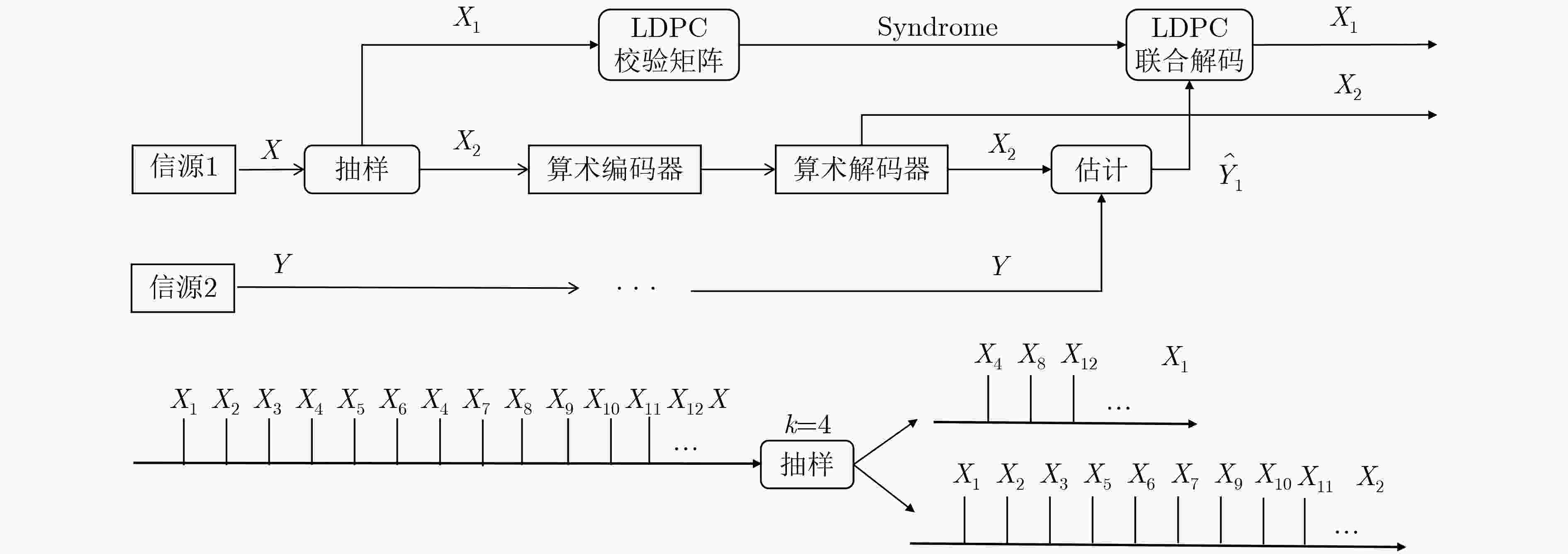
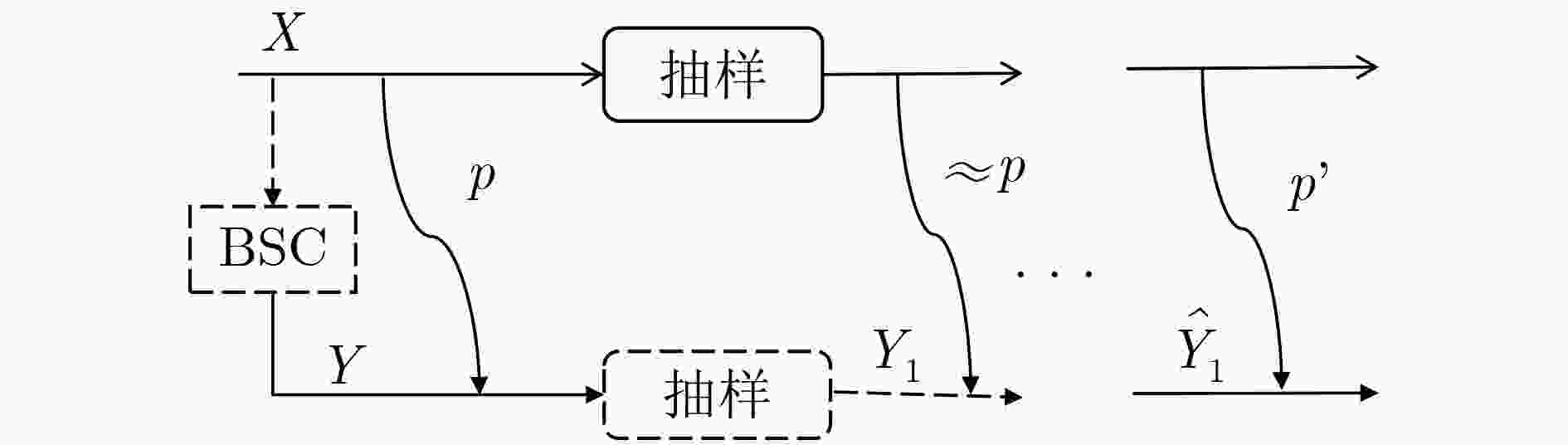
针对现有的非对称分布式信源编码(DSC)方案均存在的在误比特率(BER)以及压缩率方面的不足，该文提出基于边信息改进的DSC(DSCUISI)方案。发送方对信源序列进行抽样，将序列分为抽样与未抽样子序列，利用算术编码器对未抽样子序列进行压缩，同时计算抽样子序列的伴随式。接收方利用边信息序列与未抽样子序列之间的相关性，对抽样符号进行估计，估计出的序列与原始抽样子序列的相关性得到改进。最后利用原始抽样子序列的伴随式与估计出的序列进行联合译码以重建原始抽样子序列。实验结果表明：与基于低密度奇偶校验码和算术码的DSC方案相比，该文所提方案在信源内部相关性较强时具有压缩率高、在信源间相关度不高时则有重建错误率低的特点，是一种高效、实用且易于实现的DSC方案。
- 分布式信源编码 /
- 边信息 /
- 离散去噪理论 /
- 抽样
Abstract:
Considering the shortcomings on the Bit Error Rate (BER) and the compression ratio of the existing asymmetric Distributed Source Coding (DSC) schemes, a scheme named Distributed Source Coding Using Improved Side Information (DSCUISI) is proposed. At the sender, the source sequence is sampled and divided into a sampled and an un-sampled sub-sequences. The un-sampled sub-sequence is compressed by arithmetic coder while the syndrome of the sampled sub-sequence is calculated. The receiver exploits the correlation between the side information and the un-sampled sub-sequence to estimate the sampled symbols, so that the correlation between the estimated sequence and the original sampled sub-sequence is improved. Finally, the syndromes and the estimated sequence are used to recover the sampled sub-sequence. Experiment results show that the DSCUISI can reach high compression ratio, when the correlation among neighboring symbols is strong. The BER of the reconstructed sequence can be kept low when the correlation between sources are weak. It is an efficient, practical DSC scheme and is easy to be implemented.
- Distributed Source Coding(DSC) /
- Side Information(SI) /
- Discrete denoising theory /
- Sampling

HTML全文

图 1 DSCUISI方案以及抽样过程

下载: 全尺寸图片幻灯片

图 2 信源输出序列与SI序列相关性的变化

下载: 全尺寸图片幻灯片

图 3 条件点为被抽取点的解决方法

下载: 全尺寸图片幻灯片

图 4 文献[8]和文献[11]与DSCUISI的BER对比

下载: 全尺寸图片幻灯片

图 5 解码图像质量实验

下载: 全尺寸图片幻灯片

表 1 概率统计算法

输入：X and Y
Initialize count(00000)=1,…,count(11111)=1
Set i = 2 num=1
while (i<=N-1) do
if (i+1 mod k) = 0
count(X[i-1] 0 Y[i-1] Y[i+1] Y[i])++
count(X[i-1] 1 Y[i-1] Y[i+1] Y[i])++
else if (i mod k) = 0
continue
else if (i-1 mod k) = 0
count(0 X[i+1] Y[i-1] Y[i+1] Y[i])++
count(1 X[i+1] Y[i-1] Y[i+1] Y[i])++
else
count(X[i-1] X[i+1] Y[i-1] Y[i+1] Y[i])++
end if
end while
for num<=32
calculating probability using count
end for
输出：probability distribution

下载: 导出CSV

表 2 压缩率(码率)对比结果

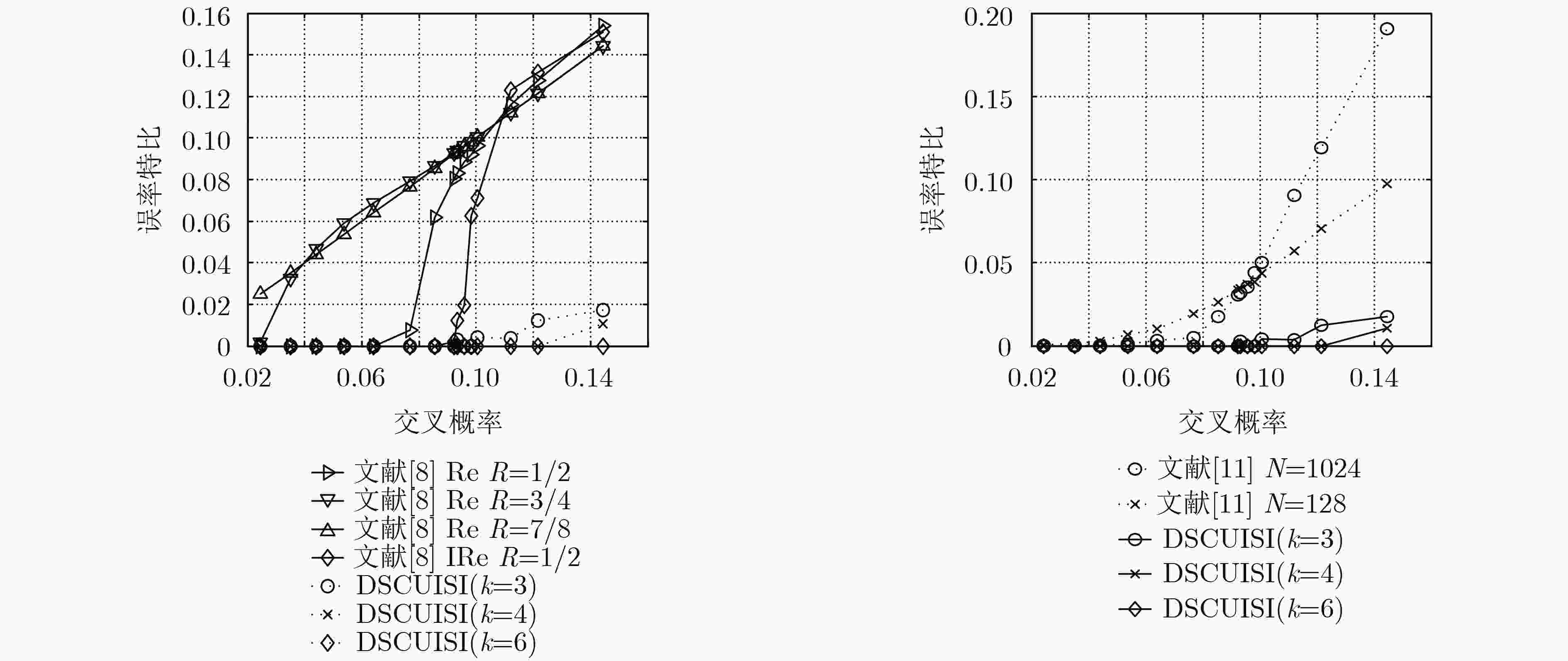
Peppers	p=0.0775, H(X\|Y)=0.3925			p=0.10759, H(X\|Y)=0.4918
	文献[8]BER : LDPC=0.0193; ILDPC=0			文献[8]BER : LDPC=0.1073; ILDPC=0.1158
	文献[11]: Rate=0.474487, BER=0.038486			文献[11]: Rate=0.474487, BER=0.150906
	C	DSCUISI方案的码率, k=3, k=4, k=6
	0	0.700040	0.727850		0.754701
	1	0.298285	0.274557		0.260146
	3	0.217124	0.203460		0.216251
Lena	p=0.076714, H(X\|Y)=0.3808			p=0.098148, H(X\|Y)=0.4516
	文献[8]BER : LDPC=0.0076; ILDPC=0			文献[8]BER : LDPC=0.0919; ILDPC=0.0625
	文献[11]: Rate=0.547241, BER=0.004826			文献[11]: Rate=0.547241, BER=0.043842
	C	DSCUISI方案的码率，k=3, k=4, k=6
	0	0.621454	0.61876		0.638811
	1	0.282116	0.255748		0.238359
	3	0.220430	0.201350		0.212461
Plane	p=0.080215, H(X\|Y)=0.3277			p=0.11145, H(X\|Y)=0.4048
	文献[8]BER : LDPC=0.0290; ILDPC=0			文献[8]BER : LDPC=0.1138; ILDPC=0.1238
	文献[11]: Rate=0.449249, BER=0.102680			文献[11]: Rate=0.449249, BER=0.148754
	C	DSCUISI方案的码率，k=3, k=4, k=6
	0	0.576643	0.593650		0.608581
	1	0.296949	0.279232		0.259157
	3	0.208356	0.205500		0.210581
Boats	p=0.076576, H(X\|Y)=0.3644			p=0.101559, H(X\|Y)=0.4403
	文献[8]BER : LDPC=0.0135; ILDPC=0			文献[8]BER : LDPC=0.0972; ILDPC=0.0899
	文献[11]: Rate=0.488861, BER=0.073799			文献[11]: Rate=0.488861, BER=0.145199
	C	DSCUISI方案的码率，k=3, k=4, k=6
	0	0.652294	0.678124		0.700619
	1	0.345531	0.321238		0.306967
	3	0.248442	0.246097		0.254241
Woman2	p=0.073326, H(X\|Y)=0.3630			p=0.102539, H(X\|Y)=0.4561
	文献[8]BER : LDPC=0.0029; ILDPC=0			文献[8]BER : LDPC=0.0996; ILDPC=0.1006
	文献[11]: Rate=0.523987, BER=0.009167			文献[11]: Rate=0.523987, BER=0.075237
	C	DSCUISI方案的码率，k=3, k=4, k=6
	0	0.582823	0.597651		0.608176
	1	0.230468	0.202129		0.179202
	3	0.174281	0.154635		0.150198

下载: 导出CSV

参考文献(17)

YANG Hong, QING Linbo, HE Xiaohai, et al. Robust distributed video coding for wireless multimedia sensor networks[J]. Multimedia Tools and Applications, 2018, 77(4): 4453–4475. doi: 10.1007/s11042-016-4245-x

YANG Jia, QING Linbo, ZENG Wenjun, et al. High-order statistical modeling based on a decision tree for distributed video coding[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2019, 29(5): 1488–1502. doi: 10.1109/TCSVT.2018.2840126

HAGAG A, FAN Xiaopeng, and EL-SAMIE F E A. Hyperspectral image coding and transmission scheme based on wavelet transform and distributed source coding[J]. Multimedia Tools and Applications, 2017, 76(22): 23757–23776. doi: 10.1007/s11042-016-4158-8

SLEPIAN D and WOLF J K. Noiseless coding of correlated information sources[J]. IEEE Transactions on Information Theory, 1973, 19(4): 471–480. doi: 10.1109/TIT.1973.1055037

洪少华, 王琳. 基于原模图LDPC码的分布式联合信源信道编码[J]. 电子与信息学报, 2017, 39(11): 2594–2599. doi: 10.11999/JEIT170113

HONG Shaohua and WANG Lin. Protograph LDPC based distributed joint source channel coding[J]. Journal of Electronics &Information Technology, 2017, 39(11): 2594–2599. doi: 10.11999/JEIT170113

PRADHAN S S and RAMCHANDRAN K. Distributed Source Coding Using Syndromes (DISCUS): Design and construction[J]. IEEE Transactions on Information Theory, 2003, 49(3): 626–643. doi: 10.1109/TIT.2002.808103

GARCIA-FRIAS J. Compression of correlated binary sources using turbo codes[J]. IEEE Communications Letters, 2001, 5(10): 417–419. doi: 10.1109/4234.957380

LIVERIS A D, XIONG Zixiang, and GEORGHIADES C N. Compression of binary sources with side information at the decoder using LDPC codes[J]. IEEE Communications Letters, 2002, 6(10): 440–442. doi: 10.1109/LCOMM.2002.804244

JIN Liqiang, YANG Pei, and YANG Hongwen. Distributed joint source-channel decoding using systematic polar codes[J]. IEEE Communications Letters, 2018, 22(1): 49–52. doi: 10.1109/LCOMM.2017.2768036

GRANGETTO M, MAGLI E, and OLMO G. Distributed arithmetic coding[J]. IEEE Communications Letters, 2007, 11(11): 883–885. doi: 10.1109/LCOMM.2007.071172

GRANGETTO M, MAGLI E, and OLMO G. Distributed arithmetic coding for the Slepian-Wolf problem[J]. IEEE Transactions on Signal Processing, 2009, 57(6): 2245–2257. doi: 10.1109/TSP.2009.2014280

MALINOWSKI S, ARTIGAS X, GUILLEMOT C, et al. Distributed coding using punctured quasi-arithmetic codes for memory and memoryless sources[J]. IEEE Transactions on Signal Processing, 2009, 57(10): 4154–4158. doi: 10.1109/TSP.2009.2023359

CAO Ying, SUN Lijuan, HAN Chong, et al. Improved side information generation algorithm based on naive Bayesian theory for distributed video coding[J]. IET Image Processing, 2018, 12(3): 354–360. doi: 10.1049/iet-ipr.2017.0892

DASH B, RUP S, MOHAPATRA A, et al. Decoder driven side information generation using ensemble of MLP networks for distributed video coding[J]. Multimedia Tools and Applications, 2018, 77(12): 15221–15250. doi: 10.1007/s11042-017-5103-1

VARODAYAN D, LIN Y C, GIROD B, et al. Adaptive distributed source coding[J]. IEEE Transactions on Image Processing, 2012, 21(5): 2630–2640. doi: 10.1109/TIP.2011.2175936

罗瑜, 张珍珍. 一种方向插值预测变长编码的帧存有损压缩算法[J]. 电子与信息学报, 2019, 41(10): 2495–2500. doi: 10.11999/JEIT181195

LUO Yu and ZHANG Zhenzhen. A lossy frame memory compression algorithm using directional interpolation prediction variable length coding[J]. Journal of Electronics &Information Technology, 2019, 41(10): 2495–2500. doi: 10.11999/JEIT181195

WEISSMAN T, ORDENTLICH E, SEROUSSI G, et al. Universal discrete denoising: Known channel[J]. IEEE Transactions on Information Theory, 2005, 51(1): 5–28. doi: 10.1109/TIT.2004.839518

施引文献

资源附件(0)

访问统计