Design and Implementation of Cyclic Redundancy Check with Variable Computing Width Based on Formula Recursive Algorithm
-
摘要:
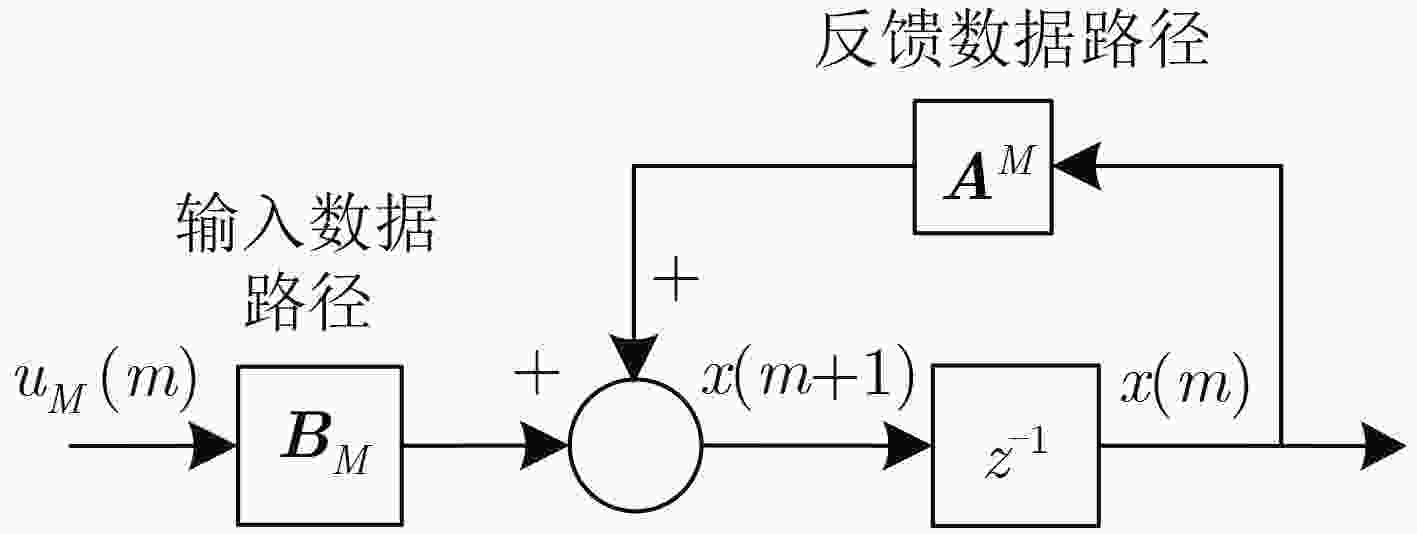
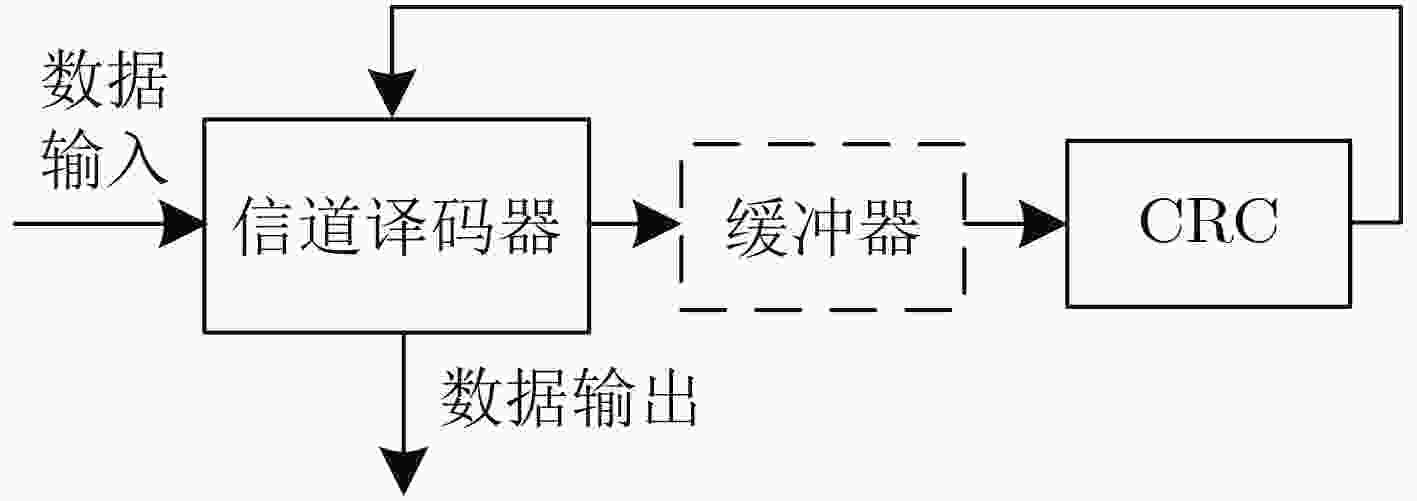
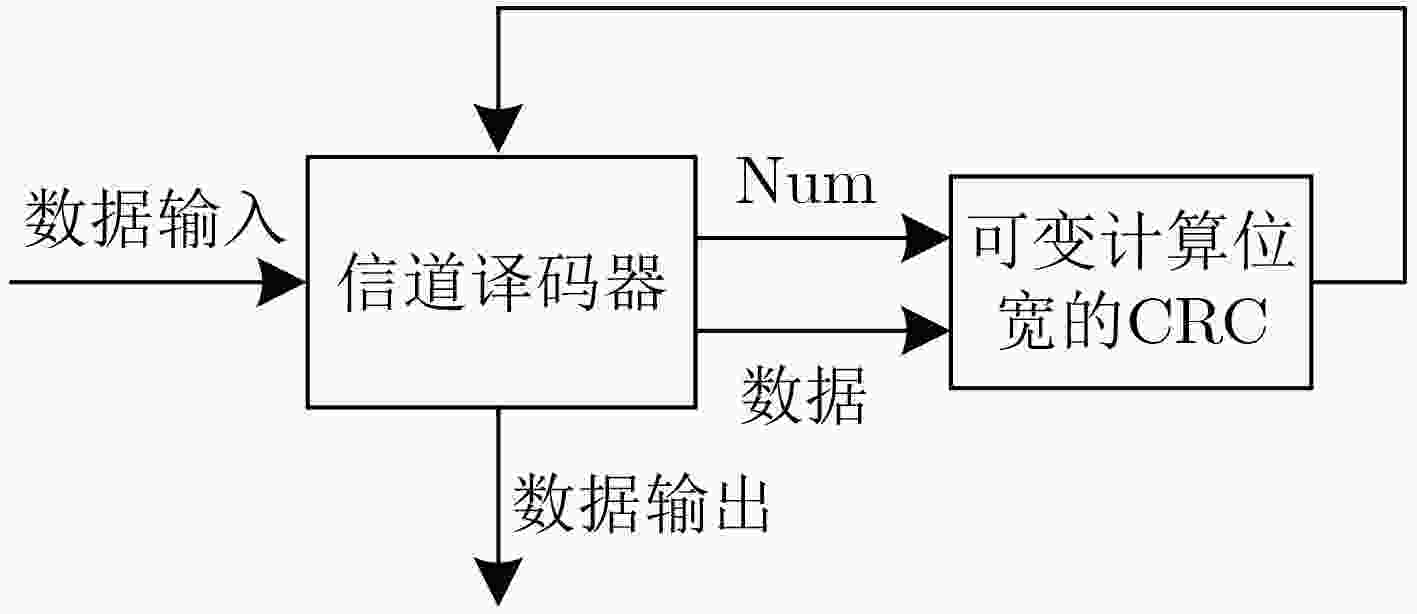
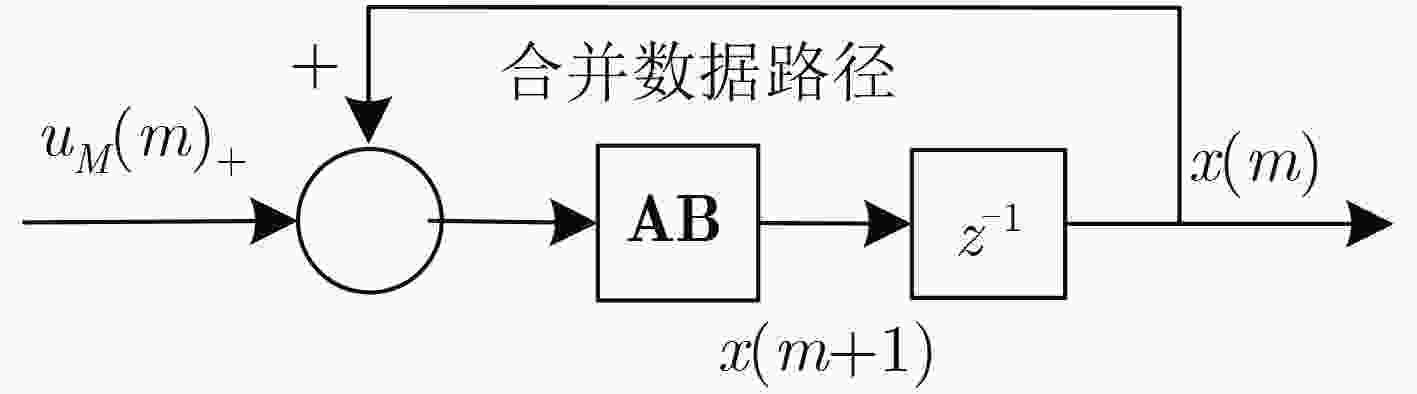
循环冗余校验(CRC)与信道编码的级联使用,可以有效改善译码的收敛特性。在新一代无线通信系统,如5G中,码长和码率都具有多样性。为了提高编译码分段长度可变的级联系统的译码效率,该文提出一种可变计算位宽的CRC并行算法。该算法在现有固定位宽并行算法的基础上,合并公式递推法中反馈数据与输入数据的并行计算,实现了一种高并行度的CRC校验架构,并且支持可变位宽的CRC计算。与现有的并行算法相比,合并算法节省了电路资源的开销,在位宽固定时,资源节约效果明显,同时在反馈时延上也有将近50%的优化;在位宽可变时,电路资源的使用情况也有相应的优化。
Abstract:Cyclic Redundancy Check (CRC) is used in cascade with channel coding to improve the convergence of the decoding. In the new generation of wireless communication systems, such as 5G, both code length and code rate are diverse. To improve the decoding efficiency of cascaded systems, a CRC parallel algorithm with variable computing width is proposed in this paper. Based on the existing fixed bit-width parallel algorithm, this algorithm combines the parallel calculation of feedback data and input data in the formula recursive method, realizing a highly parallel CRC check architecture with variable bit-width CRC calculation. Compared with the existing parallel algorithms, the merged algorithm saves the overhead of circuit resources. When the bit-width is fixed, the resource saving effect is obvious, and at the same time, the feedback delay is also optimized by nearly 50%. When the bit-width is variable, the use of resources is also optimized accordingly.
-
表 1 硬件资源开销
项目 值 顶层实体名 crc_24 芯片 EP3C5E144C7(Cyclone III) 逻辑器件数 434/5136(8%) 寄存器数 26 管脚数 68/95(72%) 表 2 仿真测试结果
总长度
(bit)Num Matlab结果 仿真结果 数据1 60 7, 24, 29 001111010110111111110110 24’h3d6ff6 数据2 65 23, 32, 10 001110000010011011010001 24’h3826d1 数据3 70 24, 15, 31 011111100000011111011011 24’h7e07db 表 3 选用的生成多项式
CRC 生成多项式 CRC-12 ${x^{12}} + {x^{11}} + {x^3} + {x^2} + x + 1$ CRC-16 ${x^{16}} + {x^{15}} + {x^2} + 1$ CRC-32 $\begin{array}{l}{x^{32}} + {x^{26}} + {x^{23}} + {x^{22}} + {x^{16}} + {x^{12}} + {x^{11}} + \\{x^{10}} + {x^8} + {x^7} + {x^5} + {x^4} + {x^2} + x + 1\end{array}$ 表 4 电路资源和关键路径长度比较
CRC式子(M=r) 算法 总计 1 异或 关键路径 CRC-12(12) 文献[7] 136 112 9 文献[8] 120 66 8 文献[10] – 103 8 文献[9] 77 53 8 固定 52 43 5 可变 64 78 9 CRC-16(16) 文献[7] 218 186 10 文献[8] 188 98 10 文献[10] – 94 10 文献[9] 100 60 9 固定 72 54 5 可变 88 101 9 CRC-32(32) 文献[7] 1031 967 12 文献[8] 928 518 12 文献[10] – 675 10 文献[9] 888 461 12 固定 452 313 6 可变 484 408 11 -
LI Bin, HUANG Zhiping, SU Shaojing, et al. Implementation of CRC in 10-gigabit Ethernet based on FPGA[J]. Applied Mechanics and Materials, 2014, 599–601: 1548–1552. doi: 10.4028/www.scientific.net/AMM.599-601.1548 WANG Bingrui, CHEN Pingping, FANG Yi, et al. The design of vertical RS-CRC and LDPC code for ship-based satellite communications on-the-move[J]. IEEE Access, 2019, 7: 44977–44986. doi: 10.1109/ACCESS.2019.2895746 CAMPOBELLO G, PATANE G, and RUSSO M. Parallel CRC realization[J]. IEEE Transactions on Computers, 2003, 52(10): 1312–1319. doi: 10.1109/TC.2003.1234528 MUTHIAH D and RAJ A A B. Implementation of high-speed LFSR design with parallel architectures[C]. 2012 International Conference on Computing, Communication and Applications, Dindigul, India, 2012: 1–6. HUO Yuanhong, LI Xiaoyang, WANG Wei, et al. High performance table-based architecture for parallel CRC calculation[C]. The 21st IEEE International Workshop on Local and Metropolitan Area Networks, Beijing, 2015: 1–6. BAJARANGBALI and ANAND P A. Design of high speed CRC algorithm for ethernet on FPGA using reduced lookup table algorithm[C]. 2016 IEEE Annual India Conference, Bangalore, India, 2016: 1–6. DERBY J H. High-speed CRC computation using state-space transformations[C]. GLOBECOM’01. IEEE Global Telecommunications Conference, San Antonio, USA, 2001: 166–170. KENNEDY C and REYHANI-MASOLEH A. High-speed CRC computations using improved state-space transformations[C]. 2009 IEEE International Conference on Electro/Information Technology, Windsor, Canada, 2009: 9–14. HU Guanghui, SHA Jin, and WANG Zhongfeng. High-speed parallel LFSR architectures based on improved state-space transformations[J]. IEEE Transactions on Very Large Scale Integration (VLSI) Systems, 2017, 25(3): 1159–1163. doi: 10.1109/TVLSI.2016.2608921 JUNG J, YOO H, LEE Y, et al. Efficient parallel architecture for linear feedback shift registers[J]. IEEE Transactions on Circuits and Systems Ⅱ: Express Briefs, 2015, 62(11): 1068–1072. doi: 10.1109/tcsii.2015.2456294 CHENG Chao and PARHI K K. High-speed parallel CRC implementation based on unfolding, pipelining, and retiming[J]. IEEE Transactions on Circuits and Systems Ⅱ: Express Briefs, 2006, 53(10): 1017–1021. doi: 10.1109/TCSⅡ.2006.882213 AYINALA M and PARHI K K. High-speed parallel architectures for linear feedback shift registers[J]. IEEE Transactions on Signal Processing, 2011, 59(9): 4459–4469. doi: 10.1109/TSP.2011.2159495 李伟华, 焦秉立. 一种基于分段CRC的LDPC译码的改进算法[J]. 电子与信息学报, 2008, 30(5): 1167–1170. doi: 10.3724/SP.J.1146.2006.01763LI Weihua and JIAO Bingli. Improved method for LDPC decoding algorithm aided by segmented cyclic redundancy checks[J]. Journal of Electronics &Information Technology, 2008, 30(5): 1167–1170. doi: 10.3724/SP.J.1146.2006.01763 TUSHA A, DOĞAN S, and ARSLAN H. IQI mitigation for narrowband IoT systems with OFDM-IM[J]. IEEE Access, 2018, 6: 44626–44634. doi: 10.1109/ACCESS.2018.2864892 VAN WONTERGHEM J, ALLOUM A, BOUTROS J J, et al. On short-length error-correcting codes for 5G-NR[J]. Ad Hoc Networks, 2018, 79: 53–62. doi: 10.1016/j.adhoc.2018.06.005 RICHARDSON T and KUDEKAR S. Design of low-density parity check codes for 5G new radio[J]. IEEE Communications Magazine, 2018, 56(3): 28–34. doi: 10.1109/MCOM.2018.1700839 王琼, 罗亚洁, 李思舫. 基于分段循环冗余校验的极化码自适应连续取消列表译码算法[J]. 电子与信息学报, 2019, 41(7): 1572–1578. doi: 10.11999/JEIT180716WANG Qiong, LUO Yajie, and LI Sifang. Polar adaptive successive cancellation list decoding based on segmentation cyclic redundancy check[J]. Journal of Electronics &Information Technology, 2019, 41(7): 1572–1578. doi: 10.11999/JEIT180716 -






 下载:
下载:



 下载:
下载:
