A Batch Inheritance Extreme Learning Machine Algorithm Based on Regular Optimization
-
摘要:
极限学习机(ELM)作为一种新型神经网络,具有极快的训练速度和良好的泛化性能。针对极限学习机在处理高维数据时计算复杂度高,内存需求巨大的问题,该文提出一种批次继承极限学习机(B-ELM)算法。首先将数据集均分为不同批次,采用自动编码器网络对各批次数据进行降维处理;其次引入继承因子,建立相邻批次之间的关系,同时结合正则化框架构建拉格朗日优化函数,实现批次极限学习机数学建模;最后利用MNIST, NORB和CIFAR-10数据集进行测试实验。实验结果表明,所提算法具有较高的分类精度,并且有效降低了计算复杂度和内存消耗。
Abstract:As a new type of neural network, Extreme Learning Machine (ELM) has extremely fast training speed and good generalization performance. Considering the problem that the Extreme Learning Machine has high computational complexity and huge memory demand when dealing with high dimensional data, a Batch inheritance Extreme Learning Machine (B-ELM) algorithm is proposed. Firstly, the dataset is divided into different batches, and the automatic encoder network is used to reduce the dimension of each batch. Secondly, the inheritance factor is introduced to establish the relationship between adjacent batches. At the same time, the Lagrange optimization function is constructed by combining the regularization framework to realize the mathematical modeling of batch ELM. Finally, the MNIST, NORB and CIFAR-10 datasets are used for the test experiment. The experimental results show that the proposed algorithm not only has higher classification accuracy, but also reduces effectively computational complexity and memory consumption.
-
表 1 不同数据集上的性能比较
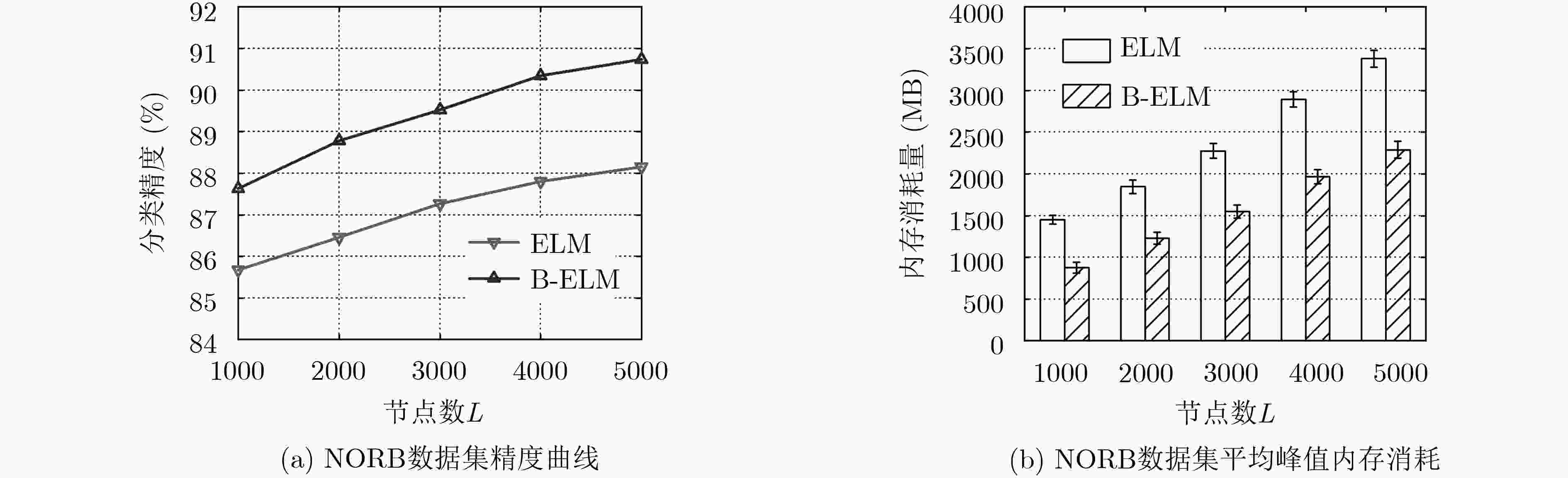
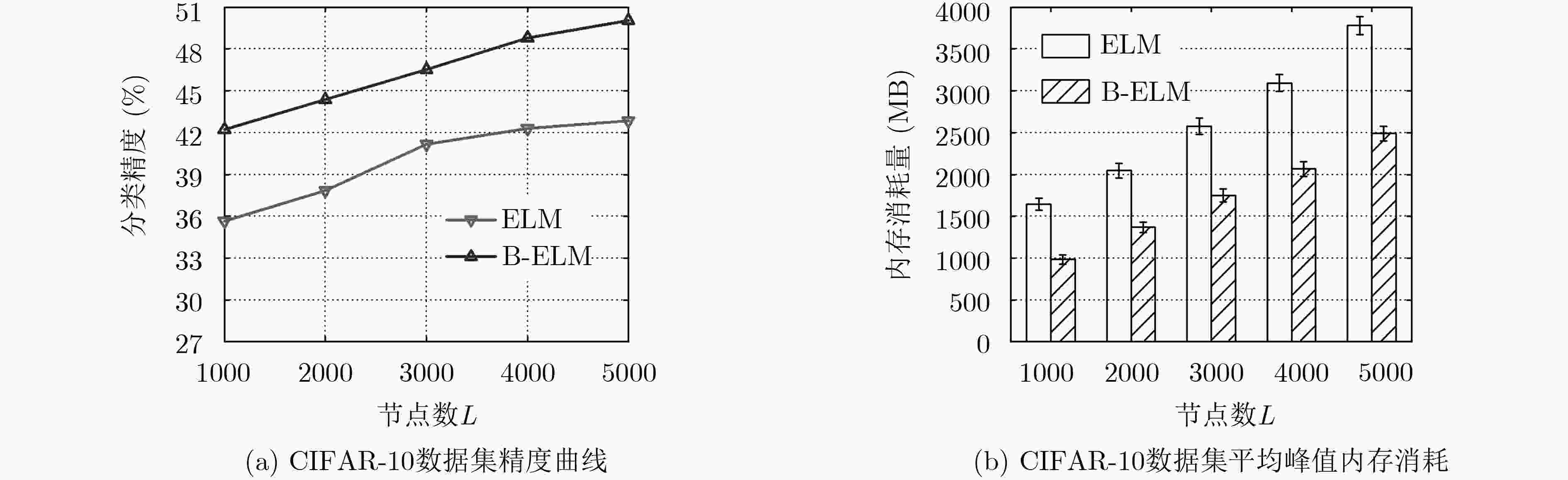
分类方法 MNIST NORB CIFAR-10 精度(%) 训练时间(s) 精度(%) 训练时间(s) 精度(%) 训练时间(s) SAE 98.60 4042.36 86.28 6438.56 43.37 60514.26 SDA 98.72 3892.26 87.62 6572.14 43.61 87289.59 DBM 99.05 14505.14 89.65 18496.64 43.12 90123.53 ML-ELM 98.21 51.83 88.91 78.36 45.42 74.06 H-ELM 99.12 28.97 91.28 42.74 50.21 62.76 B-ELM 99.43 42.67 91.90 55.96 50.38 69.06 -
HUANG Guangbin, ZHU Qinyu, and SIEW C K. Extreme learning machine: Theory and applications[J]. Neurocomputing, 2006, 70(1/3): 489–501. doi: 10.1016/j.neucom.2005.12.126 李佩佳, 石勇, 汪华东, 等. 基于有序编码的核极限学习顺序回归模型[J]. 电子与信息学报, 2018, 40(6): 1287–1293. doi: 10.11999/JEIT170765LI Peijia, SHI Yong, WANG Huadong, et al. Ordered code-based kernel extreme learning machine for ordinal regression[J]. Journal of Electronics &Information Technology, 2018, 40(6): 1287–1293. doi: 10.11999/JEIT170765 HUANG Guangbin, ZHOU Hongming, DING Xiaojian, et al. Extreme learning machine for regression and multiclass classification[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics) , 2012, 42(2): 513–529. doi: 10.1109/tsmcb.2011.2168604 WANG Yongchang and ZHU Ligu. Research and implementation of SVD in machine learning[C]. The 2017 16th IEEE/ACIS International Conference on Computer and Information Science, Wuhan, China, 2017: 471–475. doi: 10.1109/ICIS.2017.7960038. CASTAÑO A, FERNÁNDEZ-NAVARRO F, and HERVÁS-MARTÍNEZ C. PCA-ELM: A robust and pruned extreme learning machine approach based on principal component analysis[J]. Neural Processing Letters, 2013, 37(3): 377–392. doi: 10.1007/s11063-012-9253-x ZONG Weiwei, HUANG Guangbin, and CHEN Yiqiang. Weighted extreme learning machine for imbalance learning[J]. Neurocomputing, 2013, 101: 229–242. doi: 10.1016/j.neucom.2012.08.010 ZHAO Rui and MAO Kezhi. Semi-random projection for dimensionality reduction and extreme learning machine in high-dimensional space[J]. IEEE Computational Intelligence Magazine, 2015, 10(3): 30–41. doi: 10.1109/MCI.2015.2437316 LUO Xiong, XU Yang, WANG Weiping, et al. Towards enhancing stacked extreme learning machine with sparse autoencoder by correntropy[J]. Journal of the Franklin Institute, 2018, 355(4): 1945–1966. doi: 10.1016/j.jfranklin.2017.08.014 WU Shuang, LI Guoqi, DENG Lei, et al. L1-norm batch normalization for efficient training of deep neural networks[J]. IEEE Transactions on Neural Networks and Learning Systems, 2019, 30(7): 2043–2051. doi: 10.1109/TNNLS.2018.2876179 LI Yanghao, WANG Naiyan, SHI Jianping, et al. Adaptive batch normalization for practical domain adaptation[J]. Pattern Recognition, 2018, 80: 109–117. doi: 10.1016/j.patcog.2018.03.005 LIANG Nanying, HUANG Guangbin, SARATCHANDRAN P, et al. A fast and accurate online sequential learning algorithm for feedforward networks[J]. IEEE Transactions on Neural Networks, 2006, 17(6): 1411–1423. doi: 10.1109/TNN.2006.880583 HUANG Guangbin. What are extreme learning machines? Filling the gap between frank Rosenblatt’s dream and john von Neumann’s puzzle[J]. Cognitive Computation, 2015, 7(3): 263–278. doi: 10.1007/s12559-015-9333-0 YI Yugen, QIAO Shaojie, ZHOU Wei, et al. Adaptive multiple graph regularized semi-supervised extreme learning machine[J]. Soft Computing, 2018, 22(11): 3545–3562. doi: 10.1007/s00500-018-3109-x CHENG Kai and LU Zhenzhou. Adaptive sparse polynomial chaos expansions for global sensitivity analysis based on support vector regression[J]. Computers & Structures, 2018, 194: 86–96. doi: 10.1016/j.compstruc.2017.09.002 HINTON G E and SALAKHUTDINOV R R. Reducing the dimensionality of data with neural networks[J]. Science, 2006, 313(5786): 504–507. doi: 10.1126/science.1127647 VINCENT P, LAROCHELLE H, BENGIO Y, et al. Extracting and composing robust features with denoising autoencoders[C]. The 25th International Conference on Machine Learning, Helsinki, Finland, 2008: 1096–1103. doi: 10.1145/1390156.1390294. SALAKHUTDINOV R and HINTON G. An efficient learning procedure for deep Boltzmann machines[J]. Neural Computation, 2012, 24(8): 1967–2006. doi: 10.1162/NECO_a_00311 CAMBRIA E, HUANG Guangbin, KASUN L L C, et al. Extreme learning machines[trends & controversies][J]. IEEE Intelligent Systems, 2013, 28(6): 30–59. doi: 10.1109/MIS.2013.140 TANG Jiexiong, DENG Chenwei, and HUANG Guangbin. Extreme learning machine for multilayer perceptron[J]. IEEE Transactions on Neural Networks and Learning Systems, 2016, 27(4): 809–821. doi: 10.1109/TNNLS.2015.2424995 -





 下载:
下载:




 下载:
下载:
