Energy Efficient Power Allocation with NOMA in Downlink Heterogeneous Networks
-
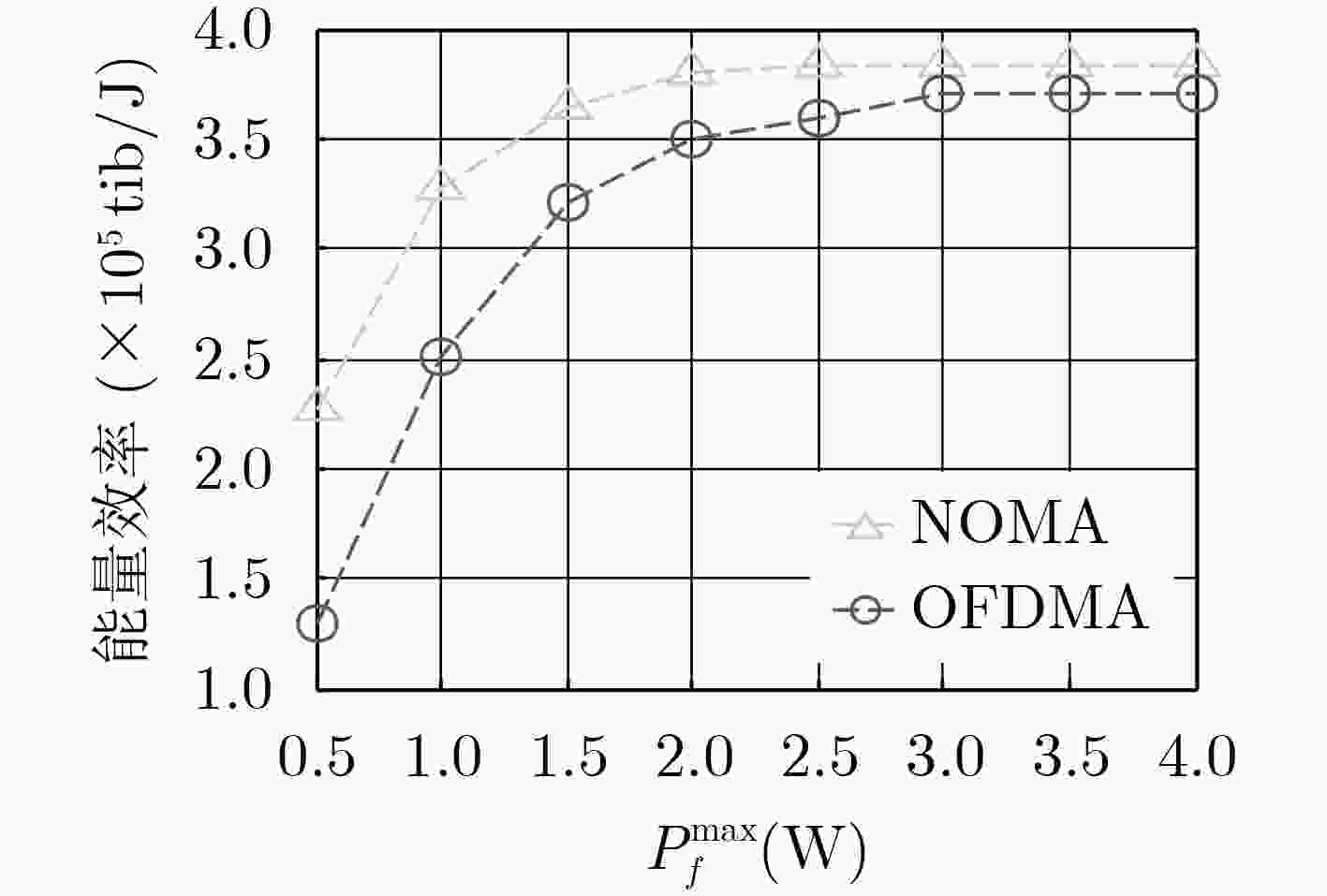
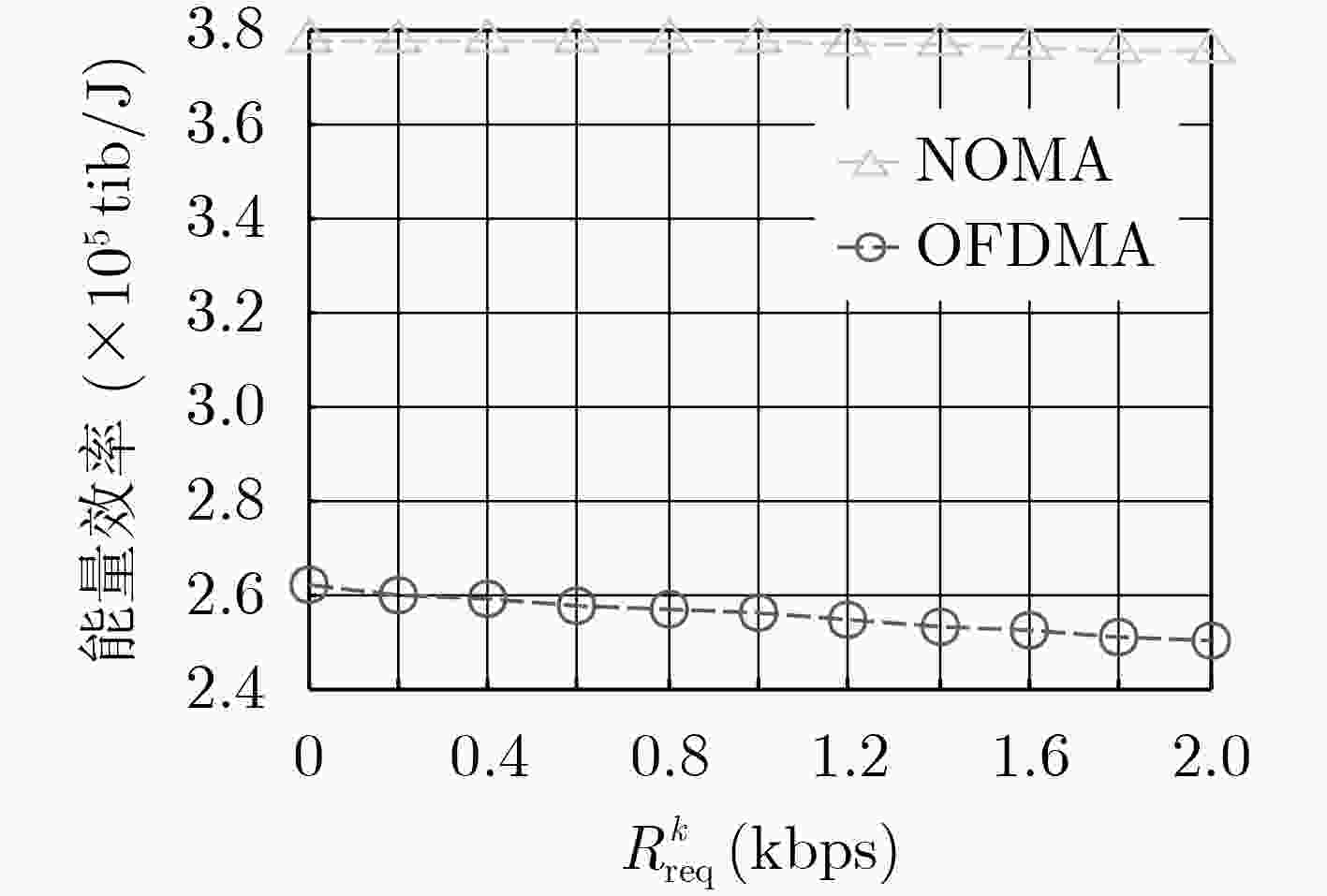
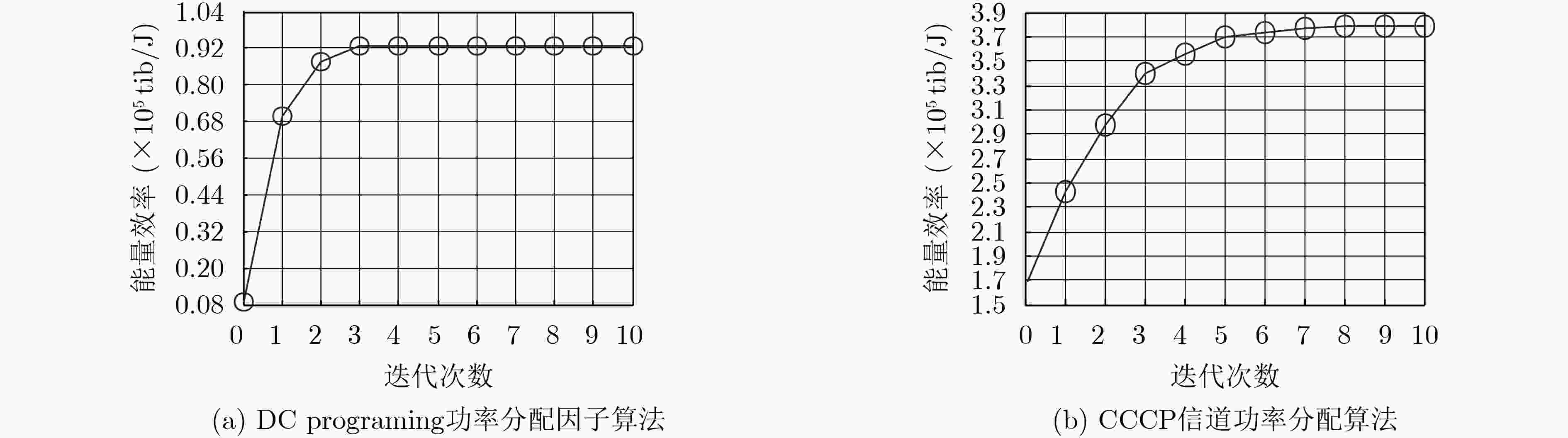
摘要: 该文针对应用非正交多址接入(NOMA)技术的异构蜂窝网络,在考虑层间层内干扰的情况下,提出一种能效最大化的功率分配算法。该算法主要包括两部分,一部分为子信道内用户功率分配因子的求解,主要利用差分优化的方法,迭代求解。另一部分为子信道间的功率分配,主要利用凹凸程序法将原有的非凸问题简化为可解的凸问题,最后利用拉格朗日求解法得出功率最优解。仿真结果表明该算法有良好的迭代性,且新算法表明利用NOMA技术得到的系统能效较利用正交技术得到的系统能效提高了至少44%以上。Abstract: This paper proposes a power allocation scheme for energy efficiency maximization in a downlink Non-Orthogonal Multiple Access (NOMA)-based Heterogeneous Network (HetNets) with considering the out-of-cell interference and in-cell interference. The scheme contains mainly two parts. One is the power allocation between the users at the same sub-channel, where Difference of Convex (DC) functions -programming is exploited to solve the problem. Another is the power allocation between the sub-channels, in which ConCave–Convex Procedure (CCCP) method and Lagrangian multiplier method are combined to solve the problem. The simulation results show that the fast convergence property, and demonstrate that the EE obtained by the proposed algorithms based on NOMA is at least 44% higher than that obtained by the conventional orthogonal multiple access scheme.
-
表 1 子信道内用户功率分配因子算法
DC programing功率分配因子算法 1.初始化:设置${(\alpha _f^n)^c}$的初始值;设置迭代索引$c = 0$;设置最大迭代次数${C_{\max }}$以及容忍度$\mu $的值;计算式
$q({(\alpha _f^n)^0}) = f({(\alpha _f^n)^0}) - g({(\alpha _f^n)^0})$的值。2. repeat 3. 计算式(8)获取最优功率分配因子${(\alpha _f^n)^*}$ 4. $c = c + 1$,${(\alpha _f^n)^c} = {(\alpha _f^n)^*}$,计算$q({(\alpha _f^n)^c}) = f({(\alpha _f^n)^c}) - g({(\alpha _f^n)^c})$ 5. until $\left| {q({{(\alpha _f^n)}^c}) - q({{(\alpha _f^n)}^{c - 1}})} \right| \le \mu $ or $c > {C_{\max }}$ 6. ${(\alpha _f^n)^*} = {(\alpha _f^n)^c}$ 表 2 子信道间功率分配算法
CCCP信道功率分配算法 1:初始化 设置迭代索引$v = 0$,误差容忍度$\xi > 0$。设置初始化${{{P}}^0}$,最大迭代次数${V_{\max }}$,计算${\left( {\lambda _f^n} \right)^0} = {1 / {\left( {{{\left( {p_f^n} \right)}^0} + {p_c}} \right)}}$,
${(\gamma _f^n)^0} = {{R_f^n\left( {{{(p_f^n)}^0}} \right)} / {\left( {{{(p_f^n)}^0} + {p_c}} \right)}}$2: repeat 3:利用拉格朗日对偶求解${\left( {{{{P}}^*}} \right)^v}$即${{{P}}^{v + 1}}$其中${\left( {{{{P}}^*}} \right)^v}$满足式(35)和式(36)。 4:根据式(12)更新${(\lambda _f^n)^{v + 1}}$和${(\gamma _f^n)^{v + 1}}$的值。 5:设置$v = v + 1$
6: until $\left| {\mathop {\max }\limits_{{P} } \left\{ {\displaystyle\sum\limits_{f = 1}^F { { {(\lambda _f^n)}^v}[R_f^n({ {(p_f^n)}^v})(1 + { {\beta \left( { { {(p_f^n)}^v} + {p_c} } \right)} / B}) - { {(\gamma _f^n)}^v}({ {(p_f^n)}^v} + {p_c})]} } \right\} } \right| \le \xi$ or $v > {V_{\max }}$ -
DAMNJANOVIC A, MONTOJO J, WEI Yongbin, et al. A survey on 3GPP heterogeneous networks[J]. IEEE Wireless Communications, 2011, 18(3): 10–21. doi: 10.1109/MWC.2011.5876496 DAI Linglong, WANG Bichai, DING Zhiguo, et al. A survey of non-orthogonal multiple access for 5G[J]. IEEE Communications Surveys & Tutorials, 2018, 20(3): 2294–2323. doi: 10.1109/COMST.2018.2835558 FANG Fang, CHENG Julian, and DING Zhiguo. Joint energy efficient subchannel and power optimization for a downlink NOMA heterogeneous network[J]. IEEE Transactions on Vehicular Technology, 2019, 68(2): 1351–1364. doi: 10.1109/TVT.2018.2881314 MOKDAD A, AZMI P, and MOKARI N. Radio resource allocation for heterogeneous traffic in GFDM-NOMA heterogeneous cellular networks[J]. IET Communications, 2016, 10(12): 1444–1455. doi: 10.1049/iet-com.2016.0011 SONG Zhengyu, NI Qiang, and SUN Xin. Distributed power allocation for nonorthogonal multiple access heterogeneous networks[J]. IEEE Communications Letter, 2018, 22(3): 622–625. doi: 10.1109/LCOMM.2017.2789282 NASSER A, MUTA O, ELSABROUTY M, et al. Compressive sensing based spectrum allocation and power control for NOMA HetNets[J]. IEEE Access, 2019, 7: 98495–98506. doi: 10.1109/ACCESS.2019.2929185 NI Dadong, HAO Li, TRAN Q T, et al. Power allocation for downlink NOMA heterogeneous networks[J]. IEEE Access, 2018, 6: 26742–26752. doi: 10.1109/ACCESS.2018.2835568 STEFANO B, CHIH L I, THIERR Y E, et al. A survey of energy-efficient techniques for 5G networks and challenges ahead[J]. IEEE Journal on Selected Areas in Communications, 2016, 34(4): 697–709. doi: 10.1109/JSAC.2016.2550338 QIN Zhijin, YUE Xinwei, LIU Yuanwei, et al. User association and resource allocation in unified NOMA enabled heterogeneous Ultra dense networks[J]. IEEE Communications Magazine, 2018, 56(6): 86–92. doi: 10.1109/MCOM.2018.1700497 AN L T H and TAO P D. The DC (difference of convex functions) programming and DCA revisited with DC models of real world nonconvex optimization problems[J]. Annals of Operations Research, 2005, 133(1): 23–46. doi: 10.1007/s10479-004-5022-1 SRIPERUMBUDUR B K and LANCKRIET G R G. On the convergence of the concave-convex procedure[C]. The 22nd International Conference on Neural Information Processing Systems, Vancouver, British Columbia, Canada, 2009: 1759–1767. FANG Fang, ZHANG Haijun, CHENG Julian, et al. Energy efficiency of resource scheduling for non-orthogonal multiple access (NOMA) wireless network[C]. 2016 IEEE International Conference on Communications, Kuala Lumpur, Malaysia, 2016: 1–5. doi: 10.1109/ICC.2016.7511239. CHEN Qimei, YU Guanding, YIN Rui, et al. Energy-efficient user association and resource allocation for multistream carrier aggregation[J]. IEEE Transactions on Vehicular Technology, 2016, 65(8): 6366–6376. doi: 10.1109/TVT.2015.2472558 BAZARAA M S, SHERALI H D, and SHETTY C M. Nonlinear Programming: Theory and Algorithms[M]. 3rd ed. New York: Wiley, 2013. YE Qiaoyang, RONG Beiyu, CHEN Yudong, et al. User association for load balancing in heterogeneous cellular networks[J]. IEEE Transactions on Wireless Communications, 2013, 12(6): 2706–2716. doi: 10.1109/TWC.2013.040413.120676 KHA H H, TUAN H D, and NGUYEN H H. Fast global optimal power allocation in wireless networks by local D.C. programming[J]. IEEE Transactions on Wireless Communications, 2012, 11(2): 510–515. doi: 10.1109/TWC.2011.120911.110139 -





 下载:
下载:


 下载:
下载:
