Probability Approximation Message Passing Detection Algorithm Based on Early Termination of Iteration
-
摘要: 大规模多输入多输出技术作为第5代通信系统的关键技术,可有效提高频谱利用率。基站端采用消息传递检测(MPD)算法可以实现良好的检测性能。但是由于MPD算法的计算复杂度随调制阶数和用户天线数的增加而增加,而概率近似消息传递检测(PA-MPD)算法可以减少MPD算法的计算复杂度。为了进一步降低PA-MPD算法的复杂度,该文在PA-MPD算法的基础上引入了提前终止迭代策略,提出了一种改进的概率近似消息传递检测算法(IPA-MPD)。首先确定不同用户的符号概率在迭代过程中的收敛速率,然后根据收敛率来判断用户的符号概率是否达到最佳收敛,最后对符号概率到达最佳收敛的用户终止算法迭代。仿真结果表明,在不同单天线用户配置下IPA-MPD算法的计算复杂度可降低为PA-MPD算法的52%~77%,且不损失算法的检测性能。
-
关键词:
- 大规模MIMO /
- 消息传递检测 /
- 概率近似消息传递检测 /
- 提前终止迭代
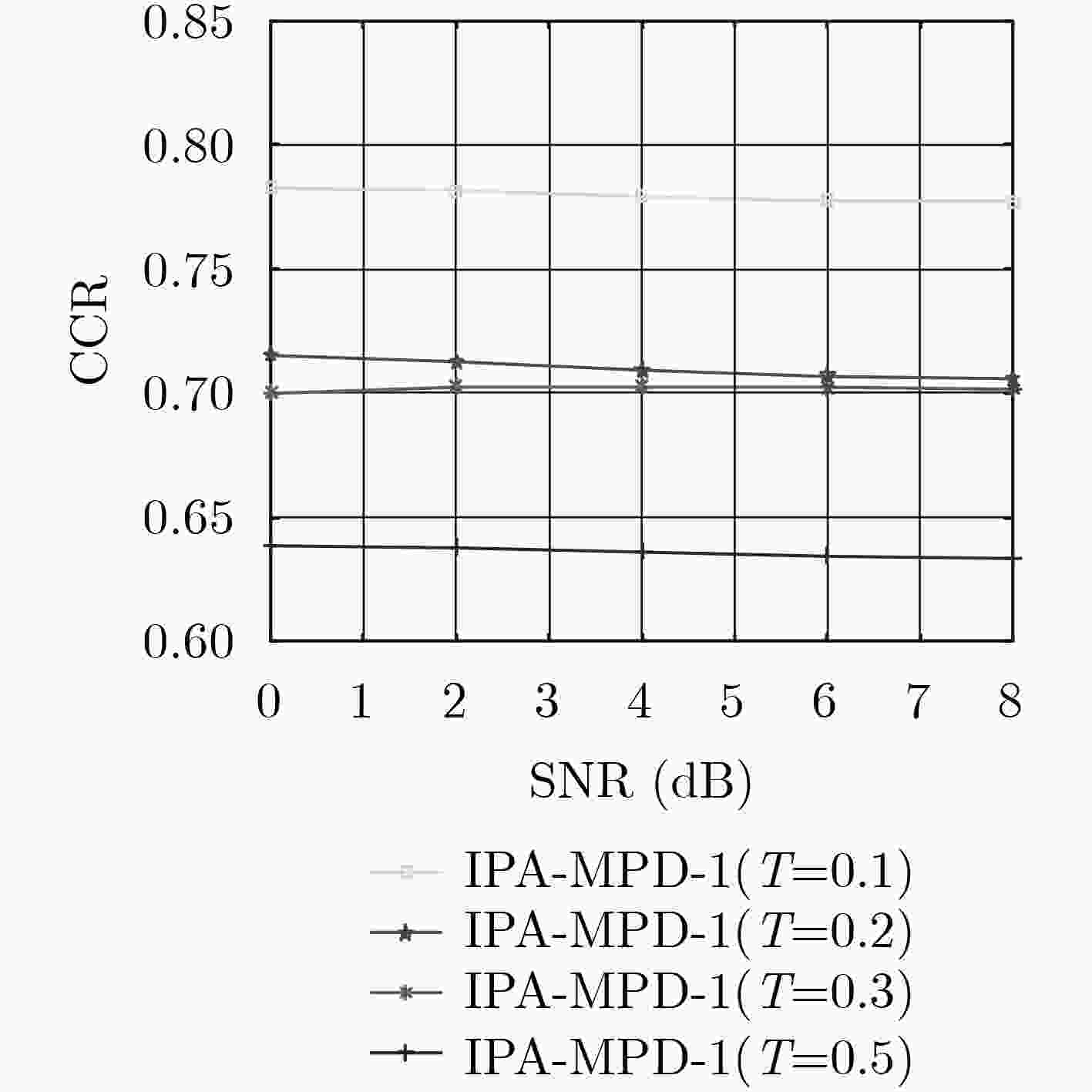
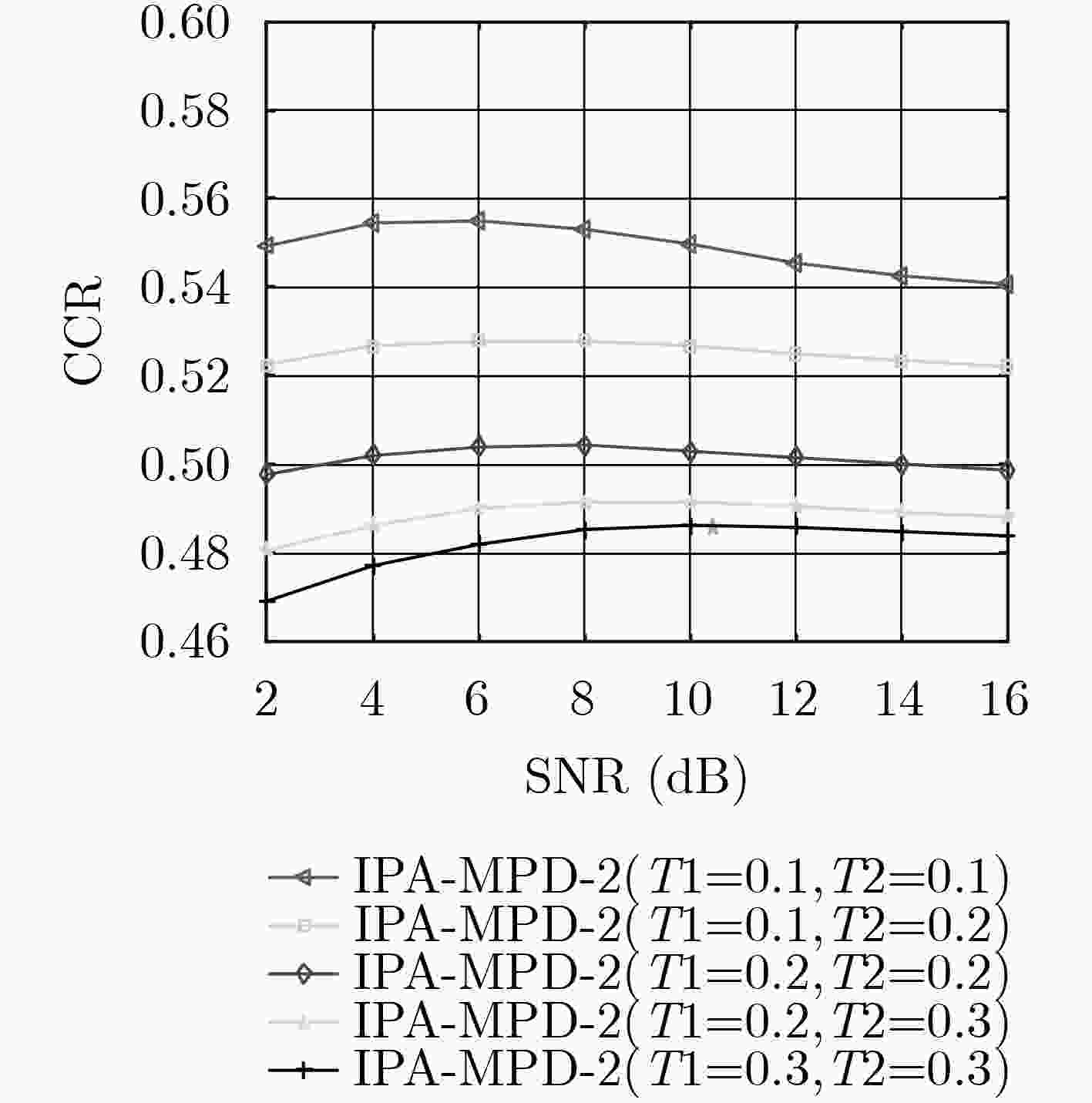
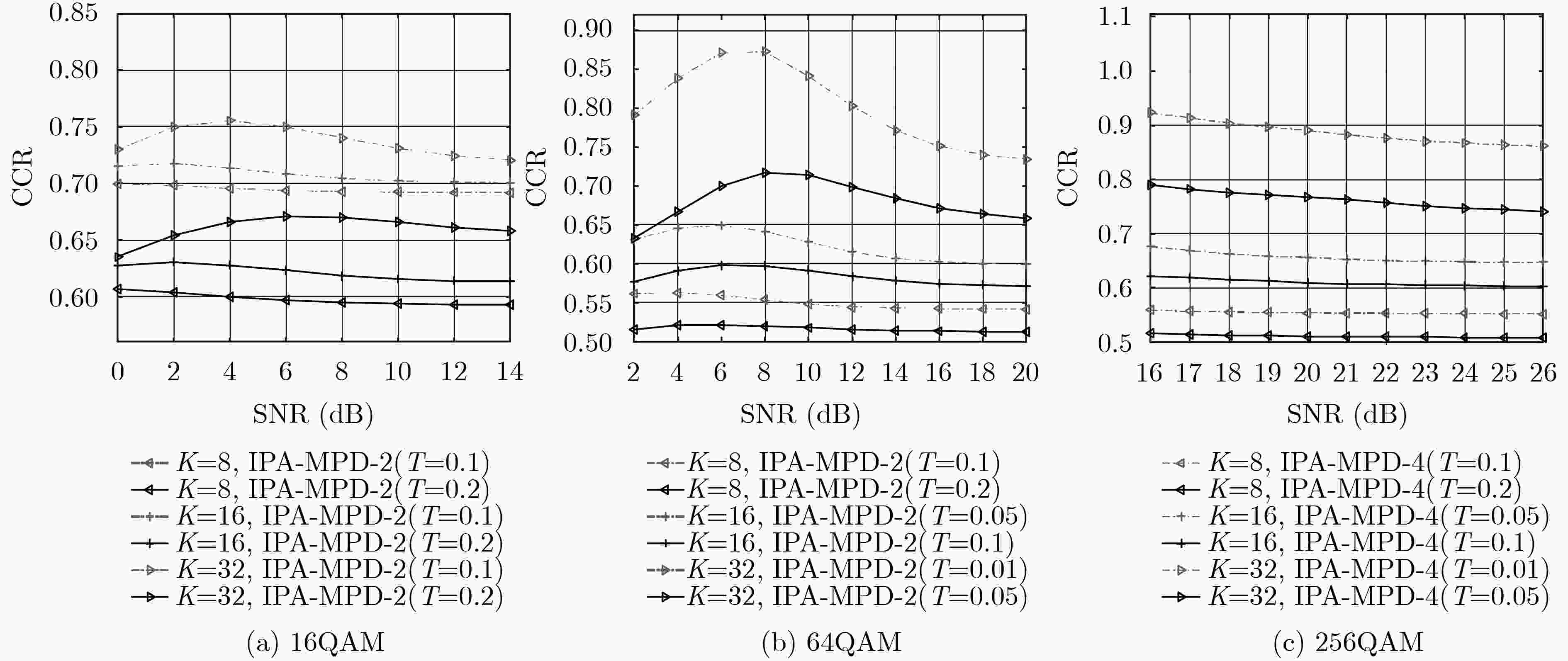
Abstract: As a key technology of the fifth generation communication system, large-scale Multi-Input and Multi-Output(MIMO) technology can effectively improve spectrum utilization. The base station side uses the Message Passing Detection (MPD) algorithm to achieve good detection performance. However, the computational complexity of the MPD algorithm increases with the increase of the modulation order and the number of user antennas, and the Probability Approximation Message Passing Detection (PA-MPD) algorithm can reduce the computational complexity of the MPD algorithm. In order to further reduce the complexity of PA-MPD algorithm, this paper introduces an early termination iteration strategy based on PA-MPD algorithm, and proposes an Improved PA-MPD (IPA-MPD) algorithm. Firstly, the convergence rate of the symbol probability of different users in the iterative process is determined, and then the convergence probability is used to determine whether the user’s symbol probability reaches the best convergence. Finally, the user termination algorithm that the symbol probability reaches the best convergence is iterated. The simulation results show that the computational complexity of the IPA-MPD algorithm can be reduced to 52%~77% of the PA-MPD algorithm under different single-antenna user configurations without loss of the detection performance of the algorithm. -
表 1 IPA-MPD算法
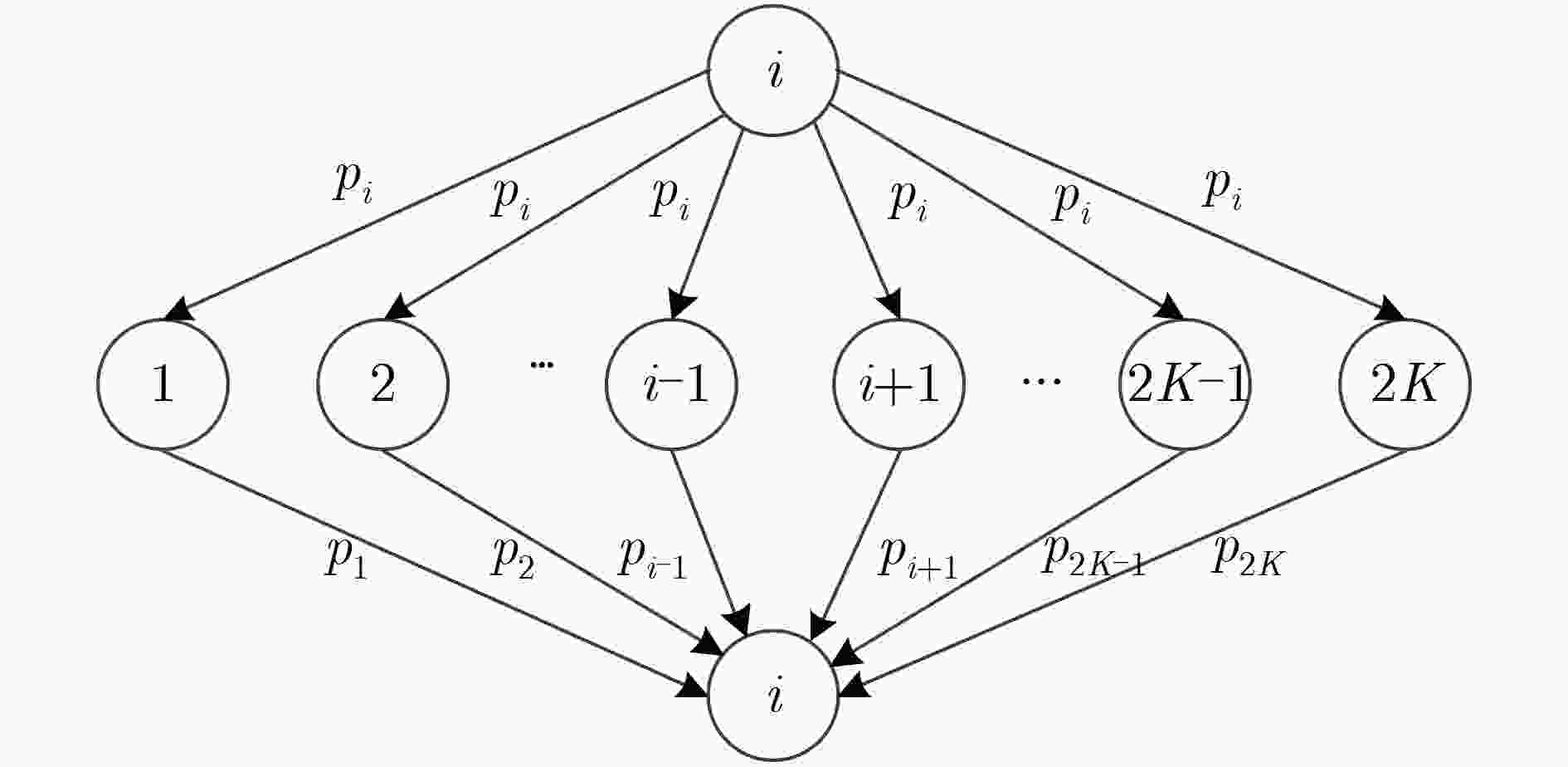
输入:$J,Z,\sigma _v^2,\varDelta ,T$ 输出:L 1: 初始化:${p_i}({s_k}) = \dfrac{1}{ {\sqrt M } },i = 1,2, ··· ,2K,k = 1,2, ··· ,\sqrt M ,$
${R^1}({x_j}) = 1 $2: ${\rm{for} }\;t = 1\;{\rm{do}}$ 3: ${\rm{for} }\;i = 1\;{\rm{to}}\;2K\;{\rm{do}}$
4: $ {{\mu }_{i}}\leftarrow \displaystyle\sum\limits_{j=1,j\ne i}^{2K}{{{J}_{ij}}\displaystyle\sum\limits_{\forall s\in \mathbb{B}}{sp_{j}^{t-1}(s)}} $5: $\sigma _{i}^{2}\leftarrow \displaystyle\sum\limits_{j=1,j\ne i}^{2K}J_{ij}^{2}\left(\displaystyle\sum\limits_{\forall s\in \mathbb{B} }{ { {s}^{2} }p_{j}^{t-1}(s)}-E{ {({ {x}_{j} })}^{2} } \right)+\sigma _{v}^{2}$ 6: $ {{L}_{i}}\leftarrow \dfrac{2{{J}_{ii}}}{\sigma _{i}^{2}}({{z}_{i}}-{{\mu }_{i}}) $ 7: ${ { {\tilde{p} } }_{i} }\leftarrow \dfrac{ { {{\rm{e}}}^{ { {L}_{i} } } }}{1+{ {{\rm{e}}}^{ { {L}_{i} } } }}$ 8: ${p_i} \leftarrow (1 - \varDelta ){ {\tilde p}_i} + \Delta { {\tilde p}_i}$ 9: $ {A_i} \leftarrow {\rm{sort}}({\rm{ }}{p_i}) $ 10: end 11: end 12: ${\rm{for} }\;t = 2\;{\rm{to}}\;{T_{\max } }\;{\rm{do}}$ 13: ${\rm{for} }\;i = 1\;{\rm{to}}\;2K\;{\rm{do}}$ 14: $ {\rm{if}}\;{R^{t - 1}}({x_i}) < T$ 15: 终止迭代 16: else
17: ${\mu _i} \leftarrow \displaystyle\sum\limits_{j = 1,j \ne i}^{2K} { {J_{ij} }\displaystyle\sum\limits_{p_j^{t - 1}(s) \in {A_j}(1,2, ··· ,M)} {sp_j^{t - 1}(s)} }$18: $\sigma _i^2 \leftarrow \displaystyle\sum\limits_{j = 1,j \ne i}^{2K} {J_{ij}^2}\left (\displaystyle\sum\limits_{p_j^{t - 1}(s) \in {A_j}(1,2, ··· ,M)} {sp_j^{t - 1}(s)} - \right.$
$ \Biggl.{19} E{({x_j})^2} \Bigggr){19}+ \sigma _v^2 $19: $ {L_i} \leftarrow \dfrac{{2{J_{ii}}}}{{\sigma _i^2}}({z_i} - {\mu _i}) $ 20: ${ {\tilde p}_i} \leftarrow \dfrac{ { {{\rm{e}}^{ {L_i} } } }}{ {1 + {{\rm{e}}^{ {L_i} } } }}$ 21: ${p_i} \leftarrow (1 - \varDelta ){ {\tilde p}_i} + \Delta { {\tilde p}_i}$ 22: $ {A_i} \leftarrow {\rm{sort}}({\rm{ }}{p_i}) $ 23: $ {R^t}({x_i}) \leftarrow \displaystyle\sum\limits_{k = 1}^{\sqrt M } {|p_{{x_i}}^t({s_k}) - p_{{x_i}}^{t - 1}({s_k})|} $ 24: end 21: end 22: end 表 2 M-QAM调制下PA-MPD[10]算法和IPA-MPD算法的实数域乘法和加法次数
算法名称 加法 乘法 PA-MPD-n $\begin{array}{l}((2n + 1)(2K - 1) - 2)2K(t - 1)\\ + ((2\sqrt M {\rm{ + 1}})2K - 1 - {\rm{1}}){\rm{2}}K\end{array}$ $\begin{array}{l} (2n + 1)(2K - 1)2K(t - 1) \\ + (2\sqrt M + 1)(2K - 1)2K \\ \end{array} $ IPA-MPD-n $\begin{array}{l}((2n + 1)(2K - 1) - 2)2K({t_{{\rm{ave}}}} - 1)\\ + ((2\sqrt M {\rm{ + 1}})2K - 1 - {\rm{1}}){\rm{2}}K\end{array}$ $\begin{array}{l}(2n + 1)(2K - 1)2K({t_{{\rm{ave}}}} - 1)\\ + ((2\sqrt M {\rm{ + 1}})2K - 1 - {\rm{1}}){\rm{2}}K\end{array}$ -
HE Hengtao, WEN Chaokai, JIN Shi, et al. A model-driven deep learning network for MIMO detection[C]. 2018 IEEE Global Conference on Signal and Information Processing, Anaheim, USA, 2018: 584–588. DUANGSUWAN S and JAMJAREEGULGARN P. Detection of data symbol in a massive MIMO systems for 5G wireless communication[C]. 2017 International Electrical Engineering Congress, Pattaya, Thailand, 2017: 1–4. YANG Shaoshi and HANZO L. Fifty years of MIMO detection: The road to large-scale MIMOs[J]. IEEE Communications Surveys & Tutorials, 2015, 17(4): 1941–1988. doi: 10.1109/COMST.2015.2475242 FREY B J. Graphical Models for Machine Learning and Digital Communication[M]. Cambridge: The MIT Press, 1998: 25–34. SOM P, DATTA T, CHOCKALINGAM A, et al. Improved large-MIMO detection based on damped belief propagation[C]. 2010 IEEE Information Theory Workshop on Information Theory, Cairo, Egypt, 2010: 1–5. USAMI T, NISHIMURA T, OHGANE T, et al. BP-based detection of spatially multiplexed 16-QAM signals in a fully massive MIMO system[C]. 2016 International Conference on Computing, Networking and Communications, Kauai, USA, 2016: 166–170. SOM P, DATTA T, SRINIDHI N, et al. Low-complexity detection in large-dimension MIMO-ISI channels using graphical models[J]. IEEE Journal of Selected Topics in Signal Processing, 2011, 5(8): 1497–1511. doi: 10.1109/JSTSP.2011.2166950 WU Sheng, KUANG Linling, NI Zuyao, et al. Low-complexity iterative detection for large-scale multiuser MIMO-OFDM systems using approximate message passing[J]. IEEE Journal of Selected Topics in Signal Processing, 2014, 8(5): 902–915. doi: 10.1109/JSTSP.2014.2313766 NARASIMHAN T L and CHOCKALINGAM A. Channel hardening-exploiting message passing (CHEMP) receiver in large-scale MIMO systems[J]. IEEE Journal of Selected Topics in Signal Processing, 2014, 8(5): 847–860. doi: 10.1109/JSTSP.2014.2314213 ZHU Haochuan, LIN Jun, and WANG Zhongfeng. Reduced complexity message passing detection algorithm in large-scale MIMO systems[C]. The 9th International Conference on Wireless Communications and Signal Processing, Nanjing, China, 2017: 1–5. ZENG Jing, LIN Jun, and WANG Zhongfeng. Low complexity message passing detection algorithm for large-scale MIMO systems[J]. IEEE Wireless Communications Letters, 2018, 7(5): 708–711. doi: 10.1109/LWC.2018.2813386 TAN Xiaosi, ZHONG Zhiwei, ZHANG Zaichen, et al. Low-complexity message passing MIMO detection algorithm with deep neural network[C]. Proceedings of 2018 IEEE Global Conference on Signal and Information Processing, Anaheim, USA, 2018: 559–563. GOLDBERGER J and LESHEM A. MIMO detection for high-order QAM based on a Gaussian tree approximation[J]. IEEE Transactions on Information Theory, 2011, 57(8): 4973–4982. doi: 10.1109/TIT.2011.2159037 GU Lixin, WANG Wenjin, ZHONG Wen, et al. Message-passing detector for uplink massive MIMO systems based on energy spread transform[C]. The 27th IEEE Annual International Symposium on Personal, Indoor, and Mobile Radio Communications, Valencia, Spain, 2016: 1–6. JIA Min, WANG Linfang, GUO Qing, et al. A low complexity detection algorithm for fixed up-link SCMA System in mission critical scenario[J]. IEEE Internet of Things Journal, 2018, 5(5): 3289–3297. doi: 10.1109/JIOT.2017.2696028 LIU Lei, YUEN C, GANG Yongliang, et al. Convergence analysis and assurance for Gaussian message passing iterative detector in massive MU-MIMO systems[J]. IEEE Transactions on Wireless Communications, 2016, 15(9): 6487–6501. doi: 10.1109/TWC.2016.2585481 YANG Chao, XU Weihong, ZHANG Zaichen, et al. A channel-blind detection for SCMA based on image processing techniques[C]. 2018 IEEE International Symposium on Circuits and Systems, Florence, Italy, 2018: 1–5. -





 下载:
下载:


 下载:
下载:
