|
刘松, 庞育才. 基于扩展ESPRIT的随机阵列高效DOA估计算法[J]. 电子与信息学报, 2019, 41(6): 1324–1329. doi: 10.11999/JEIT180672LIU Song and PANG Yucai. Efficient augmented ESPRIT-based direction-of-arrival estimation algorithm for random arrays[J]. Journal of Electronics &Information Technology, 2019, 41(6): 1324–1329. doi: 10.11999/JEIT180672
|
|
杨康, 文方青, 黄冬梅, 等. 基于实值三线性分解的互耦条件下双基地MIMO雷达角度估计算法[J]. 系统工程与电子技术, 2018, 40(2): 314–321. doi: 10.3969/j.issn.1001-506X.2018.02.12YANG Kang, WEN Fangqing, HUANG Dongmei, et al. Real-value-based trilinear decomposition-based direction estimation algorithm for bistatic MIMO radar in the presence of mutual coupling[J]. Systems Engineering and Electronics, 2018, 40(2): 314–321. doi: 10.3969/j.issn.1001-506X.2018.02.12
|
|
赵洋, 李新波, 石要武. 声矢量阵列波达方向估计的四元数空间稀疏分解[J]. 光学精密工程, 2018, 26(3): 715–722. doi: 10.3788/OPE.20182603.0715ZHAO Yang, LI Xinbo, and SHI Yaowu. Quaternion sparse decomposition algorithm for DOA estimation with acoustic vector sensor array[J]. Optics and Precision Engineering, 2018, 26(3): 715–722. doi: 10.3788/OPE.20182603.0715
|
|
史云飞, 郝永生, 刘德亮, 等. RSS协助的Ray-tracing室内定位算法[J]. 信号处理, 2018, 34(10): 1259–1266. doi: 10.16798/j.issn.1003-0530.2018.10.015SHI Yunfei, HAO Yongsheng, LIU Deliang, et al. RSS-assisted Ray-tracing indoor positioning algorithm[J]. Journal of Signal Processing, 2018, 34(10): 1259–1266. doi: 10.16798/j.issn.1003-0530.2018.10.015
|
|
CHEN Y H and LIAN Y T. 2-D multitarget angle tracking algorithm using sensor array[J]. IEE Proceedings – Radar, Sonar and Navigation, 1995, 142(4): 158–161. doi: 10.1049/ip-rsn:19951984
|
|
陈建, 王树勋, 魏小丽. 一种基于L型阵列的二维波达方向估计的新方法[J]. 吉林大学学报: 工学版, 2006, 36(4): 590–593.CHEN Jian, WANG Shuxun, and WEI Xiaoli. New method for estimating two-dimensional direction of arrival based on L-shape array[J]. Journal of Jilin University:Engineering and Technology Edition, 2006, 36(4): 590–593.
|
|
景小荣, 刘雪峰. L型阵列的二维DOA估计方法[J]. 重庆邮电大学学报: 自然科学版, 2016, 28(1): 24–29. doi: 10.3979/j.issn.1673-825X.2016.01.004JING Xiaorong and LIU Xuefeng. Method of two-dimensional DOA estimation for L-shaped array[J]. Journal of Chongqing University of Posts and Telecommunications:Natural Science Edition, 2016, 28(1): 24–29. doi: 10.3979/j.issn.1673-825X.2016.01.004
|
|
ZHANG Xiaofei, LI Jianfeng, and XU Lingyun. Novel two-dimensional DOA estimation with L-shaped array[J]. EURASIP Journal on Advances in Signal Processing, 2011, 2011(1): 50. doi: 10.1186/1687-6180-2011-50
|
|
杨艳飞, 高健, 张兴敢. 一种基于L型阵列的改进的二维DOA估计方法[J]. 南京大学学报: 自然科学, 2016, 52(5): 953–959. doi: 10.13232/j.cnki.jnju.2016.05.023YANG Yanfei, GAO Jian, and ZHANG Xinggan. An improved method for estimating two-dimensional DOA based on L-shape array[J]. Journal of Nanjing University:Natural Sciences, 2016, 52(5): 953–959. doi: 10.13232/j.cnki.jnju.2016.05.023
|
|
FRIEDLANDER B and WEISS A J. Direction finding using spatial smoothing with interpolated arrays[J]. IEEE Transactions on Aerospace and Electronic Systems, 1992, 28(2): 574–587. doi: 10.1109/7.144583
|
|
GU Jianfeng, WEI Ping, and TAI Hengming. 2-D direction-of-arrival estimation of coherent signals using cross-correlation matrix[J]. Signal Processing, 2008, 88(1): 75–85. doi: 10.1016/j.sigpro.2007.07.013
|
|
史清响, 马秀荣, 谢玉凤, 等. 基于相关矢量法L型阵列相干信号DOA估计[J]. 科学技术与工程, 2015, 15(8): 194–198. doi: 10.3969/j.issn.1671-1815.2015.08.037SHI Qingxiang, MA Xiurong, XIE Yufeng, et al. DOA estimation of coherent signals based on correlation vector method with L-shaped array[J]. Science Technology and Engineering, 2015, 15(8): 194–198. doi: 10.3969/j.issn.1671-1815.2015.08.037
|
|
刁鸣, 安春莲. 独立信号与相干信号并存的二维DOA估计新方法[J]. 西安电子科技大学学报: 自然科学版, 2013, 40(5): 66–71, 98. doi: 10.3969/j.issn.1001-2400.2013.05.011DIAO Ming and AN Chunlian. 2-D DOA estimation of coexisting uncorrelated and coherent signals[J]. Journal of Xidian University, 2013, 40(5): 66–71, 98. doi: 10.3969/j.issn.1001-2400.2013.05.011
|
|
QIAN Cheng, HUANG Lei, CAO Mingyang, et al. PUMA: An improved realization of MODE for DOA estimation[J]. IEEE Transactions on Aerospace and Electronic Systems, 2017, 53(5): 2128–2139. doi: 10.1109/TAES.2017.2683598
|
|
LIU Z M, LU Z Y, HUANG Z T, et al. Improved Gerschgorin disk estimator for source enumeration with robustness against spatially non-uniform noise[J]. IET Radar, Sonar & Navigation, 2011, 5(9): 952–957. doi: 10.1049/iet-rsn.2011.0188
|
|
安春莲. 独立信号与相干信号并存的测向算法研究[D]. [博士论文], 哈尔滨工程大学, 2013.AN Chunlian. Research on direction finding for coexisted uncorrelated and coherent sources[D]. [Ph. D. dissertation], Harbin Engineering University, 2013.
|
|
WEI Yinsheng and GUO Xiaojiang. Pair-matching method by signal covariance matrices for 2D-DOA estimation[J]. IEEE Antennas and Wireless Propagation Letters, 2014, 13: 1199–1202. doi: 10.1109/LAWP.2014.2331076
|





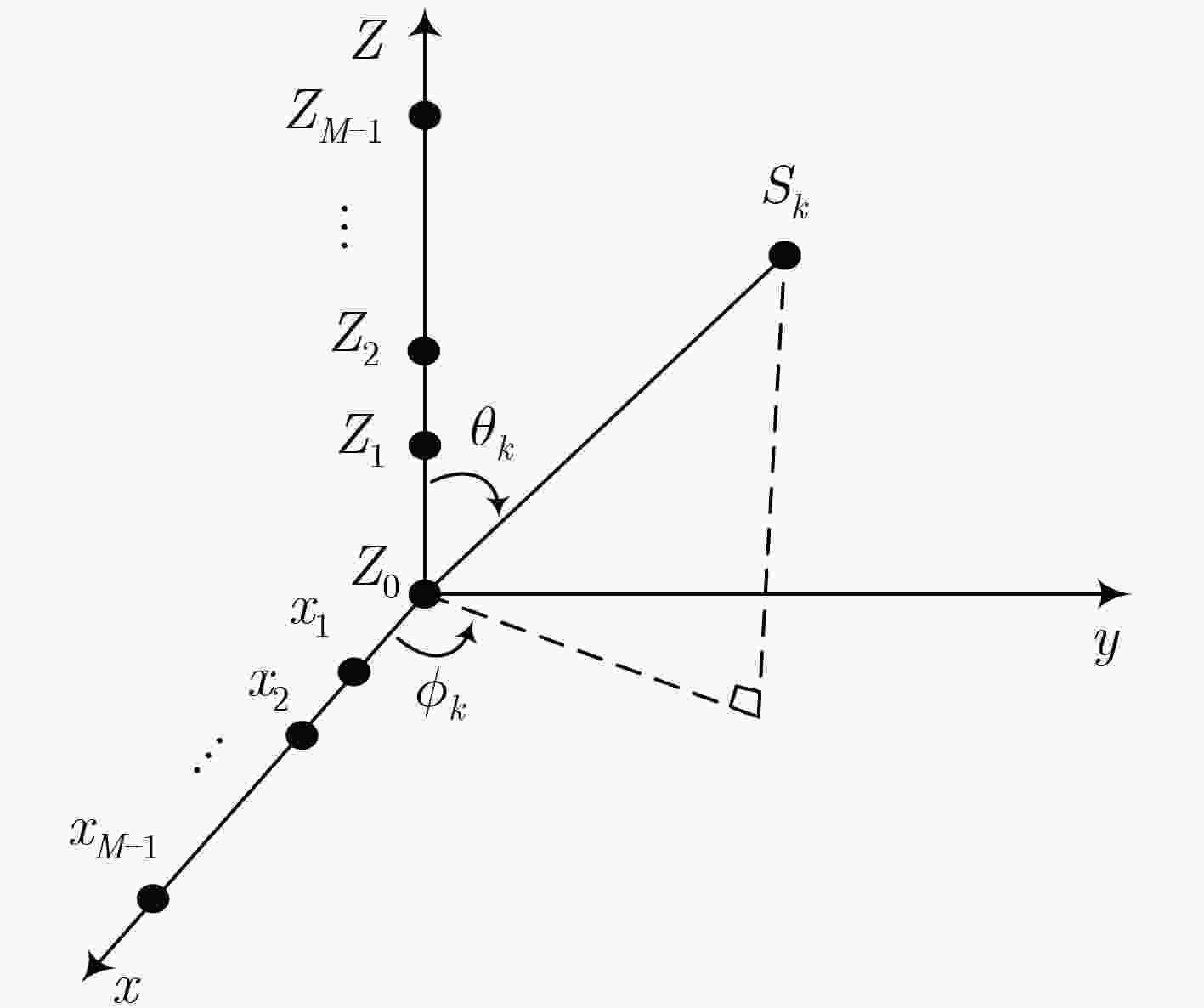
 下载:
下载:
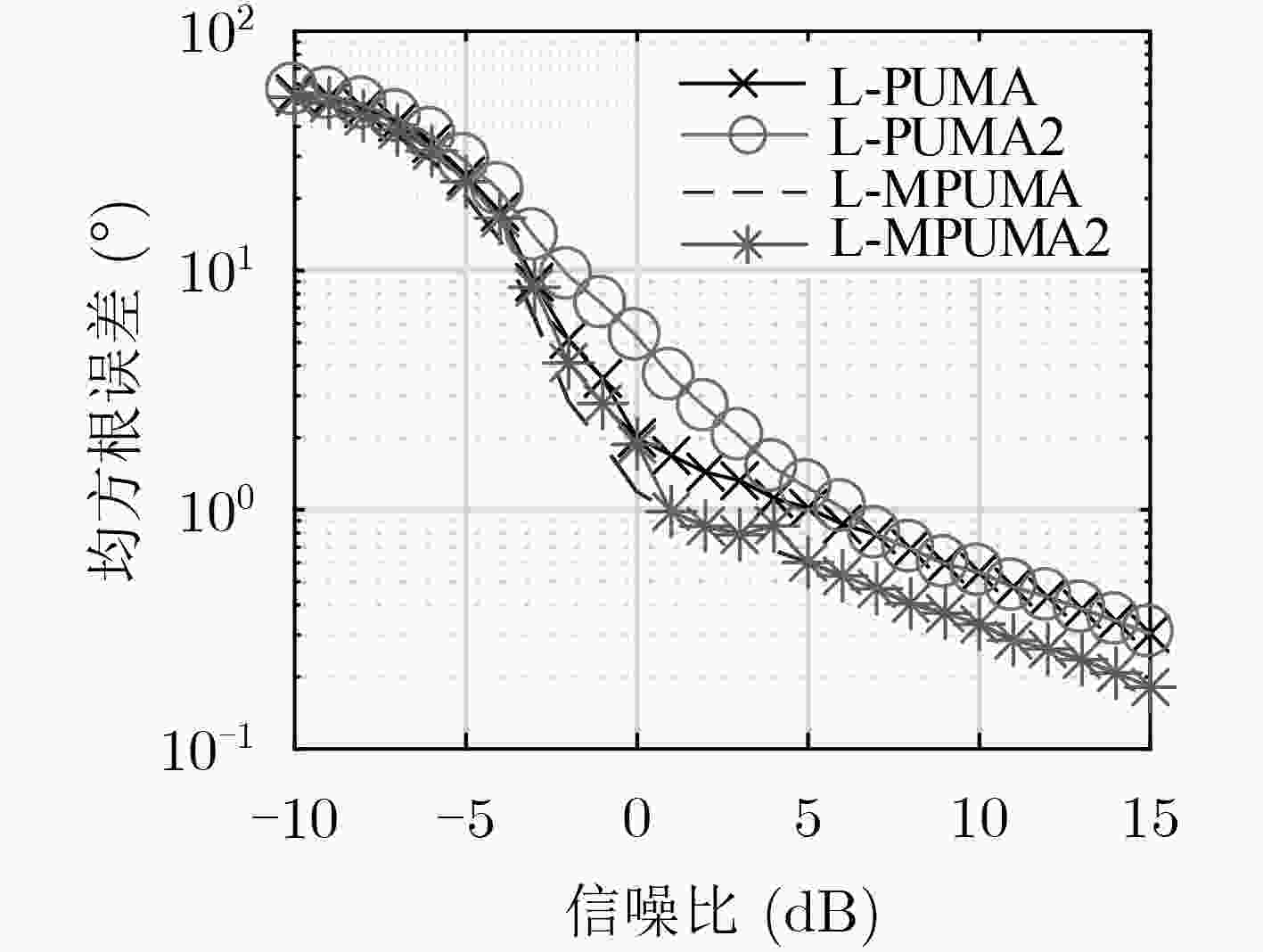
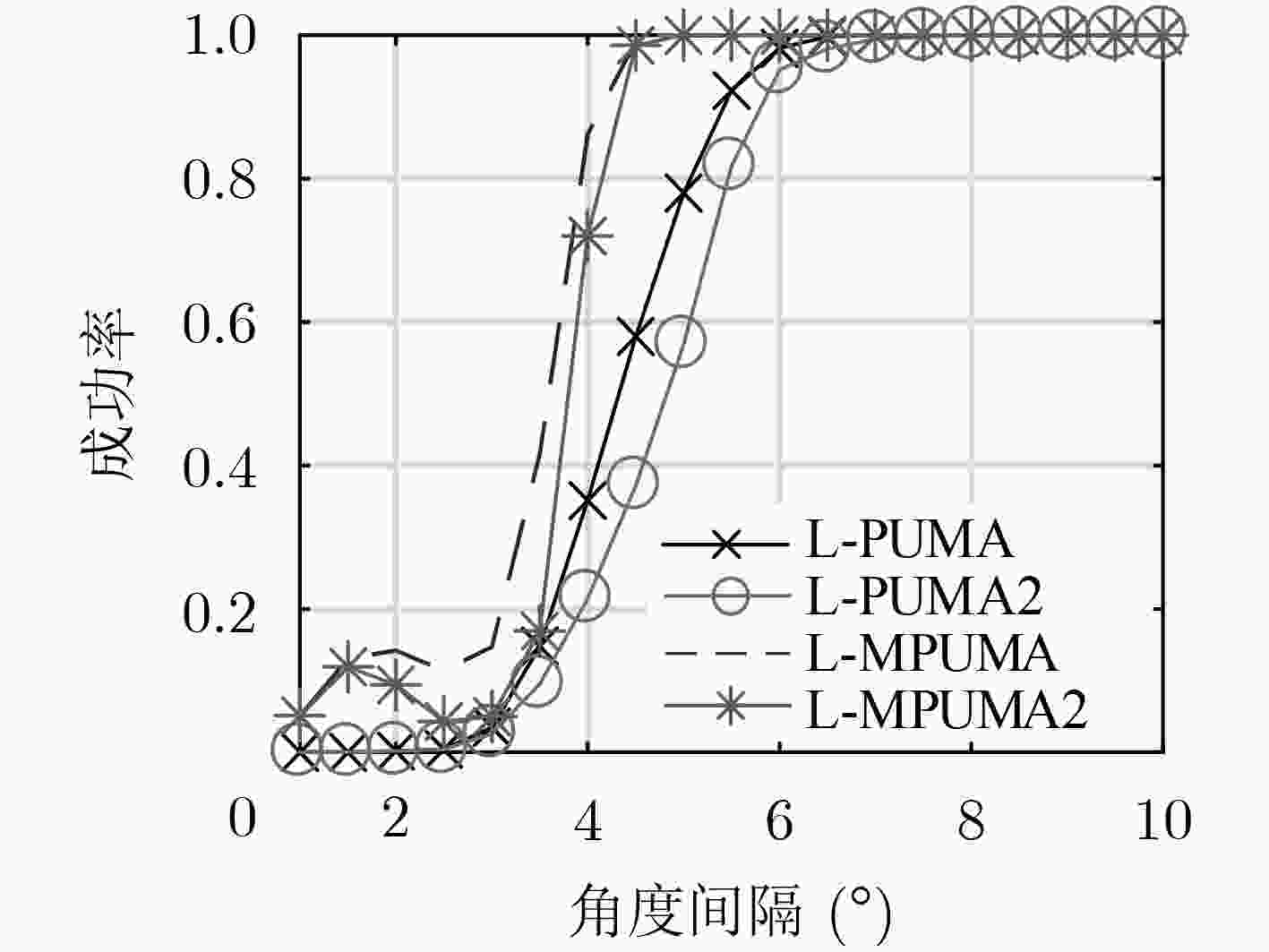
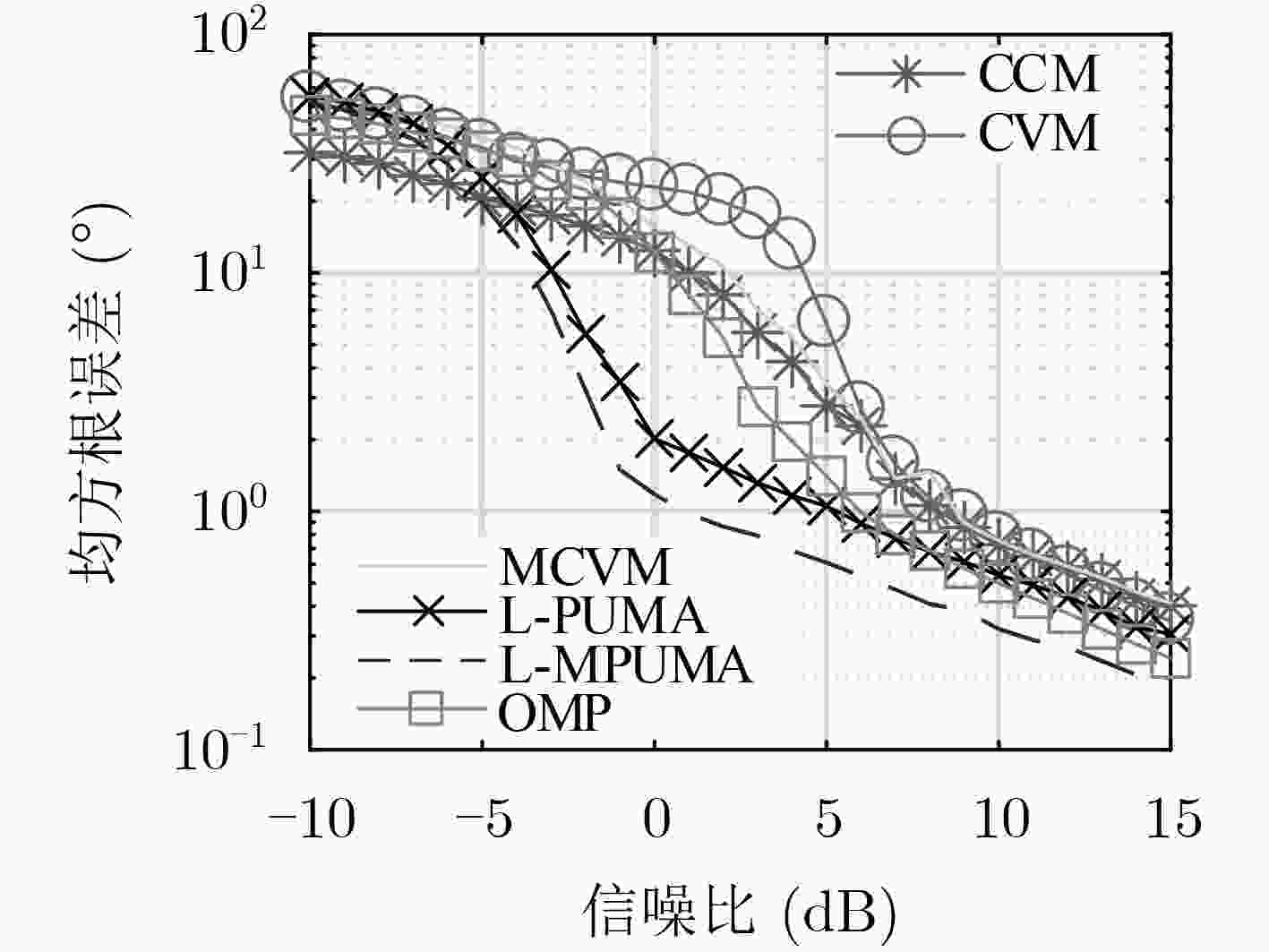
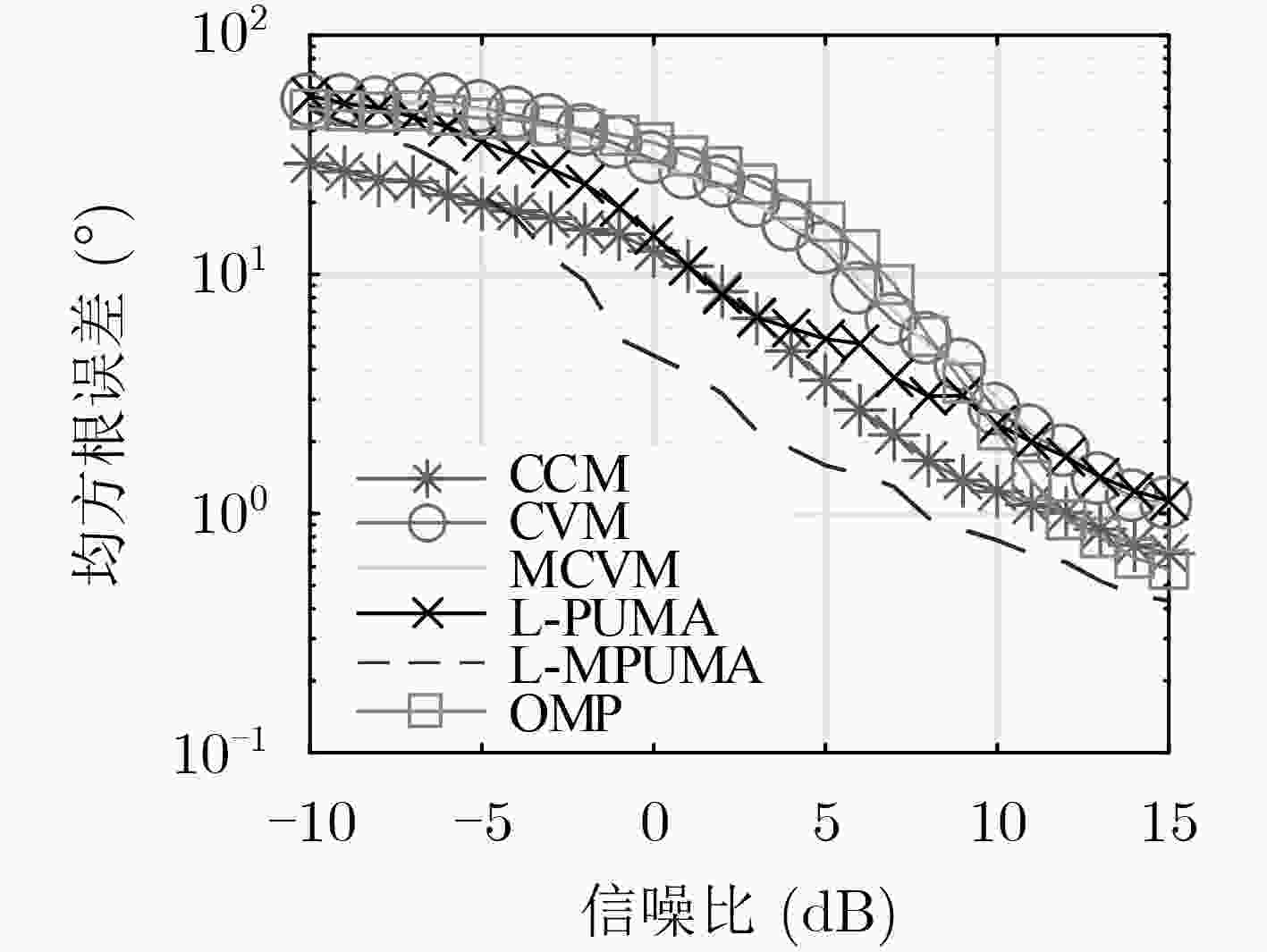
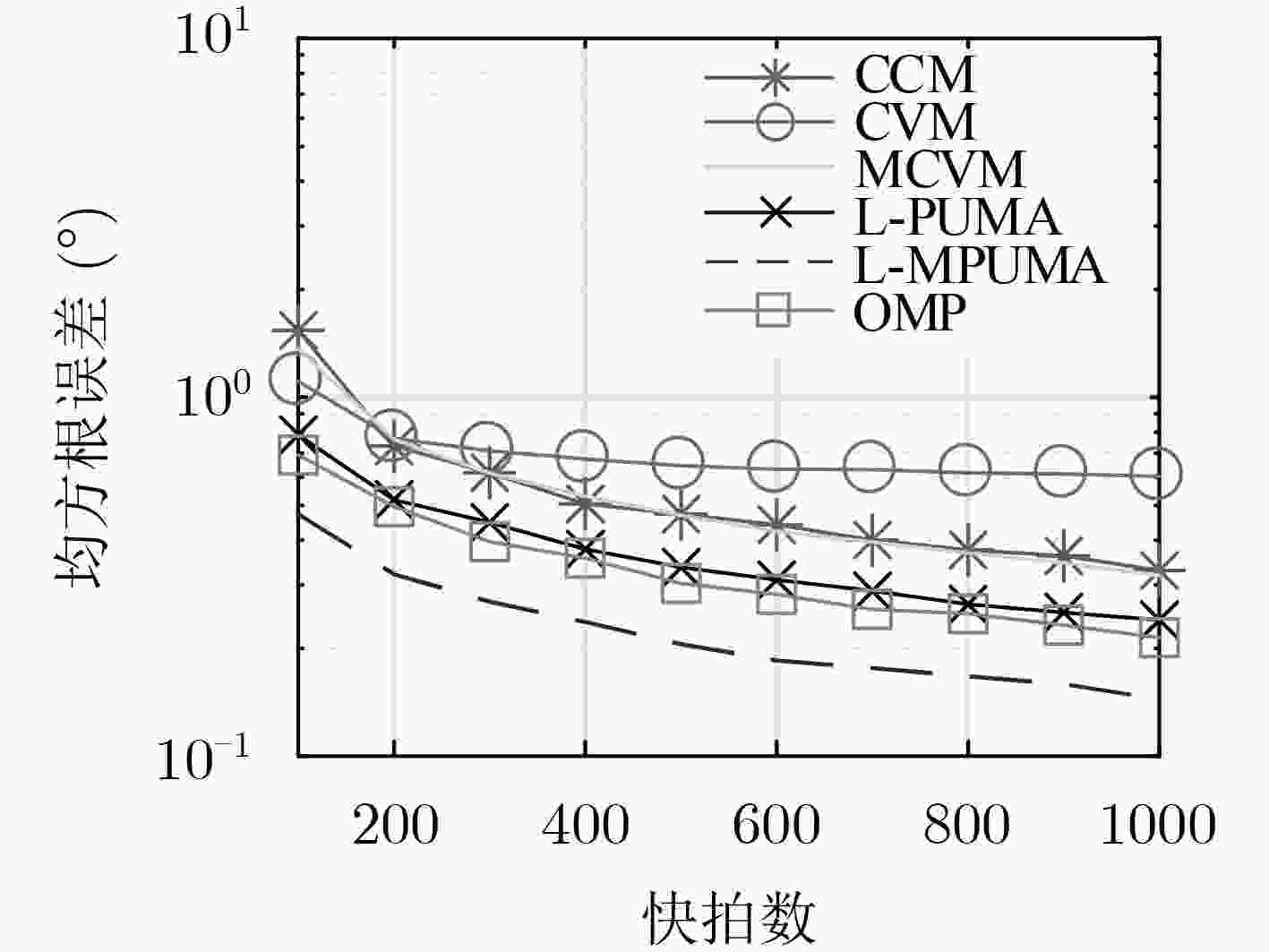
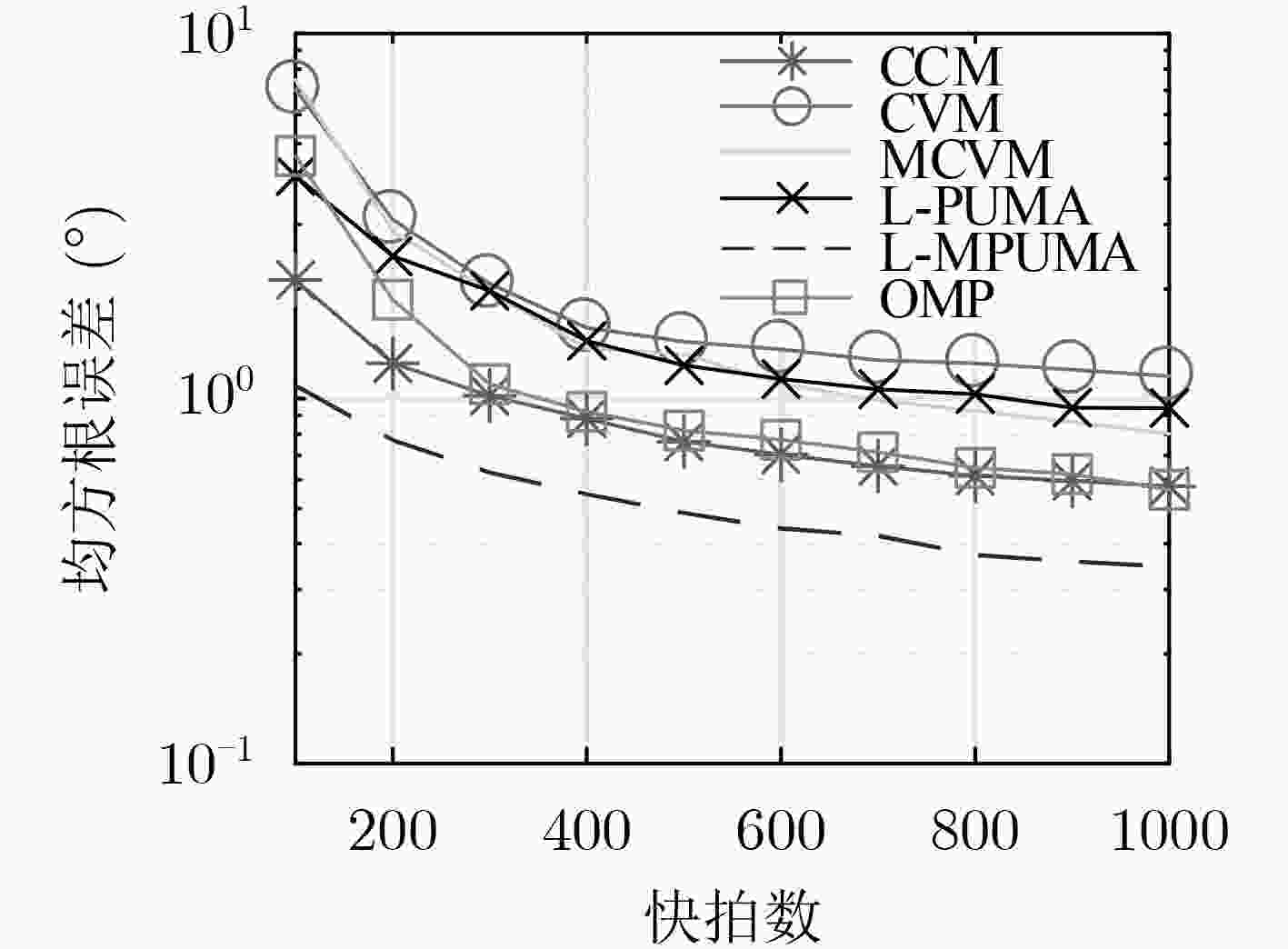
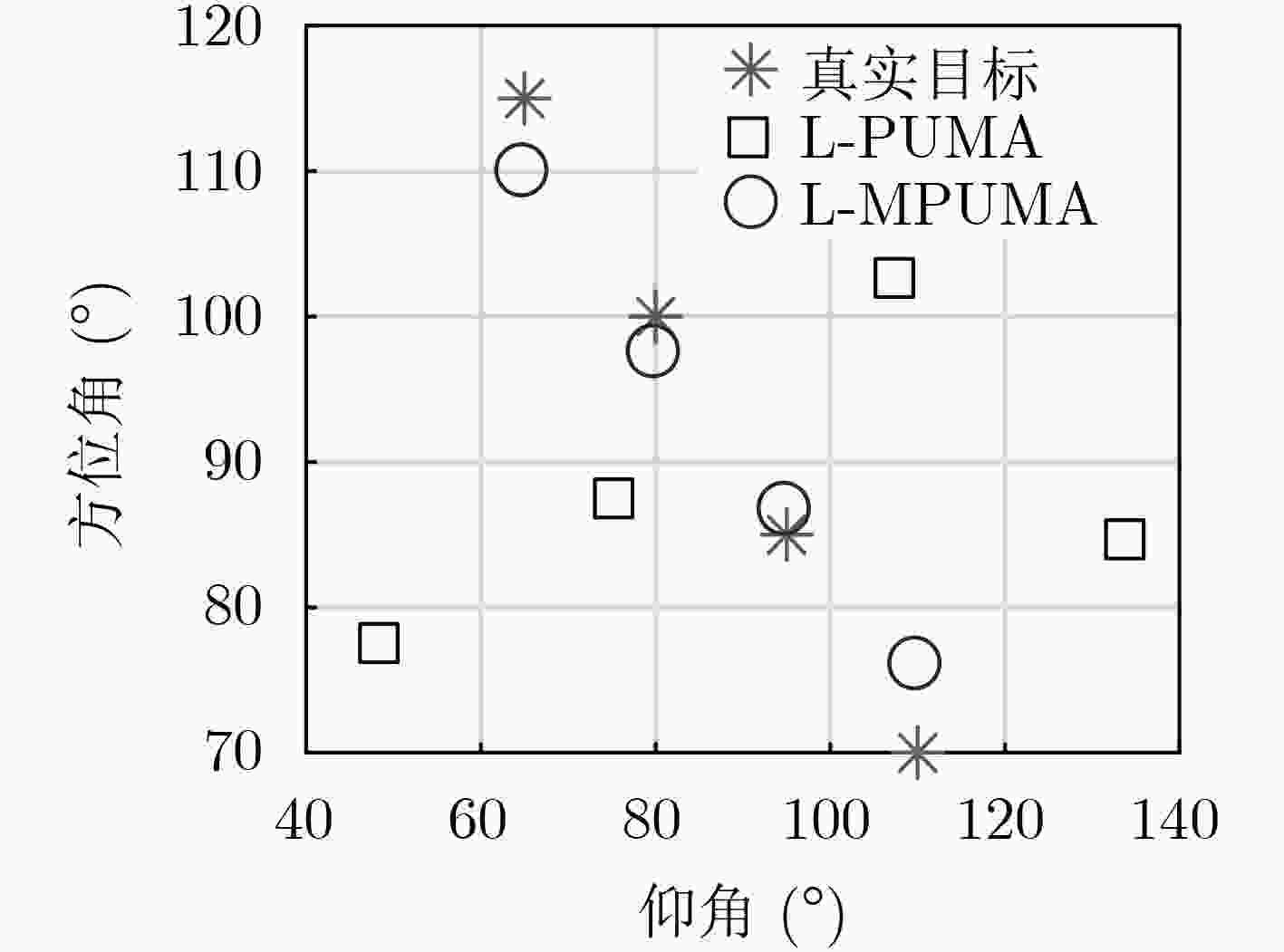


 下载:
下载:
