A TDOA-FDOA Passive Positioning Algorithm Based on the Semi-Definite Relaxation Technique
-
摘要:
在运动目标的无源定位场景下,闭式算法在低噪声情况下可以到达克拉美罗下界(CRLB),但是这些算法往往不能适应较大的测量噪声环境。针对目前闭式算法适应大噪声能力较差这一问题,该文联合到达时间差(TDOA)以及到达频率差(FDOA),提出一种基于半定松弛(SDR)技术的无源定位算法。该算法首先构建传统闭式解的伪线性方程,其次利用随机鲁棒最小二乘(SRLS)的思想以及目标参数与额外变量之间的非线性关系,将无源定位问题转化为了具有2次等式约束的最小二乘问题;随后,将半定松弛技术应用到这一问题上,约束最小二乘问题松弛为半定规划(SDP)问题,最后,借助优化工具箱可以有效地对目标参数进行求解。该文所提出的算法不需要初始值先验条件,仿真实验表明了所提算法的有效性。
Abstract:In the passive location of moving target, the closed-form solution can reach Cramér-Rao Lower Bound (CRLB) under the low noise level, but these algorithms often can not adapt to the large measurement noise condition. For this problem, this paper proposes a passive positioning algorithm based on the Semi-Definite Relaxation (SDR) using Time Difference Of Arrival (TDOA) and Frequency Difference Of Arrival (FDOA). Firstly, this method constructs the pseudo-linear equation of the typical closed-form solution. Secondly, the idea of Stochastic Robust Least Squares (SRLS) and the nonlinear relationship between the target parameters and the additional variables are used to transform the localization problem into the least squares problem with quadratic equality. Using Semi-Definite Programming (SDP) technique, constrained least squares problem is then converted into the SDP problem, which is finally solved by the optimization toolbox. The proposed method does not require an initial priori information and simulations show the effectiveness of the proposed method.
-
表 1 观测站的位置与速度
序号 位置(m) 速度(m/s) 1 300 100 150 30 –20 20 2 400 150 100 –30 10 20 3 300 500 200 10 –20 10 4 350 200 100 10 20 30 5 –100 –100 –100 –20 20 20 -
王鼎, 胡涛. 无源定位技术-二次等式约束最小二乘估计理论与方法[M]. 北京: 电子工业出版社, 2018: 3–9.WANG Ding and HU Tao. Least-Squares Estimation Theory and Method in Passive Location with Quadratic Equality Constraints[M]. Beijing: Publishing House of Electronics Industry, 2018: 3–9. 朱国辉, 冯大政, 聂卫科. 传感器位置误差情况下基于多维标度分析的时差定位算法[J]. 电子学报, 2016, 44(1): 21–26. doi: 10.3969/j.issn.0372-2112.2016.01.004ZHU Guohui, FENG Dazheng, and NIE Weike. Multidimensional scaling based TDOA localization algorithm with sensor location errors[J]. Acta Electronica Sinica, 2016, 44(1): 21–26. doi: 10.3969/j.issn.0372-2112.2016.01.004 WANG Yue and HO K C. An asymptotically efficient estimator in closed-form for 3-D AOA localization using a sensor network[J]. IEEE Transactions on Wireless Communications, 2015, 14(12): 6524–6535. doi: 10.1109/twc.2015.2456057 赵勇胜, 赵拥军, 赵闯. 基于双基地距离的多站多外辐射源无源定位算法[J]. 电子学报, 2018, 46(12): 2840–2847. doi: 10.3969/j.issn.0372-2112.2018.12.004ZHAO Yongsheng, ZHAO Yongjun, and ZHAO Chuang. Multi-transmitter multi-receiver passive location using bistatic range measurements[J]. Acta Electronica Sinica, 2018, 46(12): 2840–2847. doi: 10.3969/j.issn.0372-2112.2018.12.004 周龙健, 罗景青, 孔辉. 基于虚拟时差的运动阵列空间无源定位算法[J]. 电子与信息学报, 2017, 39(7): 1759–1763. doi: 10.11999/JEIT160860ZHOU Longjian, LUO Jingqing, and KONG Hui. A passive location algorithm based on the virtual TDOAs of moving array[J]. Journal of Electronics &Information Technology, 2017, 39(7): 1759–1763. doi: 10.11999/JEIT160860 TAHAT A, KADDOUM G, YOUSEFI S, et al. A look at the recent wireless positioning techniques with a focus on algorithms for moving receivers[J]. IEEE Access, 2017, 4: 6652–6680. doi: 10.1109/ACCESS.2016.2606486 INDELMAN V, GURFIL P, RIVLIN E, et al. Real-time vision-aided localization and navigation based on three -view geometry[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(3): 2239–2259. doi: 10.1109/TAES.2012.6237590 DEMPSTER A G and CETIN E. Interference localization for satellite navigation systems[J]. Proceedings of the IEEE, 2016, 104(6): 1318–1326. doi: 10.1109/jproc.2016.2530814 FOY W H. Position-location solutions by taylor-series estimation[J]. IEEE Transactions on Aerospace and Electronic Systems, 1976, AES-12(2): 187–194. doi: 10.1109/TAES.1976.308294 HO K C and XU Wenwei. An accurate algebraic solution for moving source location using TDOA and FDOA measurements[J]. IEEE Transactions on Signal Processing, 2004, 52(9): 2453–2463. doi: 10.1109/tsp.2004.831921 KAY S M. Fundamentals of Statistical Signal Processing Volume I: Estimation Theory[M]. Upper Saddle River: Prentice Hall, 1993: 23–45. HO K C, LU Xiaoning, and KOVAVISARUCH L. Source localization using TDOA and FDOA measurements in the presence of receiver location errors: Analysis and solution[J]. IEEE Transactions on Signal Processing, 2007, 55(2): 684–696. doi: 10.1109/tsp.2006.885744 SUM Ming and HO K C. An asymptotically efficient estimator for TDOA and FDOA positioning of multiple disjoint sources in the presence of sensor location uncertainties[J]. IEEE Transactions on Signal Processing, 2011, 59(7): 3434–3440. doi: 10.1109/TSP.2011.2131135 WEI Hewen, PENG Rong, WAN Qun, et al. Multidimensional scaling analysis for passive moving target localization with TDOA and FDOA measurements[J]. IEEE Transactions on Signal Processing, 2010, 58(3): 1677–1688. doi: 10.1109/TSP.2009.2037666 刘洋, 杨乐, 郭福成, 等. 基于定位误差修正的运动目标TDOA/FDOA无源定位方法[J]. 航空学报, 2015, 36(5): 1617–1626. doi: 10.7527/S1000-6893.2015.0010LIU Yang, YANG Le, GUO Fucheng, et al. Moving targets TDOA/FDOA passive localization algorithm based on localization error refinement[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(5): 1617–1626. doi: 10.7527/S1000-6893.2015.0010 NOROOZI A, OVEIS A H, HOSSEINI S M R, et al. Improved algebraic solution for source localization from TDOA and FDOA measurements[J]. IEEE Wireless Communications Letters, 2018, 7(3): 352–355. doi: 10.1109/LWC.2017.2777995 周恭谦, 杨露菁, 刘忠. 改进的非完全约束加权最小二乘TDOA/FDOA无源定位方法[J]. 系统工程与电子技术, 2018, 40(8): 1686–1692. doi: 10.3969/j.issn.1001-506X.2018.08.03ZHOU Gongqian, YANG Luqing, and LIU Zhong. Improved incomplete constrained weighted least squares TDOA/FDOA passive location method[J]. Systems Engineering and Electronics, 2018, 40(8): 1686–1692. doi: 10.3969/j.issn.1001-506X.2018.08.03 WANG Gang, LI Youming, and ANSARI N. A semidefinite relaxation method for source localization using TDOA and FDOA measurements[J]. IEEE Transactions on Vehicular Technology, 2013, 62(2): 853–862. doi: 10.1109/TVT.2012.2225074 ZOU Yanbin, LIU Huaping, XIE Wei, et al. Semidefinite programming methods for alleviating sensor position error in TDOA localization[J]. IEEE Access, 2017, 5: 23111–23120. doi: 10.1109/ACCESS.2017.2752206 ZOU Yanbin, LIU Huaping, and WAN Qun. An iterative method for moving target localization using TDOA and FDOA Measurements[J]. IEEE Access, 2017, 6: 2746–2754. doi: 10.1109/ACCESS.2017.2785182 BOYD S and VANDENBERGHE L. Convex Optimization[M]. Cambridge: Cambridge University Press, 2004: 152–160. GRANT M, BOYD S, and YE Y. CVX: MATLAB software for disciplined convex programming[EB/OL]. http://cvxr.com/cvx/, 2018. -





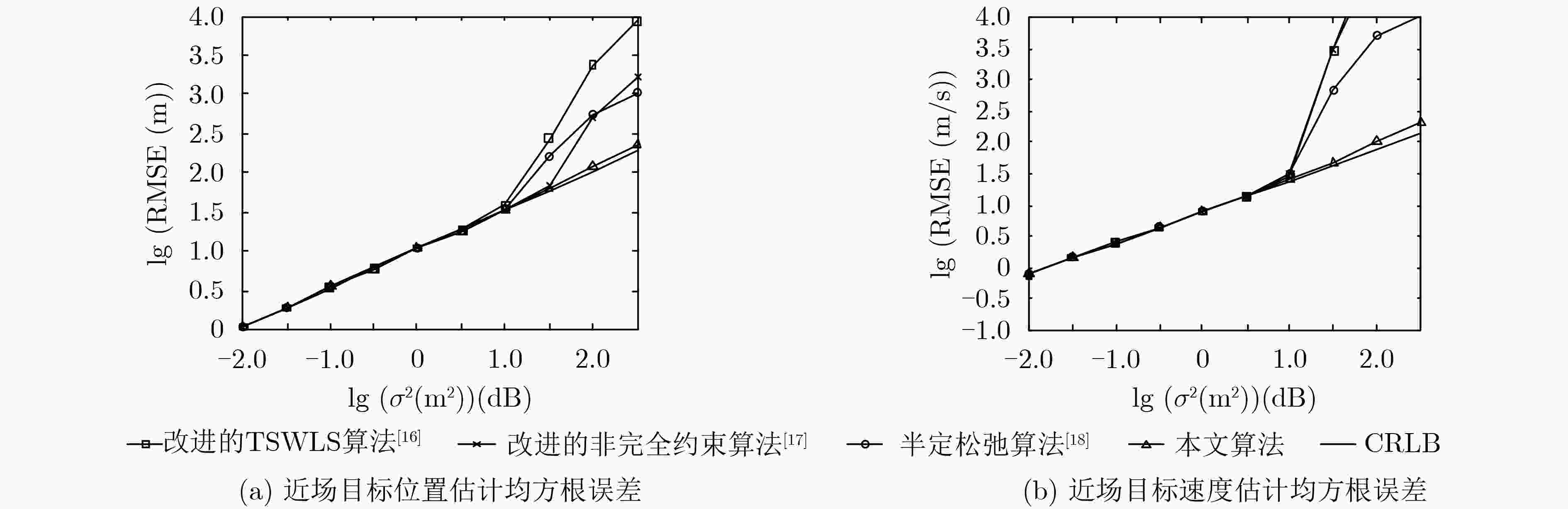
 下载:
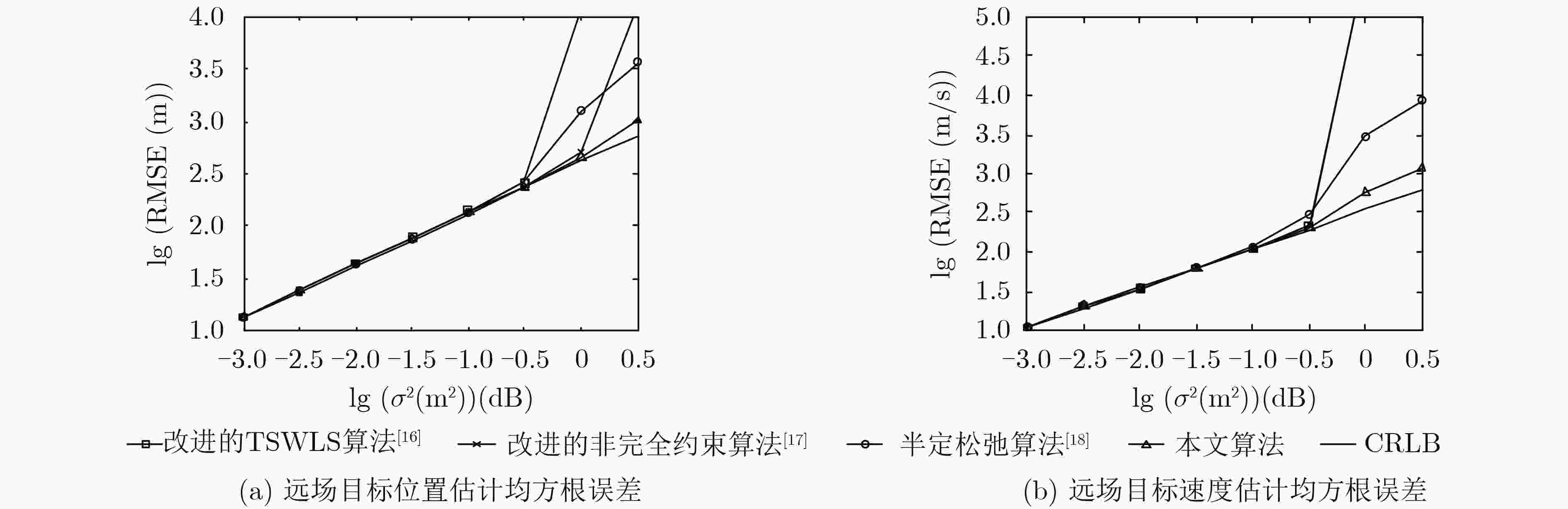
下载:
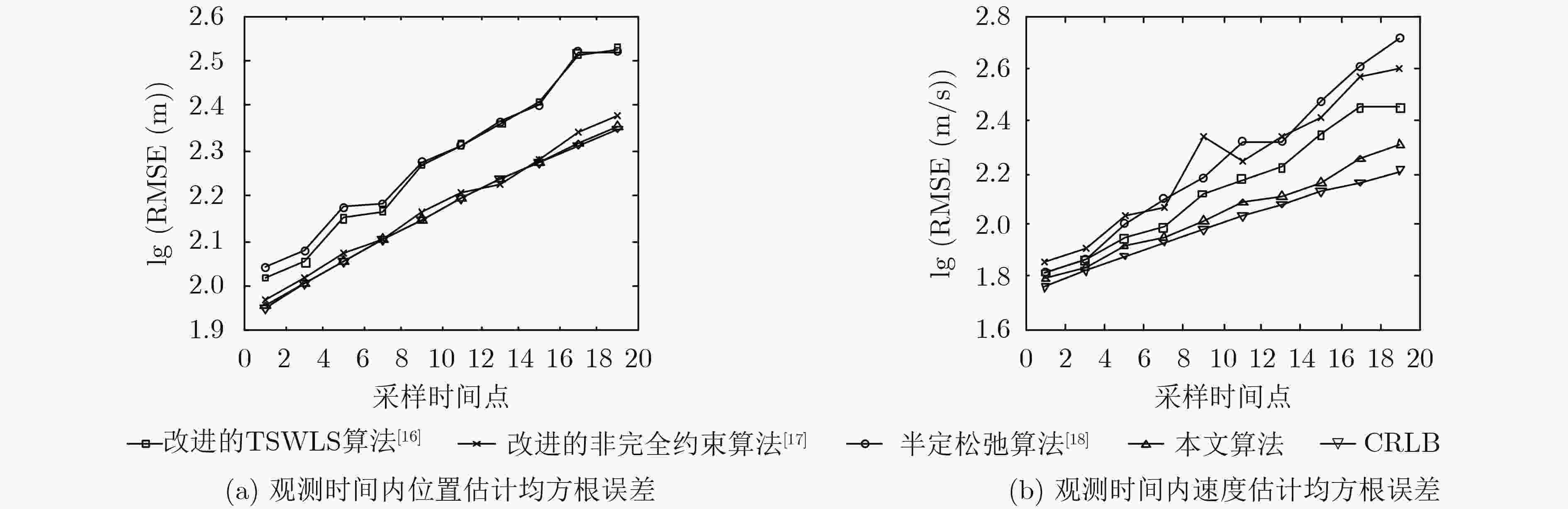


 下载:
下载:
