A Connection-oriented Fast Multi-dimensional Packet Classification Algorithm
-
摘要:
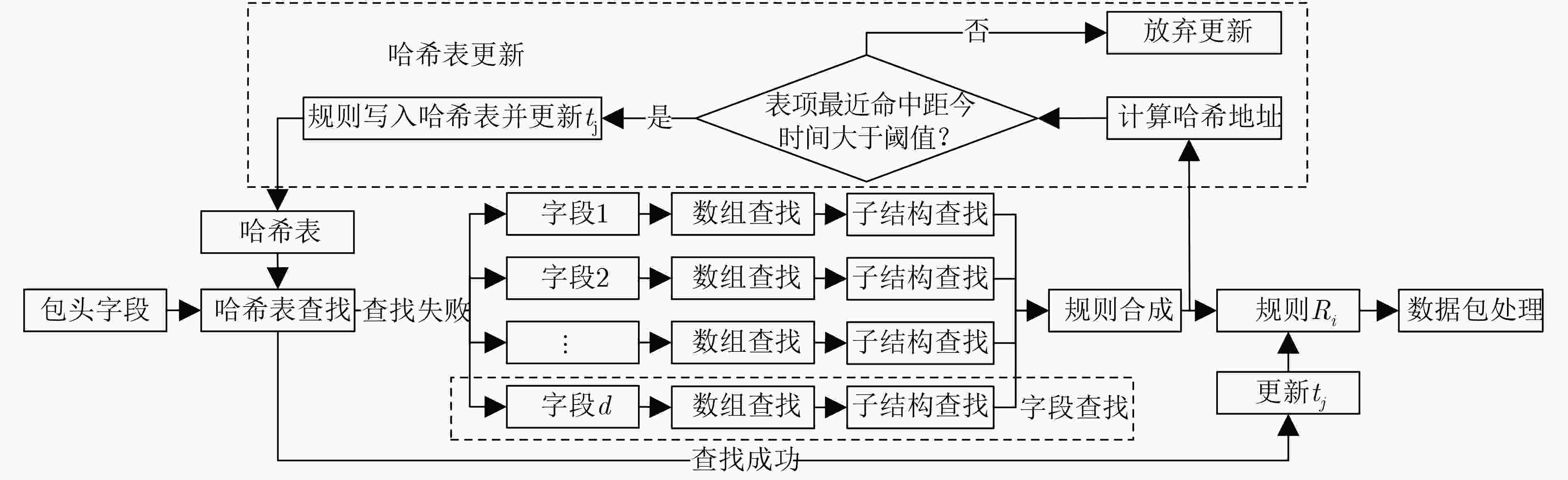
为进一步提高聚合位向量(ABV)算法分类数据包的速度,该文提出一种面向连接的改进ABV(IABV)算法。该算法利用同一连接包分类查找规则相对一致的特点,建立哈希表-规则库两级优化查找结构,首先通过哈希表查找包分类规则,若未命中继续从规则库中查找。利用连接时效性特点设计哈希表冲突处理机制,根据表项最近命中时间判断是否进行覆写更新,避免规则累积导致查找时间增加;其次对ABV算法各维度进行等分处理,为各等分区间建立数组索引,从而快速缩小向量查找范围,加快查找规则库速度;最后,将规则中前缀转化为范围降低辅助查找结构复杂度,以减少内存空间占用量并加快规则查找速度。实验结果表明,将规则中前缀转化为范围后能够有效提升算法性能,相同条件下IABV算法相比ABV算法时间性能有显著提高。
Abstract:In order to increase the classification speed of Aggregated Bit Vector (ABV) algorithm, an Improved Aggregated Bit Vector (IABV) algorithm is proposed, which is connection-oriented. Based on the characteristic that the packets which belong to the same connection have similar classification results, IABV establishes a Hash table-rule set two-level searching structure. It first searches in the Hash table to check the packet classification rule and then finds the matching rule in the rule set when the Hash table lookup fails. To avoid the accumulation of rules in the table, a collision handling mechanism is proposed. It judges whether to overwrite the Hash table entry which is collision according to the last hit time of the entry; Secondly, for the purpose of accelerate rule set searching, IABV divides each dimension into multiple intervals equally and employs array to index these intervals; Finally, the prefix in the rule is converted into range to reduce the complexity of the search structure, so that the time and memory consumption of the algorithm can be decreased. The experiment result shows that the performance of the algorithm can be improved by converting prefix into range and the time performance of IABV algorithm is significantly improved compared with the ABV algorithm under the same conditions.
-
表 1 IABV算法伪代码
输入:数据包Packet, 规则库${R_{1,2,···,N}}$ 输出:数据包匹配的规则Rule (1) ${\rm{Axis}}[1,2, ··· ,d]{\rm{ = Project}}({R_{1,2,···,N}})$//将所有规则$d$个维度分别投影到数轴上; (2) ${\rm{AxisCut}}[1,2,···,d][1,2,···,e]{\rm{ = CutDimension(Axis}}[1,2,···,d],e)$//将各维$e$等分; (3) FOR $m{\rm{ }} = {\rm{ }}1$ TO $d$; (4) FOR $n{\rm{ }} = {\rm{ }}1$ TO $e$; (5) ${\rm{Array}}[m][n] = {\rm{BuildSearchStructure}}({\rm{AxisCut}}[m][n])$//对各维等分区间建立相应数据结构对其内的投影区间进行索引,并建立数组索
引各维等分区间上的数据结构;(6) ${\rm{BuildVector(Array}}[m][n],{R_{1,2,···,N}})$//根据规则库中规则对位向量以及聚合位向量进行设置; (7) END FOR (8) END FOR (9) ${\rm{Build(HashTable}}[1,2, ··· ,S],t[1,2, ··· ,S],\sigma ,{\rm{clk}})$//建立哈希表与时钟,对哈希表每个单元设置最近命中时间${t_j}(j = 1,2,···,S)$,设置命
中时间差阈值$\sigma $并开启时钟${\rm{clk}}$;(10) WHILE PacketArrive()//接收到数据包时进行操作; (11) ${\rm{Field[1,2,}}···{\rm{,}}d{\rm{] }} = {\rm{ GetField}}\left( {{\rm{Packet}}} \right)$//取出$d$个包头字段; (12) $j = {\rm{Hash}}\left( {{\rm{Field[1,2,}}···{\rm{,}}d{\rm{]}}} \right)\% \left( {S + 1} \right)$//计算哈希地址; (13) IF ${\rm{Field[1,2,}}···{\rm{,}}d{\rm{]}} \in {\rm{HashTable[}}j{\rm{]}}$//若哈希表中存储的规则与数据包匹配,更新命中时间并返回规则; (14) ${t_j}{\rm{ = clk}}$; (15) RETURN ${\rm{HashTable[}}j{\rm{]}}$; (16) END IF (17) FOR $i{\rm{ }} = {\rm{ }}1$ TO $d$//$d$个维度分别查找向量;
(18) ${\rm{Root} }[i]{\rm{ } } = {\rm{ Array} }[i]\left[\left\lceil {{ {e*{\rm{Field} }[i]} }/{ { {\rm{Range} }({\rm{Field} }[i])} } } \right\rceil \right]$//计算字段值所在的数组单元,取出子结构根结点;(19) ${\rm{ABV}}[i][1,2, ··· ,\left\lceil {N/L} \right\rceil ],{\rm{BV}}[i][1,2,···,N] = {\rm{FindVector}}({\rm{Root}}[i],{\rm{Field}}[i])$//查找子结构,找到位向量与聚合位向量; (20) END FOR (21) $P = {\rm{ABV}}[1]\& ··· \& {\rm{ABV}}[d]$//聚合位向量按位与; (22) FOR $x = 1$ TO $P.{\rm{Length}}$//对$P$中每一位执行循环; (23) IF $P[x] = 1$//如果$P$中第$x$位为比特1; (24) ${Q_x} = {\rm{BV}}[1][L \cdot (x - 1) + 1,L \cdot (x - 1) + 2,···,L \cdot x]\& ···\& {\rm{BV}}[d][L \cdot (x - 1) + 1,L \cdot (x - 1) + 2$,
$···,L \cdot x]$//取出BV中与x对应的$L$位按位与;(25) IF ${Q_x}! = 0$; (26) $c = {Q_x}.{\rm{FirstBitPosition}}(1)$//${Q_x}$中第1个比特1的位置; (27) IF ${\rm{clk} } - {t_j} \ge \sigma $//判断规则是否写入哈希表; (28) ${\rm{HashTable[}}j{\rm{]}} = {R_{L(x - 1) + c}}$; (29) ${t_j} = {\rm{clk}}$; (30) END IF (31) RETURN ${R_{L(x - 1) + c}}$; (32) END IF (33) END IF (34) END FOR (35) RETURN ${\rm{DefaultRule}}$//返回默认规则; (36) END WHILE 表 2 算法预处理时间对比(ms)
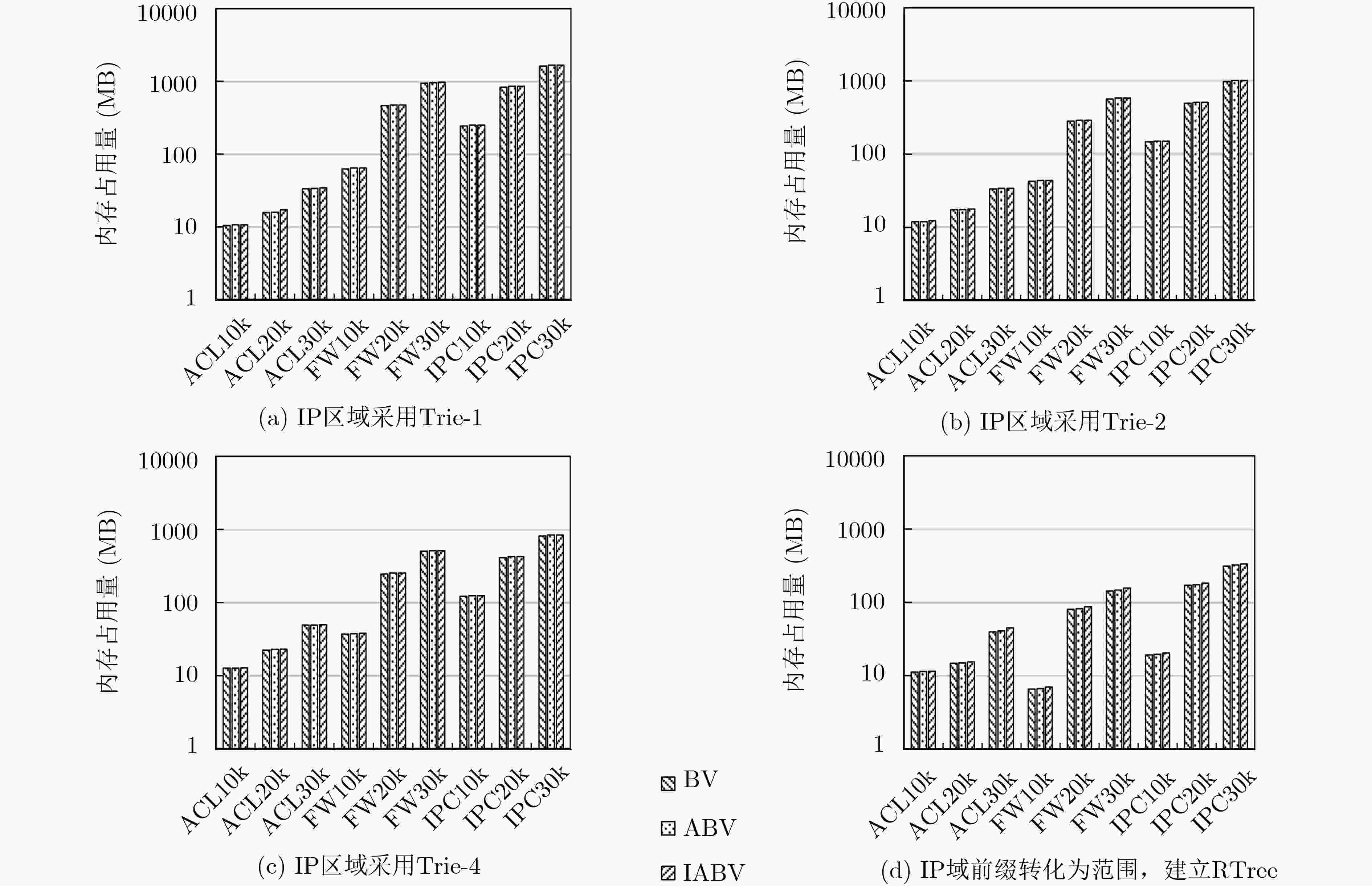
数据结构 规则库规模 10 k 20 k 30 k ACL FW IPC ACL FW IPC ACL FW IPC Trie-1 BV 1174 12540 42496 3699 106915 195698 5075 202435 430327 ABV 1192 12602 45231 3798 110567 196068 5125 209298 440421 IABV 1237 12659 45563 4101 111206 196624 5163 209871 443620 Trie-2 BV 1201 7083 25146 3453 66191 118100 4987 126026 266448 ABV 1262 7390 26131 3531 67828 118219 5043 129580 270810 IABV 1323 7536 26579 3834 68622 118793 5158 131054 272014 Trie-4 BV 1368 7182 23571 3973 62380 105742 6124 120220 242206 ABV 1396 7503 24300 4055 64571 106346 6233 123834 250471 IABV 1427 7620 24667 4151 66576 111140 6301 127998 255087 RTree BV 1069 3448 10514 3207 28270 43799 4905 56598 106005 ABV 1117 3589 10675 3273 28775 44428 4910 57610 106186 IABV 1131 3793 11095 3284 29200 44890 4996 59252 107847 表 3 算法内存访问次数对比
规则库 Trie-1 Trie-2 最小内存访问次数 最大内存访问次数 平均内存访问次数 最小内存访问次数 最大内存访问次数 平均内存访问次数 BV ABV IABV BV ABV IABV BV ABV IABV BV ABV IABV BV ABV IABV BV ABV IABV ACL 10k 78 78 5 1103 471 466 605 110 48 46 51 5 1071 450 453 579 83 40 ACL 20k 78 83 5 3273 923 919 1524 137 70 46 51 5 3241 891 895 1498 111 61 ACL 30k 46 48 5 4638 1018 1014 2181 177 88 31 35 5 4606 986 990 2154 151 79 FW 10k 41 30 5 292 278 280 145 121 57 30 27 5 267 261 268 130 106 53 FW 20k 75 57 5 3271 2256 2251 1608 621 240 46 39 5 3260 2248 2248 1592 605 236 FW 30k 75 56 5 4720 2858 2853 3045 965 197 47 39 5 4715 2852 2852 3031 951 194 IPC 10k 43 48 5 1614 658 664 824 244 75 29 34 5 1596 644 654 803 223 71 IPC 20k 73 59 5 3163 733 735 1614 219 89 43 45 5 3149 719 727 1592 197 84 IPC 30k 70 64 5 4755 1092 1097 2280 386 203 42 46 5 4727 1078 1088 2258 365 196 规则库 Trie-4 RTree 最小内存访问次数 最大内存访问次数 平均内存访问次数 最小内存访问次数 最大内存访问次数 平均内存访问次数 BV ABV IABV BV ABV IABV BV ABV IABV BV ABV IABV BV ABV IABV BV ABV IABV ACL 10k 30 35 5 1055 439 446 566 70 36 29 34 5 1054 441 448 567 71 36 ACL 20k 30 35 5 3225 875 883 1484 97 56 30 35 5 3226 876 883 1486 99 56 ACL 30k 24 28 5 4590 970 978 2141 137 74 32 37 5 4593 973 977 2145 124 74 FW 10k 24 25 5 255 252 262 122 98 51 38 42 5 269 264 260 135 110 52 FW 20k 31 30 5 3255 2244 2247 1583 596 234 37 42 5 3270 2260 2249 1595 608 236 FW 30k 32 30 5 4713 2848 2851 3023 943 192 38 42 5 4731 2866 2854 3036 957 194 IPC 10k 22 27 5 1587 637 649 793 213 68 39 44 5 1604 656 655 809 229 71 IPC 20k 28 32 5 3142 712 723 1580 185 81 41 46 5 3163 732 732 1597 202 84 IPC 30k 28 32 5 4713 1072 1084 2247 354 192 41 46 5 4733 1093 1091 2265 372 197 -
SHEN Tong, ZHANG Dafang, XIE Gaogang, et al. Optimizing multi-dimensional packet classification for multi-core systems[J]. Journal of Computer Science and Technology, 2018, 33(5): 1056–1071. doi: 10.1007/s11390-018-1873-9 BI Xiaan, LUO Xianhao, and SUN Qi. Branch tire packet classification algorithm based on single-linkage clustering[J]. Mathematics and Computers in Simulation, 2019, 155: 78–91. doi: 10.1016/j.matcom.2017.11.003 亓亚烜, 李军. 高性能网包分类理论与算法综述[J]. 计算机学报, 2013, 36(2): 408–421. doi: 10.3724/SP.J.1016.2013.00408QI Yaxuan and LI Jun. Theoretical analysis and algorithm design of high-performance packet classification algorithms[J]. Chinese Journal of Computers, 2013, 36(2): 408–421. doi: 10.3724/SP.J.1016.2013.00408 陈小雨, 陆月明. 基于多维空间动态划分与RFC的包分类改进算法[J]. 网络与信息安全学报, 2018, 4(3): 35–41. doi: 10.11959/j.issn.2096-109x.2018024CHEN Xiaoyu and LU Yueming. Improved packet classification algorithm based on multidimensional space dynamic division and RFC[J]. Chinese Journal of Network and Information Security, 2018, 4(3): 35–41. doi: 10.11959/j.issn.2096-109x.2018024 LAKSHMAN T V and STILIADIS D. High-speed policy-based packet forwarding using efficient multi-dimensional range matching[J]. ACM SIGCOMM Computer Communication Review, 1998, 28(14): 203–214. doi: 10.1145/285243.285283 万云凯, 嵩天, 刘苗苗, 等. 流量自适应的多维度包分类方法研究[J]. 计算机学报, 2017, 40(7): 1543–1555. doi: 10.11897/SP.J.1016.2017.01543WAN Yunkai, SONG Tian, LIU Miaomiao, et al. A flow adaptive multi-dimensional packet classification algorithm[J]. Chinese Journal of Computers, 2017, 40(7): 1543–1555. doi: 10.11897/SP.J.1016.2017.01543 ZHOU Shijie, QU Y R, and PRASANNA V K. Multi-core implementation of decomposition-based packet classification algorithms[J]. The Journal of Supercomputing, 2014, 69(1): 34–42. doi: 10.1007/s11227-014-1205-y ABBASI M, TAHOURI R, and RAFIEE M. Enhancing the performance of the aggregated bit vector algorithm in network packet classification using GPU[J]. PeerJ Computer Science, 2019, 5: e185. doi: 10.7717/peerj-cs.185 BABOESCU F and VARGHESE G. Scalable packet classification[J]. IEEE/ACM Transactions on Networking, 2005, 13(1): 2–14. doi: 10.1109/TNET.2004.842232 贺亚威, 侯整风, 吴亮亮. 一种基于位向量流分类算法的改进[J]. 合肥工业大学学报: 自然科学版, 2015, 38(3): 331–335. doi: 10.3969/j.issn.1003-5060.2015.03.009HE Yawei, HOU Zhengfeng, and WU Liangliang. An improved flow classification algorithm based on bit vector[J]. Journal of Hefei University of Technology:Natural Science, 2015, 38(3): 331–335. doi: 10.3969/j.issn.1003-5060.2015.03.009 李林. 防火墙规则集关键技术研究[D]. [博士论文], 电子科技大学, 2009.LI Lin. Research on key techniques of firewall rule set[D]. [Ph.D. dissertation], University of Electronic Science and Technology of China, 2009. CAIDA. The CAIDA UCSD anonymized internet traces 2016[EB/OL]. http://www.caida.org/data/passive/passive_2016_dataset.xml, 2016. 颜天信, 王永纲, 石江涛, 等. 区域分割包分类算法的优化实现[J]. 通信学报, 2004, 25(6): 80–88. doi: 10.3321/j.issn:1000-436X.2004.06.011YAN Tianxin, WANG Yonggang, SHI Jiangtao, et al. Optimized implementation of regional partition algorithm for packet classification[J]. Journal of China Institute of Communications, 2004, 25(6): 80–88. doi: 10.3321/j.issn:1000-436X.2004.06.011 TAYLOR D E and TURNER J S. ClassBench: A packet classification benchmark[C]. Proceedings of the IEEE 24th Annual Joint Conference of the IEEE Computer and Communications Societies, Miami, USA, 2005: 2068–2079. doi: 10.1109/INFCOM.2005.1498483. 孙鹏浩, 兰巨龙, 陆肖元, 等. 一种基于匹配域裁剪的包分类规则集压缩方法[J]. 电子与信息学报, 2017, 39(5): 1185–1192. doi: 10.11999/JEIT160740SUN Penghao, LAN Julong, LU Xiaoyuan, et al. Field-trimming compression model for rule set of packet classification[J]. Journal of Electronics &Information Technology, 2017, 39(5): 1185–1192. doi: 10.11999/JEIT160740 -





 下载:
下载:


 下载:
下载:
