Low-elevation DOA Estimation for VHF Radar Based on Multi-frame Phase Feature Enhancement
-
摘要:
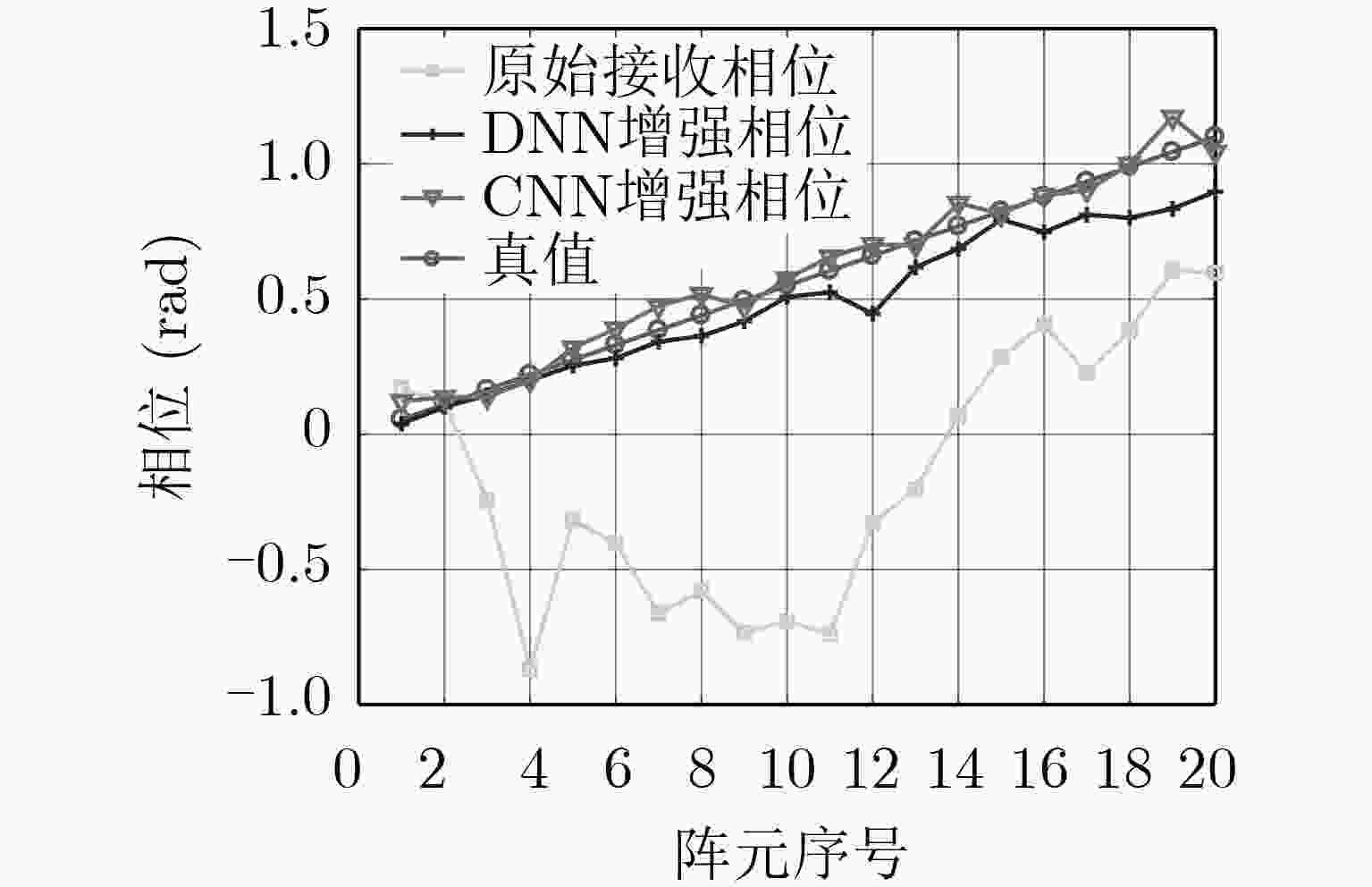
针对米波雷达低仰角目标的DOA估计问题,该文提出一种新的基于多帧相位特征增强方法,所提方法可以有效解决低仰角条件下阵列接收信号中直达信号相位特征模糊问题,进而提高DOA估计精度。通过学习多帧原始数据的相位分布特征与理想环境下直达波信号的相位分布特征之间的复杂映射关系,有效削弱多径信号引起的相位误差,将增强后的相位信息与原始的幅度信息进行数据重组,并利用已有的超分辨算法进行DOA估计。通过计算机仿真实验和实测数据验证,该文所提方法在DOA估计性能以及泛化能力上优于基于物理驱动的MUSIC算法以及数据驱动的基于特征反演和基于支持向量回归的两种估计方法。
Abstract:For the DOA estimation problem of low-elevation target of VHF radar, a new multi-frame phase feature enhancement based method is proposed, which solves effectively the phase feature ambiguity of direct signal, and thus improves the accuracy of DOA estimation. By learning the complex mapping relationship between the phase distribution of the multi-frame data and ideal phase distribution of the direct signal, the fuzzy phase information is enhanced and is used to reconstruct a new data matrix with original amplitude information. The DOA is estimated by conventional methods using new data matrix, which effectively improves the DOA estimation accuracy of the low-elevation target. The effectiveness of proposed method is validated by computer simulation experiments and real data, and it shows higher accuracy compared with physics-driven methods including MUSIC method and state-of-the-art data-driven method including feature reversal and Support Vector Regression (SVR).
-
表 1 深度神经网络结构配置
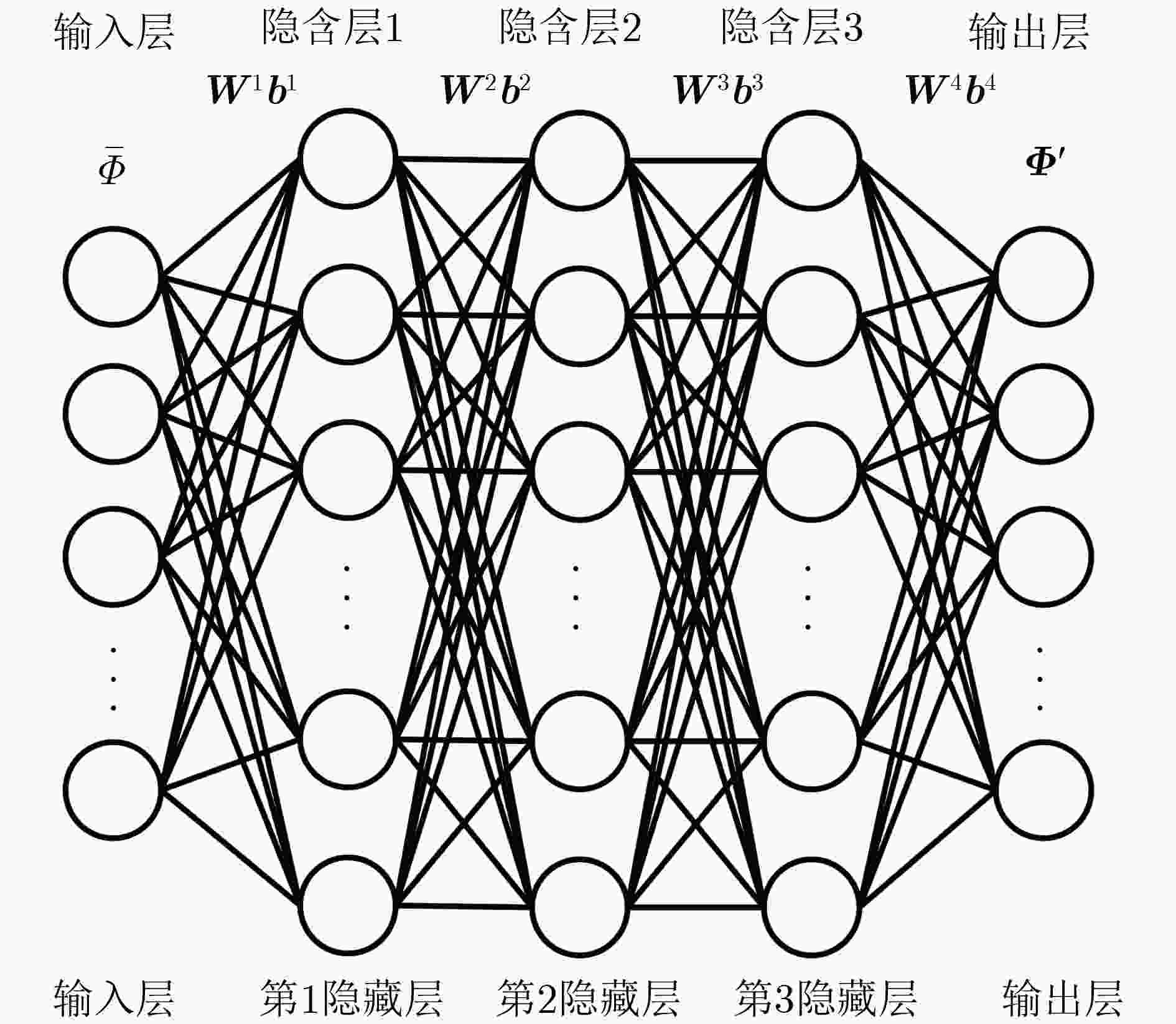
网络结构 激活函数 学习率 初始化方式 ${{x}} \times 1024 \times 1024 \times 1024 \times {{o}}$ ReLU 10–4 高斯随机初始化 表 2 深度卷积神经网络结构配置
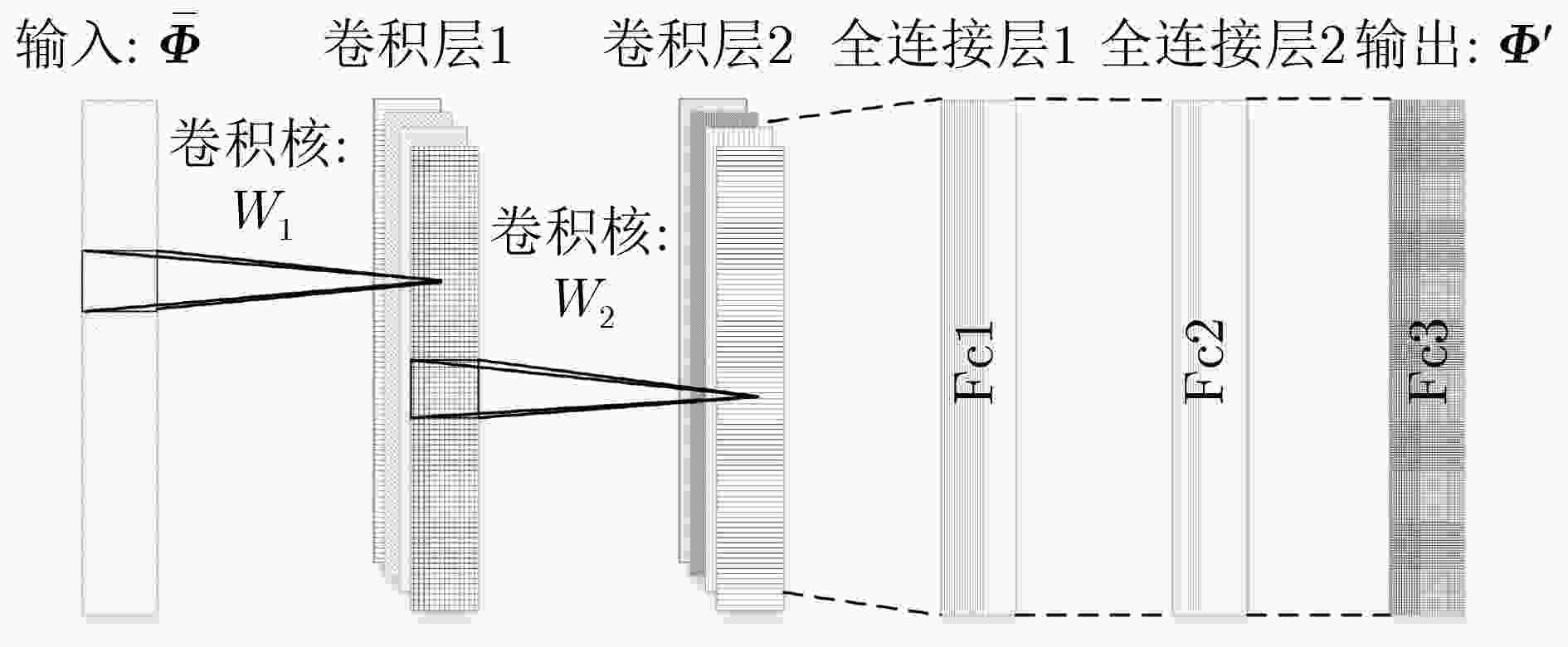
网络结构 卷积核大小 池化层大小 激活函数 学习率 初始化方式 2层卷积层 $3 \times 1 \times 15$ $1 \times 3$ ReLU 10–4 高斯随机 3层全连接层 $3 \times 15 \times 30$ 初始化 表 3 有效点数占比(%)
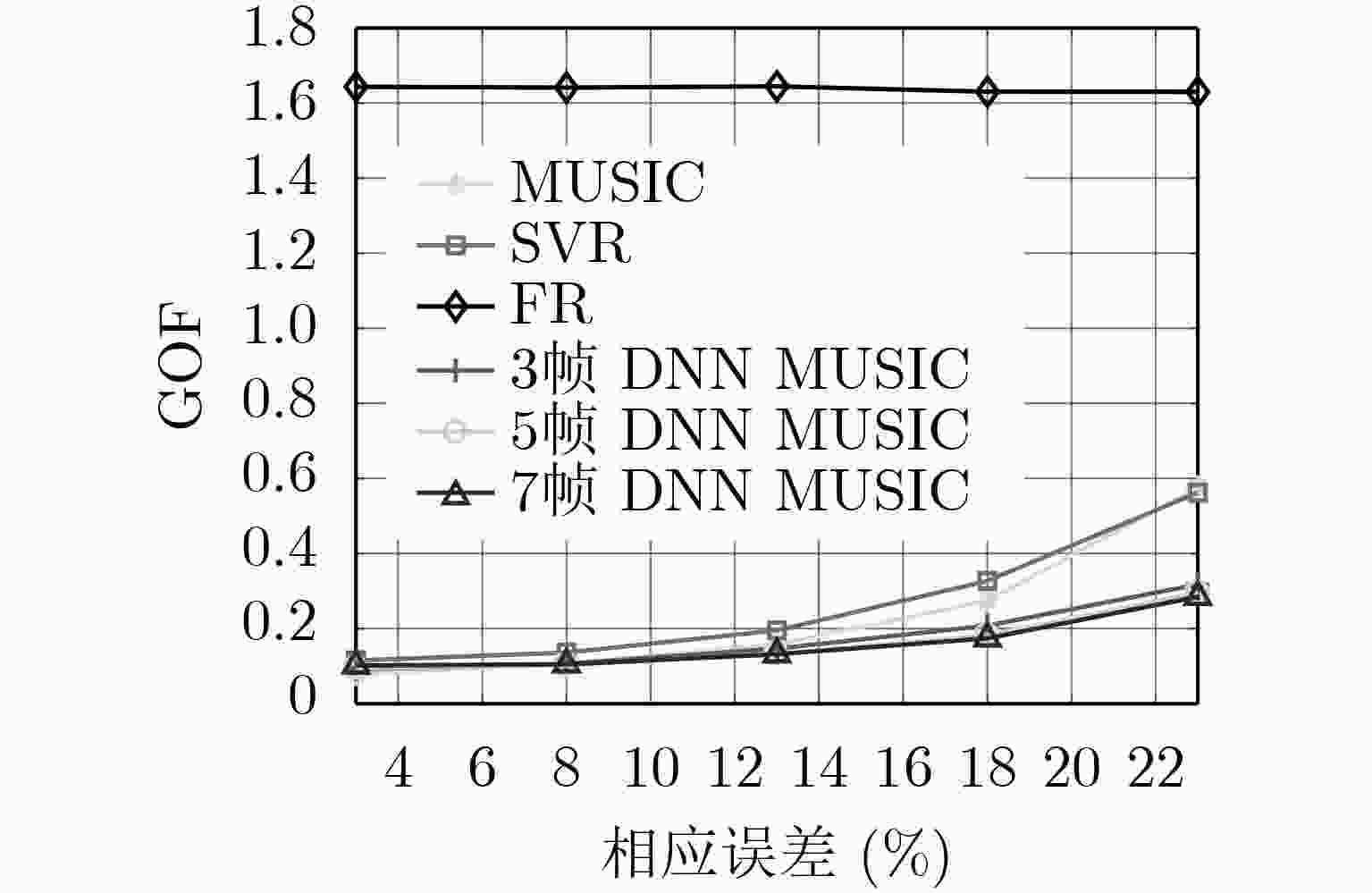
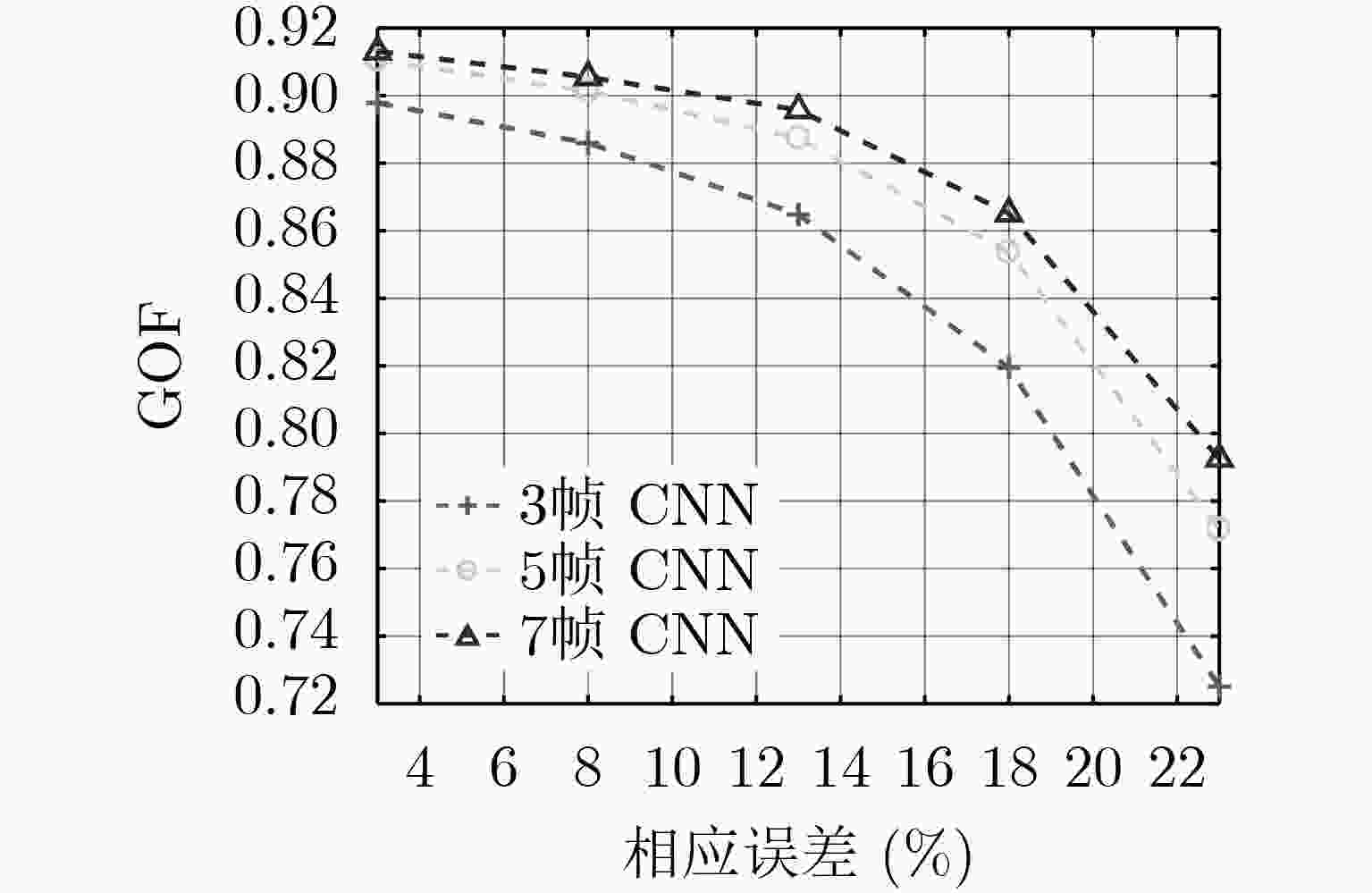
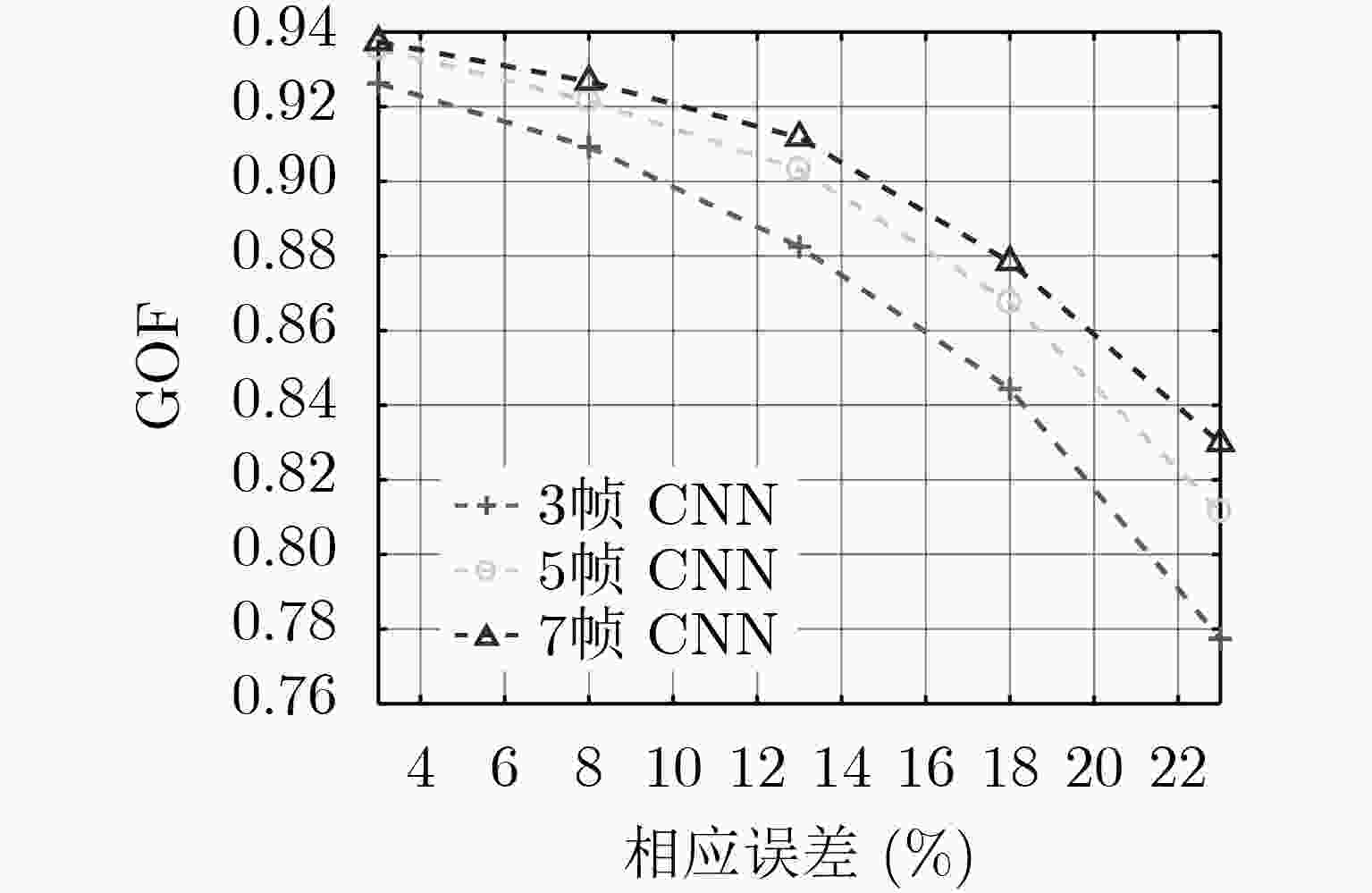
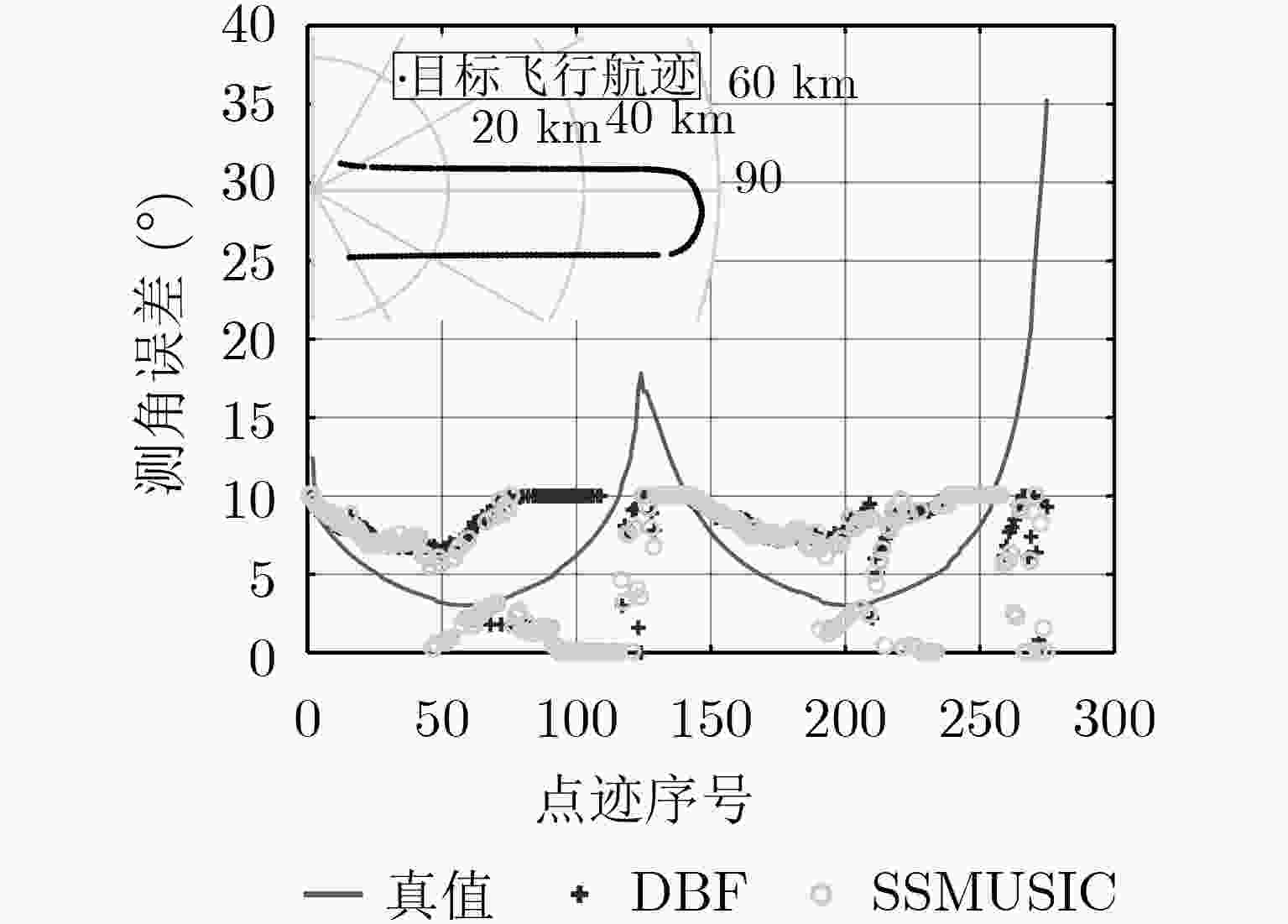
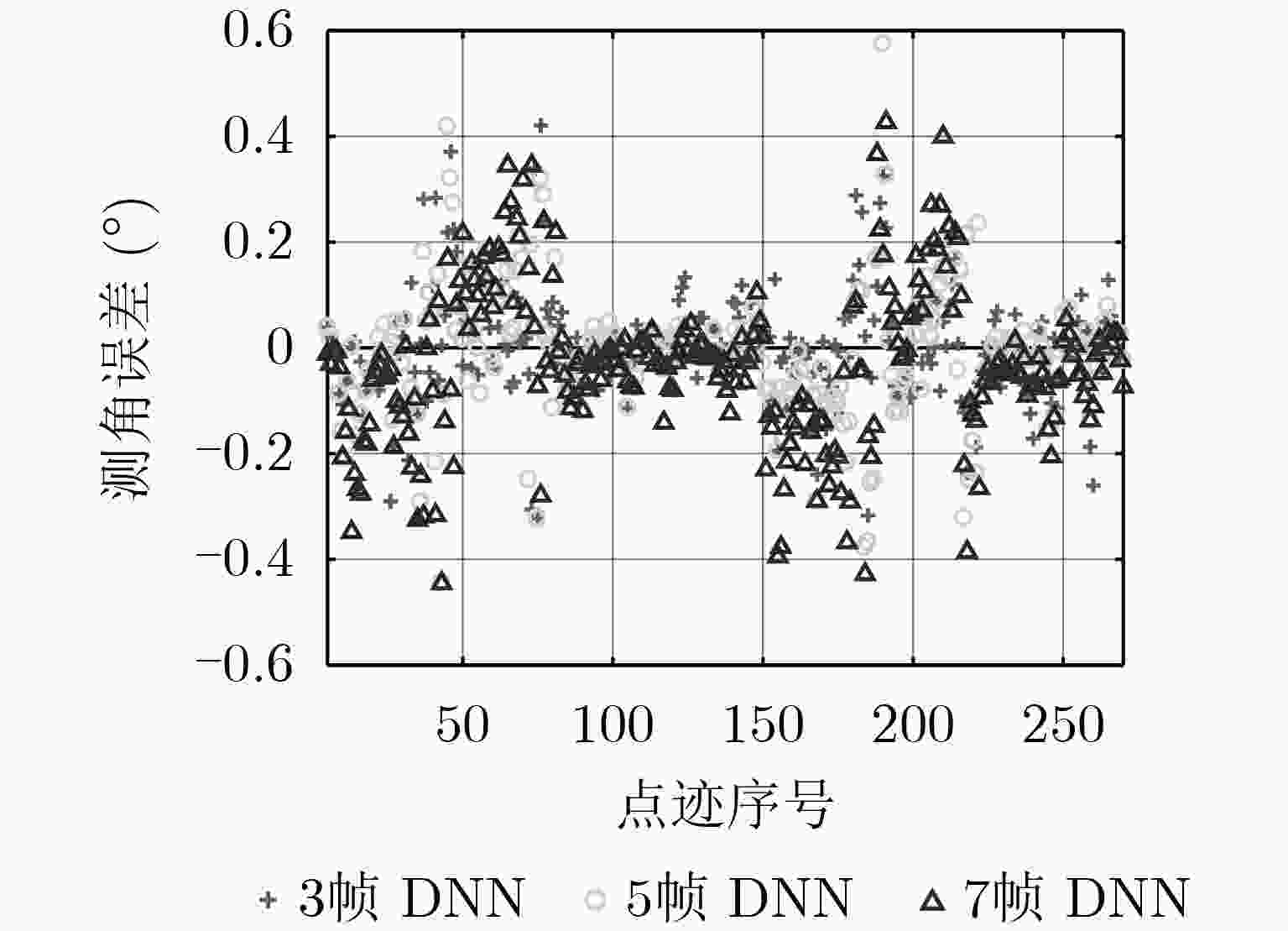
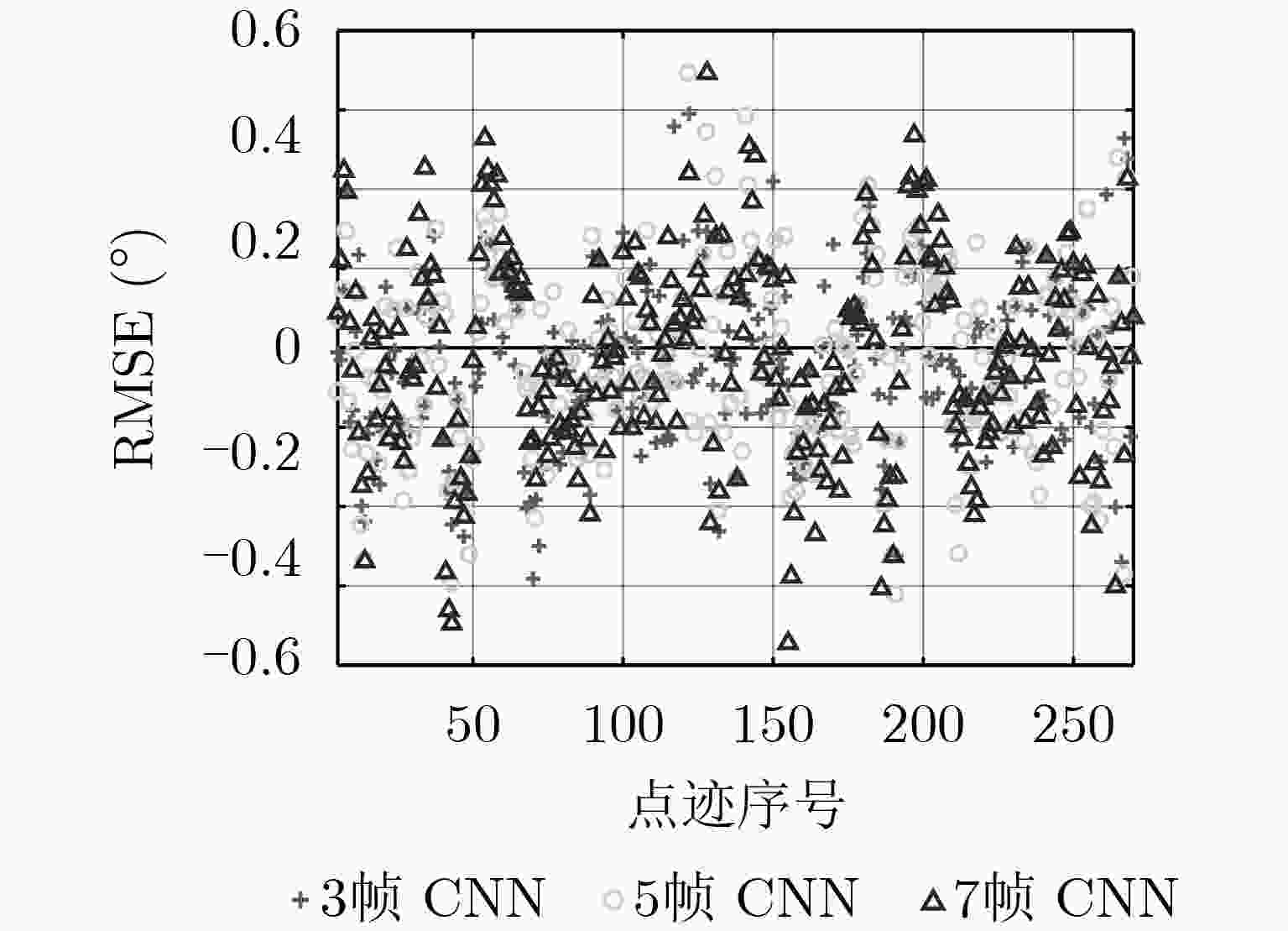
方法 DBF SSMUSIC 3帧DNN 5帧DNN 7帧DNN 3帧CNN 5帧CNN 7帧CNN 占比 1.8 0.2 95.6 93.5 89.8 85.1 81.1 72.7 -
朱伟. 米波数字阵列雷达低仰角测高方法研究[D]. [博士论文], 西安电子科技大学, 2013.ZHU Wei. Study on low-angle altitude measurement in VHF Radar[D]. [Ph.D. dissertation], Xidian University, 2013. 郑轶松. 米波阵列雷达低仰角测高若干问题研究[D]. [博士论文], 西安电子科技大学, 2017.ZHENG Yisong. Study on some issues of low-angle altitude measurement for VHF array radar[D]. [Ph.D. dissertation], Xidian University, 2017. 李存勖. 米波雷达低仰角测高相关问题研究[D]. [博士论文], 西安电子科技大学, 2018.LI Cunxu. Study on some issues of altitude measurement of low-angle target for VHF array radar[D]. [Ph.D. dissertation], Xidian University, 2018. 陈伯孝, 胡铁军, 郑自良, 等. 基于波瓣分裂的米波雷达低仰角测高方法及其应用[J]. 电子学报, 2007, 35(6): 1021–1025. doi: 10.3321/j.issn:0372-2112.2007.06.003CHEN Baixiao, HU Tiejun, ZHENG Ziliang, et al. Method of altitude measurement based on beam Split in VHF radar and its application[J]. Acta Electronica Sinica, 2007, 35(6): 1021–1025. doi: 10.3321/j.issn:0372-2112.2007.06.003 ZHU Wei and CHEN Baixiao. Altitude measurement based on terrain matching in VHF array radar[J]. Circuits, Systems, and Signal Processing, 2013, 32(2): 647–662. doi: 10.1007/s00034-012-9472-4 郑轶松, 陈伯孝. 米波雷达低仰角目标多径模型及其反演方法研究[J]. 电子与信息学报, 2016, 38(6): 1468–1474. doi: 10.11999/JEIT151013ZHENG Yisong and CHEN Baixiao. Multipath model and inversion method for low-angle target in very high frequency radar[J]. Journal of Electronics &Information Technology, 2016, 38(6): 1468–1474. doi: 10.11999/JEIT151013 SCHMIDT R. Multiple emitter location and signal parameter estimation[J]. IEEE Transactions on Antennas and Propagation, 1986, 34(3): 276–280. doi: 10.1109/TAP.1986.1143830 ROY R and KAILATH T. ESPRIT-estimation of signal parameters via rotational invariance techniques[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1989, 37(7): 984–995. doi: 10.1109/29.32276 ZISKIND I and WAX M. Maximum likelihood localization of multiple sources by alternating projection[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1988, 36(10): 1553–1560. doi: 10.1109/29.7543 CHOI Y H. Alternating projection for maximum-likelihood source localization using eigendecomposition[J]. IEEE Signal Processing Letters, 1999, 6(4): 73–75. doi: 10.1109/97.752057 WU Bo, LI Kehuang, GE Fengpei, et al. An end-to-end deep learning approach to simultaneous speech dereverberation and acoustic modeling for robust speech recognition[J]. IEEE Journal of Selected Topics in Signal Processing, 2017, 11(8): 1289–1300. doi: 10.1109/JSTSP.2017.2756439 WU Bo, LI Kehuang, YANG Minglei, et al. A reverberation-time-aware approach to speech dereverberation based on deep neural networks[J]. IEEE/ACM Transactions on Audio, Speech, and Language Processing, 2017, 25(1): 102–111. doi: 10.1109/TASLP.2016.2623559 XIANG Houhong, CHEN Baixiao, YANG Minglei, et al. Altitude measurement based on characteristics reversal by deep neural network for VHF radar[J]. IET Radar, Sonar & Navigation, 2019, 13(1): 98–103. doi: 10.1049/iet-rsn.2018.5121 WU Liuli and HUANG Zhitao. Coherent SVR learning for wideband direction-of-arrival estimation[J]. IEEE Signal Processing Letters, 2019, 26(4): 642–646. doi: 10.1109/LSP.2019.2901641 WERBOS P J. Backpropagation through time: What it does and how to do it[J]. Proceedings of the IEEE, 1990, 78(10): 1550–1560. doi: 10.1109/5.58337 LECUN Y, BOSER B, DENKER J S, et al. Backpropagation applied to handwritten zip code recognition[J]. Neural Computation, 1989, 1(4): 541–551. doi: 10.1162/neco.1989.1.4.541 KINGMA D P and BA J. Adam: A method for stochastic optimization[J]. arXiv: 2014, 1412.6980. SRIVASTAVA N, HINTON G, KRIZHEVSKY A, et al. Dropout: A simple way to prevent neural networks from overfitting[J]. Journal of Machine Learning Research, 2014, 15(1): 1929–1958. -





 下载:
下载:




 下载:
下载:
