Interference Efficiency-based Base Station Selection and Power Allocation Algorithm for Multi-cell Heterogeneous Wireless Networks
-
摘要:
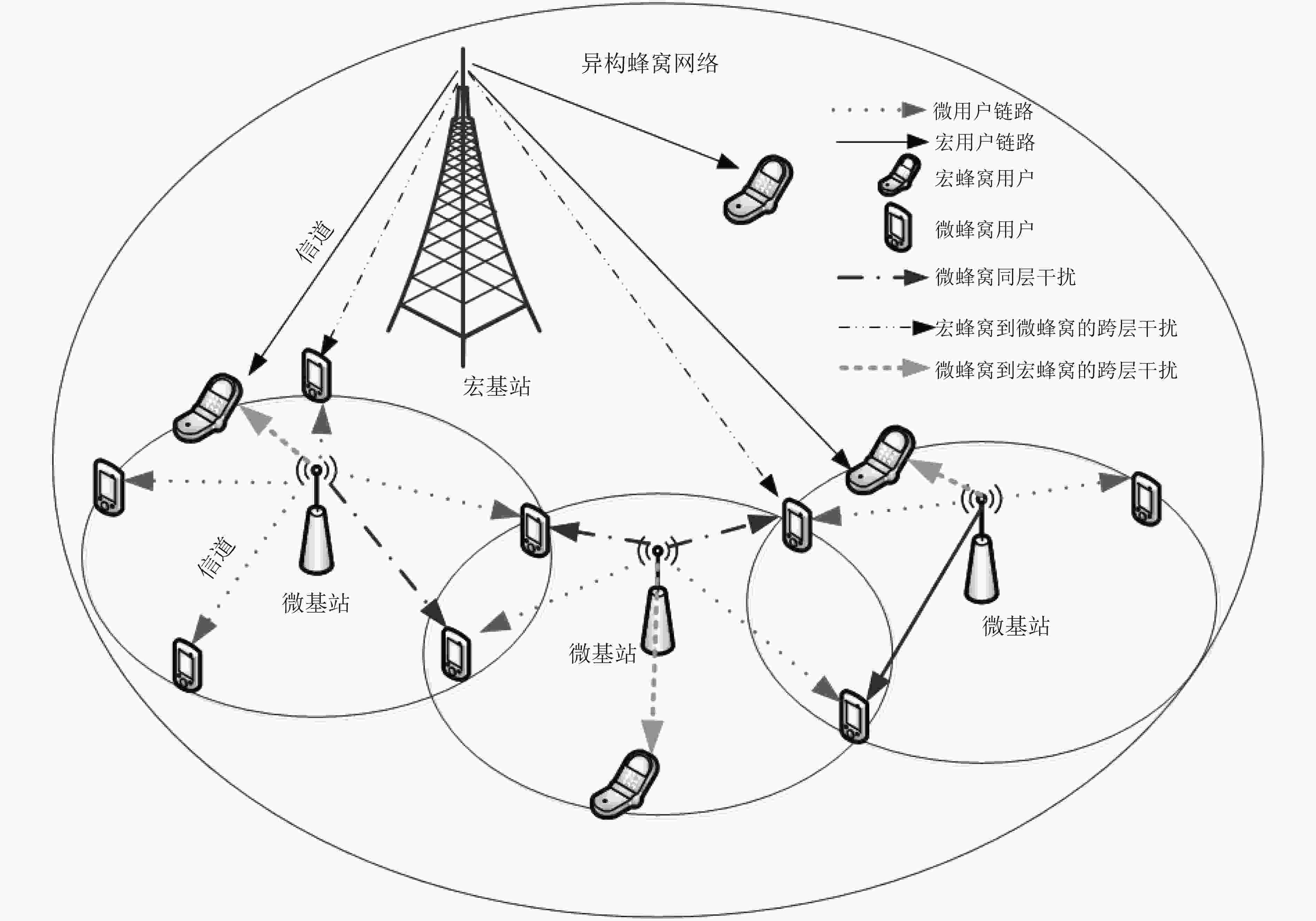
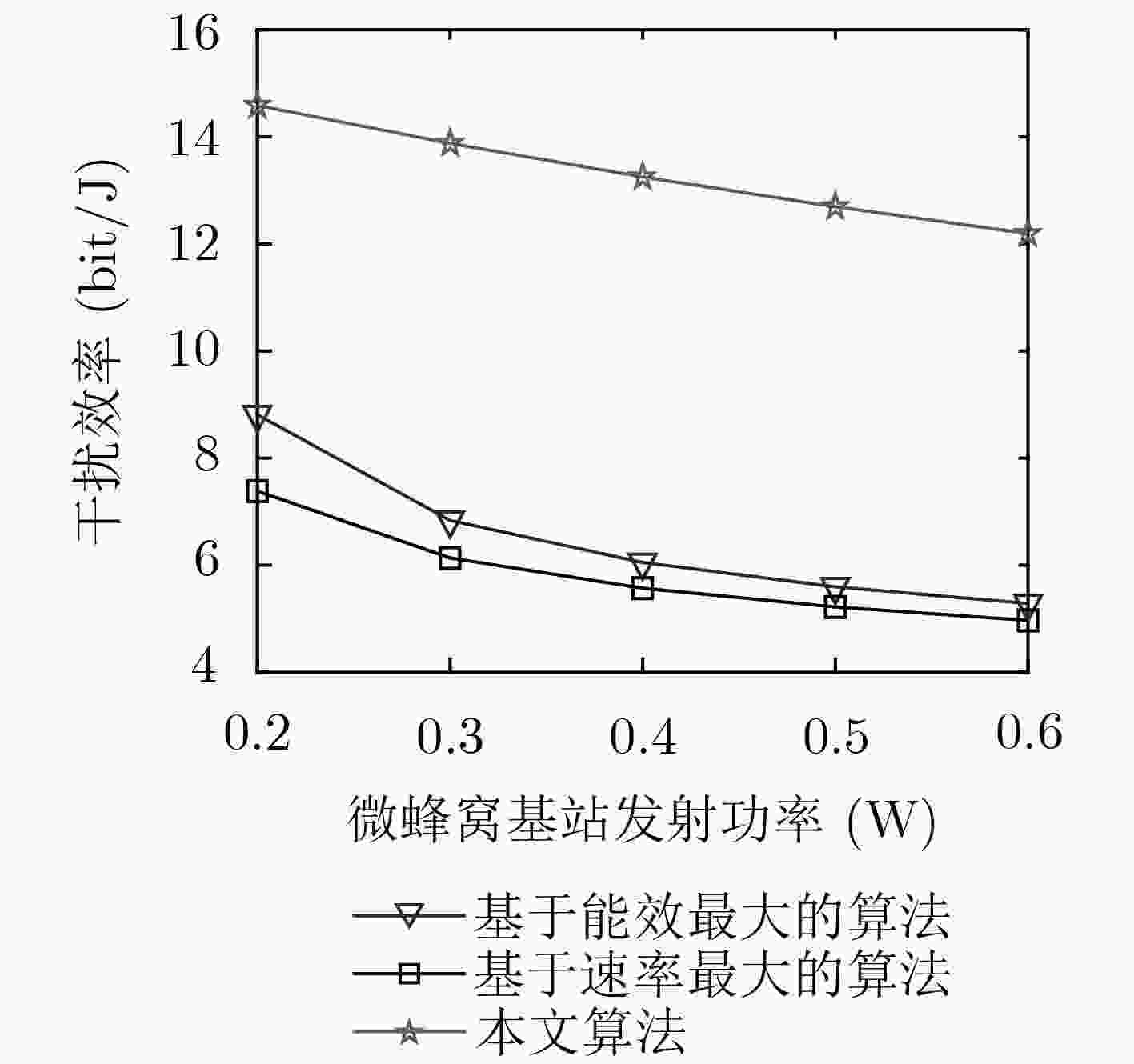
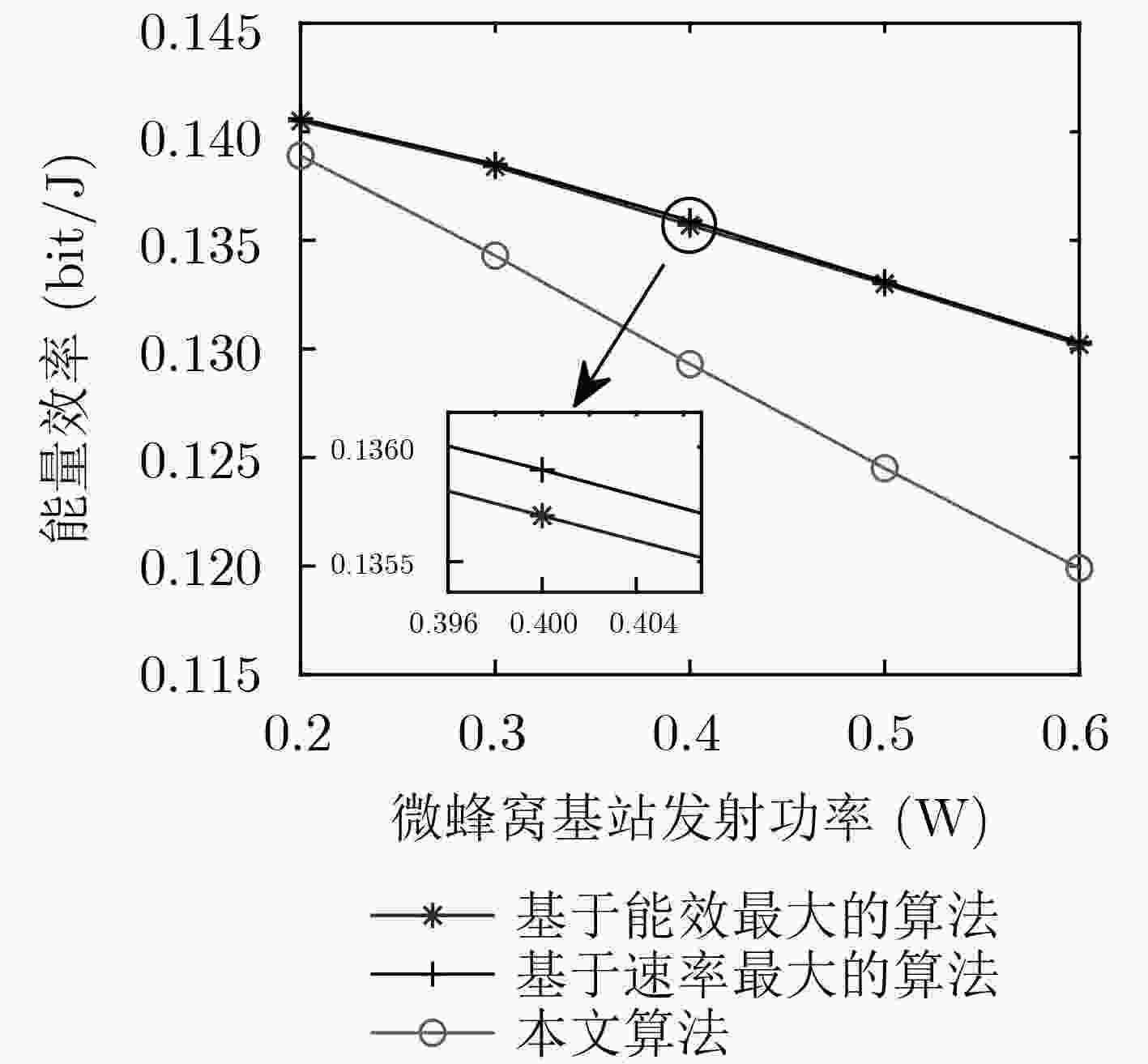
针对多蜂窝多用户异构无线网络干扰管理和效率提升问题,该文研究了基于干扰效率最大的下行链路基站(BS)-用户匹配和功率分配问题。首先,考虑宏用户和微蜂窝用户的服务质量,将问题建模为多变量混合整数非线性规划问题。其次将原问题分解为基站选择和功率分配两个子问题。针对基站选择问题,利用凸优化问题获得最优基站选择策略;针对功率分配问题,利用二次变换法和Dinkelbach辅助变量法,将功率分配问题转换为凸优化问题求解。仿真结果表明,与现有算法对比,该算法具有较好的干扰效率和干扰控制性能。
Abstract:To solve interference management and efficiency improvement of multi-cell multi-user heterogeneous wireless networks, the downlink Base Station (BS)-user matching and power allocation problem are studied to maximize the interference efficiency of femtocells. Firstly, consideration of quality of service of macro cell users and femtocell users, the problem is formulated as a multivariate mixed integer nonlinear programming problem. Secondly, the problem is decomposed into two subproblems. The BS selection problem is solved by convex optimization technique. The power allocation problem is firstly converted into a convex one by using quadratic transformation method and Dinkelbach approach, then the problem is resolved by using Lagrange dual methods and subgradient methods. Simulations results show the effectiveness of the proposed algorithm by comparing with the existing algorithms in terms of interference efficiency and interference management.
-
表 1 基站-用户匹配选择算法
初始化微蜂窝网络能服务的最大用户数${K^n}$,最小用户速率需求门限$R_{n,k}^{\min }$和发射功率${p_n}(t) = {p_0}$; 初始化拉格朗日乘子${\beta _k}(0) = {\beta _{k,0}}$, ${\chi _n}(0) = {\chi _{n,0}}$和${\lambda _{n,k}}(0) = {\lambda _{n,k,0}}$;初始化网络用户数量和基站用户数$M,N$和$K$;初始化
步长${s_1}(t),{s_2}(t)$和${s_3}(t)$。初始化第$n$个微蜂窝所接入用户数量集合为${U_n} = \varnothing $, $\left| {{U_n}} \right|$为集合中有多少个元素。While $t \le {T^{\max } }$或者${\left\| { {\varphi }(t + 1) - {\varphi }(t)} \right\|_2} \le \varepsilon $;其中${T^{\max }}$为最大迭代次数;$\varepsilon $为拉格朗日乘子收敛精度;${\varphi }(t) = {[{\beta _k}(t),{\chi _n}(t),{\lambda _{n,k} }(t)]^{\rm{T} } }$。 For k=1:1:K For n=1:1:N if $\left| { {U_n} } \right| \le {K^n}$ 根据式(9)计算${n^*}$,从而根据式(8)计算${\alpha _{n,k}}$;根据式(10)—式(12)更新拉格朗日乘子。 Else Break; End if End For 将用户编号$k$存储在${U_n}$中。 End For End while 表 2 最优功率分配算法
初始化微蜂窝网络能服务的最大用户数${K^n}$,最小用户速率需求门限$R_{n,k}^{\min }$和发射功率${p_n}(t) = {p_0}$; 初始化拉格朗日乘子,网络用户数量和基站用户数,初始化步长和干扰效率。
While $j \le J$ 或者$\left| {\dfrac{ {\displaystyle\sum\nolimits_{n = 1}^N {\displaystyle\sum\nolimits_{k = 1}^K { {\alpha _{n,k} }{R_{n,k} }(j)} } } }{ {\displaystyle\sum\nolimits_{m = 1}^M {\displaystyle\sum\nolimits_{n = 1}^N { {p_n}(j){h_{n,m} } } } } } - \eta (j - 1)} \right| > \varepsilon $;其中${T^{\max }}$为最大迭代次数;$\varepsilon $为收敛精度;For m=1:1:M For k=1:1:K For n=1:1:N 根据式(21)、式(22)计算变量${x_{n,k}}$和最优功率${p_n}$; 根据式(23)—式(25)更新拉格朗日乘子${\theta _n},{\mu _m},\lambda _{n,m}^{{p} }$。 End For End For End For Until $t = {T_{\max }}$或收敛。
更新 $j = j + 1$和$\eta (j) = \frac{ {\displaystyle\sum\nolimits_{n = 1}^N {\displaystyle\sum\nolimits_{k = 1}^K { {\alpha _{n,k} }{R_{n,k} }(j - 1)} } } }{ {\displaystyle\sum\nolimits_{m = 1}^M {\sum\nolimits_{n = 1}^N { {p_n}(j - 1){h_{n,m} } } } } }$。End while -
DAMNJANOVIC A, MONTOJO J, WEI Yongbin, et al. A survey on 3GPP heterogeneous networks[J]. IEEE Wireless Communications, 2011, 18(3): 10–21. doi: 10.1109/MWC.2011.5876496 徐勇军, 李国权, 徐鹏, 等. 异构无线网络资源分配算法研究综述[J]. 重庆邮电大学学报: 自然科学版, 2018, 30(3): 289–299. doi: 10.3979/j.issn.1673-825X.2018.03.001XU Yongjun, LI Guoquan, XU Peng, et al. Survey on resource allocation in heterogeneous wireless network[J]. Journal of Chongqing University of Posts and Telecommunications:Natural Science Edition, 2018, 30(3): 289–299. doi: 10.3979/j.issn.1673-825X.2018.03.001 ZHANG Haijun, LIU Hao, CHENG Julian, et al. Downlink energy efficiency of power allocation and wireless backhaul bandwidth allocation in heterogeneous small cell networks[J]. IEEE Transactions on Communications, 2018, 66(4): 1705–1716. doi: 10.1109/TCOMM.2017.2763623 XIE Renchao, YU F R, JI Hong, et al. Energy-efficient resource allocation for heterogeneous cognitive radio networks with femtocells[J]. IEEE Transactions on Wireless Communications, 2012, 11(11): 3910–3920. doi: 10.1109/TWC.2012.092112.111510 BACCI G, BELMEGA E V, MERTIKOPOULOS P, et al. Energy-aware competitive power allocation for heterogeneous networks under QoS constraints[J]. IEEE Transactions on Wireless Communications, 2015, 14(9): 4728–4742. doi: 10.1109/TWC.2015.2425397 LI Rui, CAO Ning, MAO Minghe, et al. Load-aware energy efficiency with unequal user priority in downlink heterogeneous network system[J]. IEEE Access, 2019, 7: 106275–106283. doi: 10.1109/ACCESS.2019.2920149 MIAO Jie, HU Zheng, YANG Kun, et al. Joint power and bandwidth allocation algorithm with QoS support in heterogeneous wireless networks[J]. IEEE Communications Letters, 2012, 16(4): 479–481. doi: 10.1109/LCOMM.2012.030512.112304 CHOI Y, KIM H, HAN S W, et al. Joint resource allocation for parallel multi-radio access in heterogeneous wireless networks[J]. IEEE Transactions on Wireless Communications, 2010, 9(11): 3324–3329. doi: 10.1109/TWC.2010.11.100045 FOOLADIVANDA D and ROSENBERG C. Joint resource allocation and user association for heterogeneous wireless cellular networks[J]. IEEE Transactions on Wireless Communications, 2013, 12(1): 248–257. doi: 10.1109/TWC.2012.121112.120018 NGO D T, KHAKUREL S, and LE-NGOC T. Joint subchannel assignment and power allocation for OFDMA femtocell networks[J]. IEEE Transactions on Wireless Communications, 2014, 13(1): 342–355. doi: 10.1109/TWC.2013.111313.130645 BOYD S and VANDENBERGHE L. Convex Optimization[M]. Cambridge, UK: Cambridge University Press, 2004. SHEN Kaiming and YU Wei. Fractional programming for communication systems-Part I: Power control and beamforming[J]. IEEE Transactions on Signal Processing, 2018, 66(10): 2616–2630. doi: 10.1109/TSP.2018.2812733 FANG Fang, DING Zhiguo, LIANG Wei, et al. Optimal energy efficient power allocation with user fairness for uplink MC-NOMA systems[J]. IEEE Wireless Communications Letters, 2019, 8(4): 1133–1136. doi: 10.1109/LWC.2019.2908912 XU Yongjun, LI Guoquan, YANG Yang, et al. Robust resource allocation and power splitting in SWIPT enabled heterogeneous networks: A robust minimax approach[J]. IEEE Internet of Things Journal, 2019, 6(6): 10799–10811. doi: 10.1109/JIOT.2019.2941897 XU Quansheng, LI Xi, JI Hong, et al. Energy-efficient resource allocation for heterogeneous services in OFDMA downlink networks: Systematic perspective[J]. IEEE Transactions on Vehicular Technology, 2014, 63(5): 2071–2082. doi: 10.1109/TVT.2014.2312288 WANG Haining, WANG Jiaheng, and DING Zhi. Distributed power control in a two-tier heterogeneous network[J]. IEEE Transactions on Wireless Communications, 2015, 14(12): 6509–6523. doi: 10.1109/TWC.2015.2456055 -





 下载:
下载:



 下载:
下载:
