Virus Propagation Model and Security Performance Optimization Strategy of Multi-operating System Heterogeneous Network
-
摘要:
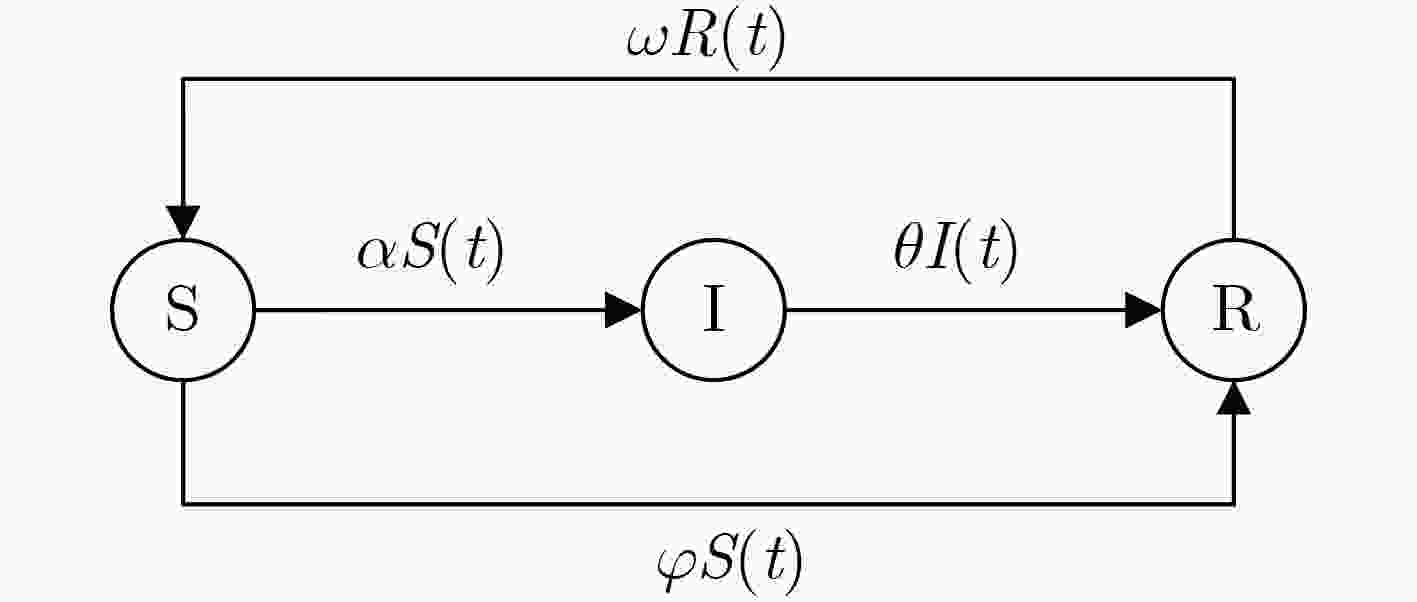
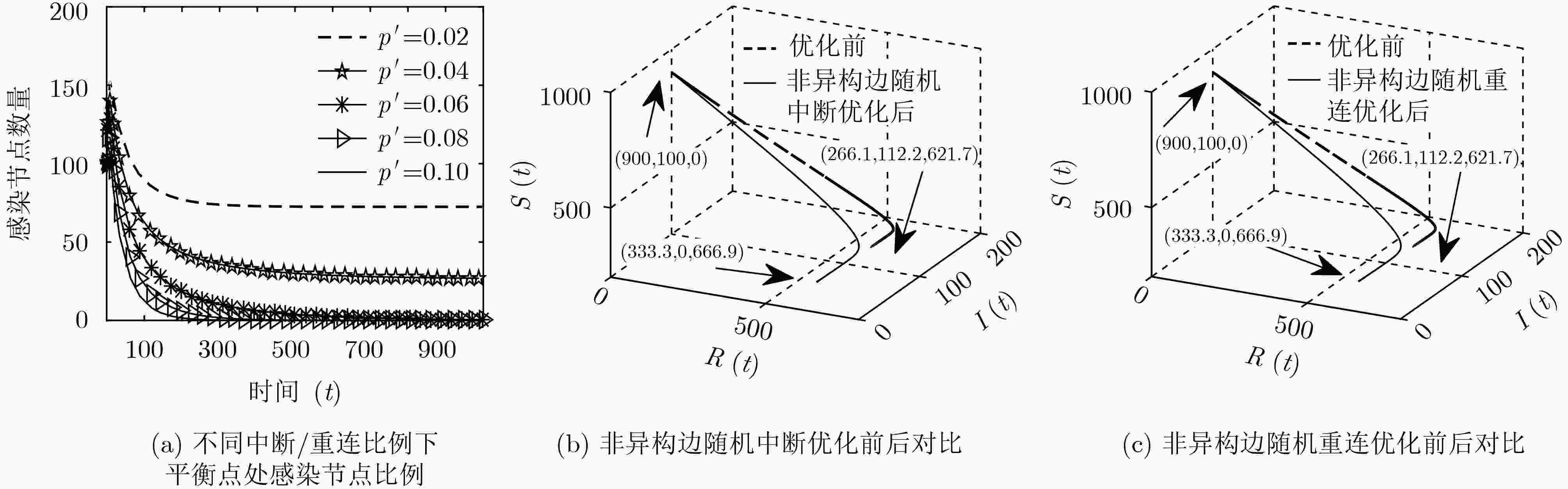
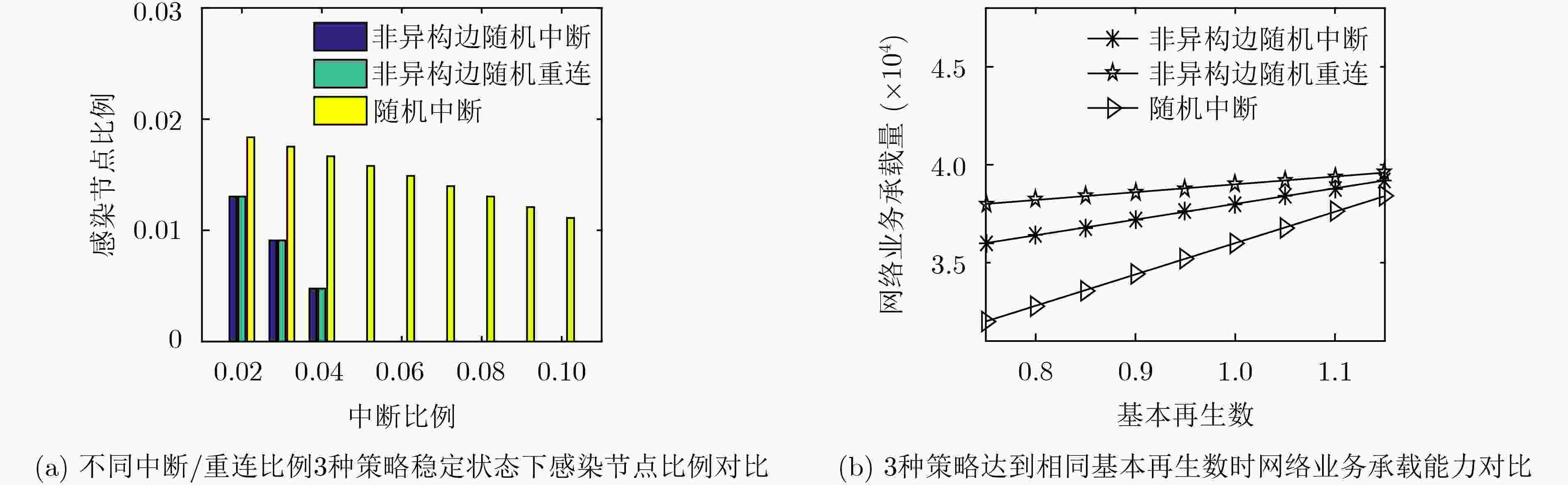
针对蠕虫病毒通常只能感染特定操作系统的特点,该文研究了多操作系统异构网络中的病毒传播规律及安全性能优化策略。首先,考虑多数病毒仅限在同种操作系统之间的链路中传播,在SIRS病毒传播模型中引入异构边比例参数,通过系统平衡点求解和基本再生数分析,研究异构边对单系统病毒传播和网络安全性能的影响。其次,按照动态目标防御思想和技术,设计了非异构边随机中断、非异构边随机重连和单操作系统节点随机跳变3种网络安全优化策略,分析了3种策略下异构边比例和基本再生数的变化及其对网络安全性能的影响。最后仿真验证了病毒传播模型的正确性和3种策略的网络安全性能优化效果,同随机中断和随机隔离策略对比,分析其对网络安全性能和网络业务承载能力的影响。
Abstract:In view of the fact that worm viruses can only infect specific operating systems, the virus propagation rule and security performance optimization strategy in multi-operating system heterogeneous network are studied in this paper. First, considering that most viruses can only spread in link between the same operation system, the parameters of heterogeneous edges ratio are introduced into the Susceptible Infected Remove Susceptible (SIRS) virus transmission model, and the influence of heterogeneous edges and network security performance on the single system virus transmission is studied through system equilibrium solution and basic regeneration number analysis. Secondly, according to the moving target defense thought and technology, the network security optimization strategies is designed for non-isomeric random interrupt, non-isomeric random reconnecting and single operating system random node migration, and the variation of the same ratio and the basic number of regenerated numbers in the three strategies and the impact on the safety of the network are anaylrzed. Finally, the correctness of the virus propagation model is verified by simulation, and the network security performance optimization effects of the three strategies are analyzed.
-
表 1 非异构边随机中断表
输入:初始网络G,断开边的比例${p_{\rm{d}}}$; 输出:优化后的网络${{G}}'$; (1) 为网络中的边加权,其中异构边权重为1,非异构边权重为2; (2) 采用Prime表以网络中度最大的节点为起点生成网络G的最
小生成树G1及其子图G2;(3) 随机删除G2中数量为${p_{\rm{d}}}({M_1} + {M_2})$的连接相应操作系统的边; (4) 将G1和G2整合得到优化后的网络${{G}}'$。 表 2 非异构边随机重连表
输入:初始网络G,重连边的比例${p_{\rm{d}}}$; 输出:优化后的网络${{G}}'$; (1) 为网络中的边加权,其中异构边权重为1,非异构边权重为2; (2) 采用Prime表以网络中度最大节点为起点生成网络G的最小
生成树G1及其补图G2;(3) 随机删除G2中数量为${p_{\rm{d}}}({M_1} + {M_2})$的连接相应操作系统的边; (4) 在网络G2中增添数量为${p_{\rm{d}}}({M_1} + {M_2})$的边,用于连接网络中
不同操作系统类型的节点;(5) 将G1和G2整合得到优化后的网络${{G}}'$。 表 3 单操作系统节点随机跳变算法
输入:初始网络G,目标比例${p_j}$; 输出:优化后的网络G; (1) 随机选取网络中的相应操作系统节点Ni,改变其操作系统类型; (2) 统计网络中相应操作系统比例${p_1}$,若${p_1} < {p_j}$,则进行步骤(3),
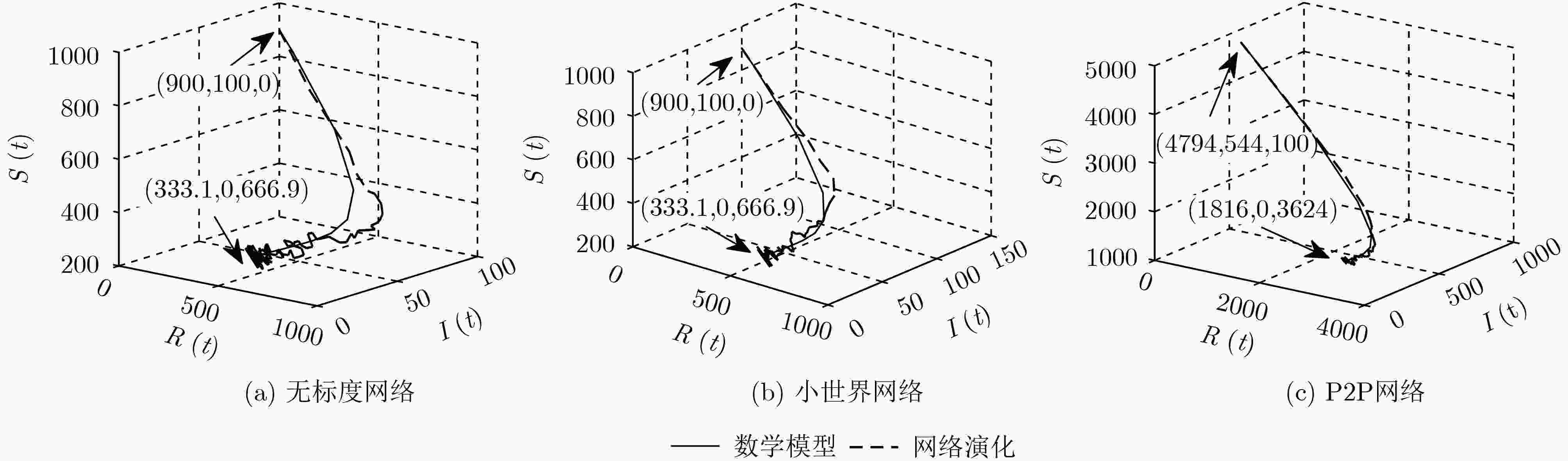
否则重复步骤(1)、步骤(2);(3) 输出网络G。 表 4 数学模型及网络演化结果对比
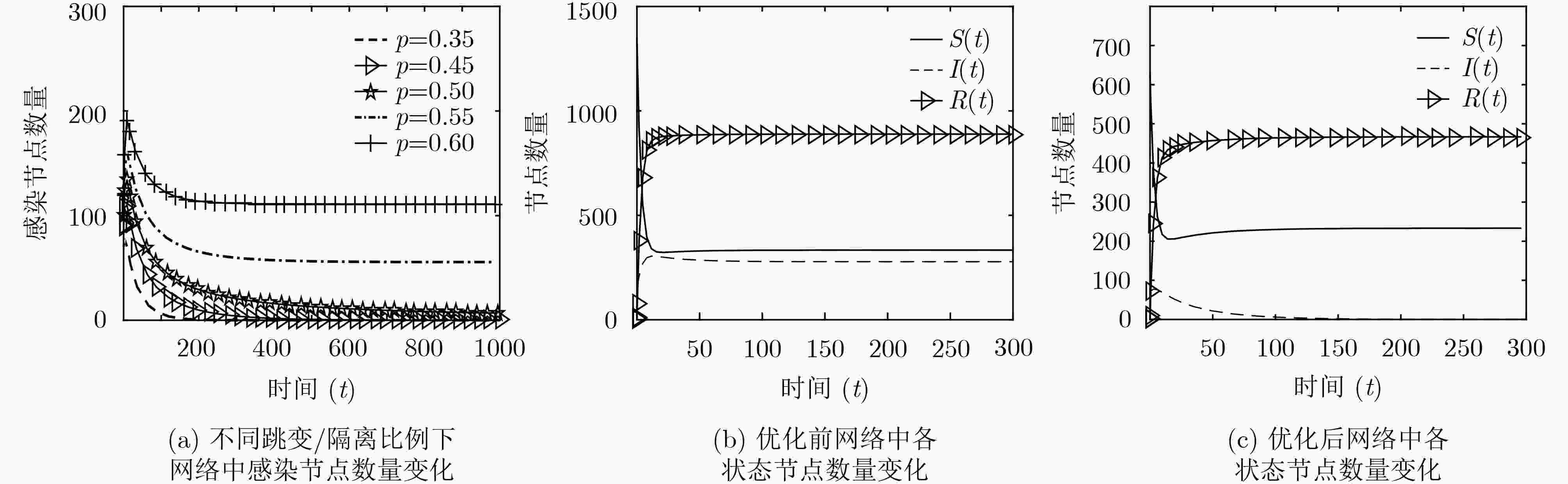
数学模型平衡点位置 网络演化稳态均值 方差 无标度网络 ${P_0}(333.1,0,666.9)$ 337.1,0,662.9 18.10,0,18.10 小世界网络 ${P_0}(333.1,0,666.9)$ 332.9,0,667.1 14.50,0,14.50 P2P网络 ${P_0}(1816,0,3624)$ 1834.1,0,3603.9 22.41,0,22.40 -
PEI Yongzhen, LIU Shaoying, LI Changguo, et al. The dynamics of an impulsive delay SI model with variable coefficients[J]. Applied Mathematical Modelling, 2009, 33(6): 2766–2776. doi: 10.1016/j.apm.2008.08.011 VAN MIEGHEM P. Epidemic phase transition of the SIS type in networks[J]. Europhysics Letters, 2012, 97(4): 48004. doi: 10.1209/0295-5075/97/48004 MARTINEZ J S V, LOPEZ G P, GONZALEZ A J, et al. Numerical approaching of SIR epidemic model for propagation of computer worms[J]. IEEE Latin America Transactions, 2015, 13(10): 3452–3460. doi: 10.1109/TLA.2015.7387254 王刚, 胡鑫, 陆世伟. 节点增减机制下的病毒传播模型及稳定性[J]. 电子科技大学学报, 2019, 48(1): 74–79. doi: 10.3969/j.issn.1001-0548.2019.01.013WANG Gang, HU Xin, and LU Shiwei. Virus spreading model and its stability based on the mechanism of node increasing and decreasing[J]. Journal of University of Electronic Science and Technology of China, 2019, 48(1): 74–79. doi: 10.3969/j.issn.1001-0548.2019.01.013 顾海俊, 蒋国平, 夏玲玲. 基于状态概率转移的SIRS病毒传播模型及其临界值分析[J]. 计算机科学, 2016, 43(6A): 64–67. doi: 10.11896/j.issn.1002-137X.2016.6A.014GU Haijun, JIANG Guoping, and XIA Lingling. SIRS epidemic model and its threshold based on state transition probability[J]. Computer Science, 2016, 43(6A): 64–67. doi: 10.11896/j.issn.1002-137X.2016.6A.014 王刚, 陆世伟, 胡鑫, 等. “去二存一”混合机制下的病毒扩散模型及稳定性分析[J]. 电子与信息学报, 2019, 41(3): 709–716. doi: 10.11999/JEIT180381WANG Gang, LU Shiwei, HU Xin, et al. Virus propagation model and stability under the hybrid mechanism of “Two-go and One-live”[J]. Journal of Electronics &Information Technology, 2019, 41(3): 709–716. doi: 10.11999/JEIT180381 王刚, 陆世伟, 胡鑫, 等. 潜伏机制下网络病毒传播SEIQRS模型及稳定性分析[J]. 哈尔滨工业大学学报, 2019, 51(5): 131–137. doi: 10.11918/j.issn.0367-6234.201805136WANG Gang, LU Shiwei, HU Xin, et al. Network virus spreading SEIQRS model and its stability under escape mechanism[J]. Journal of Harbin Institute of Technology, 2019, 51(5): 131–137. doi: 10.11918/j.issn.0367-6234.201805136 EL-SAYED A M A, ARAFA A A M, KHALI M, et al. A mathematical model with memory for propagation of computer virus under human intervention[J]. Progress in Fractional Differentiation and Applications, 2016, 2(2): 105–113. doi: 10.18576/pfda/020203 WANG Lei, YAO Changhua, YANG Yuqi, et al. Research on a dynamic virus propagation model to improve smart campus security[J]. IEEE Access, 2018, 6: 20663–20672. doi: 10.1109/ACCESS.2018.2817508 HEYDARI V, KIM S I, and YOO S M. Scalable anti-censorship framework using moving target defense for web servers[J]. IEEE Transactions on Information Forensics and Security, 2017, 12(5): 1113–1124. doi: 10.1109/TIFS.2016.2647218 LEI Cheng, MA Duohe, and ZHANG Hongqi. Optimal strategy selection for moving target defense based on Markov game[J]. IEEE Access, 2017, 5: 156–169. doi: 10.1109/ACCESS.2016.2633983 熊鑫立, 赵光胜, 徐伟光, 等. 基于系统攻击面的动态目标防御有效性评估方法[J]. 清华大学学报: 自然科学版, 2019, 59(4): 276–283. doi: 10.16511/j.cnki.qhdxxb.2018.26.056XIONG Xinli, ZHAO Guangsheng, XU Weiguang, et al. System attack surface based MTD effectiveness assessment model[J]. Journal of Tsinghua University:Science and Technology, 2019, 59(4): 276–283. doi: 10.16511/j.cnki.qhdxxb.2018.26.056 周余阳, 程光, 郭春生, 等. 移动目标防御的攻击面动态转移技术研究综述[J]. 软件学报, 2018, 29(9): 2799–2820. doi: 10.13328/j.cnki.jos.005597ZHOU Yuyang, CHENG Guang, GUO Chunsheng, et al. Survey on attack surface dynamic transfer technology based on moving target defense[J]. Journal of Software, 2018, 29(9): 2799–2820. doi: 10.13328/j.cnki.jos.005597 刘江, 张红旗, 杨英杰, 等. 基于主机安全状态迁移模型的动态网络防御有效性评估[J]. 电子与信息学报, 2017, 39(3): 509–517. doi: 10.11999/JEIT160513LIU Jiang, ZHANG Hongqi, YANG Yingjie, et al. Effectiveness evaluation of moving network defense based on host security state transition model[J]. Journal of Electronics &Information Technology, 2017, 39(3): 509–517. doi: 10.11999/JEIT160513 HONG J B and KIM D S. Assessing the effectiveness of moving target defenses using security models[J]. IEEE Transactions on Dependable and Secure Computing, 2016, 13(2): 163–177. doi: 10.1109/TDSC.2015.2443790 JIANG Jiaojiao, WEN Sheng, YU Shui, et al. K-center: An approach on the multi-source identification of information diffusion[J]. IEEE Transactions on Information Forensics and Security, 2015, 10(12): 2616–2626. doi: 10.1109/TIFS.2015.2469256 CAI Jun, WANG Yu, LIU Yan, et al. Enhancing network capacity by weakening community structure in scale-free network[J]. Future Generation Computer Systems, 2018, 87: 765–771. doi: 10.1016/j.future.2017.08.014 LESKOVEC J, KLEINBERG J, and KREVL A. SNAP Datasets: Stanford Large Network Dataset Collection[EB/OL]. http://snap.stanford.edu/data/p2p-Gnutella04.html, 2004. -






 下载:
下载:


 下载:
下载:
