Synthesis of Sparse Rectangular Planar Arrays with Multiple Constraints Based on Dynamic Parameters Differential Evolution Algorithm
-
摘要:
针对多约束条件下稀布矩形平面阵列天线的优化问题,该文提出一种基于动态参数差分进化(DPDE)算法的方向图综合方法。首先,对差分进化(DE)算法中的缩放因子和交叉概率引入动态变化控制策略,提高搜索效率和搜索精度。其次,改进矩阵映射方法,重新定义映射法则,改善现有方法随机性强和搜索精度低的不足。最后,为检验所提方法的有效性进行仿真实验,实验数据表明,该方法可以提高天线优化性能,有效降低天线的峰值旁瓣电平。
Abstract:For solving the problem of the synthesis of sparse rectangular planar arrays with multiple constraints, this paper proposes a Dynamic Parameters Differential Evolution (DPDE) based algorithm. Firstly, to improve searching efficiency and accuracy of Differential Evolution (DE), the proposed method introduces dynamically changing strategies to the scaling factor and the crossover probability of the traditional Differential Evolution algorithm. Secondly, a modified matrix mapping method and the redefinition of mapping principles are presented to make up the defects of strong randomness and low accuracy in existing methods. Finally, simulation experiments of antenna arrays are performed to validate the effectiveness of the proposed method, and the results demonstrate that the proposed method performs out the existing methods in the respect of reducing peak sidelobe level of antenna arrays.
-
表 1 标准测试函数
函数 变量取值范围 最小值 f1 $\displaystyle\sum\limits_{i = 1}^n {x_i^2} $ [–100, 100] 0 f2 $\displaystyle\sum\limits_{i = 1}^n {\left| {{x_i}} \right|} + \prod\limits_{i = 1}^n {{x_i}} $ [–10, 10] 0 f3 ${\displaystyle\sum\limits_{i = 1}^n {\left( {\displaystyle\sum\limits_{j = 1}^i {{x_j}} } \right)} ^2}$ [–100, 100] 0 f4 $\displaystyle\sum\limits_{i = 1}^D {{{\left( {\left| {{x_i} + 0.5} \right|} \right)}^2}\quad } $ [–100, 100] 0 f5 $\displaystyle\sum\limits_{i = 1}^D {\left[ {x_i^2 - 10\cos \left( {2\pi {x_i}} \right) + 10} \right]} $ [–5.12,5.12] 0 f6 $ - 20{ {\rm{e} }^{ - 0.2\sqrt {\dfrac{1}{D}\displaystyle\sum\limits_{i = 1}^D {x_i^2} } } } - { {\rm{e} }^{\dfrac{1}{D}\displaystyle\sum\limits_{i = 1}^D {\cos \left( {2\pi {x_i} } \right)} } } + 20 + {\rm{e} }$ [–32, 32] 0 f7 $\dfrac{1}{ {400} }\displaystyle\sum\limits_{i = 1}^D {x_i^2} - \prod\limits_{i = 1}^D {\cos \left( {\frac{ { {x_i} } }{ {\sqrt i } } } \right)} + 1$ [–600, 600] 0 表 2 实验参数设置
缩放因子 交叉概率Cr 种群规模NP 迭代次数NI 变量维度D 缩放因子F 变异概率Mr DPDE $1/\sqrt t $ 自适应 50 10000 100/200 0.5 0.5 DE (无) 0.5 表 3 DPDE和DE的实验结果对比(较好的以*标出)
DPDE (D=100) DE (D=100) DPDE (D=200) DE (D=200) MEAN SD PSR(%) MEAN SD PSR(%) MEAN SD PSR(%) MEAN SD PSR(%) f1 2.72E-28* 5.23E-56 100 1.86E-14 5.94E-29 100 5.16E-17* 6.17E-34 100 1.87E+01 7.91E+00 0 f2 1.87E-14* 5.83E-29 100 7.97E-09 2.65E-18 0 1.01E-08* 9.34E-18 0 4.73E+00 3.23E-01 0 f3 1.41E+00* 3.61E-02 0 3.39E+05 5.07E+08 0 9.04E+00* 1.32E+00 0 1.33E+06 1.02E+10 0 f4 9.25E-28* 9.62E-55 100 1.99E-14 6.35E-29 100 1.97E-16* 1.01E-32 100 1.92E+01 1.12E+01 0 f5 3.72E+01* 1.77E+02 0 7.67E+02 3.69E+02 0 2.11E+02* 2.14E+03 0 2.04E+03 8.78E+02 0 f6 1.54E-14* 3.52E-30 100 2.80E-08 3.13E-17 0 1.68E-09* 2.27E-19 0 2.05E+00 9.44E-01 0 f7 8.66E-17* 2.16E-33 100 1.08E-14 1.55E-29 100 2.33E-16* 1.64E-33 100 2.74E+00 1.12E-01 0 表 4 仿真实验结果对比(dB)
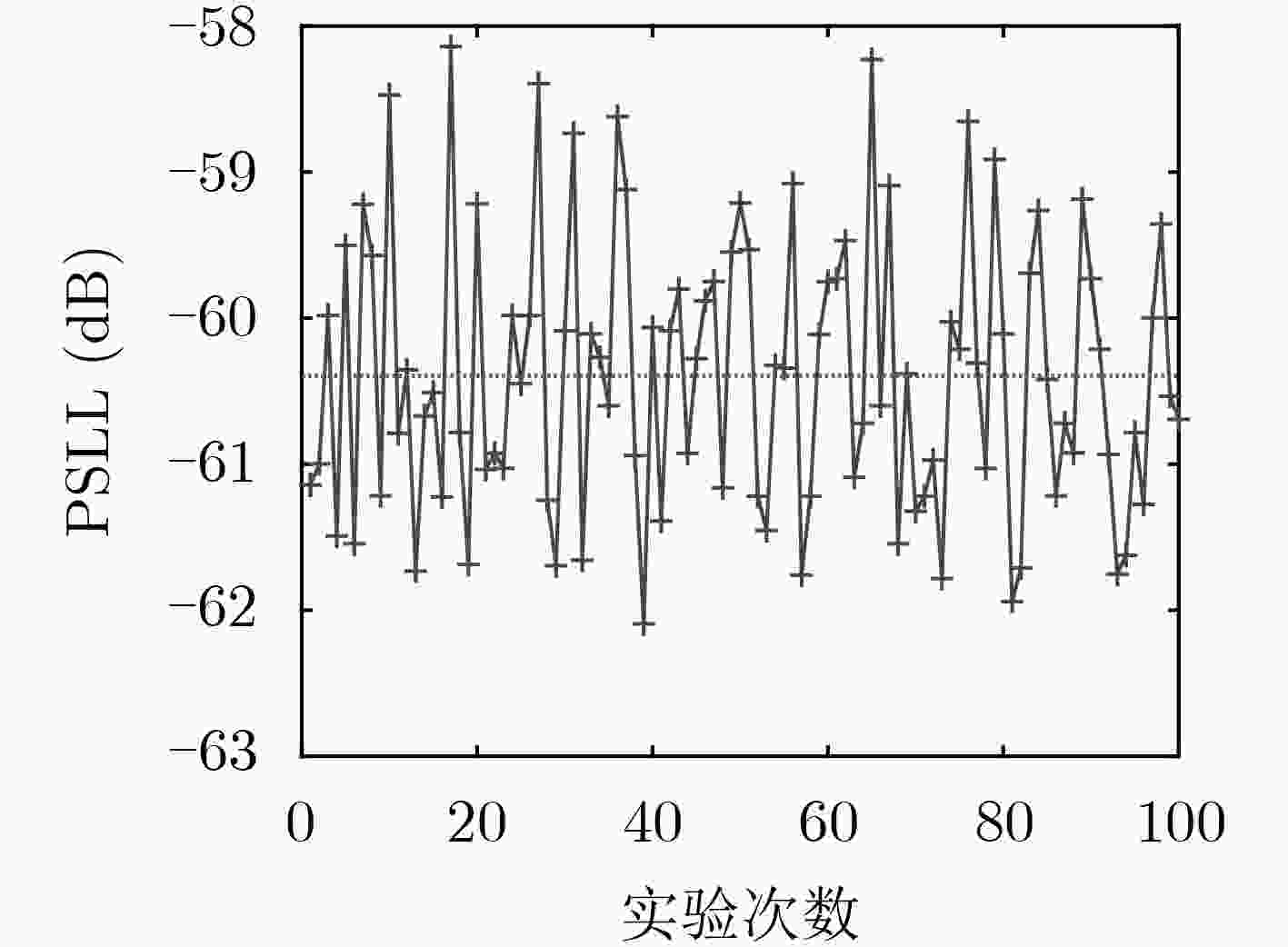
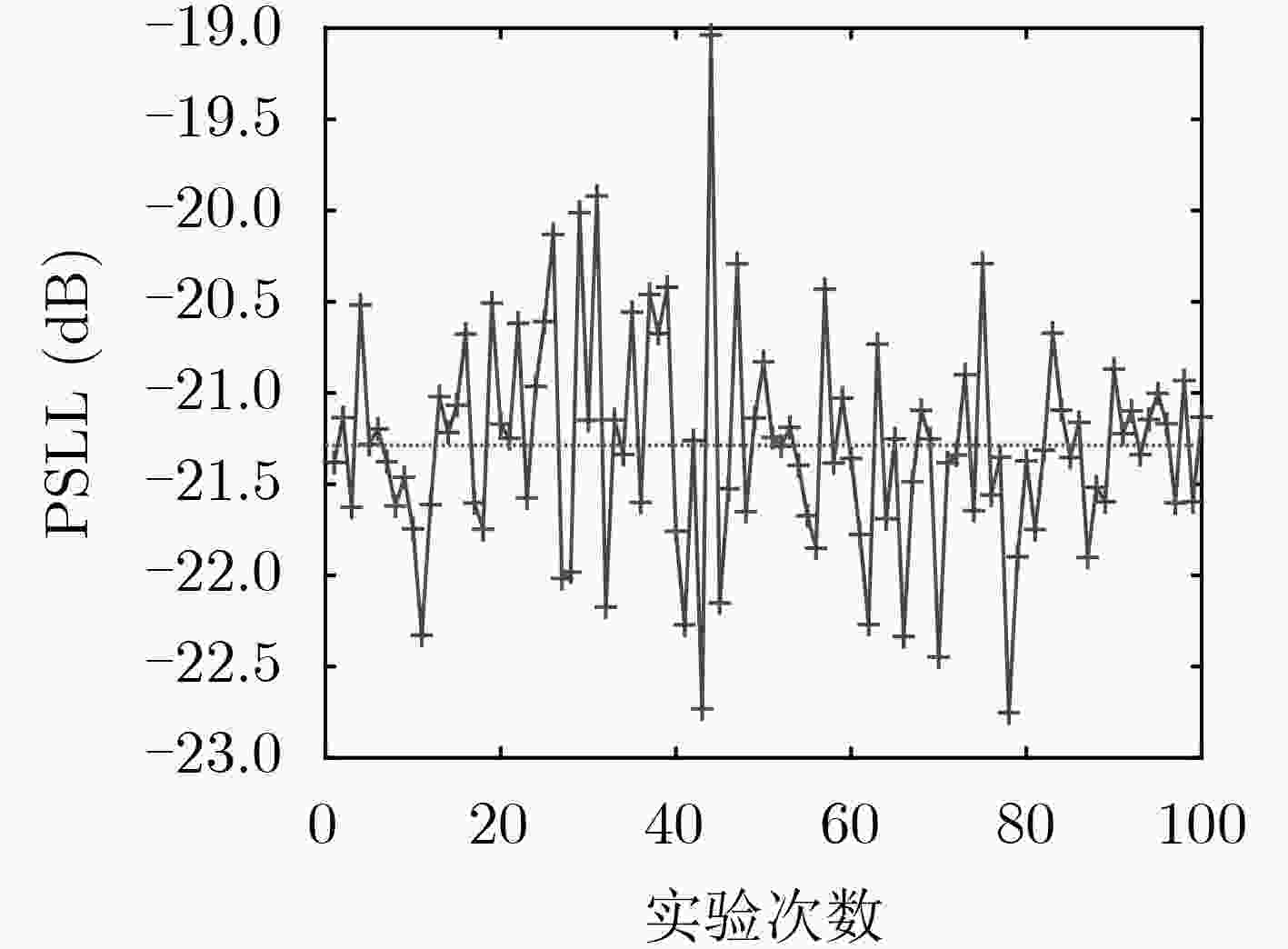
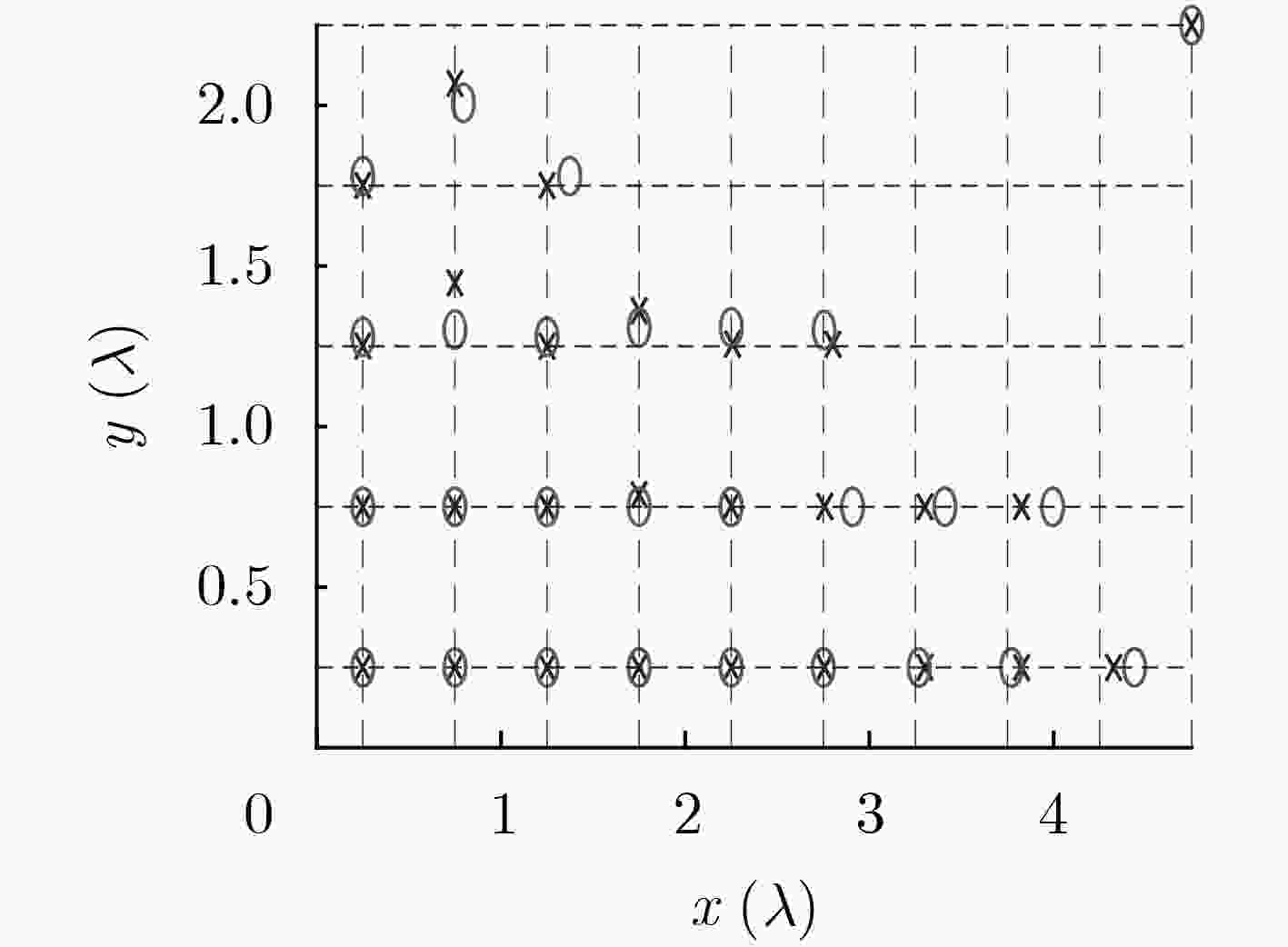
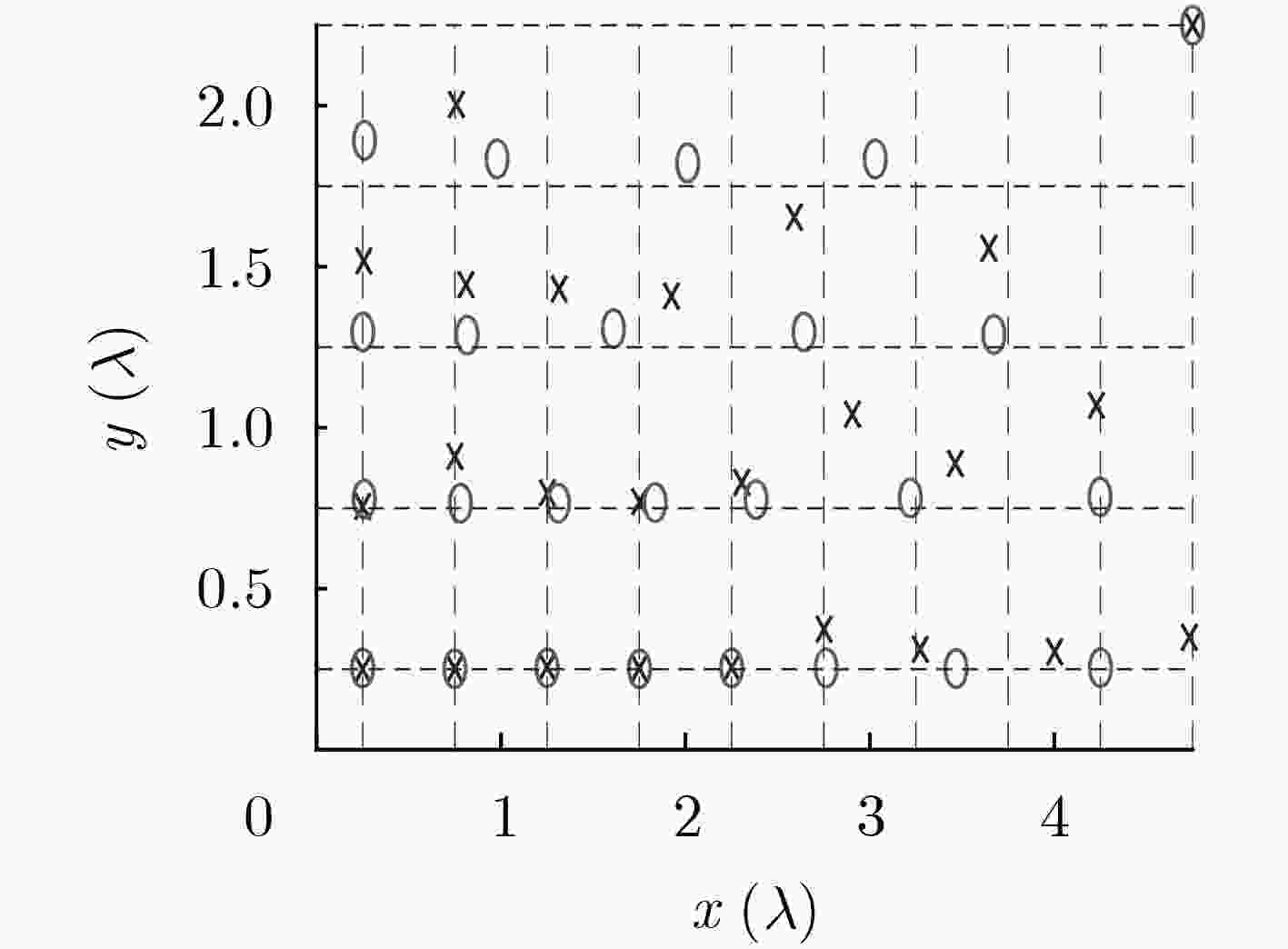
实验 方法 最优值 均值 最差值 方差 实验1 本文方法 –62.093 –60.395 –58.141 0.898 MGA –45.456 – –43.864 – MMM –51.499 – –49.269 – AMM –61.454 –58.922 – – 实验2 本文方法 –22.753 –21.287 –19.038 0.363 MGA –18.840 – – – MMM –20.384 – – – AMM –21.886 –20.456 – – -
OLIVERI G and MASSA A. Genetic algorithm (GA)-enhanced almost difference set (ADS)-based approach for array thinning[J]. IET Microwaves, Antennas & Propagation, 2011, 5(3): 305–315. doi: 10.1049/iet-map.2010.0114 CHEN Kesong, CHEN Hui, WANG Ling, et al. Modified real GA for the synthesis of sparse planar circular arrays[J]. IEEE Antennas and Wireless Propagation Letters, 2016, 15: 274–277. doi: 10.1109/LAWP.2015.2440432 BHATTACHARYA R, BHATTACHARYYA T K, and GARG R. Position mutated hierarchical particle swarm optimization and its application in synthesis of unequally spaced antenna arrays[J]. IEEE Transactions on Antennas and Propagation, 2012, 60(7): 3174–3181. doi: 10.1109/tap.2012.2196917 DAI Dingcheng, YAO Minli, MA Hongguang, et al. An effective approach for the synthesis of uniformly excited large linear sparse array[J]. IEEE Antennas and Wireless Propagation Letters, 2018, 17(3): 377–380. doi: 10.1109/LAWP.2018.2790907 BAI Yanying, XIAO Shaoqiu, LIU Changrong, et al. A hybrid IWO/PSO algorithm for pattern synthesis of conformal phased arrays[J]. IEEE Transactions on Antennas and Propagation, 2013, 61(4): 2328–2332. doi: 10.1109/tap.2012.2231936 SUN Geng, LIU Yanheng, CHEN Zhaoyu, et al. Radiation beam pattern synthesis of concentric circular antenna arrays using hybrid approach based on cuckoo search[J]. IEEE Transactions on Antennas and Propagation, 2018, 66(9): 4563–4576. doi: 10.1109/TAP.2018.2846771 ZHANG Bo, LIU Wei, and GOU Xiaoming. Compressive sensing based sparse antenna array design for directional modulation[J]. IET Microwaves, Antennas & Propagation, 2017, 11(5): 634–641. doi: 10.1049/iet-map.2016.0313 YAN Chuang, YANG Peng, XING Zhiyu, et al. Synthesis of planar sparse arrays with minimum spacing constraint[J]. IEEE Antennas and Wireless Propagation Letters, 2018, 17(6): 1095–1098. doi: 10.1109/LAWP.2018.2833962 GU Pengfei, WANG Gui, FAN Zhenhong, et al. Efficient unitary matrix pencil method for synthesising wideband frequency patterns of sparse linear arrays[J]. IET Microwaves, Antennas & Propagation, 2018, 12(12): 1871–1876. doi: 10.1049/iet-map.2018.0148 LIN Zhiqiang, JIA Weimin, YAO Minli, et al. Synthesis of sparse linear arrays using vector mapping and simultaneous perturbation stochastic approximation[J]. IEEE Antennas and Wireless Propagation Letters, 2012, 11: 220–223. doi: 10.1109/LAWP.2012.2188266 贾维敏, 林志强, 姚敏立, 等. 一种多约束稀布线阵的天线综合方法[J]. 电子学报, 2013, 41(5): 926–930. doi: 10.3969/j.issn.0372-2112.2013.05.015JIA Weimin, LIN Zhiqiang, YAO Minli, et al. A synthesis technique for linear sparse arrays with multiple constraints[J]. Acta Electronica Sinica, 2013, 41(5): 926–930. doi: 10.3969/j.issn.0372-2112.2013.05.015 于波, 陈客松, 朱盼, 等. 稀布圆阵的降维优化方法[J]. 电子与信息学报, 2014, 36(2): 476–481. doi: 10.3724/SP.J.1146.2013.00526YU Bo, CHEN Kesong, ZHU Pan, et al. An optimum method of sparse concentric rings array based on dimensionality reduction[J]. Journal of Electronics &Information Technology, 2014, 36(2): 476–481. doi: 10.3724/SP.J.1146.2013.00526 CHEN Kesong, YUN Xiaohua, HE Zishu, et al. Synthesis of sparse planar arrays using modified real genetic algorithm[J]. IEEE Transactions on Antennas and Propagation, 2007, 55(4): 1067–1073. doi: 10.1109/tap.2007.893375 LIU Heng, ZHAO Hongwei, LI Weimei, et al. Synthesis of sparse planar arrays using matrix mapping and differential evolution[J]. IEEE Antennas and Wireless Propagation Letters, 2016, 15: 1905–1908. doi: 10.1109/LAWP.2016.2542882 DAI Dingcheng, YAO Minli, MA Hongguang, et al. An asymmetric mapping method for the synthesis of sparse planar arrays[J]. IEEE Antennas and Wireless Propagation Letters, 2018, 17(1): 70–73. doi: 10.1109/LAWP.2017.2774498 LI Xiangtao, WANG Jianan, and YIN Minghao. Enhancing the performance of cuckoo search algorithm using orthogonal learning method[J]. Neural Computing and Applications, 2014, 24(6): 1233–1247. doi: 10.1007/s00521-013-1354-6 -





 下载:
下载:




 下载:
下载:
