Group-Label-Specific Features Learning Based on Label-Density Classification Margin
-
摘要:
类属属性学习避免相同属性预测全部标记,是一种提取各标记独有属性进行分类的一种框架,在多标记学习中得到广泛的应用。而针对标记维度较大、标记分布密度不平衡等问题,已有的基于类属属性的多标记学习算法普遍时间消耗大、分类精度低。为提高多标记分类性能,该文提出一种基于标记密度分类间隔面的组类属属性学习(GLSFL-LDCM)方法。首先,使用余弦相似度构建标记相关性矩阵,通过谱聚类将标记分组以提取各标记组的类属属性,减少计算全部标记类属属性的时间消耗。然后,计算各标记密度以更新标记空间矩阵,将标记密度信息加入原标记中,扩大正负标记的间隔,通过标记密度分类间隔面的方法有效解决标记分布密度不平衡问题。最后,通过将组类属属性和标记密度矩阵输入极限学习机以得到最终分类模型。对比实验充分验证了该文所提算法的可行性与稳定性。
Abstract:The label-specific features learning avoids the same features prediction for all class labels, it is a kind of framework for extracting the specific features of each label for classification, so it is widely used in multi-label learning. For the problems of large label dimension and unbalanced label distribution density, the existing multi-label learning algorithm based on label-specific features has larger time consumption and lower classification accuracy. In order to improve the performance of classification, a Group-Label-Specific Features Learning method based on Label-Density Classification Margin (GLSFL-LDCM) is proposed. Firstly, the cosine similarity is used to construct the label correlation matrix, and the class labels are grouped by spectral clustering to extract the label-specific features of each label group to reduce the time consumption for calculating the label-specific features of all class labels. Then, the density of each label is calculated to update the label space matrix, the label-density information is added to the original label space. The classification margin between the positive and negative labels is expanded, thus the imbalance label distribution density problem is effectively solved by the method of label-density classification margin. Finally, the final classification model is obtained by inputting the group-label-specific features and the label-density matrix into the extreme learning machine. The comparison experiment results verify fully the feasibility and stability of the proposed algorithm.
-
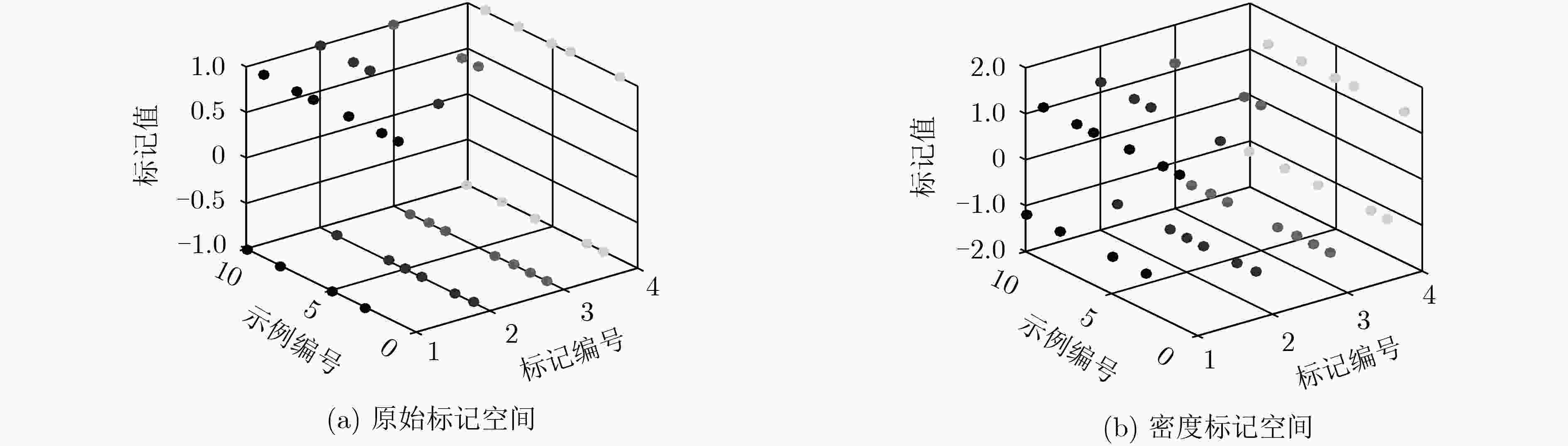
表 1 标记空间虚拟数据集
标记编号 原标记 密度标记 Y1 Y2 Y3 Y4 Y1 Y2 Y3 Y4 1 +1 –1 –1 +1 +1.333 –1.273 –1.318 +1.278 2 +1 –1 –1 –1 +1.333 –1.273 –1.318 –1.227 3 –1 +1 –1 –1 –1.182 +1.222 –1.318 –1.227 4 +1 –1 –1 +1 +1.333 –1.273 –1.318 +1.278 5 –1 –1 +1 +1 –1.182 –1.273 +1.167 +1.278 6 +1 –1 +1 –1 +1.333 –1.273 +1.167 –1.227 7 +1 +1 –1 +1 +1.333 +1.222 –1.318 +1.278 8 –1 +1 –1 –1 –1.182 +1.222 –1.318 –1.227 9 +1 –1 –1 +1 +1.333 –1.273 –1.318 +1.278 10 –1 +1 +1 –1 –1.182 +1.222 +1.167 –1.227 表 2 GLSFL-LDCM算法步骤
输入:训练数据集$D = \left\{ {{{{x}}_i},{{{Y}}_i}} \right\}_{i = 1}^N$,测试数据集
${D^*} = \left\{ {{{x}}_j^*} \right\}_{j = 1}^{{N^*}}$,RBF核参数γ,惩罚因子C,类属属性参数:
α, β, μ,聚类数K;输出:预测标记Y*. Training: training data set D (1) 用式(1)、式(2)计算余弦相似度,构造标记相关性矩阵LC (2) 用式(3)谱聚类将标记分组:G=[G1,G2, ···, GK] (3) 用式(5)、式(6)构建类属属性提取矩阵S (4) 通过式(7)、式(8)更新标记空间,构造标记密度矩阵:YD (5) For k = 1, 2, ···, K do ${{\varOmega}} _{{\rm{ELM}}}^k = {{{\varOmega}} _{{\rm{ELM}}}}({{x}}(:,{{{S}}^k} \ne 0))$ ${\bf{YD}}{^k} = {\bf{YD}}({{{G}}_k})$ ${ {{\beta} } ^k} = {\left(\dfrac{ {{I} } }{C} + {{\varOmega} } _{ {\rm{ELM} } }^k\right)^{ - 1} }{\bf{YD} }{^k}$ Prediction: testing data set D* (a) For k = 1, 2, ···, K do ${{G}}_k^* = {{{\varOmega}} _{{\rm{ELM}}}}({{{x}}^*}(:,{{{S}}^k} \ne 0)){{{\beta}} ^k}$ (b) ${{{Y}}^*} = \left[ {{{G}}_1^*,{{G}}_2^*,...,{{G}}_K^*} \right]$ 表 3 多标记数据描述
数据集 样本数 特征数 标记数 标记基数 应用领域 Emotions1) 593 72 6 1.869 MUSIC Genbase1) 662 1186 27 1.252 BIOLOGY Medical1) 978 1449 45 1.245 TEXT Enron3) 1702 1001 53 4.275 TEXT Image2) 2000 294 5 1.236 IMAGE Scene1) 2407 294 6 1.074 IMAGE Yeast1) 2417 103 14 4.237 BIOLOGY Slashdot3) 3782 1079 22 0.901 TEXT 表 4 对比算法实验结果
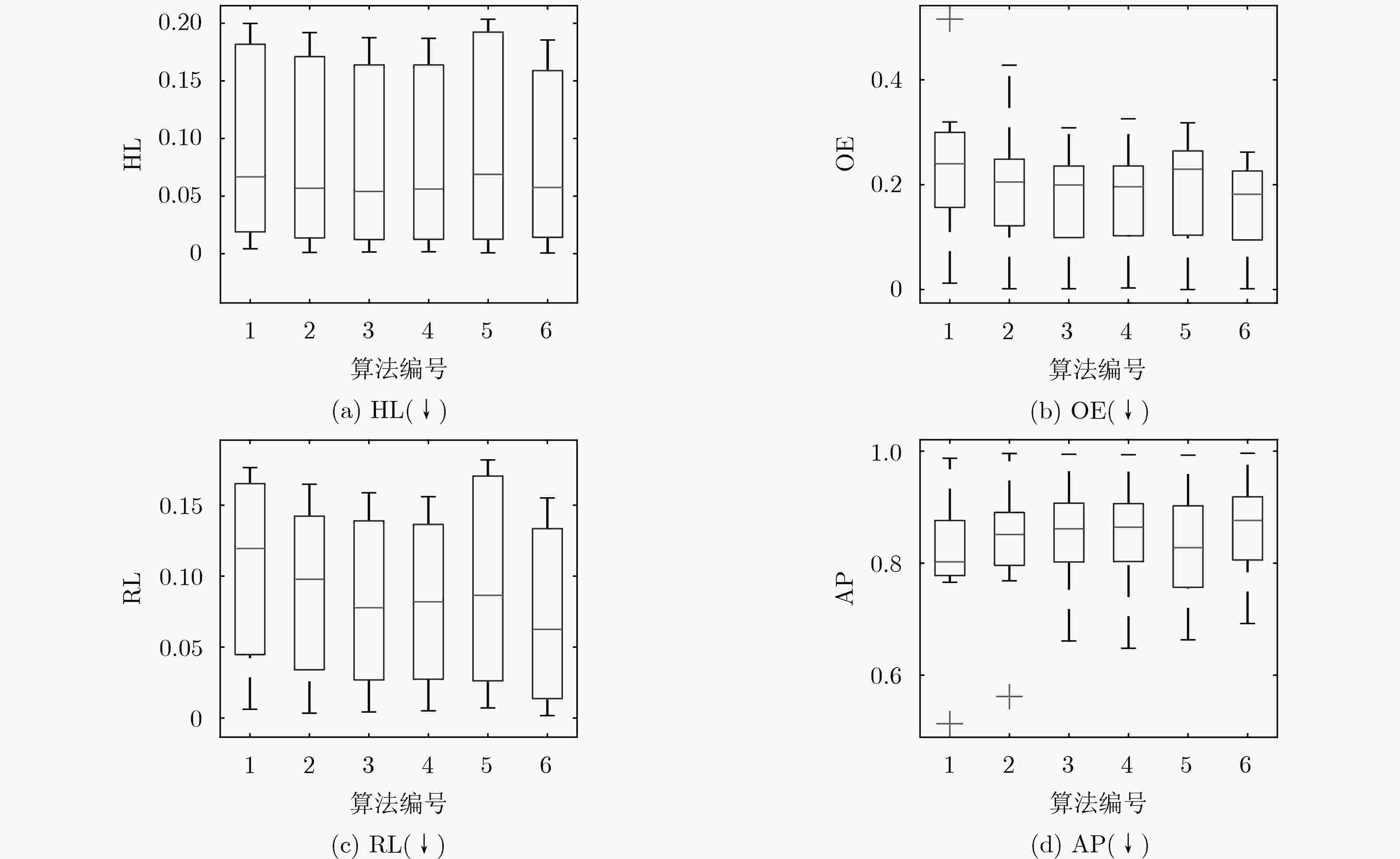
数据集 ML-kNN LIFT FRS-LIFT FRS-SS-LIFT LLSF-DL GLSFL-LDCM HL↓ Emotions 0.1998±0.0167● 0.1854±0.0260● 0.1798±0.0290● 0.1809±0.0310● 0.2035±0.0082● 0.1782±0.0154 Genbase 0.0043±0.0017● 0.0011±0.0016● 0.0015±0.0009● 0.0017±0.0011● 0.0008±0.0014● 0.0006±0.0005 Medical 0.0158±0.0015● 0.0115±0.0013● 0.0087±0.0014○ 0.0089±0.0013 0.0092±0.0004 0.0089±0.0021 Enron 0.0482±0.0043● 0.0365±0.0034○ 0.0341±0.0032○ 0.0372±0.0034○ 0.0369±0.0034○ 0.0468±0.0021 Image 0.1701±0.0141● 0.1567±0.0136● 0.1479±0.0103● 0.1468±0.0097● 0.1828±0.0152● 0.1397±0.0133 Scene 0.0852±0.0060● 0.0772±0.0047● 0.0740±0.0052● 0.0751±0.0057● 0.1008±0.0059● 0.0682±0.0084 Yeast 0.1934±0.0116● 0.1919±0.0083● 0.1875±0.0114● 0.1869±0.0111● 0.2019±0.0060● 0.1855±0.0079 Slashdot 0.0221±0.0010● 0.0159±0.0009○ 0.0159±0.0011○ 0.0160±0.0011○ 0.0158±0.0012○ 0.0196±0.0010 win/tie/loss 8/0/0 6/0/2 5/0/3 5/1/2 5/1/2 – 数据集 ML-kNN LIFT FRS-LIFT FRS-SS-LIFT LLSF-DL GLSFL-LDCM OE↓ Emotions 0.2798±0.0441● 0.2291±0.0645● 0.2155±0.0608 0.2223±0.0651● 0.2583±0.0201● 0.2157±0.0507 Genbase 0.0121±0.0139● 0.0015±0.0047 0.0015±0.0047 0.0030±0.0094● 0.0000±0.0000○ 0.0015±0.0048 Medical 0.2546±0.0262● 0.1535±0.0258● 0.1124±0.0279○ 0.1186±0.0231○ 0.1285±0.0271● 0.1226±0.0383 Enron 0.5158±0.0417● 0.4279±0.0456● 0.3084±0.0444● 0.3256±0.0437● 0.2704±0.0321● 0.2221±0.0227 Image 0.3195±0.0332● 0.2680±0.0256● 0.2555±0.0334● 0.2490±0.0226● 0.3180±0.0326● 0.2365±0.0224 Scene 0.2185±0.0313● 0.1924±0.0136● 0.1841±0.0156● 0.1836±0.0195● 0.2323±0.0267● 0.1562±0.0316 Yeast 0.2251±0.0284● 0.2177±0.0255● 0.2147±0.0171● 0.2085±0.0156● 0.2267±0.0239● 0.2072±0.0250 Slashdot 0.0946±0.0143● 0.0898±0.0134● 0.0858±0.0162○ 0.0864±0.0138○ 0.0887±0.0123● 0.0874±0.0107 win/tie/loss 8/0/0 7/1/0 4/2/2 6/0/2 7/0/1 – 数据集 ML-kNN LIFT FRS-LIFT FRS-SS-LIFT LLSF-DL GLSFL-LDCM RL↓ Emotions 0.1629±0.0177● 0.1421±0.0244● 0.1401±0.0299● 0.1406±0.0280● 0.1819±0.0166● 0.1375±0.0226 Genbase 0.0062±0.0082● 0.0034±0.0065● 0.0043±0.0071● 0.0051±0.0077● 0.0071±0.0031● 0.0017±0.0025 Medical 0.0397±0.0093● 0.0262±0.0072● 0.0248±0.0108● 0.0236±0.0074● 0.0218±0.0080● 0.0148±0.0096 Enron 0.1638±0.0222● 0.1352±0.0190● 0.0953±0.0107● 0.1046±0.0099● 0.0927±0.0069● 0.0735±0.0084 Image 0.1765±0.0202● 0.1425±0.0169● 0.1378±0.0149● 0.1323±0.0171● 0.1695±0.0162● 0.1294±0.0127 Scene 0.0760±0.0100● 0.0604±0.0047● 0.0601±0.0061● 0.0592±0.0072● 0.0803±0.0133● 0.0515±0.0093 Yeast 0.1666±0.0149● 0.1648±0.0121● 0.1588±0.0150● 0.1560±0.0138● 0.1716±0.0145● 0.1551±0.0100 Slashdot 0.0497±0.0072● 0.0418±0.0062● 0.0289±0.0038● 0.0311±0.0038● 0.0307±0.0058● 0.0126±0.0018 win/tie/loss 8/0/0 8/0/0 8/0/0 8/0/0 8/0/0 – 数据集 ML-kNN LIFT FRS-LIFT FRS-SS-LIFT LLSF-DL GLSFL-LDCM AP↑ Emotions 0.7980±0.0254● 0.8236±0.0334● 0.8280±0.0411● 0.8268±0.0400● 0.7504±0.0120● 0.8316±0.0265 Genbase 0.9873±0.0121● 0.9958±0.0078● 0.9944±0.0078● 0.9935±0.0085● 0.9928±0.0024● 0.9962±0.0057 Medical 0.8068±0.0248● 0.8784±0.0145● 0.9096±0.0176● 0.9087±0.0155● 0.9028±0.0172● 0.9122±0.0281 Enron 0.5134±0.0327● 0.5620±0.0321● 0.6611±0.0408● 0.6481±0.0287● 0.6632±0.0182● 0.6923±0.0159 Image 0.7900±0.0203● 0.8240±0.0169● 0.8314±0.0177● 0.8364±0.0162● 0.7943±0.0177● 0.8444±0.0118 Scene 0.8687±0.0164● 0.8884±0.0081● 0.8913±0.0084● 0.8921±0.0101● 0.8609±0.0182● 0.9082±0.0173 Yeast 0.7659±0.0194● 0.7685±0.0148● 0.7762±0.0172● 0.7790±0.0167● 0.7633±0.0160● 0.7798±0.0140 Slashdot 0.8835±0.0116● 0.8927±0.0091● 0.9045±0.0098● 0.9038±0.0074● 0.9017±0.0095● 0.9247±0.0059 win/tie/loss 8/0/0 8/0/0 8/0/0 8/0/0 8/0/0 – 表 5 各算法的时耗对比(s)
数据集 1 2 3 4 5 6 Emotions 0.2 0.4 54.0 8.7 0.1 0.1 Genbase 1.0 2.9 15.0 1.7 0.9 0.2 Medical 4.3 12.5 66.3 14.8 2.3 0.4 Enron 6.5 48.1 1292.7 182.7 0.6 0.6 Image 3.4 8.1 1805.2 320.5 0.1 0.2 Scene 5.4 7.9 2174.1 404.2 0.1 0.2 Yeast 3.5 44.3 13113.4 3297.7 0.2 0.3 Slashdot 34.1 84.5 11895.5 2650.0 1.1 0.8 平均 7.3 26.1 3802.0 860.0 0.7 0.4 表 6 模型分解对比实验
数据集 KELM LSFL-KELM GLSFL-KELM LDCM-KELM HL↓ Emotions 0.1840±0.0275 0.1837±0.0253 0.1824±0.0196 0.1802±0.0295 Genbase 0.0010±0.0008 0.0008±0.0005 0.0006±0.0006 0.0007±0.0006 Medical 0.0094±0.0030 0.0093±0.0017 0.0091±0.0016 0.0092±0.0019 Scene 0.0706±0.0051 0.0693±0.0079 0.0683±0.0059 0.0682±0.0062 数据集 KELM LSFL-KELM GLSFL-KELM LDCM-KELM AP↑ Emotions 0.8144±0.0369 0.8223±0.0252 0.8296±0.0278 0.8306±0.0429 Genbase 0.9926±0.0046 0.9928±0.0048 0.9961±0.0046 0.9956±0.0038 Medical 0.9077±0.0262 0.9092±0.0229 0.9124±0.0205 0.9126±0.0306 Scene 0.9010±0.0127 0.9024±0.0186 0.9059±0.0132 0.9033±0.0152 -
ZHANG Minling and ZHOU Zhihua. ML-KNN: A lazy learning approach to multi-label learning[J]. Pattern Recognition, 2007, 40(7): 2038–2048. doi: 10.1016/j.patcog.2006.12.019 LIU Yang, WEN Kaiwen, GAO Quanxue, et al. SVM based multi-label learning with missing labels for image annotation[J]. Pattern Recognition, 2018, 78: 307–317. doi: 10.1016/j.patcog.2018.01.022 ZHANG Junjie, WU Qi, SHEN Chunhua, et al. Multilabel image classification with regional latent semantic dependencies[J]. IEEE Transactions on Multimedia, 2018, 20(10): 2801–2813. doi: 10.1109/TMM.2018.2812605 AL-SALEMI B, AYOB M, and NOAH S A M. Feature ranking for enhancing boosting-based multi-label text categorization[J]. Expert Systems with Applications, 2018, 113: 531–543. doi: 10.1016/j.eswa.2018.07.024 ZHANG Minling and ZHOU Zhihua. Multilabel neural networks with applications to functional genomics and text categorization[J]. IEEE Transactions on Knowledge and Data Engineering, 2006, 18(10): 1338–1351. doi: 10.1109/TKDE.2006.162 GUAN Renchu, WANG Xu, YANG M Q, et al. Multi-label deep learning for gene function annotation in cancer pathways[J]. Scientific Reports, 2018, 8: No. 267. doi: 10.1038/s41598-017-17842-9 SAMY A E, EL-BELTAGY S R, and HASSANIEN E. A context integrated model for multi-label emotion detection[J]. Procedia Computer Science, 2018, 142: 61–71. doi: 10.1016/j.procs.2018.10.461 ALMEIDA A M G, CERRI R, PARAISO E C, et al. Applying multi-label techniques in emotion identification of short texts[J]. Neurocomputing, 2018, 320: 35–46. doi: 10.1016/j.neucom.2018.08.053 TSOUMAKAS G and KATAKIS I. Multi-label classification: An overview[J]. International Journal of Data Warehousing and Mining, 2007, 3(3): No. 1. doi: 10.4018/jdwm.2007070101 ZHANG Minling and ZHOU Zhihua. A review on multi-label learning algorithms[J]. IEEE Transactions on Knowledge and Data Engineering, 2014, 26(8): 1819–1837. doi: 10.1109/TKDE.2013.39 CRAMMER K, DREDZE M, GANCHEV K, et al. Automatic code assignment to medical text[C]. Workshop on BioNLP 2007: Biological, Translational, and Clinical Language Processing, Stroudsburg, USA, 2007: 129–136. ZHANG Minling and WU Lei. Lift: Multi-label learning with label-specific features[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2015, 37(1): 107–120. doi: 10.1109/TPAMI.2014.2339815 XU Suping, YANG Xibei, YU Hualong, et al. Multi-label learning with label-specific feature reduction[J]. Knowledge-Based Systems, 2016, 104: 52–61. doi: 10.1016/j.knosys.2016.04.012 SUN Lu, KUDO M, and KIMURA K. Multi-label classification with meta-label-specific features[C]. 2016 IEEE International Conference on Pattern Recognition, Cancun, Mexico, 2016: 1612–1617. doi: 10.1109/ICPR.2016.7899867. HUANG Jun, LI Guorong, HUANG Qingming, et al. Joint feature selection and classification for multilabel learning[J]. IEEE Transactions on Cybernetics, 2018, 48(3): 876–889. doi: 10.1109/TCYB.2017.2663838 WENG Wei, LIN Yaojin, WU Shunxiang, et al. Multi-label learning based on label-specific features and local pairwise label correlation[J]. Neurocomputing, 2018, 273: 385–394. doi: 10.1016/j.neucom.2017.07.044 HUANG Jun, LI Guorong, HUANG Qingming, et al. Learning label-specific features and class-dependent labels for multi-label classification[J]. IEEE Transactions on Knowledge and Data Engineering, 2016, 28(12): 3309–3323. doi: 10.1109/TKDE.2016.2608339 HUANG Guangbin, ZHU Qinyu, and SIEW C K. Extreme learning machine: Theory and applications[J]. Neurocomputing, 2006, 70(1/3): 489–501. doi: 10.1016/j.neucom.2005.12.126 HUANG Guangbin, ZHOU Hongming, DING Xiaojian, et al. Extreme learning machine for regression and multiclass classification[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics) , 2012, 42(2): 513–529. doi: 10.1109/TSMCB.2011.2168604 赵小强, 刘晓丽. 基于公理化模糊子集的改进谱聚类算法[J]. 电子与信息学报, 2018, 40(8): 1904–1910. doi: 10.11999/JEIT170904ZHAO Xiaoqiang and LIU Xiaoli. An improved spectral clustering algorithm based on axiomatic fuzzy set[J]. Journal of Electronics &Information Technology, 2018, 40(8): 1904–1910. doi: 10.11999/JEIT170904 BOYD S, PARIKH N, CHU E, et al. Distributed optimization and statistical learning via the alternating direction method of multipliers[J]. Foundations and Trends® in Machine learning, 2010, 3(1): 1–122. doi: 10.1561/2200000016 LIU Xinwang, WANG Lei, HUANG Guangbin, et al. Multiple kernel extreme learning machine[J]. Neurocomputing, 2015, 149: 253–264. doi: 10.1016/j.neucom.2013.09.072 邓万宇, 郑庆华, 陈琳, 等. 神经网络极速学习方法研究[J]. 计算机学报, 2010, 33(2): 279–287. doi: 10.3724/SP.J.1016.2010.00279DENG Wanyu, ZHENG Qinghua, CHEN Lin, et al. Research on extreme learning of neural networks[J]. Chinese Journal of Computers, 2010, 33(2): 279–287. doi: 10.3724/SP.J.1016.2010.00279 ZHOU Zhihua, ZHANG Minling, HUANG Shengjun, et al. Multi-instance multi-label learning[J]. Artificial Intelligence, 2012, 176(1): 2291–2320. doi: 10.1016/j.artint.2011.10.002 PAPINENI K, ROUKOS S, WARD T, et al. BLEU: A method for automatic evaluation of machine translation[C]. The 40th Annual Meeting on Association for Computational Linguistics, Philadelphia, USA, 2002: 311–318. doi: 10.3115/1073083.1073135. -





 下载:
下载:


 下载:
下载:
