A New Link Prediction Method for Complex Networks Based onTopological Effectiveness of Resource Transmission Paths
-
摘要:
链路预测旨在利用网络中已有的拓扑结构或其他信息,预测未连边节点间存在连接的可能性。资源分配指标具有较低复杂度的同时取得了较好的预测效果,但在资源传输过程的描述中缺少对路径有效性的刻画。资源传输过程是网络演化连边产生的重要内在动力,通过分析节点间资源传输路径周围拓扑的有效性,该文提出一种基于资源传输路径有效性的链路预测方法。该方法首先分析了节点间潜在的资源传输路径对资源传输量的影响,提出资源传输路径有效性的量化方法。然后,基于资源传输路径的有效性,通过对双向资源传输量进行刻画,提出了节点间传输路径的有效性指标。在12个实际网络数据集上的实验测试表明,相比其他基于相似性的链路预测方法,该方法在AUC和Precision衡量标准下能够取得更好的效果。
Abstract:Link prediction considers to discover the unknown or missing links of complex networks by using the existing topology or other information. Resource Allocation index can achieve a good performance with low complexity. However, it ignores the path effectiveness of resource transmission process. The resource transmission process is an important internal driving force for the evolution of the network. By analyzing the effectiveness of the topology around the resource transmission path between nodes, a link prediction method based on topological effectiveness of resource transmission paths is proposed. Firstly, the influence of potential resource transmission paths between nodes on resource transmission is analyzed, and a quantitative method for resource transmission path effectiveness is proposed. Then, based on the effectiveness of the resource transmission path, after studying the two-way resource transmission amount between two nodes, the transmission path effectiveness index is proposed. The experimental results of 12 real networks show that compared with other link prediction methods, the proposed method can achieve higher prediction accuracy under the AUC and Precision metrics.
-
Key words:
- Complex network /
- Link prediction /
- Resource transmission path /
- Effectiveness
-
表 1 网络数据特征参数
网络 AIDS FWEW HS Figeys UC Metbolic 节点数 146 69 1858 2239 1899 453 边数 180 880 12534 6432 13838 2025 集聚系数 2.47 25.51 13.49 5.76 14.57 8.94 平均度 3.42 1.64 3.39 3.98 3.06 2.66 平均路径 –0.725 –0.298 –0.085 –0.331 –0.188 –0.226 匹配系数 0.052 0.552 0.0904 0.04 0.109 0.647 表 2 AUC结果对比分析
方法 AIDS FWEW HS Figeys UC Metbolic CN 0.599 0.684 0.812 0.566 0.781 0.921 RA 0.609 0.702 0.816 0.570 0.787 0.959 AA 0.609 0.695 0.815 0.569 0.787 0.955 CAR 0.599 0.685 0.812 0.567 0.783 0.920 LP(a) 0.836 0.702 0.933 0.888 0.893 0.920 LP(b) 0.833 0.728 0.940 0.903 0.903 0.921 Katz(a) 0.854 0.704 0.933 0.887 0.893 0.920 Katz(b) 0.852 0.734 0.937 0.898 0.903 0.920 ACT 0.954 0.779 0.868 0.917 0.896 0.767 Cos+ 0.591 0.510 0.960 0.844 0.869 0.904 本文方法 0.961 0.827 0.971 0.952 0.929 0.964 (a)可调参数$\alpha {\rm{ = 0}}{\rm{.001}}$ (b)可调参数$\alpha {\rm{ = 0}}{\rm{.01}}$ 表 3 Pre结果对比
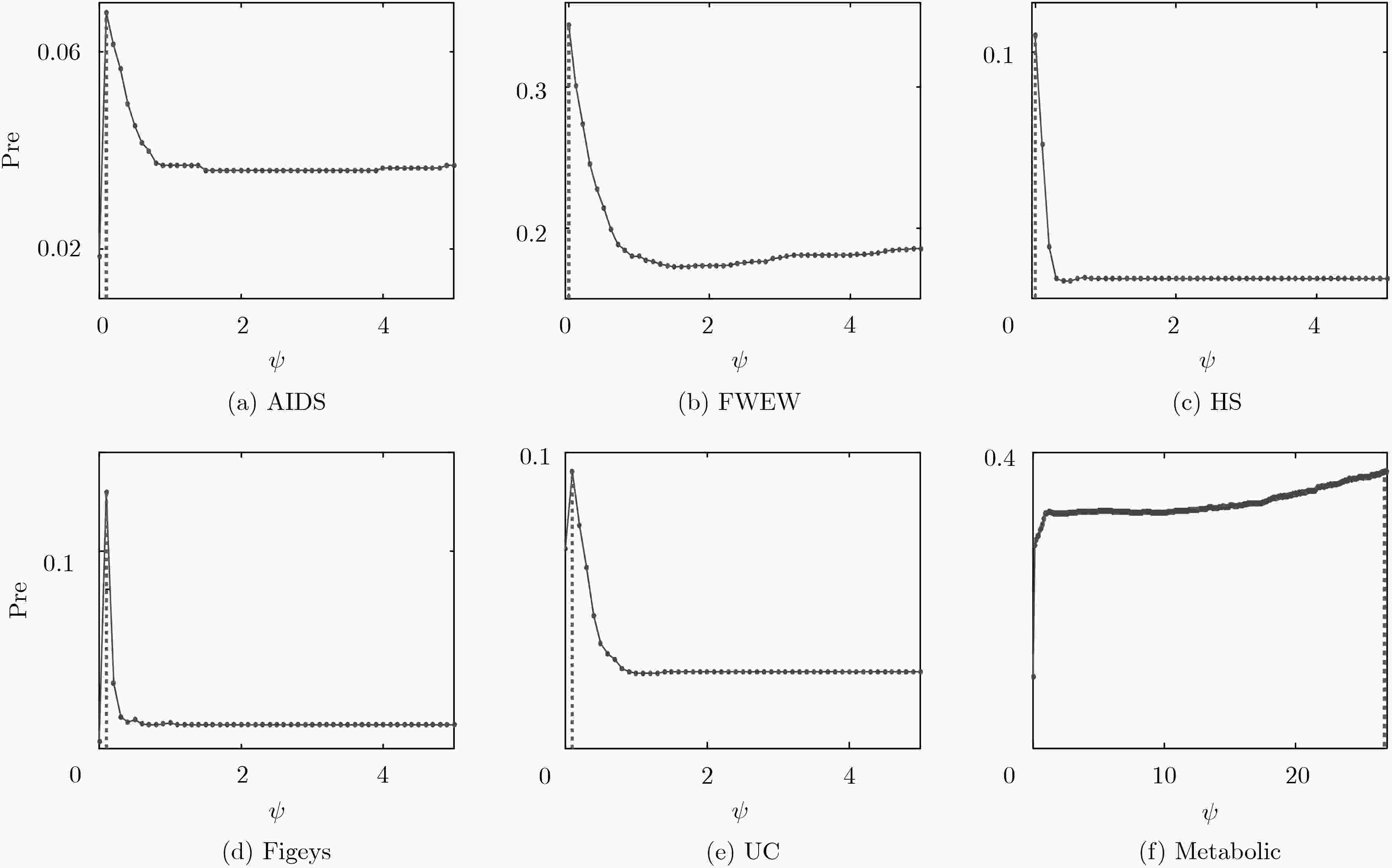
方法 AIDS FWEW HS Figeys UC Metbolic CN 0.019 0.143 0.017 0.011 0.034 0.202 RA 0.028 0.165 0.008 0.012 0.026 0.319 AA 0.028 0.152 0.012 0.012 0.033 0.252 CAR 0.019 0.137 0.033 0.025 0.064 0.193 LP(a) 0.055 0.153 0.021 0.011 0.034 0.202 LP(b) 0.055 0.180 0.055 0.012 0.053 0.200 Katz(a) 0.055 0.153 0.021 0.010 0.034 0.202 Katz(b) 0.055 0.183 0.071 0.011 0.054 0.198 ACT 0.000 0.128 0.000 0.000 0.000 0.000 Cos+ 0.000 0.000 0.015 0.005 0.010 0.097 本文方法 0.068 0.344 0.107 0.130 0.093 0.374 (a)可调参数$\alpha {\rm{ = 0}}{\rm{.001}}$ (b)可调参数$\alpha {\rm{ = 0}}{\rm{.01}}$ -
WANG Minggang, ZHAO Longfeng, DU Ruijin, et al. A novel hybrid method of forecasting crude oil prices using complex network science and artificial intelligence algorithms[J]. Applied Energy, 2018, 220: 480–495. doi: 10.1016/j.apenergy.2018.03.148 GOSAK M, MARKOVIČ R, DOLENŠEK J, et al. Network science of biological systems at different scales: A review[J]. Physics of Life Reviews, 2018, 24: 118–135. doi: 10.1016/j.plrev.2017.11.003 DU Wenbo, ZHANG Mingyuan, YING Wen, et al. The networked evolutionary algorithm: A network science perspective[J]. Applied Mathematics and Computation, 2018, 338: 33–43. doi: 10.1016/j.amc.2018.06.002 CHEN Zhenhao, WU Jiajing, XIA Yongxiang, et al. Robustness of interdependent power grids and communication networks: A complex network perspective[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2018, 65(1): 115–119. doi: 10.1109/TCSII.2017.2705758 王凯, 刘树新, 陈鸿昶, 等. 一种基于节点间资源承载度的链路预测方法[J]. 电子与信息学报, 2019, 41(5): 1225–1234. doi: 10.11999/JEIT180553WANG Kai, LIU Shuxin, CHEN Hongchang, et al. A new link prediction method for complex networks based on resources carrying capacity between nodes[J]. Journal of Electronics &Information Technology, 2019, 41(5): 1225–1234. doi: 10.11999/JEIT180553 BENSON A R, ABEBE R, SCHAUB M T, et al. Simplicial closure and higher-order link prediction[J]. The National Academy of Sciences of the United States of America, 2018, 115(48): E11221–E11230. doi: 10.1073/pnas.1800683115 LIU Shuxin, JI Xinsheng, LIU Caixia, et al. Similarity indices based on link weight assignment for link prediction of unweighted complex networks[J]. International Journal of Modern Physics B, 2017, 31(2): 1650254. doi: 10.1142/S0217979216502544 LORRAIN F and WHITE H C. Structural Equivalence of Individuals in Social Networks[M]. LEINHARDT S. Social Networks: A Developing Paradigm. Lausanne: Academic Press, 1977: 67-98. doi: 10.1080/0022250X.1971.9989788. ZHOU Tao, LÜ Linyuan, and ZHANG Yicheng. Predicting missing links via local information[J]. The European Physical Journal B, 2009, 71(4): 623–630. doi: 10.1140/epjb/e2009-00335-8 ADAMIC L A and ADAR E. Friends and neighbors on the web[J]. Social Networks, 2003, 25(3): 211–230. doi: 10.1016/S0378-8733(03)00009-1 CANNISTRACI C V, ALANIS-LOBATO G, and RAVASI T. From link-prediction in brain connectomes and protein interactomes to the local-community-paradigm in complex networks[J]. Scientific Reports, 2013, 3: 1613. doi: 10.1038/srep01613 XIE Yanbo, ZHOU Tao, and WANG Binhong. Scale-free networks without growth[J]. Physica A: Statistical Mechanics and its Applications, 2008, 387(7): 1683–1688. doi: 10.1016/j.physa.2007.11.005 SALTON G and MCGILL M J. Introduction to Modern Information Retrieval[M]. New York: McGraw-Hill, 1986. LÜ Linyuan, JIN Cihang, and ZHOU Tao. Similarity index based on local paths for link prediction of complex networks[J]. Physical Review E, 2009, 80(4): 046122. doi: 10.1103/PhysRevE.80.046122 LIU Shuxin, JI Xinsheng, LIU Caixia, et al. Extended resource allocation index for link prediction of complex network[J]. Physica A: Statistical Mechanics and Its Applications, 2017, 479: 174–183. doi: 10.1016/j.physa.2017.02.078 KATZ L. A new status index derived from sociometric analysis[J]. Psychometrika, 1953, 18(1): 39–43. doi: 10.1007/BF02289026 KLEIN D J and RANDIĆ M. Resistance distance[J]. Journal of Mathematical Chemistry, 1993, 12(1): 81–95. doi: 10.1007/BF01164627 FOUSS F, PIROTTE A, RENDERS J M, et al. Random-walk computation of similarities between nodes of a graph with application to collaborative recommendation[J]. IEEE Transactions on Knowledge and Data Engineering, 2007, 19(3): 355–369. doi: 10.1109/tkde.2007.46 BRIN S and PAGE L. The anatomy of a large-scale hypertextual Web search engine[J]. Computer Networks and ISDN Systems, 1998, 30(1/7): 107–117. doi: 10.1016/s0169-7552(98)00110-x YANG Dingda, LIAO Xiangwen, SHEN Huawei, et al. Dynamic node immunization for restraint of harmful information diffusion in social networks[J]. Physica A: Statistical Mechanics and Its Applications, 2018, 503: 640–649. doi: 10.1016/j.physa.2018.02.128 刘树新, 季新生, 刘彩霞, 等. 一种信息传播促进网络增长的网络演化模型[J]. 物理学报, 2014, 63(15): 158902. doi: 10.7498/aps.63.158902LIU Shuxin, JI Xinsheng, LIU Caixia, et al. A complex network evolution model for network growth promoted by information transmission[J]. Acta Physica Sinica, 2014, 63(15): 158902. doi: 10.7498/aps.63.158902 YAO Yabing, ZHANG Ruisheng, YANG Fan, et al. Link prediction in complex networks based on the interactions among paths[J]. Physica A: Statistical Mechanics and Its Applications, 2018, 510: 52–67. doi: 10.1016/j.physa.2018.06.051 LIU Liang, QU Bo, CHEN Bin, et al. Modelling of information diffusion on social networks with applications to WeChat[J]. Physica A: Statistical Mechanics and Its Applications, 2018, 496: 318–329. doi: 10.1016/j.physa.2017.12.026 SATHIYAKUMARI K and VIJAYA M S. Identification of Subgroups in a Directed Social Network Using Edge Betweenness and Random Walks[M]. SATAPATHY S C, BHATEJA V, and DAS S. Smart Computing and Informatics. Singapore: Springer, 2018: 115-125. doi: 10.1007/978-981-10-5544-7_12. WU Yiteng, YU Hongtao, ZHANG Jianpeng, et al. USI-AUC: An evaluation criterion of community detection based on a novel link-prediction method[J]. Intelligent Data Analysis, 2018, 22(2): 439–462. doi: 10.3233/IDA-173400 CHUAN P M, SON L H, ALI M, et al. Link prediction in co-authorship networks based on hybrid content similarity metric[J]. Applied Intelligence, 2018, 48(8): 2470–2486. doi: 10.1007/s10489-017-1086-x -





 下载:
下载:



 下载:
下载:
