Specific Emitter Identification Using Signal Trajectory Image
-
摘要:
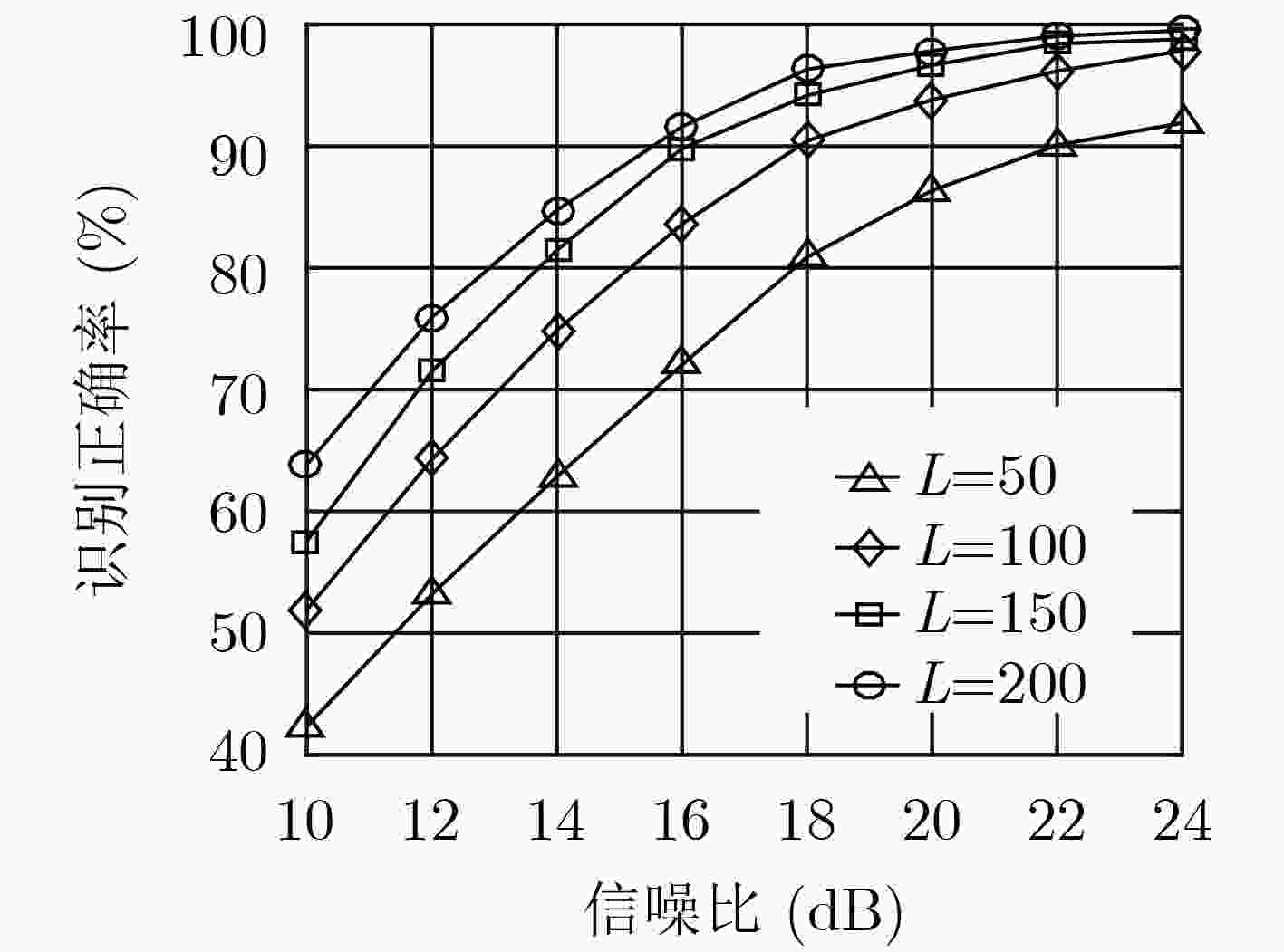
发射机的指纹特征具有复杂性,现有的认识水平制约了特定辐射源识别(SEI)的性能。为此,该文提出一种基于矢量图的SEI方法,应用深度学习技术实现了多种复杂特征的联合提取。该文首先分析了多种发射机畸变在矢量图上的视觉表现;在此基础上,以矢量图灰度图像作为信号表示,构建深度残差网络提取图像中的视觉特征。该方法克服了现有认知的局限,兼具高信息完整性和低计算复杂度。实验结果表明,与现有算法相比,该方法能够显著改善SEI的性能,识别增益约为30%。
Abstract:The radio frequency fingerprinting of the emitter is complex, and the performance of Specific Emitter Identification (SEI) is subjected to the present expertise. To remedy this shortcoming, this paper presents a novel SEI algorithm based on signal trajectory image, which realizes joint extraction of multiple complex fingerprints using deep learning architecture. First, this paper analyses the visual characteristics of multiple emitter imperfections in the signal trajectory image. Thereafter, signal trajectory grayscale image is used as the signal representation. Finally, a deep residual network is constructed to learn the visual characteristics reflected in the images. The proposed method overcomes the limitations of existing knowledge, and combines high information integrity with low computational complexity. Simulation results demonstrate that, compared with the existing algorithms, the proposed one can remarkably improve the SEI performance with a gain of about 30%.
-
表 1 不同算法的复杂度对比
算法 文献[6]算法 文献[8]算法 文献[9]算法 文献[10]算法 文献[14]算法 本文算法 复杂度 $O\left( {ML\lg \left( {ML} \right)} \right) + O\left( S \right)$ $O\left( {ML} \right) + O\left( L \right)$ $O\left( {ML} \right) + O\left( L \right)$ $O\left( {ML} \right) + O\left( L \right)$ $O\left( {PQ\lg Q} \right) + O\left( S \right)$ $O\left( {ML} \right) + O\left( S \right)$ 表 2 不同辐射源的畸变参数
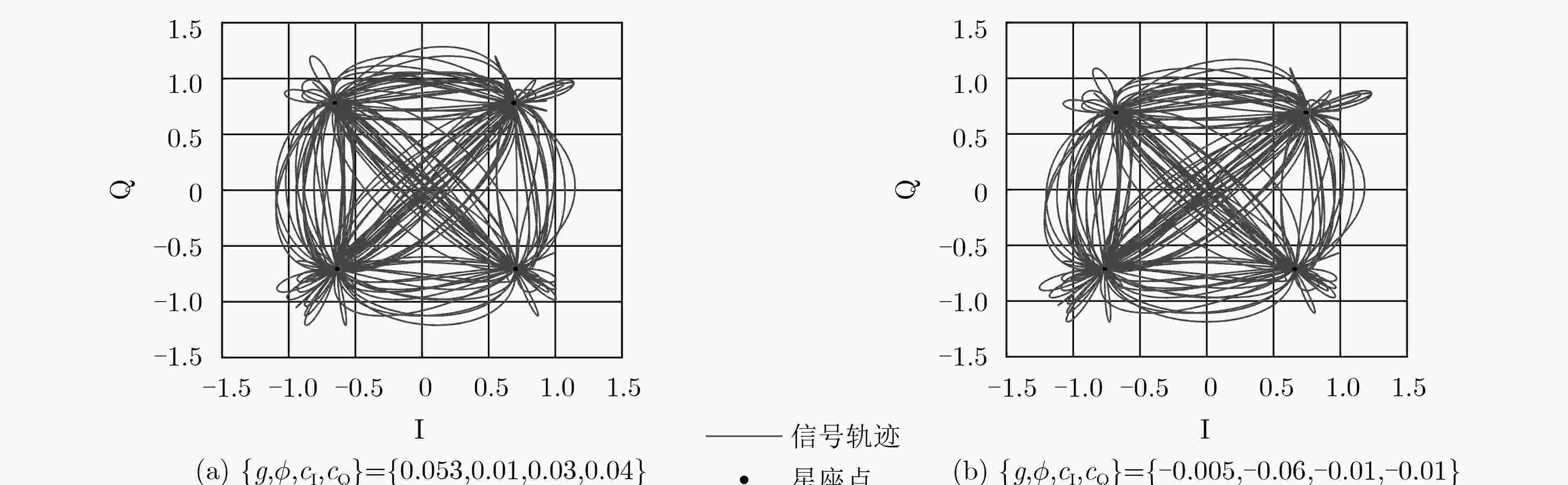
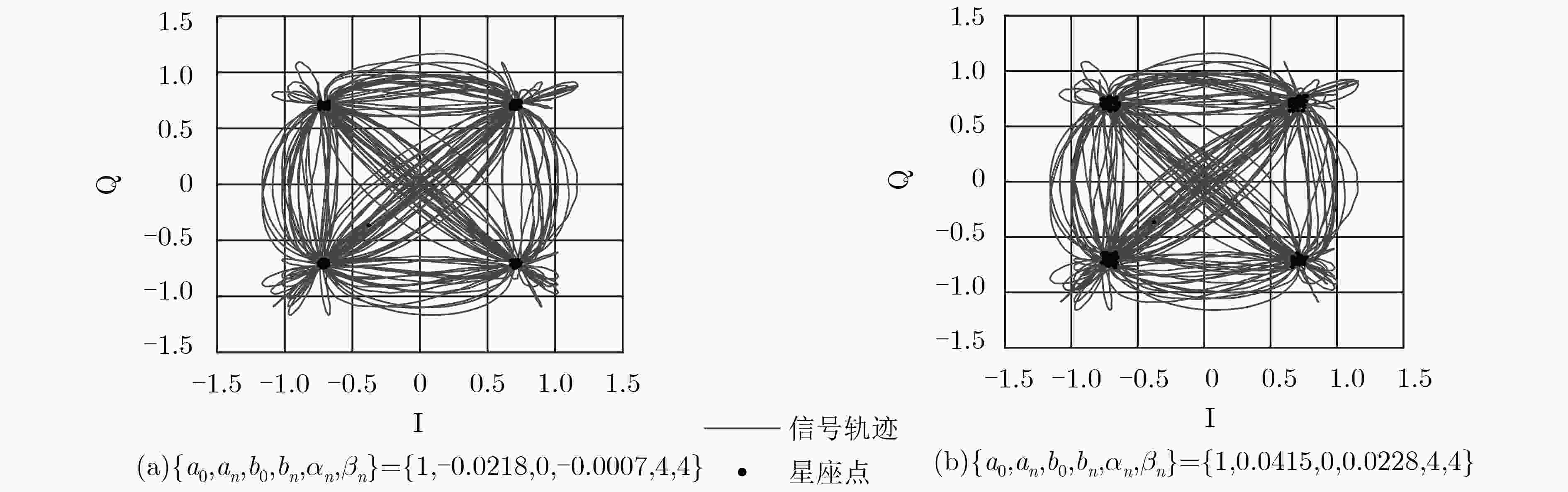
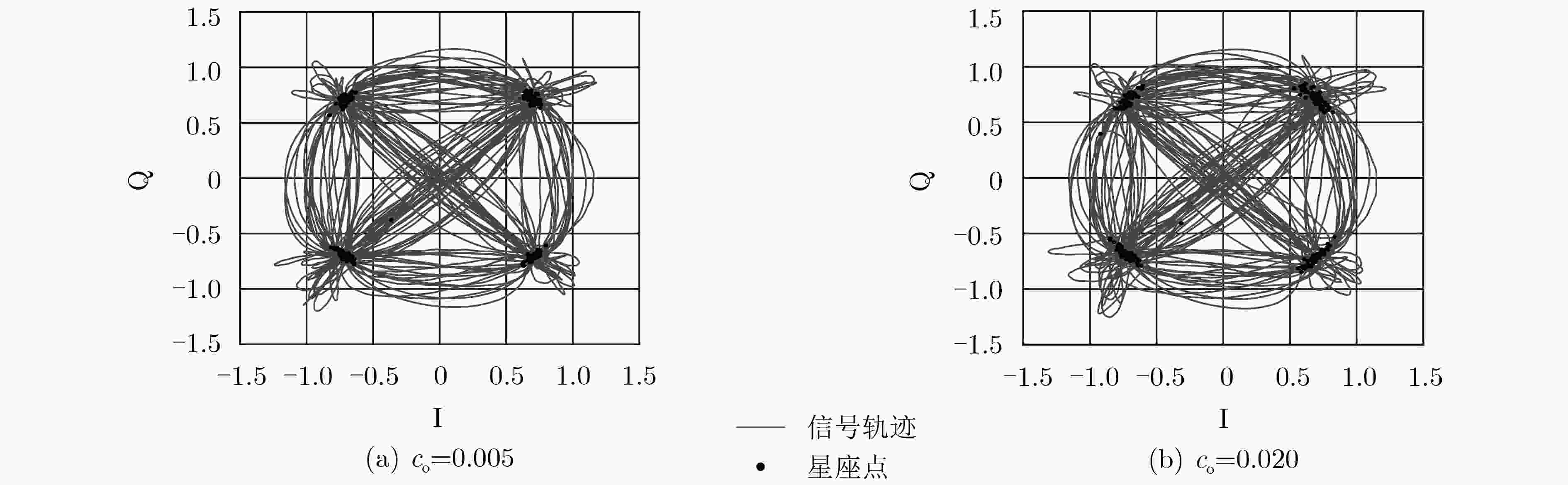
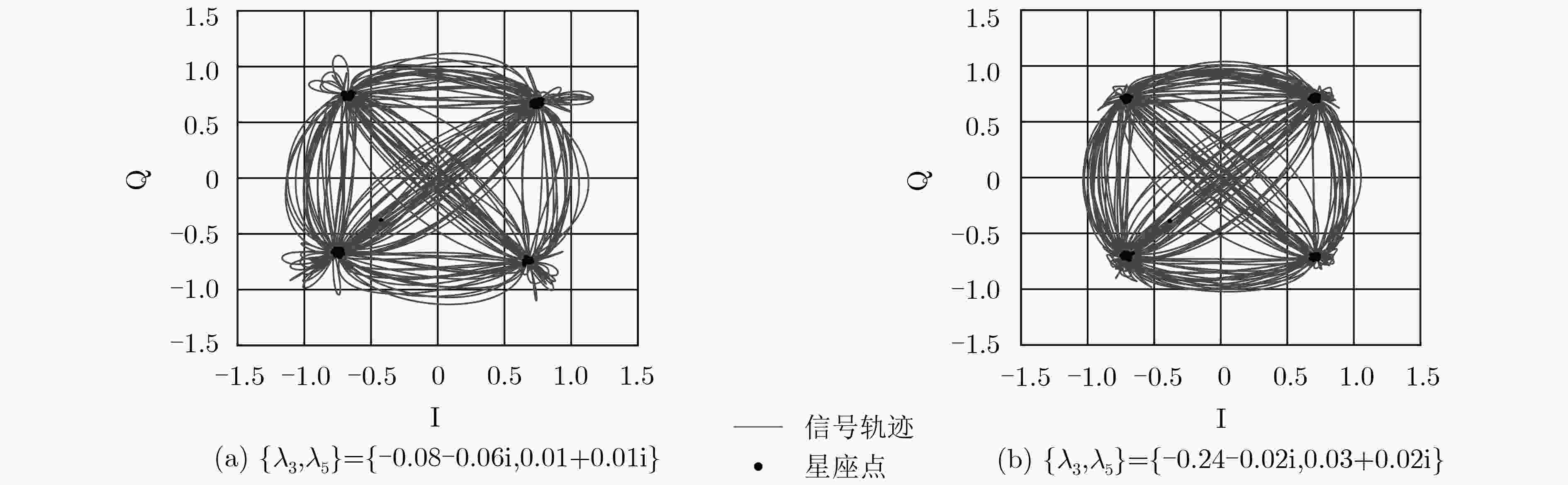
辐射源 1 2 3 4 5 6 7 $g$ 0.0299 0.0188 0.0081 –0.0025 –0.0128 –0.0230 –0.0329 $\phi $ 0.0137 0.0093 0.0050 0.0006 –0.0038 –0.0081 –0.0125 ${c_{\rm I}}$ 0.0142 0.0097 0.0052 0.0007 –0.0038 –0.0083 –0.0128 ${c_{\rm Q}}$ 0.0147 0.0102 0.0057 0.0012 –0.0033 –0.0078 –0.0123 ${a_n}$ –0.0640 –0.0429 –0.0218 –0.0007 0.0204 0.0415 0.0627 ${b_n}$ –0.0740 –0.0498 –0.0256 –0.0014 0.0228 0.0470 0.0713 ${c_{\rm o}}$ 0.0002 0.0010 0.0018 0.0026 0.0034 0.0042 0.0050 ${\lambda _3}$ –0.2915–0.0079i –0.0003–0.0004i –0.4371–0.0092i –0.1459–0.0066i –0.5827–0.0096i –0.0731–0.0042i –0.3643–0.0085i ${\lambda _5}$ 0.0295+0.0005i 0.0001+0.0004i 0.0821+0.0048i 0.0338+0.0014i 0.0537+0.0029i 0.0571+0.0035i 0.0484+0.0022i 表 3 网络结构及其参数量和单批次训练时间
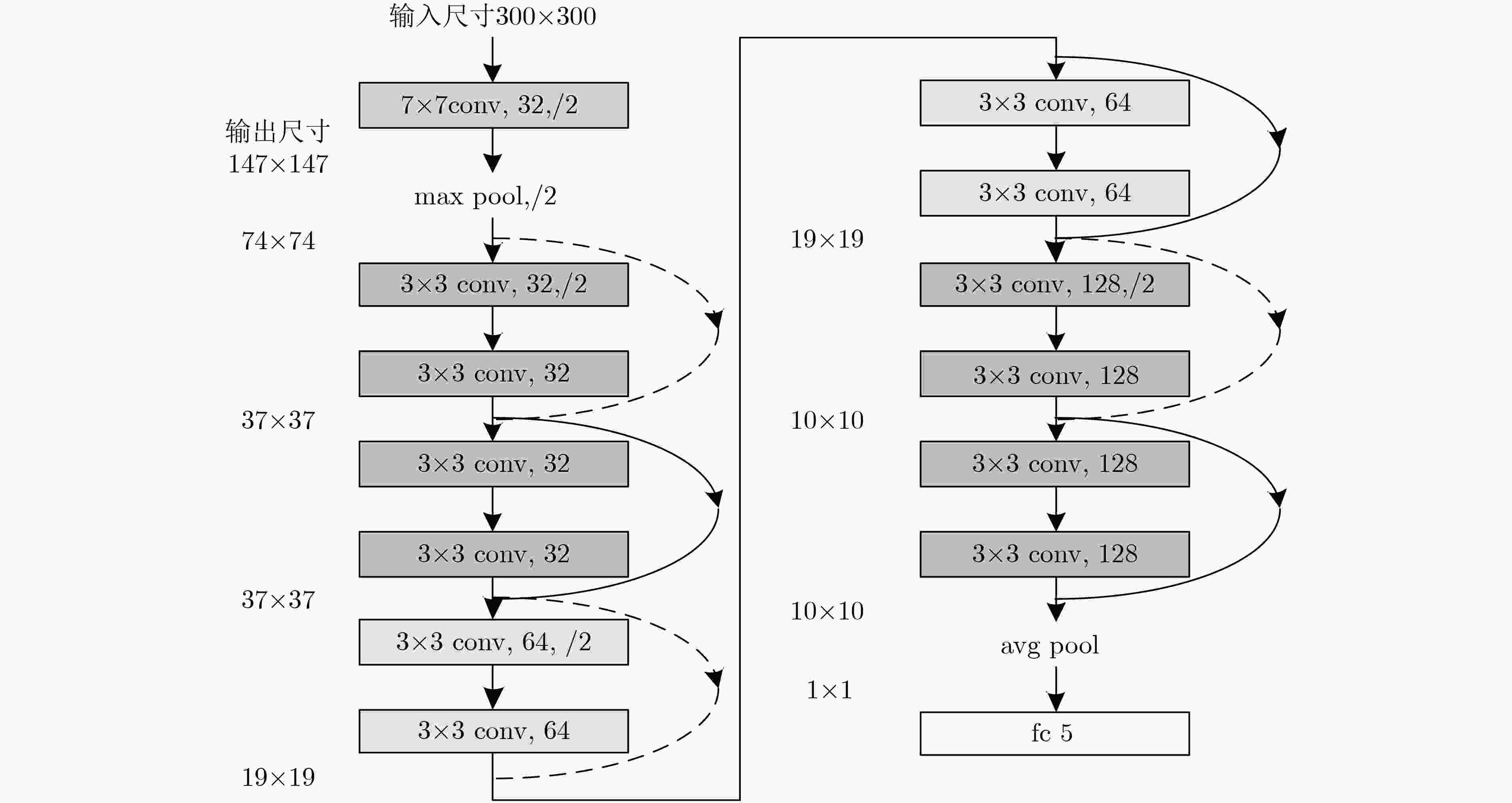
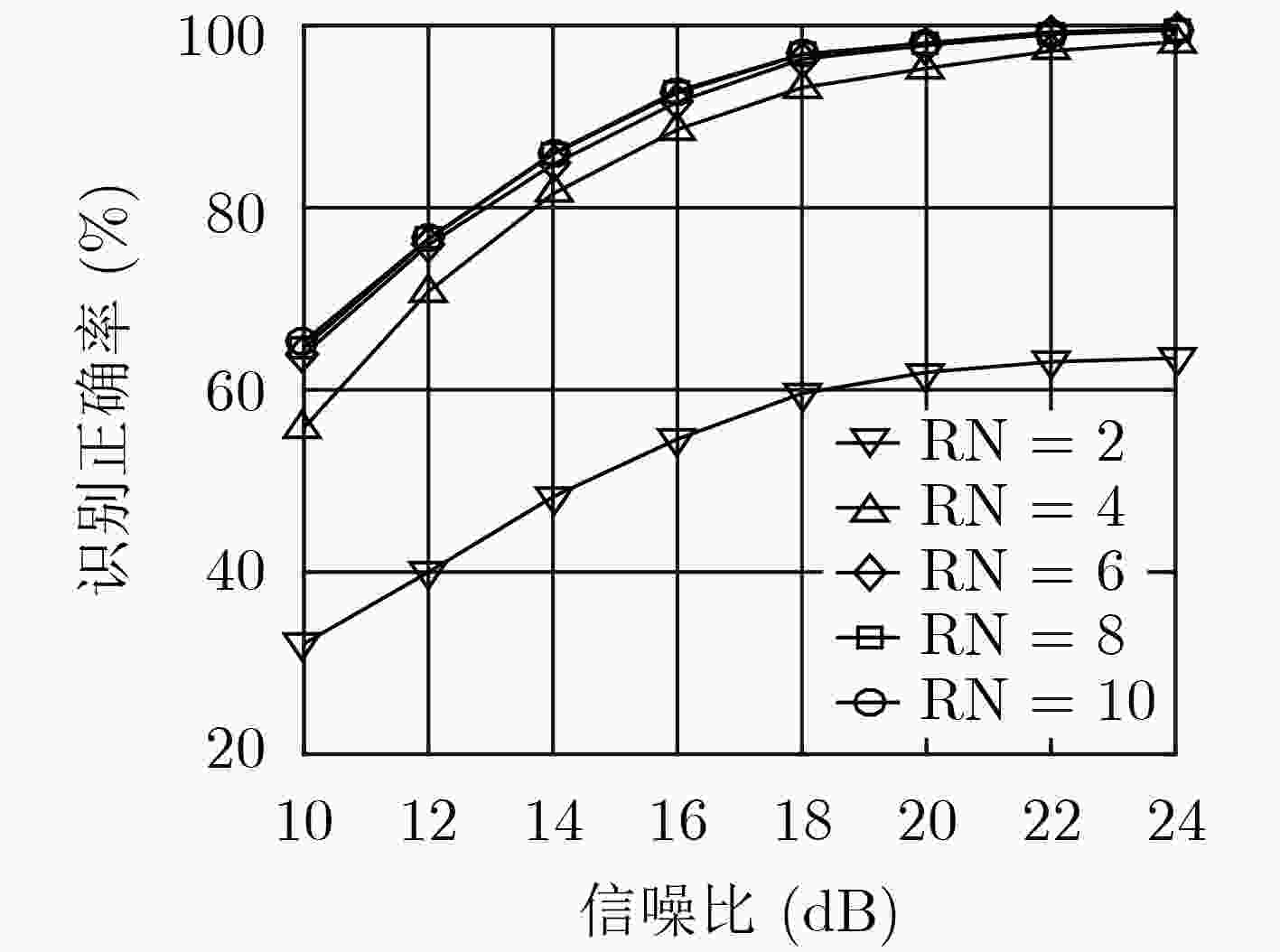
RN 2 4 6 8 10 conv1 7×7, 32, stride2 max pool 3×3, stride 2 conv2_x $\left[ \begin{array}{l} 3 \times 3,32 \\ 3 \times 3,32 \\ \end{array} \right] \times 2$ $\left[ \begin{array}{l} 3 \times 3,32 \\ 3 \times 3,32 \\ \end{array} \right] \times 2$ $\left[ \begin{array}{l} 3 \times 3,32 \\ 3 \times 3,32 \\ \end{array} \right] \times 2$ $\left[ \begin{array}{l} 3 \times 3,32 \\ 3 \times 3,32 \\ \end{array} \right] \times 2$ $\left[ \begin{array}{l} 3 \times 3,32 \\ 3 \times 3,32 \\ \end{array} \right] \times 2$ conv3_x — $\left[ \begin{array}{l} 3 \times 3,64 \\ 3 \times 3,64 \\ \end{array} \right] \times 2$ $\left[ \begin{array}{l} 3 \times 3,64 \\ 3 \times 3,64 \\ \end{array} \right] \times 2$ $\left[ \begin{array}{l} 3 \times 3,64 \\ 3 \times 3,64 \\ \end{array} \right] \times 2$ $\left[ \begin{array}{l} 3 \times 3,64 \\ 3 \times 3,64 \\ \end{array} \right] \times 2$ conv4_x — — $\left[ \begin{array}{l} 3 \times 3,128 \\ 3 \times 3,128 \\ \end{array} \right] \times 2$ $\left[ \begin{array}{l} 3 \times 3,128 \\ 3 \times 3,128 \\ \end{array} \right] \times 2$ $\left[ \begin{array}{l} 3 \times 3,128 \\ 3 \times 3,128 \\ \end{array} \right] \times 2$ conv5_x — — — $\left[ \begin{array}{l} 3 \times 3,256 \\ 3 \times 3,256 \\ \end{array} \right] \times 2$ $\left[ \begin{array}{l} 3 \times 3,256 \\ 3 \times 3,256 \\ \end{array} \right] \times 2$ conv6_x — — — — $\left[ \begin{array}{l} 3 \times 3,512 \\ 3 \times 3,512 \\ \end{array} \right] \times 2$ avg pool 5-d fc, softmax 参数量 3.9×104 1.7×105 6.8×105 2.7×106 1.1×107 训练时间 (s) 0.3516 0.3858 0.4019 0.4262 0.4584 -
DANEV B, ZANETTI D, and CAPKUN S. On physical-layer identification of wireless devices[J]. ACM Computing Surveys, 2012, 45(1): 1–29. doi: 10.1145/2379776.2379782 SPEZIO A E. Electronic warfare systems[J]. IEEE Transactions on Microwave Theory and Techniques, 2002, 50(3): 633–644. doi: 10.1109/22.989948 MERCHANT K, REVAY S, STANTCHEV G, et al. Deep learning for RF device fingerprinting in cognitive communication networks[J]. IEEE Journal of Selected Topics in Signal Processing, 2018, 12(1): 160–167. doi: 10.1109/JSTSP.2018.2796446 HAN Jie, ZHANG Tao, REN Dongfang, et al. Communication emitter identification based on distribution of bispectrum amplitude and phase[J]. IET Science, Measurement & Technology, 2017, 11(8): 1104–1112. doi: 10.1049/iet-smt.2017.0024 BERTONCINI C, RUDD K, NOUSAIN B, et al. Wavelet fingerprinting of radio-frequency identification (RFID) tags[J]. IEEE Transactions on Industrial Electronics, 2012, 59(12): 4843–4850. doi: 10.1109/TIE.2011.2179276 ZHANG Jingwen, WANG Fanggang, DOBRE O A, et al. Specific emitter identification via Hilbert-Huang transform in single-hop and relaying scenarios[J]. IEEE Transactions on Information Forensics and Security, 2016, 11(6): 1192–1205. doi: 10.1109/TIFS.2016.2520908 SATIJA U, TRIVEDI N, BISWAL G, et al. Specific emitter identification based on variational mode decomposition and spectral features in single hop and relaying scenarios[J]. IEEE Transactions on Information Forensics and Security, 2019, 14(3): 581–591. doi: 10.1109/TIFS.2018.2855665 BRIK V, BANERJEE S, GRUTESER M, et al. Wireless device identification with radiometric signatures[C]. The 14th ACM International Conference on Mobile Computing and Networking, San Francisco, USA, 2008: 116–127. HUANG Yuanling and ZHENG Hui. Radio frequency fingerprinting based on the constellation errors[C]. The 18th Asia-Pacific Conference on Communications, Jeju Island, South Korea, 2012: 900–905. 彭林宁, 胡爱群, 朱长明, 等. 基于星座轨迹图的射频指纹提取方法[J]. 信息安全学报, 2016, 1(1): 50–58. doi: 10.19363/j.cnki.cn10-1380/tn.2016.01.007PENG Linning, HU Aiqun, ZHU Changming, et al. Radio fingerprint extraction based on constellation trace figure[J]. Journal of Cyber Security, 2016, 1(1): 50–58. doi: 10.19363/j.cnki.cn10-1380/tn.2016.01.007 O’SHEA T J, ROY T, and CLANCY T C. Over-the-air deep learning based radio signal classification[J]. IEEE Journal of Selected Topics in Signal Processing, 2018, 12(1): 168–179. doi: 10.1109/JSTSP.2018.2797022 KULIN M, KAZAZ T, MOERMAN I, et al. End-to-end learning from spectrum data: A deep learning approach for wireless signal identification in spectrum monitoring applications[J]. IEEE Access, 2018, 6: 18484–18501. doi: 10.1109/ACCESS.2018.2818794 RIYAZ S, SANKHE K, IOANNIDIS S, et al. Deep learning convolutional neural networks for radio identification[J]. IEEE Communications Magazine, 2018, 56(9): 146–152. doi: 10.1109/MCOM.2018.1800153 DING Lida, WANG Shilian, WANG Fanggang, et al. Specific emitter identification via convolutional neural networks[J]. IEEE Communications Letters, 2018, 22(12): 2591–2594. doi: 10.1109/LCOMM.2018.2871465 Agilent Technologies. Agilent technologies wireless test solutions application note 1313: Testing and troubleshooting digital RF communications transmitter designs[EB/OL]. http://literature.cdn.keysight.com/litweb/pdf/5968-3578E.pdf, 2016. SRIDHARAN G. Phase noise in multi-carrier systems[D]. [Master dissertation], University of Toronto, 2010: 9–44. HE Kaiming, ZHANG Xiangyu, REN Shaoqing, et al. Deep residual learning for image recognition[C]. 2016 IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, USA, 2016: 770–778. -





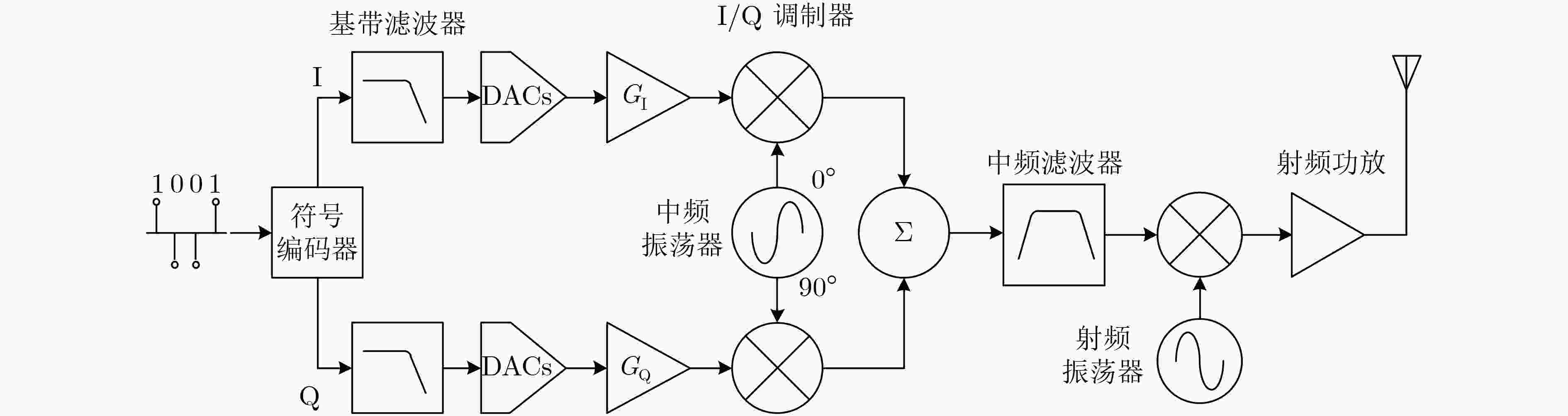
 下载:
下载:

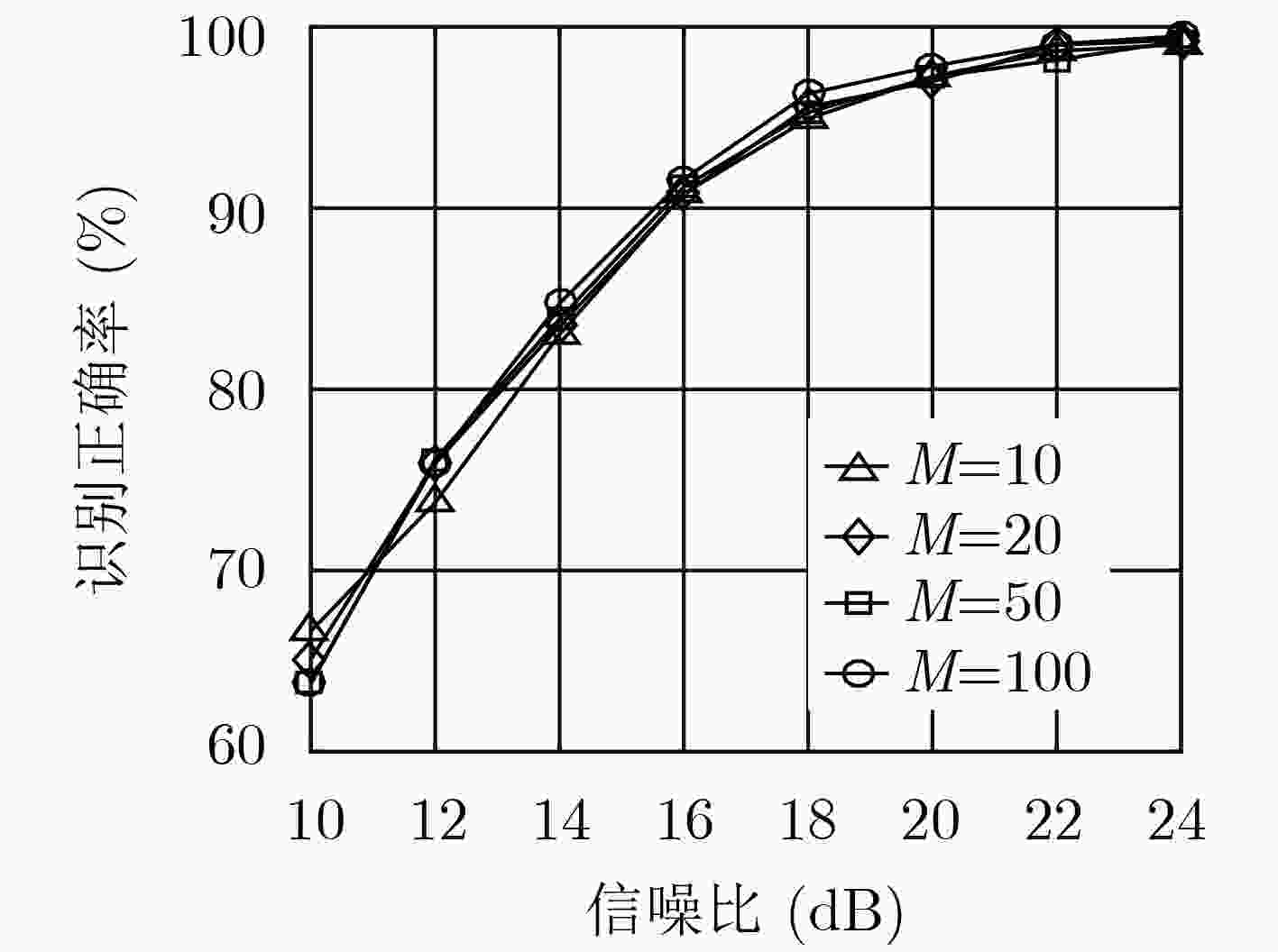
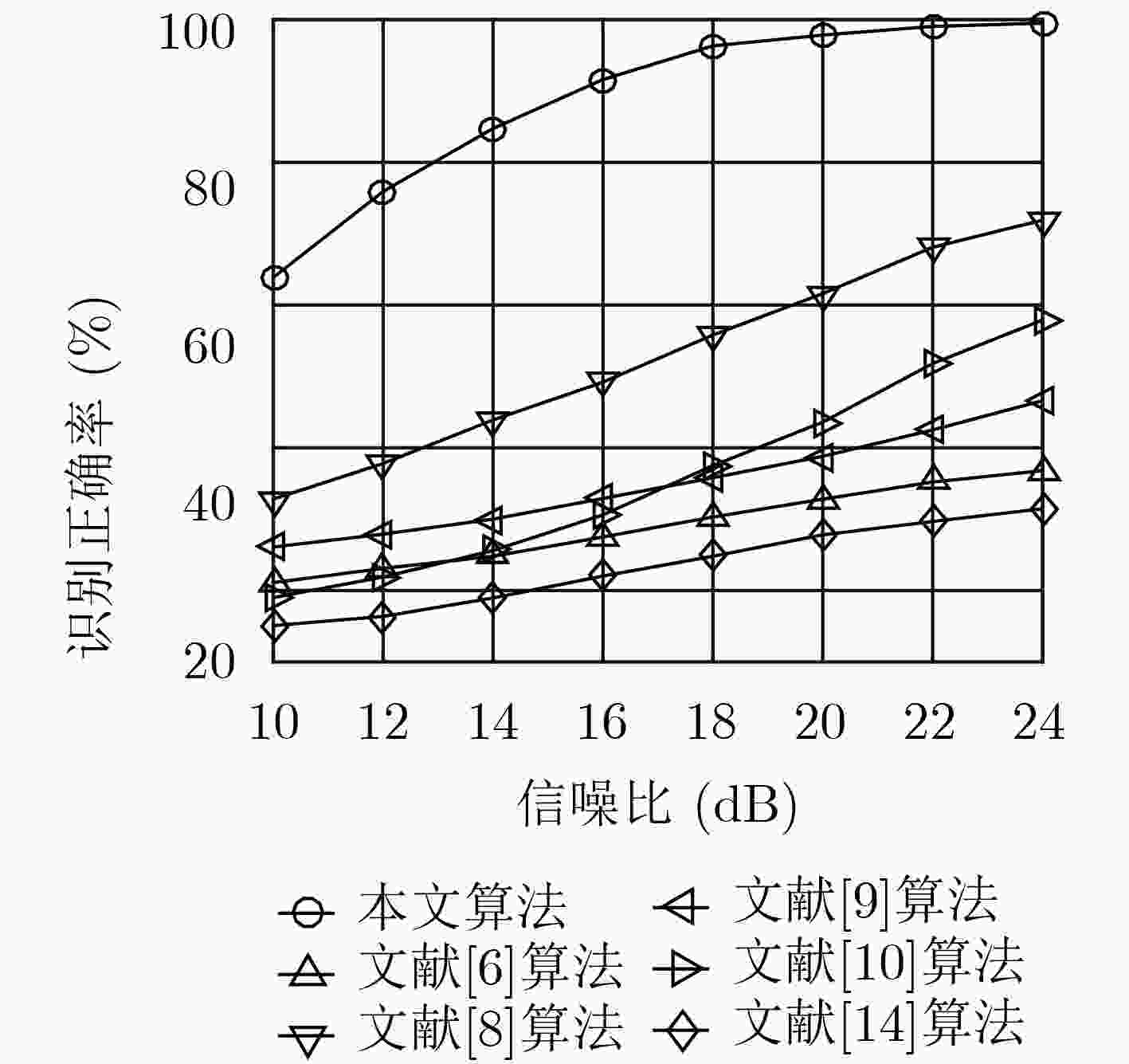


 下载:
下载:
