Joint Resource Allocation Algorithms Based on Mixed Cloud/Fog Computing in Vehicular Network
-
摘要:
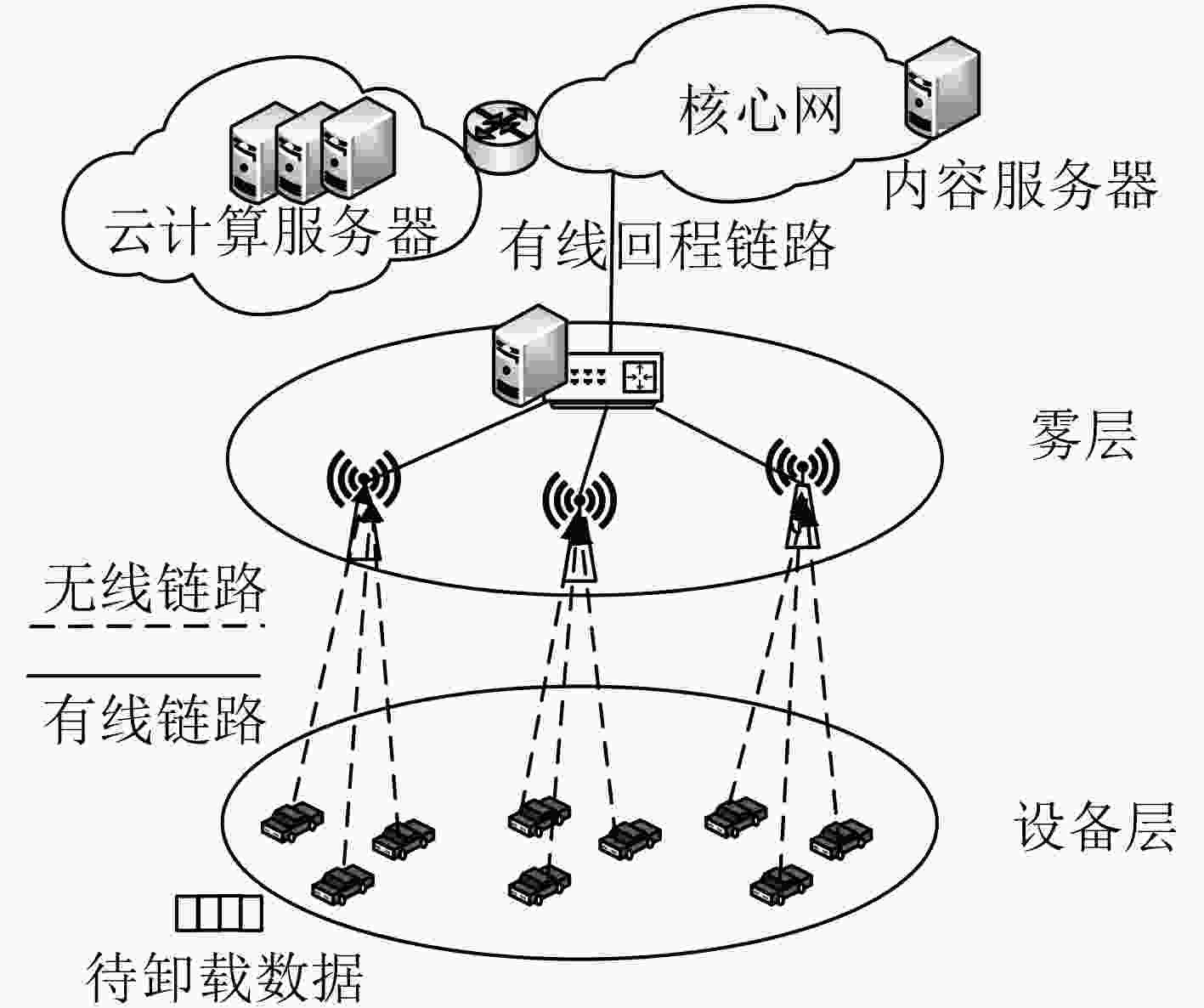
针对车联网业务的低时延、低功耗需求及海量设备计算卸载引起的网络拥塞问题,该文提出一种在云雾混合网络架构下的联合计算卸载、计算资源和无线资源分配算法(JODRAA)。首先,该算法考虑将云计算与雾计算结合,以最大时延作为约束,建立最小化系统能耗和资源成本的资源优化模型。其次,将原问题转化为标准二次约束二次规划(QCQP)问题,并设计一种低复杂度的联合卸载决策和计算资源分配算法。进一步,针对海量设备计算卸载引起的网络拥塞问题,建立卸载用户接入请求队列的上溢概率估计模型,提出一种基于在线测量的雾节点时频资源配置算法。最后,借助分式规划理论和拉格朗日对偶分解方法得到迭代的带宽和功率分配策略。仿真结果表明,该文算法可以在满足时延需求的前提下,最小化系统能耗和资源成本。
Abstract:For the problems of low delay, low power requirement and access congestion caused by computational unloading of mass devices, a Joint Offloading Decision and Resource Allocation Algorithm (JODRAA) is proposed based on cloud-fog hybrid network architecture. Firstly, the algorithm considers the combination of cloud and fog computing, and establishes a resource optimization model to minimize system energy consumption and resource cost with maximum delay as constraint. Secondly, the original problem is transformed into a standard Quadratically Constrained Quadratic Program (QCQP) problem, and a low-complexity joint unloading decision-making and computational resource allocation algorithm is designed. Furthermore, considering the access congestion problem caused by massive computing of unloading devices, an estimation model of the overflow probability of unloading user access request queue is established, and an on-line measurement based time-frequency resource allocation algorithm for fog nodes is proposed. Finally, the iterative bandwidth and power allocation strategy is obtained by using fractional programming theory and Lagrange dual decomposition method. The simulation results show that the proposed algorithm can minimize the system energy consumption and resource cost on the premise of time delay.
-
Key words:
- Vehicular network /
- Fog computing /
- Computation offload /
- Resource allocation
-
表 1 联合卸载决策和基于二分法的计算资源调度算法
1. 初始化试验次数$J$,用户数$M$,总带宽$B_f^{\max }$及资源块带宽${B_{SC}}$
及总计算资源${F^{{\rm{fog}}}}$,初始化用户参数${D_m}$, ${u_m}$, $f_m^{{\rm{loc}}}$, $p_m^{\max }$,
$p_m^{{\rm{id}}}$, $p_m^{{\rm{loc}}}$, $R_m^{{\rm{fc}}}$, $f_m^c$, $d_m^{\max }$,初始化式(17)中的所有矩阵2. 利用凸优化工具求解式(17)得到优化解${{{Q}}^*}$ 3. 从优化解${{{Q}}^{\rm{*}}}$中提取左上角$2M \times 2M$的子矩阵${{{Q}}^{'*}}$, ${{{Q}}^{'*}}$中的
对角线上的元素值为$\Pr = \left[ { {\rm{pr} }_1^f,{\rm{pr} }_1^{\rm c},...,{\rm{pr} }_M^f,{\rm{pr} }_M^{\rm c}} \right]$4. for $j = 1;j \le J;j + + $ do 5. 根据式(18)从$\Pr $中提取卸载决策${{{v}}^j}$ 6. 执行计算资源调度:初始化参数${\chi ^{\min }} = \max \{ {S_m}\} ,\,{\chi ^{\max } } = $
$ \displaystyle\sum\limits_m {\left( {\frac{ { {C_m}p_m^{ {\rm{id} } }M} }{ { {F^{ {\rm{fog} } } } } } + {S_m} } \right)}$,于是有${\chi ^{\min }} \le {\chi ^{{\rm{opt}}}} \le {\chi ^{\max }}$,最大
可容忍误差$\varepsilon > 0$, ${\chi ^j}{\rm{ = (}}{\chi ^{\min }} + {\chi ^{\max }}{\rm{)/2}}$7. while $|{\chi ^{\max }} - {\chi ^{\min }}| \ge \varepsilon $ do
8. if $\displaystyle\sum\limits_{m \in M} {\frac{ { {C_m}p_m^{ {\rm{id} } } }}{ { {\chi ^j} - {S_m} } } > {F^{ {\rm{fog} } } }}$ then9. ${\chi ^{\min }} = {\chi ^j}$ 10. else 11. ${\chi ^{\max }} = {\chi ^j}$ 12. end if 13. end while 14. if $|{\chi ^{\max }} - {\chi ^{\min }}| \le \varepsilon $ then 15. ${\chi ^{{\rm{opt}}}} = {\chi ^j}$ 16. end if 17. 将得到的${\chi ^{{\rm{opt}}}}$代入式(21)得到计算资源调度策略${{{f}}^{{\rm{fog}}}}$ 18. end for 表 2 基于在线测量的接入控制算法
1. 初始化每个雾节点的资源块配置数量$z$和剩余资源块数量$B$,
在周期$n$上观察每个雾节点$f$ 的接入请求队列状态$Q_n^f$2. for $f = 1;f < F;f + + $ do 3. 计算$a_{\rm o}^f$,估计${\mathop m\limits^{\wedge} } _{\rm o}^f$ 4. while $Q_n^f \ge B_H^f$ or $B = \emptyset $ do 5. $z \leftarrow z + 1$,${C_f}(n) \leftarrow z\mathop r\limits^\_ $,$B \leftarrow B - 1$ 6. end while 7. 计算$a_{\rm o}^f$及$\hat m_{\rm o}^f$ 8. if $Q_n^f < B_H^f$ & $\hat m_{\rm o}^f \ge a_{\rm o}^f$ then 9. $z \leftarrow z + {\Delta _1}$,${C_f}(n) \leftarrow z\mathop r\limits^\_ $,$B \leftarrow B - {\Delta _1}$ 10. else if $Q_n^f < B_H^f$ & $\hat m_{\rm o}^f \ge a_{\rm o}^f$ then 11. 式(24)执行黄金分割搜索算法估计$\hat P_{n + N}^f$ 12. if $\hat P_{n + N}^f \ge {\varepsilon _f}$ then 13. $z \leftarrow z + {\Delta _2}$, ${C_f}(n) \leftarrow z\mathop r\limits^\_ $, $B \leftarrow B - {\Delta _2}$ 14. end if 15. end if 16. end if 17. end for 表 3 基于迭代的带宽和功率资源调度
1. 初始化迭代次数${N_1}{\rm{ = }}0$和${N_2}{\rm{ = }}0$,误差精度${\delta _1}$和${\delta _2}$, ${V^{{N_1}}}{\rm{ = }}1$ 2. while ${N_1} < {N_{1\max }}$ do 3. while ${N_2} < {N_{2\max }}$ do 4. 对给定的${V^{{N_1}}}$,根据式(31)求得优化的传输功率解 5. 在区间$[0,1]$内执行二分搜索方法求解${\varphi _m}({N_2})$,并将
${\varphi _m}({N_2})$代入式(34)求解带宽资源调度方案6. 通过次梯度法分别更新拉格朗日乘子 7. if ${\rm{||}}\beta ({N_2} + 1) - \beta ({N_2})|{|_2} < {\delta _2}$,
$||\eta ({N_2} + 1) - \eta ({N_2})|{|_2} < {\delta _2}$,
$||\mu ({N_2} + 1) - \mu ({N_2})|{|_2} < {\delta _2}$,
$||\pi ({N_2} + 1) - \pi ({N_2})|{|_2} < {\delta _2}$ then8. $\alpha _m^{{N_1}} = {\alpha _m}({N_2})$, $p_m^{{\rm{com}}{{\rm{N}}_1}} = p_m^{{\rm{com}}}\left( {{N_2}} \right)$, break 9. else 10. ${N_2} = {N_2} + 1$ 11. end if 12. end while 13. if $\left| { {D_m}p_m^{ {\rm{com} }{ {\rm{N} }_{\rm{1} } } } - {V^{ {N_1} } }\alpha _m^{ {N_1} }\lg \left( {1 + \dfrac{ {p_m^{ {\rm{com} }{ {\rm{N} }_{\rm{1} } } }{h_m} } }{ {\alpha _m^{ {N_1} }{N_0}{B_{ {\rm{SC} } } } } } } \right)} \right| < {\delta _1}$ then 14. $\{ {{{p}}^*},{{{\alpha}} ^*}\} = \{ {{{p}}^{{\rm{com}}{{\rm{N}}_{\rm{1}}}}},{{{\alpha}} ^{{N_1}}}\} $ 15. else 16. 令${V^{ {N_1} + 1} } \!\!=\! {D_m}p_m^{ {\rm{com} }{ {\rm{N} }_{\rm{1} } } }/\alpha _m^{ {N_1} }{B_{ {\rm{SC} } } }\lg \!\left( {1 \!+\! \dfrac{ {p_m^{ {\rm{com} }{ {\rm{N} }_{\rm{1} } } }{h_m} } }{ {\alpha _m^{ {N_1} }{N_0}{B_{ {\rm{SC} } } } } } } \right)$ 17. end if 18. end while 19. 输出无线资源调度优化解${{{p}}^*}$, ${{{\alpha}} ^*}$ 表 4 仿真参数
参数 数值 系统带宽 10 MHz(50PRBs) 路径损耗模型 UrbanMicro(UMi) 最大传输功率 23 dBm 计算资源单价 0.10, 0.15, 0.20 unit/cycle 计算密度 297.62 cycle/bit 链路传输速率 1 Mb/s 参数 数值 卸载业务到达 泊松分布 莱斯因子 6 dB 滑动窗口大小 60 ms 平滑指数 0.7 雾计算资源量 1 G cycle 云层计算能力 2 G cycle/s 参数 数值 比特到达速率 0.4 Mbit/ms 噪声功率 –174 dBm/Hz PRB单价 1, 1.5, 2 unit/PRB 仿真时间 6000 ms 队列上溢概率 0.2 单位$t$功率消耗 0.01 W -
MEBREK A, MERGHEM-BOULAHIA L, and ESSEGHIR M. Efficient green solution for a balanced energy consumption and delay in the IoT-Fog-Cloud computing[C]. The 16th IEEE International Symposium on Network Computing and Applications, Cambridge, USA, 2017: 1–4. doi: 10.1109/NCA.2017.8171359. BACCARELLI E, NARANJO P G V, SCARPINITI M, et al. Fog of everything: Energy-efficient networked computing architectures, research challenges, and a case study[J]. IEEE Access, 2017, 5: 9882–9910. doi: 10.1109/ACCESS.2017.2702013 LIU Kaiyang, PENG Jun, ZHANG Xiaoyong, et al. A combinatorial optimization for energy-efficient mobile cloud offloading over cellular networks[C]. 2016 IEEE Global Communications Conference, Washington, USA, 2016: 1–6. doi: 10.1109/GLOCOM.2016.7841488. YANG Lei, CAO Jiannong, TANG Shaojie, et al. A framework for partitioning and execution of data stream applications in mobile cloud computing[C]. The 5th IEEE International Conference on Cloud Computing, Honolulu, USA, 2012: 794–802. doi: 10.1109/CLOUD.2012.97. LIU Mengyu and LIU Yuan. Price-based distributed offloading for mobile-edge computing with computation capacity constraints[J]. IEEE Wireless Communications Letters, 2018, 7(3): 420–423. doi: 10.1109/LWC.2017.2780128 CAO Xiaowen, WANG Feng, XU Jie, et al. Joint computation and communication cooperation for energy-efficient mobile edge computing[J]. IEEE Internet of Things Journal, 2019, 6(3): 4188–4200. doi: 10.1109/JIOT.2018.2875246 MENG Xianling, WANG Wei, and ZHANG Zhaoyang. Delay-constrained hybrid computation offloading with cloud and fog computing[J]. IEEE Access, 2017, 5: 21355–21367. doi: 10.1109/ACCESS.2017.2748140 GU H Y, YANG C Y, and FONG B. Low-complexity centralized joint power and admission control in cognitive radio networks[J]. IEEE Communications Letters, 2009, 13(6): 420–422. doi: 10.1109/LCOMM.2009.082173 JIANG Menglan, CONDOLUCI M, and MAHMOODI T. Network slicing management & prioritization in 5G mobile systems[C]. The 22th European Wireless Conference, Oulu, Finland, 2016: 1–6. YAQOOB S, ULLAH A, AKBAR M, et al. Fog-assisted congestion avoidance scheme for internet of vehicles[C]. The 14th International Wireless Communications & Mobile Computing Conference, Limassol, Cyprus, 2018: 618–622. doi: 10.1109/IWCMC.2018.8450402. LI Jian, PENG Mugen, YU Yuling, et al. Energy-efficient joint congestion control and resource optimization in heterogeneous cloud radio access networks[J]. IEEE Transactions on Vehicular Technology, 2016, 65(12): 9873–9887. doi: 10.1109/TVT.2016.2531184 LIU Yiming, YU F R, LI Xi, et al. Distributed resource allocation and computation offloading in fog and cloud networks with non-orthogonal multiple access[J]. IEEE Transactions on Vehicular Technology, 2018, 67(12): 12137–12151. doi: 10.1109/TVT.2018.2872912 LI Qiuping, ZHAO Junhui, GONG Yi, et al. Energy-efficient computation offloading and resource allocation in fog computing for internet of everything[J]. China Communications, 2019, 16(3): 32–41. SHAHZADI R, NIAZ A, ALI M, et al. Three tier fog networks: Enabling IoT/5G for latency sensitive applications[J]. China Communications, 2019, 16(3): 1–11. SOOKHAK M, YU F R, HE Ying, et al. Fog vehicular computing: Augmentation of fog computing using vehicular cloud computing[J]. IEEE Vehicular Technology Magazine, 2017, 12(3): 55–64. doi: 10.1109/MVT.2017.2667499 LI Di, KAR S, and CUI Shuguang. Distributed quickest detection in sensor networks via two-layer large deviation analysis[J]. IEEE Internet of Things Journal, 2018, 5(2): 930–942. doi: 10.1109/JIOT.2018.2810825 -





 下载:
下载:
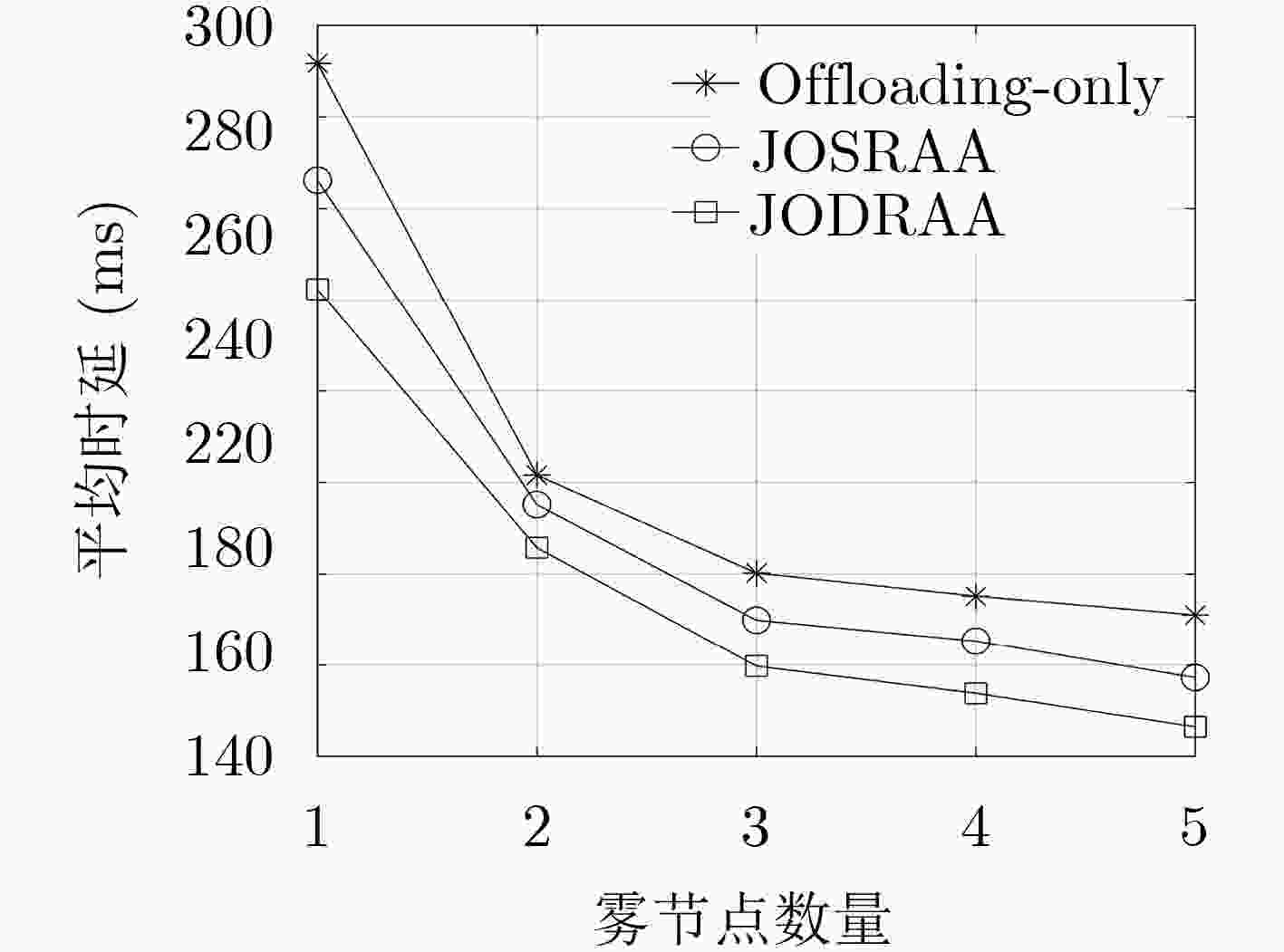
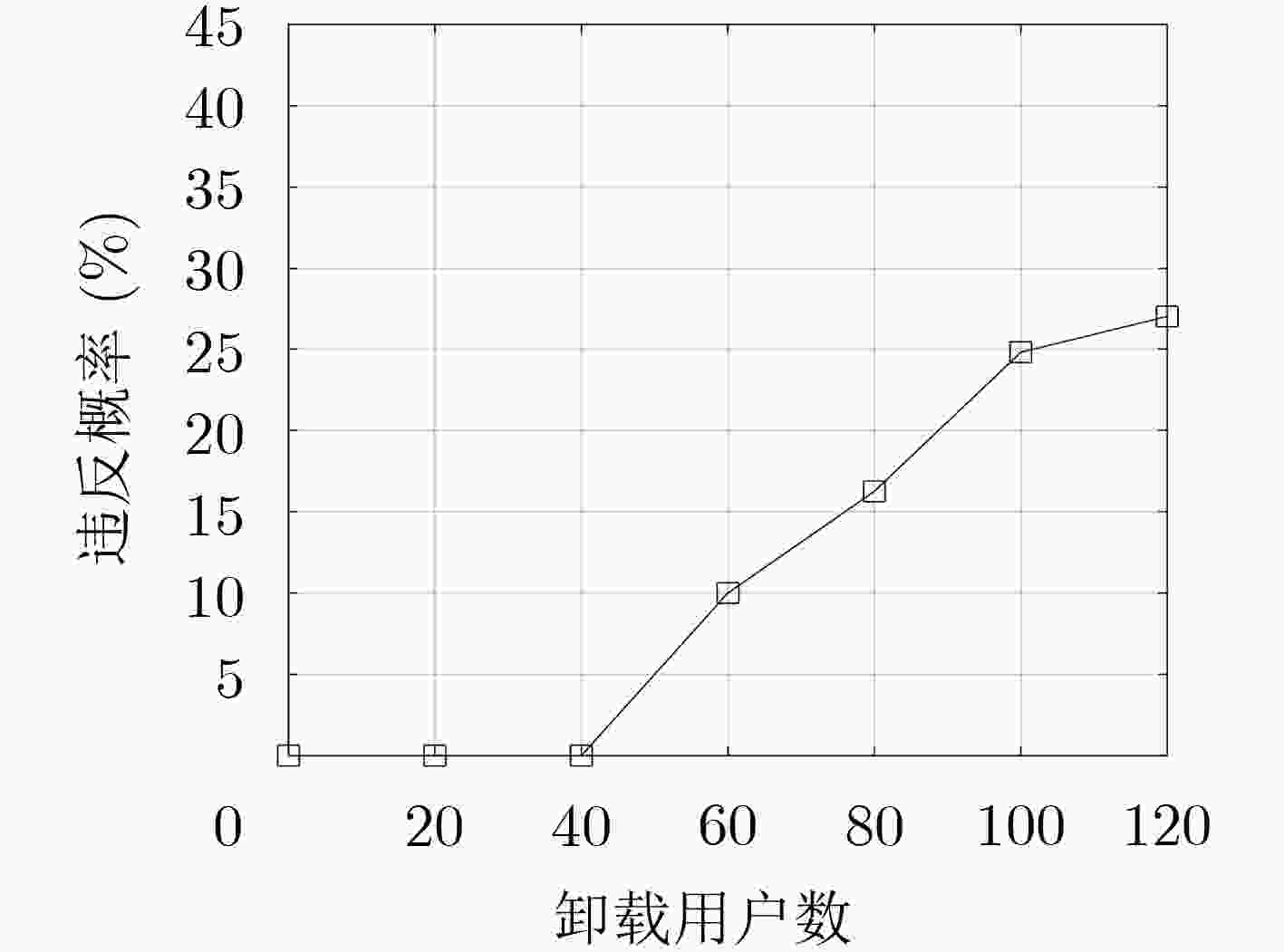


 下载:
下载:
