Virtual Network Function Migration Algorithm Based on Reinforcement Learning for 5G Network Slicing
-
摘要:
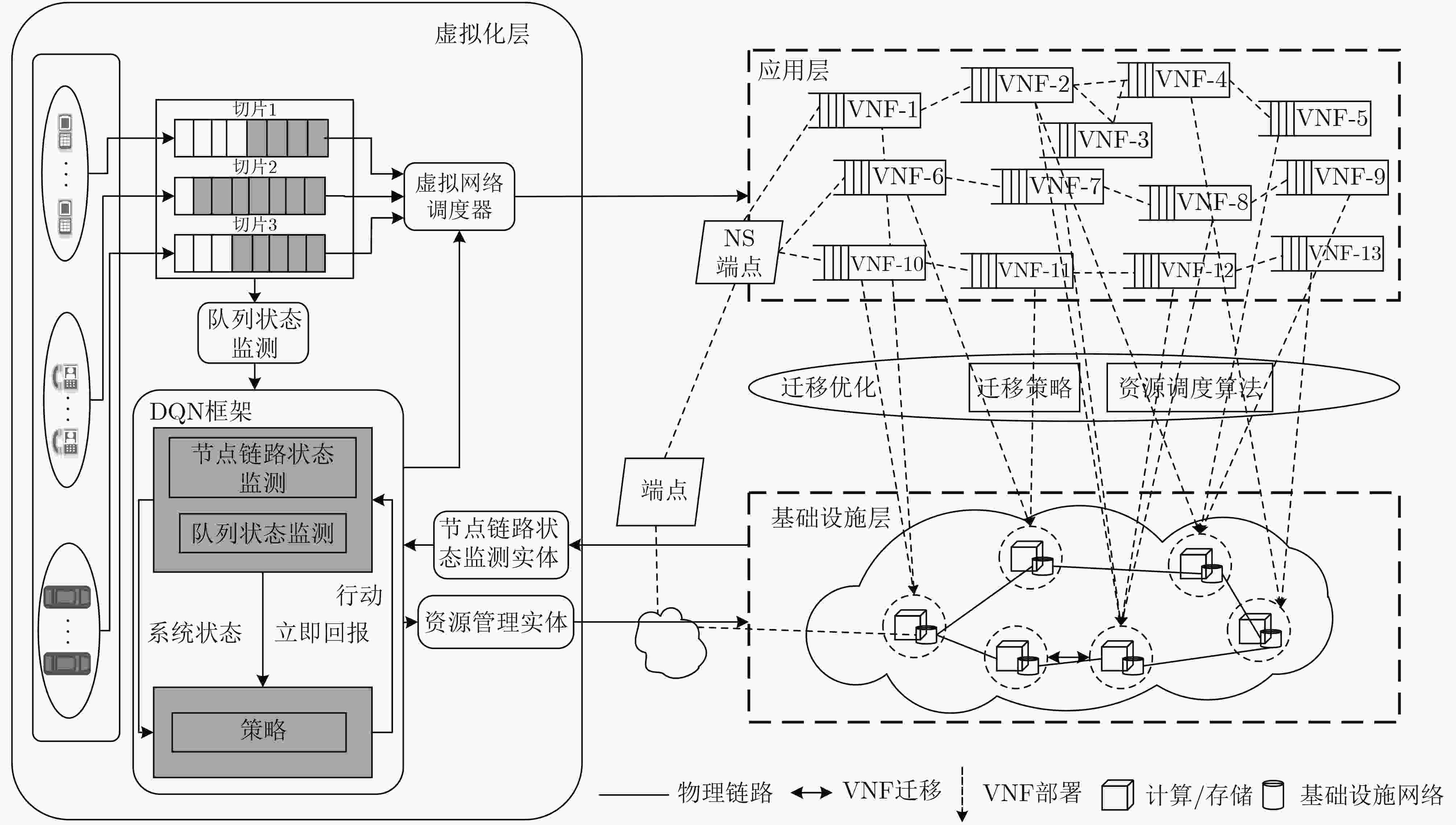
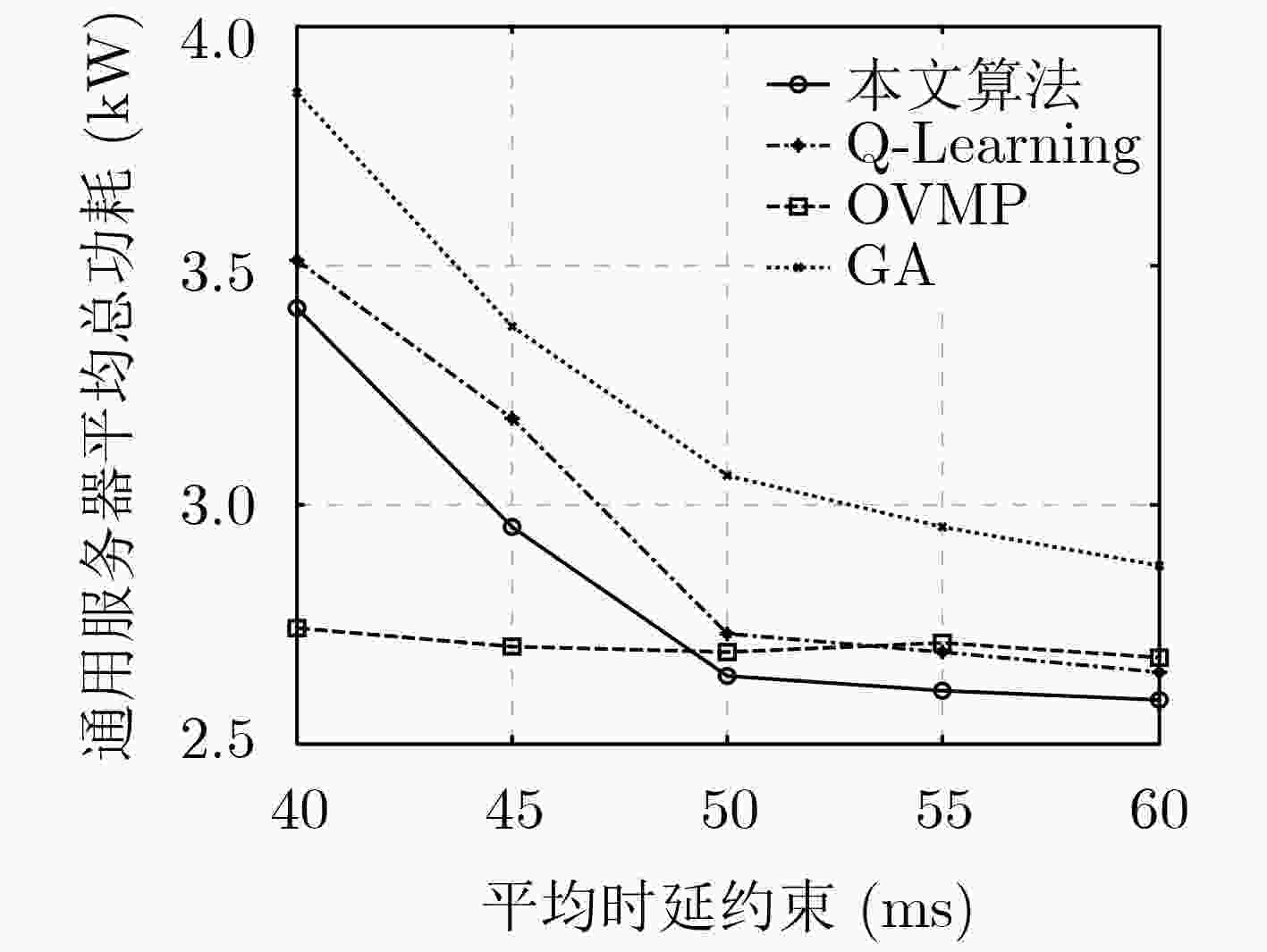
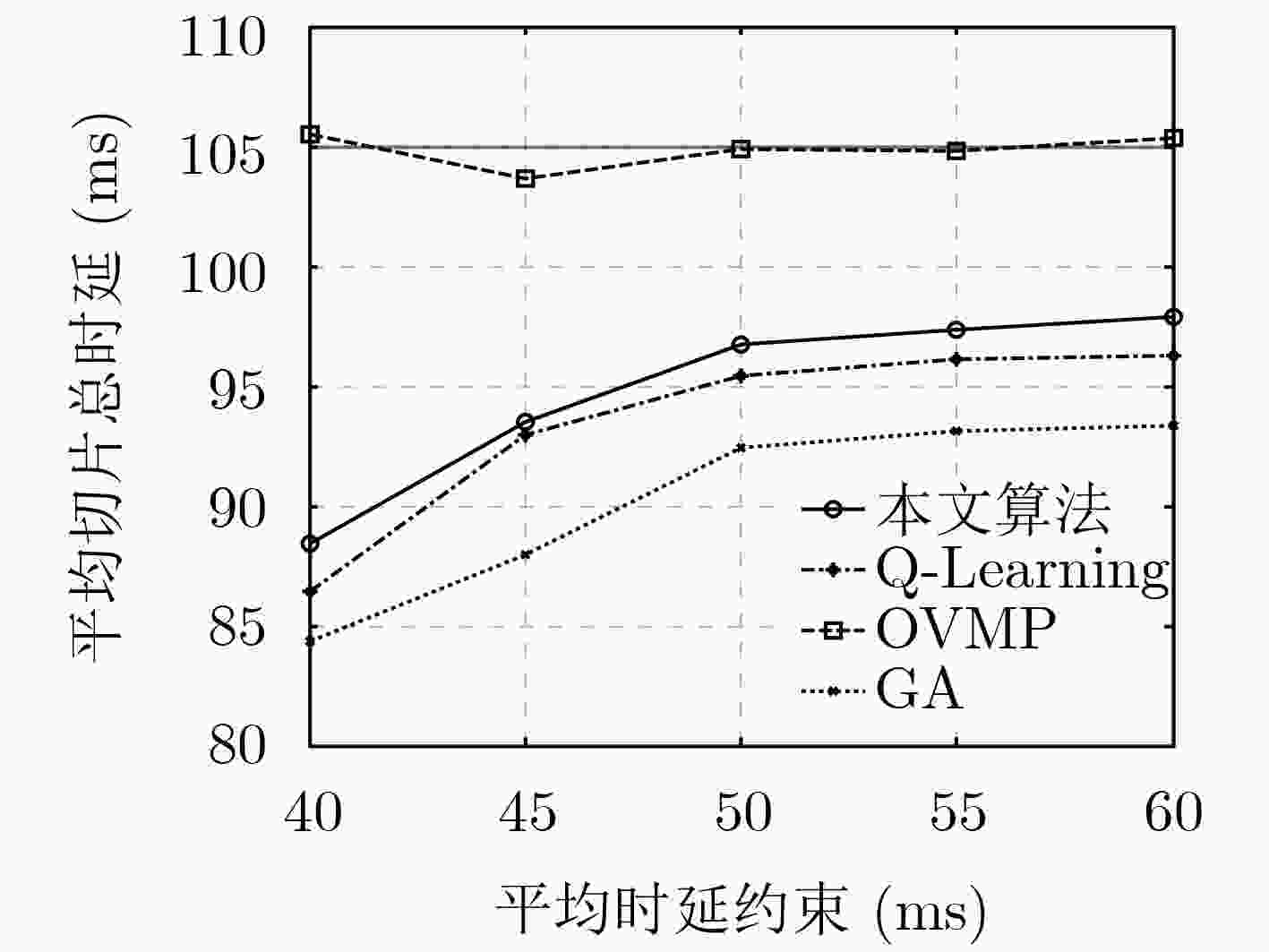
针对5G网络切片架构下业务请求动态性引起的虚拟网络功能(VNF)迁移优化问题,该文首先建立基于受限马尔可夫决策过程(CMDP)的随机优化模型以实现多类型服务功能链(SFC)的动态部署,该模型以最小化通用服务器平均运行能耗为目标,同时受限于各切片平均时延约束以及平均缓存、带宽资源消耗约束。其次,为了克服优化模型中难以准确掌握系统状态转移概率及状态空间过大的问题,该文提出了一种基于强化学习框架的VNF智能迁移学习算法,该算法通过卷积神经网络(CNN)来近似行为值函数,从而在每个离散的时隙内根据当前系统状态为每个网络切片制定合适的VNF迁移策略及CPU资源分配方案。仿真结果表明,所提算法在有效地满足各切片QoS需求的同时,降低了基础设施的平均能耗。
Abstract:In order to solve the Virtual Network Function (VNF) migration optimization problem caused by the dynamicity of service requests on the 5G network slicing architecture, firstly, a stochastic optimization model based on Constrained Markov Decision Process (CMDP) is established to realize the dynamic deployment of multi-type Service Function Chaining (SFC). This model aims to minimize the average sum operating energy consumption of general servers, and is subject to the average delay constraint for each slicing as well as the average cache, bandwidth resource consumption constraints. Secondly, in order to overcome the issue of having difficulties in acquiring the accurate transition probabilities of the system states and the excessive state space in the optimization model, a VNF intelligent migration learning algorithm based on reinforcement learning framework is proposed. The algorithm approximates the behavior value function by Convolutional Neural Network (CNN), so as to formulate a suitable VNF migration strategy and CPU resource allocation scheme for each network slicing according to the current system state in each discrete time slot. The simulation results show that the proposed algorithm can effectively meet the QoS requirements of each slice while reducing the average energy consumption of the infrastructure.
-
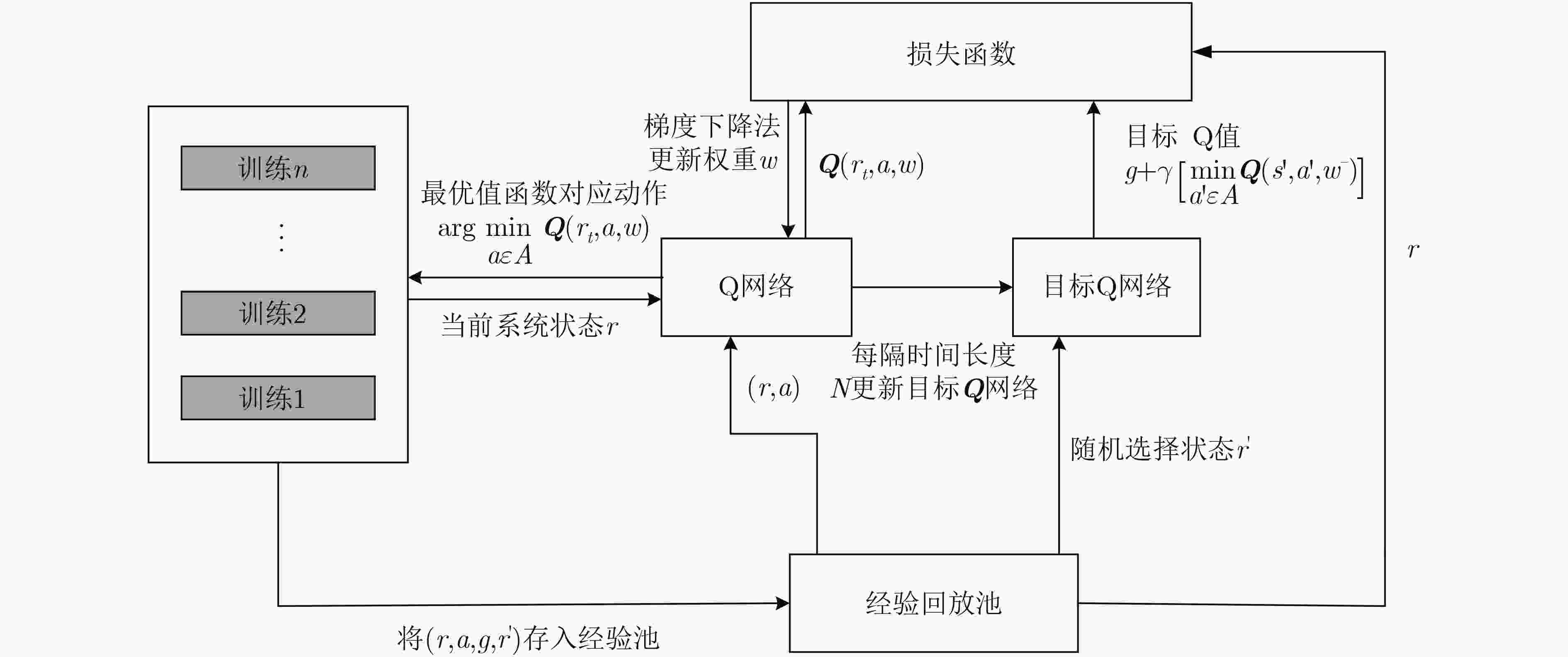
表 1 基于DQN的价值函数近似
(1) 初始化Q网络,采用Xavier[14]初始化权重,即令权重的概率分布函数服从$W \sim U\left[ { - \dfrac{ {\sqrt 6 } }{ {\sqrt { {\upsilon _l} + {\upsilon _{l + 1} } } } },\dfrac{ {\sqrt 6 } }{ {\sqrt { {\upsilon _l} + {\upsilon _{l + 1} } } } } } \right]$的均匀分布,初始化目
标Q网络,权重为${w^ - } = w$,其中$l$为网络层数,$\upsilon $为神经元个数(2) 初始化拉格朗日乘子$\beta _i^d \leftarrow 0,\beta _h^q \leftarrow 0,\beta _{h,l}^x \leftarrow 0,$$\forall i \in I,\forall h,l \in H$,初始化经验回放池 (3) for episode $k = 1,2, ···,K$ do (4) 随机选取一个状态初始化${r_1}$ (5) for $t = 1,2, ···,T$ do (6) 随机选择一个概率$p$,if $p \ge \varepsilon $ (7) 计算VNF迁移及CPU资源分配策略$a_t^{\rm{*} } = \arg \mathop {\min }\limits_{a \in A} { Q}({r_t},a,w)$ (8) else 选择一个随机的行动${a_t} \ne a_t^{\rm{*}}$ (9) 执行行动${a_t}$,获得拉格朗日回报${g^\beta }({r_t},{a_t})$,并观察下一时刻状态${r_{t + 1}}$ (10) 将经验样本$\left( {{r_t},{a_t},{g^\beta }({r_t},{a_t}),{r_{t + 1}}} \right)$存入经验回放池中 (11) 从经验池中随机抽取一组Mini-batch的经验样本$\left( {{r_k},{a_k},{g^\beta }({r_k},{a_k}),{r_{k + 1}}} \right)$ (12) 利用目标Q网络得到$\mathop {\min }\limits_{ {a'} \in A} { Q}({r_{t + 1} },{a'},{w^ - })$,求得${y_k} = {g^\beta }({r_k},{a_k}) + \gamma \mathop {\min }\limits_{ {a'} \in A} { Q}({r_{t + 1} },{a'},{w^ - })$ (13) 对${\left( { {y_k} - { Q}({r_t},{a_k},w)} \right)^2}$使用梯度下降法对$w$进行更新 (14) 每隔时间长度${T_q}$更新目标Q网络,即${w^ - } = w$ (15) 利用随机次梯度法更新拉格朗日乘子${ \beta} :\beta \ge 0$ (16) end for (17) end for 表 2 基于DQN的VNF在线迁移算法
(1) for $t = 1,2,···,T$ do (2) \*网络状态的监测*\ (3) 监测当前时隙$t$下的全局状态$r(t)$,包括全局队列状态${{Q}}({{t}})$、全局节点状态${{\zeta}} ({{t}})$以及全局链路状态${{\eta}} ({{t}})$ (4) if ${\zeta _h}(t) = 0{\text{或}}{\eta _{h,l} }(t) = 0$ (5) 在将满足$B(h,f) = 1{\text{或}}P({f_p}|{f_j})B({f_j},h)B({f_p},l) \ne 0$的所有$\forall f \in F$迁移至其它节点的基础上,计算最优的VNF迁移策略及
CPU资源分配策略$a_t^{\rm{*} } = \arg \mathop {\min }\limits_{a \in A} { Q}({r_t},a,w)$(6) else (7) 直接计算最优的VNF迁移策略及CPU资源分配策略$a_t^{\rm{*} } = \arg \mathop {\min }\limits_{a \in A} { Q}({r_t},a,w)$ (8) 基于最优行动$a_t^{\rm{*}}$执行VNF的迁移,并进行资源的分配 (9) $t = t + 1$ (10) end for 表 3 仿真参数
仿真参数 仿真值 仿真参数 仿真值 网络切片业务数量$I$ 3 服务器总台数$H$ 8 VNF种类$J$ 10 节点失效率 服从均值为[0.01,0.02]均匀分布 时隙长度${T_s} $ 10 s 链路失效率 服从均值为[0.02,0.04]均匀分布 数据包到达过程 独立同分布的泊松过程 链路传输时延$\delta $ 0.5 ms 平均数据包大小$\overline P$ 500 kbit/packet 服务器最高功率$P_h$ 800 W 节点缓存空间$\chi $ 300 MB 服务器功耗百分比$u_h$ 0.3 节点CPU个数$\kappa $ 8 最大迭代轮数 2000 单个CPU最大服务速率$\xi $ 25 MB/s 总训练步长 200000 链路带宽容量Δ 640 Mbps 学习率$\alpha $ 0.0001 折扣因子$\gamma $ 0.9 Mini-batch 8 表 4 CNN神经网络参数
网络层 卷积核大小 卷积步长 卷积核个数 激活函数 卷积层1 $7 \times 7$ 2 32 ReLU 卷积层2 $5 \times 5$ 2 64 ReLU 卷积层3 $3 \times 3$ 1 64 ReLU 全连接层1 – – 512 ReLU 全连接层2 – – 122 Linear -
GE Xiaohu, TU Song, MAO Guoqiang, et al. 5G ultra-dense cellular networks[J]. IEEE Wireless Communications, 2016, 23(1): 72–79. doi: 10.1109/mwc.2016.7422408 SUGISONO K, FUKUOKA A, and YAMAZAKI H. Migration for VNF instances forming service chain[C]. The 7th IEEE International Conference on Cloud Networking, Tokyo, Japan, 2018: 1–3. doi: 10.1109/CloudNet.2018.8549194. ZHENG Qinghua, LI Rui, LI Xiuqi, et al. Virtual machine consolidated placement based on multi-objective biogeography-based optimization[J]. Future Generation Computer Systems, 2016, 54: 95–122. doi: 10.1016/j.future.2015.02.010 ZHANG Xiaoqing, YUE Qiang, and HE Zhongtang. Dynamic Energy-efficient Virtual Machine Placement Optimization for Virtualized Clouds[M]. JIA Limin, LIU Zhigang, QIN Yong, et al. Proceedings of the 2013 International Conference on Electrical and Information Technologies for Rail Transportation (EITRT2013)-Volume II. Berlin, Heidelberg: Springer, 2014, 288: 439–448. doi: 10.1007/978-3-642-53751-6_47. ERAMO V, AMMAR M, and LAVACCA F G. Migration energy aware reconfigurations of virtual network function instances in NFV architectures[J]. IEEE Access, 2017, 5: 4927–4938. doi: 10.1109/ACCESS.2017.2685437 ERAMO V, MIUCCI E, AMMAR M, et al. An approach for service function chain routing and virtual function network instance migration in network function virtualization architectures[J]. IEEE/ACM Transactions on Networking, 2017, 25(4): 2008–2025. doi: 10.1109/TNET.2017.2668470 WEN Tao, YU Hongfang, SUN Gang, et al. Network function consolidation in service function chaining orchestration[C]. 2016 IEEE International Conference on Communications, Kuala Lumpur, Malaysia, 2016: 1–6. doi: 10.1109/ICC.2016.7510679. YANG Jian, ZHANG Shuben, WU Xiaomin, et al. Online learning-based server provisioning for electricity cost reduction in data center[J]. IEEE Transactions on Control Systems Technology, 2017, 25(3): 1044–1051. doi: 10.1109/TCST.2016.2575801 CHENG Aolin, LI Jian, YU Yuling, et al. Delay-sensitive user scheduling and power control in heterogeneous networks[J]. IET Networks, 2015, 4(3): 175–184. doi: 10.1049/iet-net.2014.0026 LI Rongpeng, ZHAO Zhifeng, CHEN Xianfu, et al. TACT: A transfer actor-critic learning framework for energy saving in cellular radio access networks[J]. IEEE Transactions on Wireless Communications, 2014, 13(4): 2000–2011. doi: 10.1109/TWC.2014.022014.130840 WANG Shangxing, LIU Hanpeng, GOMES P H, et al. Deep reinforcement learning for dynamic multichannel access in wireless networks[J]. IEEE Transactions on Cognitive Communications and Networking, 2018, 4(2): 257–265. doi: 10.1109/TCCN.2018.2809722 HUANG Xiaohong, YUAN Tingting, QIAO Guanghua, et al. Deep reinforcement learning for multimedia traffic control in software defined networking[J]. IEEE Network, 2018, 32(6): 35–41. doi: 10.1109/MNET.2018.1800097 HE Ying, ZHANG Zheng, YU F R, et al. Deep-reinforcement-learning-based optimization for cache-enabled opportunistic interference alignment wireless networks[J]. IEEE Transactions on Vehicular Technology, 2017, 66(11): 10433–10445. doi: 10.1109/TVT.2017.2751641 GLOROT X and BENGIO Y. Understanding the difficulty of training deep feedforward neural networks[C]. The International Conference on Artificial Intelligence and Statistics, Sardinia, 2010: 249–256. PERUMAL V and SUBBIAH S. Power-conservative server consolidation based resource management in cloud[J]. International Journal of Network Management, 2014, 24(6): 415–432. doi: 10.1002/nem.1873 QU Long, ASSI C, SHABAN K, et al. Delay-aware scheduling and resource optimization with network function virtualization[J]. IEEE Transactions on Communications, 2016, 64(9): 3746–3758. doi: 10.1109/TCOMM.2016.2580150 -





 下载:
下载:


 下载:
下载:
