Network Traffic Anomaly Detection Method Based on Deep Features Learning
-
摘要:
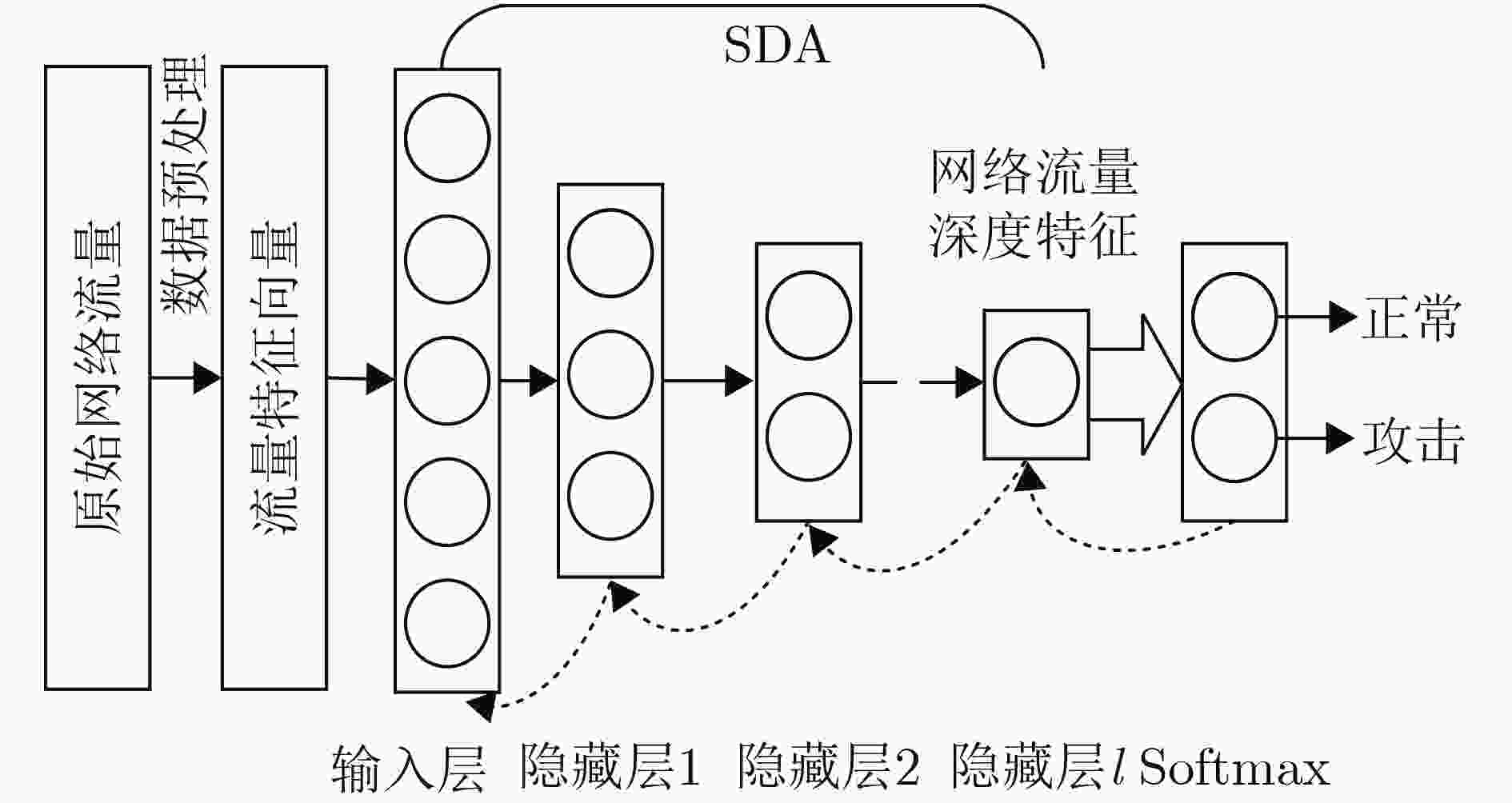
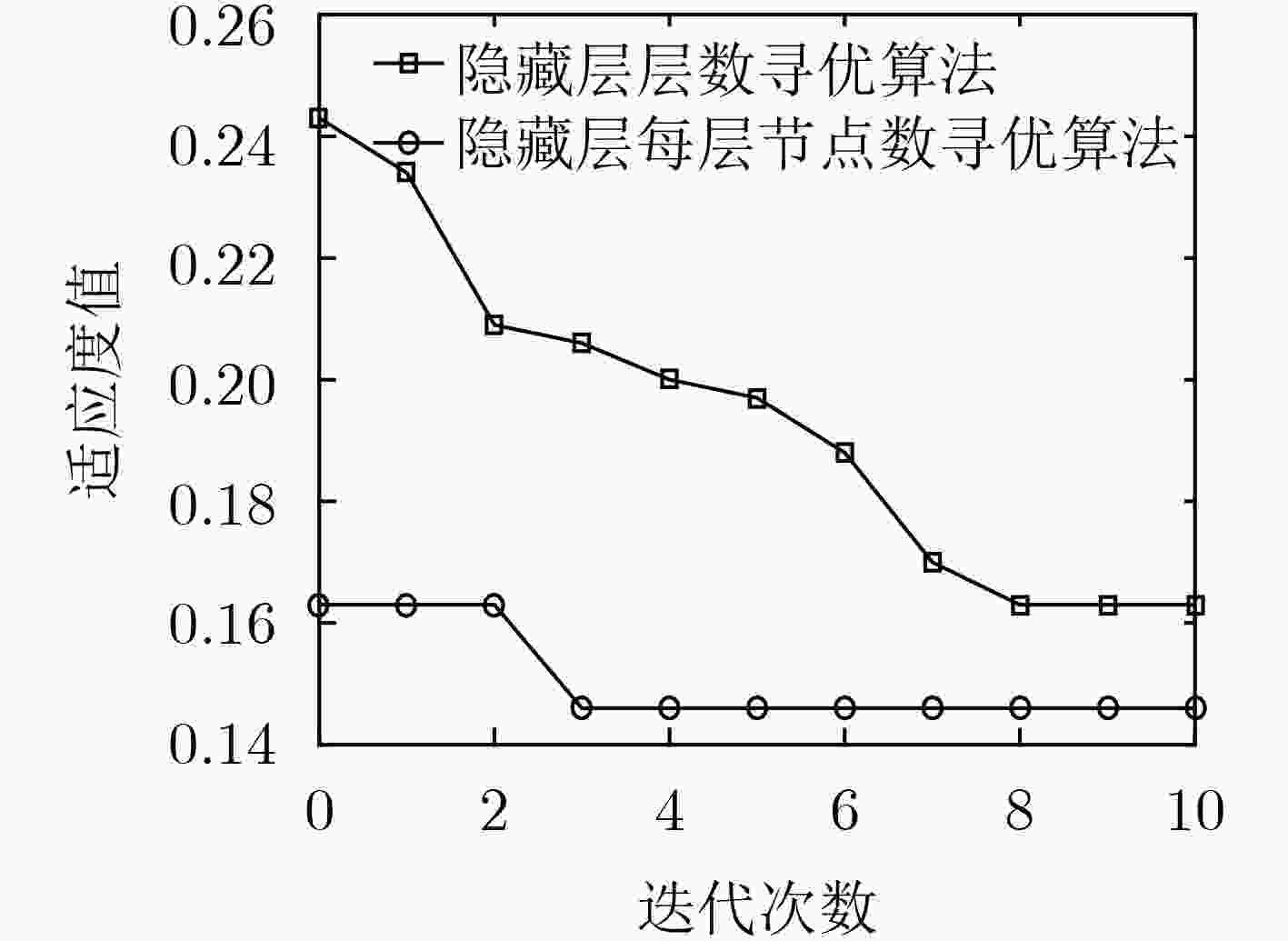
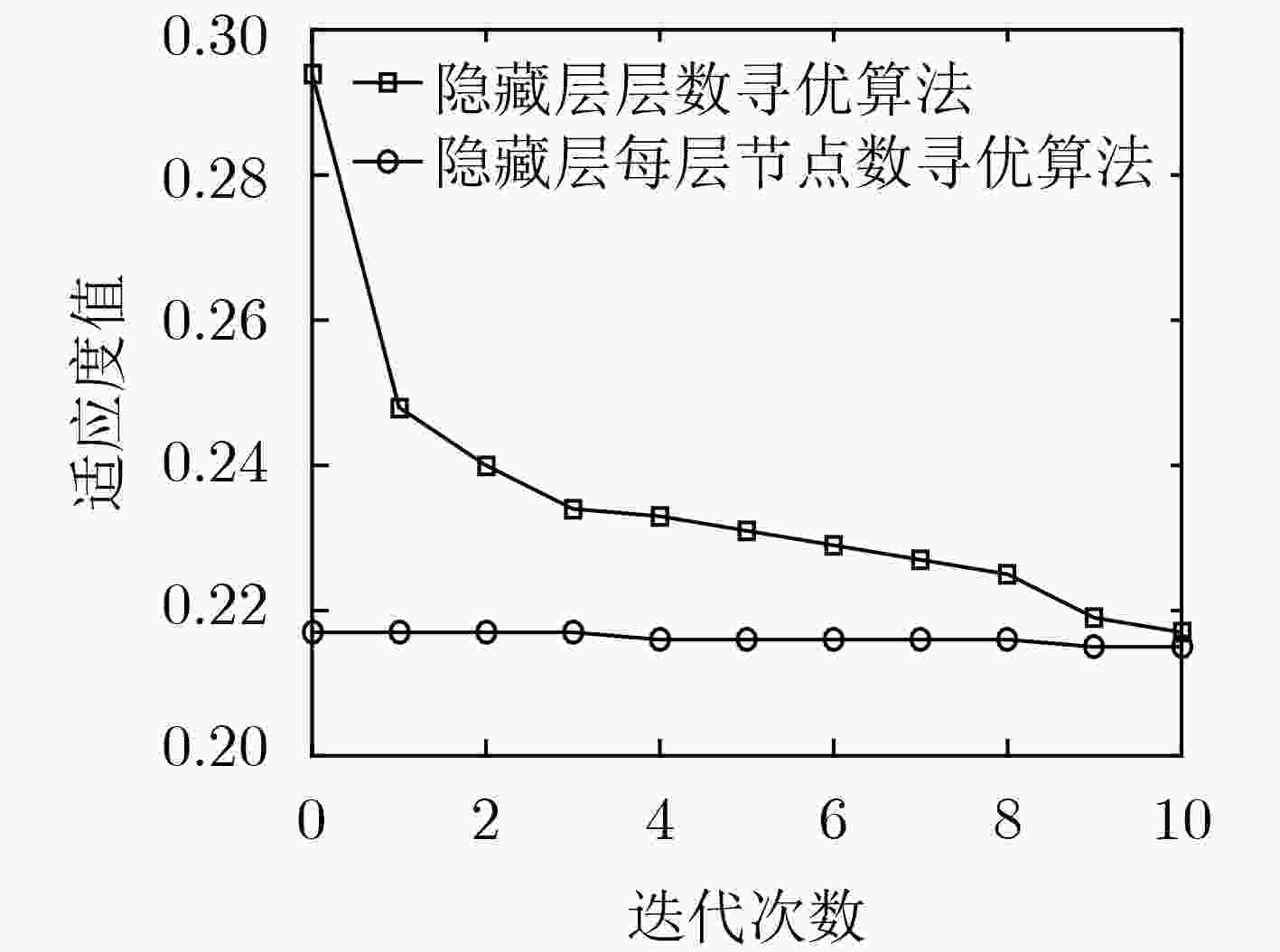
针对网络流量异常检测过程中提取的流量特征准确性低、鲁棒性差导致流量攻击检测率低、误报率高等问题,该文结合堆叠降噪自编码器(SDA)和softmax,提出一种基于深度特征学习的网络流量异常检测方法。首先基于粒子群优化算法设计SDA结构两阶段寻优算法:根据流量检测准确率依次对隐藏层层数及每层节点数进行寻优,确定搜索空间中的最优SDA结构,从而提高SDA提取特征的准确性。然后采用小批量梯度下降算法对优化的SDA进行训练,通过最小化含噪数据重构向量与原始输入向量间的差异,提取具有较强鲁棒性的流量特征。最后基于提取的流量特征对softmax进行训练构建异常检测分类器,从而实现对流量攻击的高性能检测。实验结果表明:该文所提方法可根据实验数据及其分类任务动态调整SDA结构,提取的流量特征具有更高的准确性和鲁棒性,流量攻击检测率高、误报率低。
Abstract:In view of the problems of low attack detection rate and high false positive rate caused by poor accuracy and robustness of the extracted traffic features in network traffic anomaly detection, a network traffic anomaly detection method based on deep features learning is proposed, which is combined with Stacked Denoising Autoencoders (SDA) and softmax. Firstly, a two-stage optimization algorithm is designed based on particle swarm optimization algorithm to optimize the structure of SDA, the number of hidden layers and nodes in each layer is optimized successively based on the traffic detection accuracy, and the optimal structure of SDA in the search space is determined, improving the accuracy of traffic features extracted by SDA. Secondly, the optimized SDA is trained by the mini-batch gradient descent algorithm, and the traffic features with strong robustness are extracted by minimizing the difference between the reconstruction vector of the corrupted data and the original input vector. Finally, softmax is trained by the extracted traffic features to construct an anomaly detection classifier for detecting traffic attacks with high performance. The experimental results show that the proposed method can adjust the structure of SDA based on the experimental data and its classification tasks, extract traffic features with a higher accuracy and robustness, and detect traffic attacks with high detection rate and low false positive rate.
-
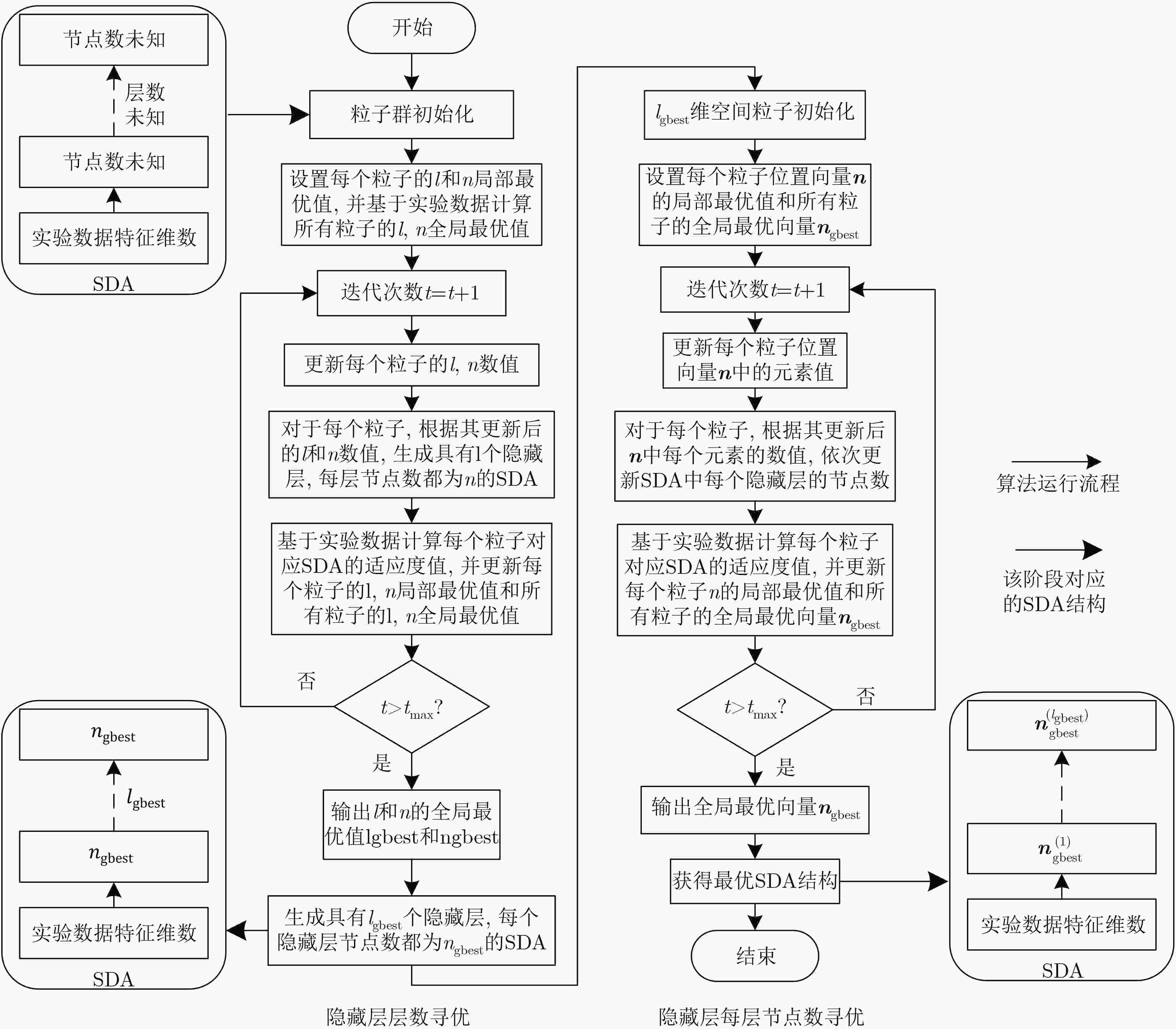
表 1 隐藏层层数寻优算法
输入:流量异常检测数据集,NP,${t_{\max }}$, $w$, ${c_1}$, ${c_2}$, ${l_{\max }}$, ${l_{\min }}$, ${v_{l,\max }}$, ${v_{l,\min }}$, ${n_{\max }}$, ${n_{\min }}$, ${v_{n,\max }}$, ${v_{n,\min }}$ 输出:具有${l_{{\rm{gbest}}}}$个隐藏层且每层节点数为${n_{{\rm{gbest}}}}$的SDA for $i = 1\;{\rm{to}}\;{{\rm{NP}}}$ do 采用式(5)—式(8)对粒子群进行初始化,并分别将${l_{i,{\rm{pbest}}}}$和${n_{i,{\rm{pbest}}}}$初始化为${l_i}(0)$和${n_i}(0)$; 基于实验数据,采用式(9)计算粒子i的适应度值; 将最小适应度值对应的l和n设置为${l_{{\rm{gbest}}}}$和${n_{{\rm{gbest}}}}$初始化值; for $t = {1_{}}{\rm{t}}{{\rm{o}}_{}}\begin{array}{*{20}{c}} {{t_{\max }}} \end{array}$ do for $i = {1_{}}{\rm{t}}{{\rm{o}}_{}}\begin{array}{*{20}{c}} {{\rm{NP}}} \end{array}$ do 采用式(1)—式(4)更新粒子i的${l_i}(t)$速度和数值,以及${n_i}(t)$的速度和数值; if ${v_{{l_i}}}(t)$, ${l_i}(t)$,${v_{{n_i}}}(t)$ or ${n_i}(t)$超过其搜索范围 对${v_{{l_i}}}(t)$, ${l_i}(t)$,${v_{{n_i}}}(t)$ or ${n_i}(t)$再次进行随机初始化; 生成具有${l_i}(t)$个隐藏层且每层节点数为${n_i}(t)$的SDA; 基于实验数据,采用式(9)计算粒子i的适应度值; if(${\rm{fit} } ({l_i}(t),{n_i}(t)) < {\rm{fit} } ({l_{i,{\rm pbest}} },{n_{i,{\rm{pbest} } } })$)//若粒子i的适应度值小于局部最优值对应的适应度值,则对局部最优值进行更新 分别将${l_i}(t)$和${n_i}(t)$赋值给${l_{i,{\rm{pbest}}}}$和${n_{i,{\rm{pbest}}}}$; if(${\rm{fit}} ({l_i}(t),{n_i}(t)) < {\rm{fit}} ({l_{{\rm{gbest}}}},{n_{{\rm{gbest}}}})$)//若粒子i的适应度值小于全局最优值对应的适应度值,则对全局最优值进行更新 分别将${l_i}(t)$和${n_i}(t)$赋值给${l_{{\rm{gbest}}}}$和${n_{{\rm{gbest}}}}$; 迭代结束后,生成具有${l_{{\rm{gbest}}}}$个隐藏层且每层节点数为${n_{{\rm{gbest}}}}$的SDA; return 具有${l_{{\rm{gbest}}}}$个隐藏层且每层节点数为${n_{{\rm{gbest}}}}$的SDA。 表 2 隐藏层每层节点数寻优算法
输入:流量异常检测数据集,NP, ${t_{\max }}$, $w$, ${c_1}$, ${c_2}$, ${v_{\max }}$, ${v_{\min }}$, ${l_{{\rm{gbest}}}}$, ${n_{{\rm{gbest}}}}$ 输出:最优SDA结构 for $i = {1 }\ {\rm{t} }{ {\rm{o} }_{} }\ { {\rm{NP} } } $ do for $h = {1_{} }\ {\rm{t} }{ {\rm{o} }_{} }\ {l_{ {\rm{gbest} } } }$ do 初始化粒子位置$n_i^{(h)}(0) = {n_{{\rm{gbest}}}}$,采用式(12)初始化粒子速度,并将局部最优向量${{{n}}_{i,{\rm{pbest}}}}$中的$n_{i,{\rm{pbest}}}^{(h)}$初始化为${n_{{\rm{gbest}}}}$; 设置全局最优向量${ {{n} }_{ {\rm{gbest} } } } = \min \{ { {{n} }_{ {\rm{1,pbest} } } },{ {{n} }_{ {\rm{2,pbest} } } }, ··· ,{ {{n} }_{ {\rm{NP,pbest} } } }\} = {[{n_{ {\rm{gbest} } } }_{}{n_{ {\rm{gbest} } } } ··· {n_{ {\rm{gbest} } } }]^{\rm T}}$; for $t = {1_{}}{\rm{t}}{{\rm{o}}_{}}\begin{array}{*{20}{c}} {{t_{\max }}} \end{array}$ do for $i = {1_{}}{\rm{t}}{{\rm{o}}_{}}\begin{array}{*{20}{c}} {{\rm{NP}}} \end{array}$ do for $h = {1_{}}{\rm{t}}{{\rm{o}}_{}}{l_{{\rm{gbest}}}}$ do 采用式(10)和式(11)更新粒子i位置向量${{{n}}_i}(t)$中元素$n_i^{(h)}(t)$的速度和数值; if $v_i^{(h)}(t)$ or $n_i^{(h)}(t)$超过其搜索范围 对$v_i^{(h)}(t)$ or $n_i^{(h)}(t)$再次进行随机初始化; 根据更新后的${{{n}}_i}(t)$,将SDA每个隐藏层的节点数分别更新为$n_i^{(1)}(t),n_i^{(2)}(t), ··· ,n_i^{({l_{{\rm{gbest}}}})}(t)$; 基于实验数据,采用式(13)计算粒子i的适应度值; if(${\rm{fit}} ({{{n}}_i}(t)) < {\rm{fit}} ({{{n}}_{i,{\rm{pbest}}}})$)//若粒子i的适应度值小于局部最优向量对应的适应度值,则对局部最优向量进行更新 ${{{n}}_{i,{\rm{pbest}}}} \leftarrow {{{n}}_i}(t)$; ${{{n}}_{{\rm{gbest}}}} \leftarrow \min \{ {{{n}}_{{\rm{1,pbest}}}},{{{n}}_{{\rm{2,pbest}}}}, ··· ,{{{n}}_{{\rm{NP,pbest}}}}\} $;//采用局部最优向量中的最小值更新全局最优向量 迭代结束后,根据最终${{{n}}_{{\rm{gbest}}}}$分别将SDA的隐藏层每层节点数更新为$n_{{\rm{gbest}}}^{(1)},n_{{\rm{gbest}}}^{(2)}, ··· ,n_{{\rm{gbest}}}^{({l_{{\rm{pbest}}}})}$; return 最优SDA结构。 表 3 二分类场景不同模型检测性能
模型类型 基于SAE的异常
检测模型基于传统SDA的
异常检测模型基于一阶段寻优SDA的
异常检测模型基于两阶段寻优SDA的
异常检测模型模型结构 [28, 3, 2, 2, 2, 1, 3, 3, 3, 2] [28, 28, 28, 28, 2] [28, 2, 2, 2, 2, 2, 2, 2, 2, 2] [28, 3, 2, 2, 2, 1, 3, 3, 3, 2] Acc (%) 86.29 86.52 86.58 92.68 DR (%) 92.85 96.10 94.75 96.80 Rec (%) 90.04 92.68 89.26 94.48 FPR (%) 4.96 3.38 3.51 2.72 ${T_{{\rm{tr}}}}$(m) 8.24 8.52 7.45 8.50 ${T_{{\rm{te}}}}$(s) 0.18 0.18 0.18 0.18 表 4 多分类场景不同模型检测性能
模型类型 基于SAE的异常
检测模型基于传统SDA的
异常检测模型基于一阶段寻优SDA的
异常检测模型基于两阶段寻优SDA的
异常检测模型模型结构 [28, 24, 5] [28, 28, 28, 28, 5] [28, 25, 5] [28, 24, 5] Acc (%) 84.12 84.31 84.96 85.37 Normal DR (%) 84.58 85.37 85.87 86.34 Rec (%) 96.74 96.88 97.01 97.28 FPR (%) 17.98 18.89 18.06 17.25 DoS DR (%) 94.08 94.74 94.92 95.59 Rec (%) 83.65 84.51 82.63 85.88 FPR (%) 2.05 2.04 2.02 1.72 Probe DR (%) 79.42 75.58 79.71 83.27 Rec (%) 65.14 67.29 63.78 68.28 FPR (%) 1.78 2.21 1.70 1.34 R2L DR (%) 90.96 92.06 83.78 90.50 Rec (%) 58.23 60.99 58.34 60.23 FPR (%) 0.27 0.21 0.57 0.30 U2R DR (%) 88.05 28.60 72.58 76.19 Rec (%) 2.50 2.00 4.50 3.00 FPR (%) 0.01 0.03 0.01 0.01 ${T_{{\rm{tr}}}}$(m) 3.94 6.32 6.54 5.36 ${T_{{\rm{te}}}}$(s) 0.20 0.40 0.41 0.26 表 5 多分类场景不同模型检测含噪流量的准确率
模型类型 Acc (%) 0.1 0.2 0.3 基于SAE的异常检测模型 81.57 79.31 76.69 基于传统SDA的异常检测模型 83.63 83.54 83.48 基于一阶段寻优SDA的异常检测模型 84.71 84.52 84.23 基于两阶段寻优SDA的异常检测模型 85.08 85.01 85.02 -
KWON D, KIM H, KIM J, et al. A survey of deep learning-based network anomaly detection[J]. Cluster Computing, 2019, 22(Suppl 1): 949–961. 高妮, 高岭, 贺毅岳, 等. 基于自编码网络特征降维的轻量级入侵检测模型[J]. 电子学报, 2017, 45(3): 730–739. doi: 10.3969/j.issn.0372-2112.2017.03.033GAO Ni, GAO Ling, HE Yiyue, et al. A lightweight intrusion detection model based on autoencoder network with feature reduction[J]. Acta Electronica Sinica, 2017, 45(3): 730–739. doi: 10.3969/j.issn.0372-2112.2017.03.033 ALRAWASHDEH K and PURDY C. Toward an online anomaly intrusion detection system based on deep learning[C]. The 15th IEEE International Conference on Machine Learning and Applications, Anaheim, USA, 2016: 195–200. doi: 10.1109/ICMLA.2016.0040. JAVAID A, NIYAZ Q, SUN Weiqing, et al. A deep learning approach for network intrusion detection system[C]. The 9th EAI International Conference on Bio-inspired Information and Communications Technologies, New York, USA, 2015: 21–26. doi: 10.4108/eai.3-12-2015.2262516. YOUSEFI-AZAR M, VARADHARAJAN V, HAMEY M, et al. Autoencoder-based feature learning for cyber security applications[C]. The 2017 International Joint Conference on Neural Networks, Anchorage, USA, 2017: 3854–3861. doi: 10.1109/IJCNN.2017.7966342. WANG Wei, ZHU Ming, ZENG Xuewen, et al. Malware traffic classification using convolutional neural network for representation learning[C]. 2017 International Conference on Information Networking, Da Nang, Vietnam, 2017: 712–717. doi: 10.1109/ICOIN.2017.7899588. 王勇, 周慧怡, 俸皓, 等. 基于深度卷积神经网络的网络流量分类方法[J]. 通信学报, 2018, 39(1): 14–23. doi: 10.11959/j.issn.1000-436x.2018018WANG Yong, ZHOU Huiyi, FENG Hao, et al. Network traffic classification method basing on CNN[J]. Journal on Communications, 2018, 39(1): 14–23. doi: 10.11959/j.issn.1000-436x.2018018 YU Yang, LONG Jun, and CAI Zhiping. Session-based network intrusion detection using a deep learning architecture[C]. The 14th International Conference on Modeling Decisions for Artificial Intelligence, Kitakyushu, Japan, 2017: 144–155. doi: 10.1007/978-3-319-67422-3_13. VINCENT P, LAROCHELLE H, LAJOIE I, et al. Stacked Denoising Autoencoders: Learning useful representations in a deep network with a local denoising criterion[J]. The Journal of Machine Learning Research, 2010, 11: 3371–3408. Canadian Institute for Cybersecurity. NSL-KDD dataset[EB/OL]. https://www.unb.ca/cic/datasets/nsl.html, 2018. QOLOMANY B, MAABREH M, AL-FUQAHA, et al. Parameters optimization of deep learning models using particle swarm optimization[C]. The 13th International Wireless Communications and Mobile Computing Conference, Valencia, Spain, 2017: 1285–1290. doi: 10.1109/IWCMC.2017.7986470. WANG Yao, CAI Wandong, and WEI Pengcheng. A deep learning approach for detecting malicious JavaScript code[J]. Security and Communication Networks, 2016, 9(11): 1520–1534. doi: 10.1002/sec.1441 陈建廷, 向阳. 深度神经网络训练中梯度不稳定现象研究综述[J]. 软件学报, 2018, 29(7): 2071–2091. doi: 10.13328/j.cnki.jos.005561CHEN Jianting and XIANG Yang. Survey of unstable gradients in deep neural network training[J]. Journal of Software, 2018, 29(7): 2071–2091. doi: 10.13328/j.cnki.jos.005561 谷丛丛, 王艳, 严大虎, 等. 基于自编码组合特征提取的分类方法研究[J]. 系统仿真学报, 2018, 30(11): 4132–4140. doi: 10.16182/j.issn1004731x.joss.201811011GU Congcong, WANG Yan, YAN Dahu, et al. Research on classification based on autoencoder combination features extraction method[J]. Journal of System Simulation, 2018, 30(11): 4132–4140. doi: 10.16182/j.issn1004731x.joss.201811011 FIORE U, PALMIERI F, CASTIGLIONE A, et al. Network anomaly detection with the restricted Boltzmann machine[J]. Neurocomputing, 2013, 122: 13–23. doi: 10.1016/j.neucom.2012.11.050 KINGMA D and BA J. Adam: A method for stochastic optimization[C/OL]. https://arxiv.org/abs/1412.6980, 2017. -





 下载:
下载:


 下载:
下载:
