基于非线性因子的改进鸟群算法在动态能耗管理中的应用

罗钧; 刘泽伟; 张平; 刘学明; 柳政

doi:10.11999/JEIT190264

基于非线性因子的改进鸟群算法在动态能耗管理中的应用

doi: 10.11999/JEIT190264

罗钧^1, ,,
刘泽伟¹,
张平²,
刘学明²,
柳政²

1.
重庆大学光电技术及系统教育部重点实验室重庆 400030
2.
兵器工业 5011 区域计量站重庆 400050

基金项目: 国防科工局十二五(跨十三五)技术基础科研项目(JSJL2014209B004, JSJL2014209B005)

详细信息

作者简介:
罗钧：男，1963年生，教授，博士生导师，研究方向为模式识与人工智能、精密机械及测试计量、智能信息处理

刘泽伟：男，1994年生，硕士生，研究方向为嵌入式系统、精密仪器及机械、测试计量技术及仪器

张平：男，1970年生，硕士生，研究方向为精密仪器及机械、测试计量技术及仪器

刘学明：男，1963年生，硕士生，研究方向为精密仪器及机械、测试计量技术及仪器

通讯作者:
罗钧　luojun@cqu.edu.cn

中图分类号: TP316.7
计量
- 文章访问数: 2883
- HTML全文浏览量: 798
- PDF下载量: 56
- 被引次数: 0
出版历程
- 收稿日期: 2019-04-18
- 修回日期: 2019-10-08
- 网络出版日期: 2019-10-16
- 刊出日期: 2020-03-19

Application of Improved Bird Swarm Algorithm Based on Nonlinear Factor in Dynamic Energy Management

1.
Key Laboratory of Optoelectronic Technology and System of Ministry of Education, Chongqing University, Chongqing 400030, China
2.
5011 District Measurement Station of Weapon Industry, Chongqing 400050, China

Funds: The Science, Technology and Industry Bureau for National Defense 12th Five-year (13th Five-year) Basic Technology Research Projects (JSJL2014209B004, JSJL2014209B005)

摘要

摘要:
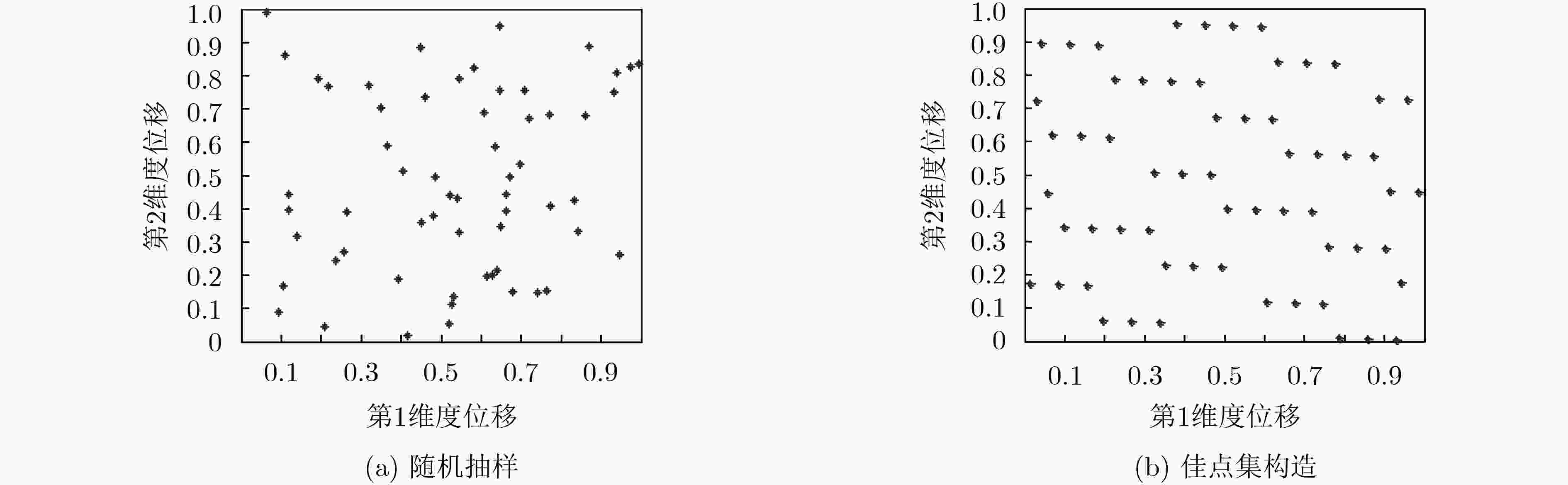
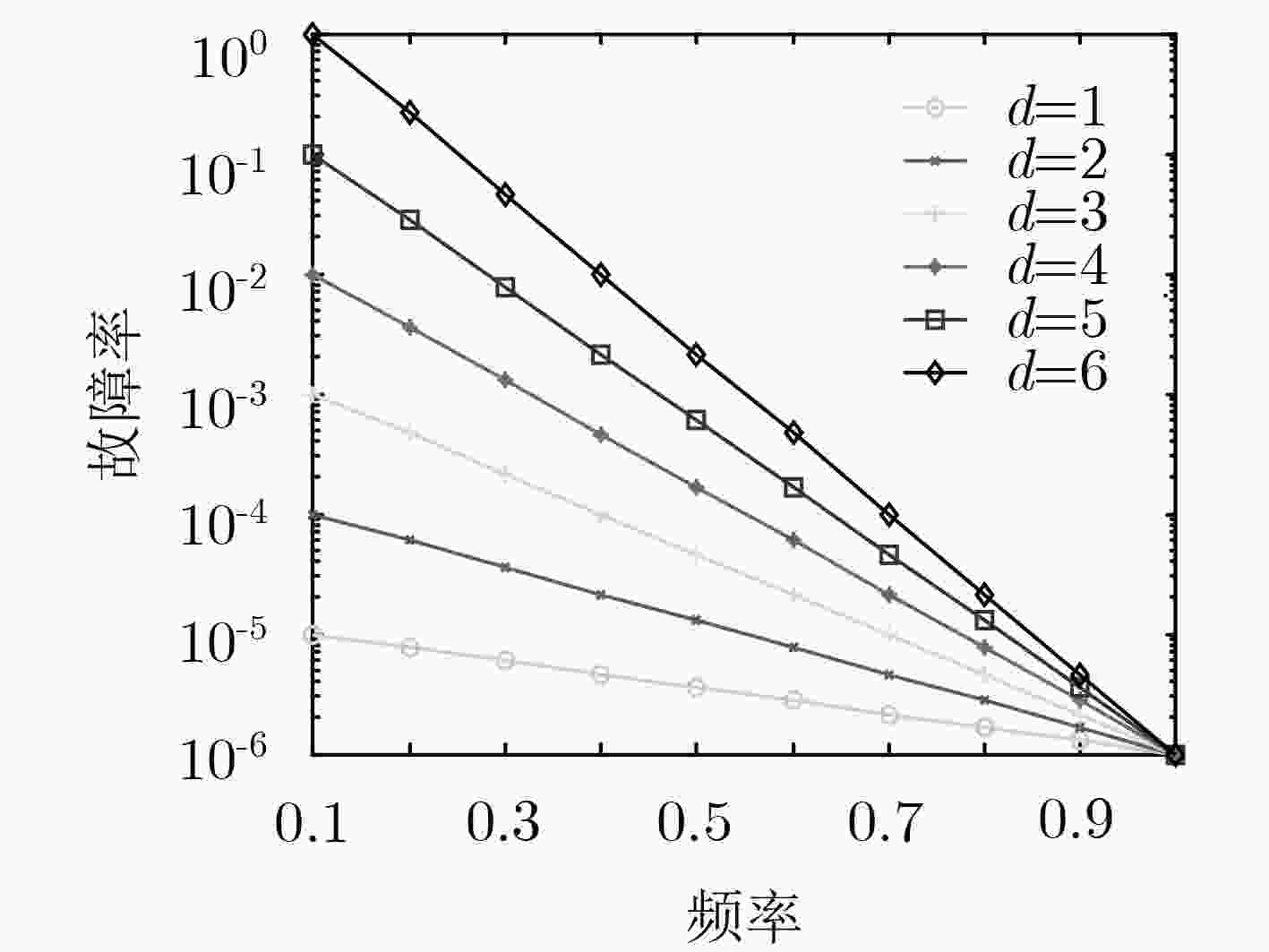
针对实时系统能耗管理中动态电压调节(DVS)技术的应用会导致系统可靠性下降的问题，该文提出一种基于改进鸟群(IoBSA)算法的动态能耗管理法。首先，采用佳点集原理均匀地初始化种群，从而提高初始解的质量，有效增强种群多样性；其次，为了更好地平衡BSA算法的全局和局部搜索能力，提出非线性动态调整因子；接着，针对嵌入式实时系统中处理器频率可以动态调整的特点，建立具有时间和可靠性约束的功耗模型；最后，在保证实时性和稳定性的前提下，利用提出的IoBSA算法，寻求最小能耗的解决方案。通过实验结果表明，与传统BSA等常见算法相比，改进鸟群算法在求解最小能耗上有着很强的优势及较快的处理速度。
- 能耗管理 /
- 实时系统 /
- 动态电压调节 /
- 改进鸟群算法
Abstract:
The application of Dynamic Voltage Scaling (DVS) technique in real-time system energy management will result in the decrease of system reliability. A dynamic energy management method based on Improved Bird Swarm Algorithm (IoBSA) is proposed in this paper. Firstly, the population is initialized uniformly with the principle of good point set, so as to improve the quality of initial solution and increase the diversity of population effectively. Secondly, in order to balance better the global and local search ability of BSA algorithm, the nonlinear dynamic adjustment factor is proposed. Then, a power consumption model with time and reliability constraints is established for the dynamic adjustment of processor frequency in embedded real-time systems. On the premise of ensuring real-time performance and stability, the proposed IoBSA algorithm is used to find the solution with minimum energy consumption. The experimental results show that compared with the traditional BSA algorithm and other common algorithms, the improved bird swarm algorithm has a strong advantage in solving the minimum energy consumption and a fast processing speed energy management.
- Energy management /
- Real-time system /
- Dynamic Voltage Scaling (DVS) /
- Improved Bird Swarm Algorithm (IoBSA)

HTML全文

图 1 两种方法初始化点图

下载: 全尺寸图片幻灯片

图 2 频率故障率

下载: 全尺寸图片幻灯片

图 3 收敛曲线图

下载: 全尺寸图片幻灯片

表 1 部分算法参数列表

算法	参数设置
BSA	$C = S = 1.5,{a_1} = {a_2} = 1,{\rm FQ} = 5,P \in [0.8,\,1]$ ${\rm FL} \in [0.5,\,0.9]$
LSABSA	${a_1} = {a_2} = 1,{\rm FQ} = 5,P \in [0.8,\,1],{\rm FL} \in [0.5,\,0.9]$ ${C_{\rm{e}}} = {S_{\rm{s}}} = 0,5,{C_{\rm{s}}} = {S_{\rm{e}}} = 2.5$
本文	${a_1} = {a_2} = 1,{\rm FQ} = 5,P \in [0.8,1],{\rm FL} \in [0.5,\,0.9]$
IoBSA	${C_{\rm{e}}} = {S_{\rm{s}}} = 0,5,{C_{\rm{s}}} = {S_{\rm{e}}} = 2$
CBSA	${Q_{\min }} = 0,{Q_{\max }} = 2,A = 0.7,r = 0.4,{P_\alpha } = 0.25$
CJADE	$F = 0.8,{C_r} = 0.5,c = 0.1,p = 0.05$
文献[10]	${\rm{limit}} = 50$

下载: 导出CSV

表 2 实验参数列表

参数名	值	参数名	值
种群数	60	任务量	10 30 50
归一化频率	0.1～1.0	截止时间	20～220
WCET	20～50	迭代次数	1000
运行次数	20	惩罚因子	5000

下载: 导出CSV

表 3 任务量为10的优化结果

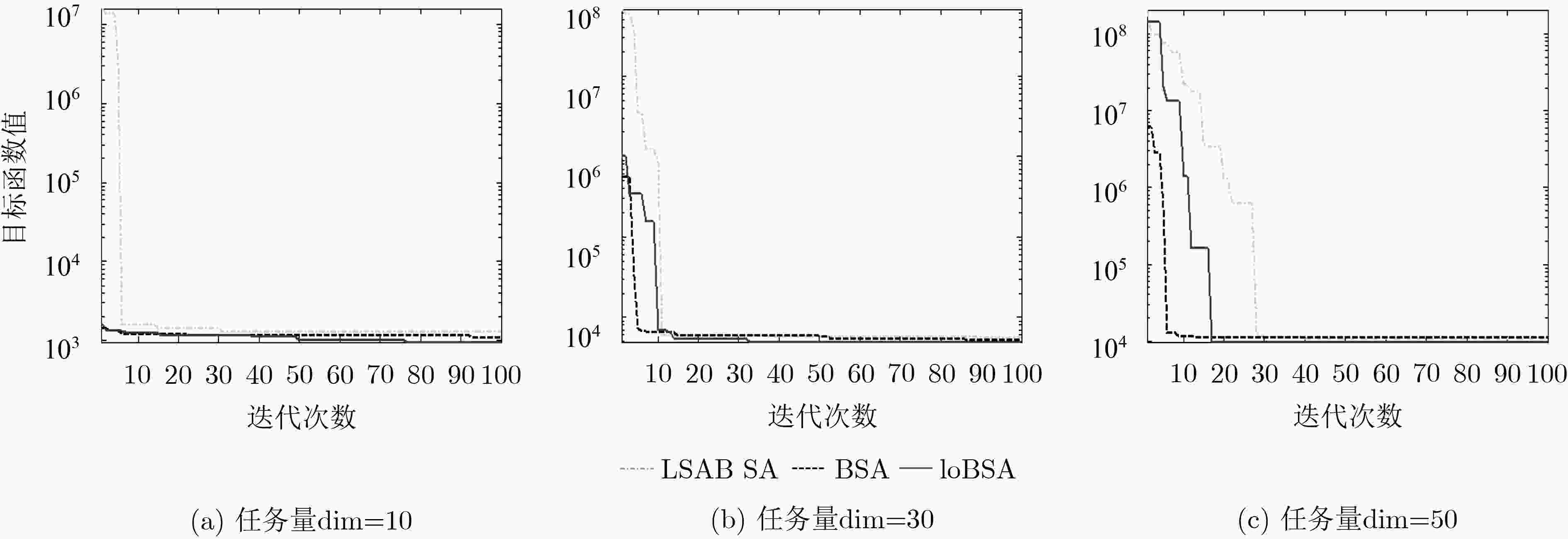
NPM-Val	St.	BSA	本文IoBSA	LSABSA	CSBA	GWO	CJADE	文献[10]
375.57	Best	853.45	821.52	896.57	1040.55	830.83	904.09	1187.05
(min)	Worst	1110.96	1040.01	1090.47	1178.55	1053.47	1123.84	1061.25
3427.05	Mean	967.95	913.04	1005.06	1105.57	964.94	1035.83	1147.21
(max)	Std.Dev	58.18	57.66	60.36	34.85	50.46	53.92	55.25

下载: 导出CSV

表 4 任务量为30的优化结果

NPM-Val	St.	BSA	本文IoBSA	LSABSA	CSBA	GWO	CJADE	文献[10]
1126.70	Best	4355.13	3642.20	4197.41	4048.74	4353.49	4382.29	4881.90
(min)	Worst	5158.38	4936.64	5175.33	5033.73	5234.853	5021.29	5470.92
10281.15	Mean	4771.52	4368.30	4739.58	4519.13	4681.22	4677.56	4928.57
(max)	Std.Dev	215.87	345.31	269.02	238.77	223.95	150.11	304.62

下载: 导出CSV

表 5 任务量为50的优化结果

NPM-Val	St.	BSA	本文IoBSA	LSABSA	CSBA	GWO	CJADE	文献[10]
1877.83	Best	8572.38	8281.54	8610.62	无效	8384.88	8416.94	无效
(min)	Worst	10442.74	10023.18	10149.21	无效	无效	无效	无效
17135.25	Mean	9557.82	9319.57	9513.31	无效	无效	无效	无效
(max)	Std.Dev	587.00	535.50	520.50	643448.64	529852.01	75029.97	1147609.95

下载: 导出CSV

参考文献(20)

SALEHI M E, SAMADI M, NAJIBI M, et al. Dynamic voltage and frequency scheduling for embedded processors considering power/performance tradeoffs[J]. IEEE Transactions on Very Large Scale Integration (VLSI) Systems, 2011, 19(10): 1931–1935. doi: 10.1109/tvlsi.2010.2057520

TERZOPOULOS G and KARATZA H. Performance evaluation and energy consumption of a real-time heterogeneous grid system using DVS and DPM[J]. Simulation Modelling Practice and Theory, 2013, 36: 33–43. doi: 10.1016/j.simpat.2013.04.006

ERNST D, DAS S, LEE S, et al. Razor: Circuit-level correction of timing errors for low-power operation[J]. IEEE Micro, 2004, 24(6): 10–20. doi: 10.1109/MM.2004.85

RONG Peng, PEDRAM M. Energy-aware task scheduling and dynamic voltage scaling in a real-time system[J]. Journal of Low Power Electronics, 2008, 4(1): 1–10. doi: 10.1166/jolpe.2008.154

韩文雅, 王雷. 基于混合任务模型的动态电压调度在无线传感器网络中的应用[J]. 计算机应用, 2010, 30(9): 2522–2525. doi: 10.3724/SP.J.1087.2010.02522

HAN Wenya and WANG Lei. Application of dynamic voltage scaling based on hybrid-task model in wireless sensor network[J]. Journal of Computer Applications, 2010, 30(9): 2522–2525. doi: 10.3724/SP.J.1087.2010.02522

ZHAO Baoxian, AYDIN H, and ZHU Dakai. On maximizing reliability of real-time embedded applications under hard energy constraint[J]. IEEE Transactions on Industrial Informatics, 2010, 6(3): 316–328. doi: 10.1109/tii.2010.2051970

晏福, 徐建中, 李奉书. 混沌灰狼优化算法训练多层感知器[J]. 电子与信息学报, 2019, 41(4): 872–879. doi: 10.11999/JEIT180519

YAN Fu, XU Jianzhong, and LI Fengshu. Training multi-layer perceptrons using chaos grey wolf optimizer[J]. Journal of Electronics &Information Technology, 2019, 41(4): 872–879. doi: 10.11999/JEIT180519

张兴明, 殷从月, 魏帅, 等. 基于双仲裁机制和田口正交法的猫群优化任务调度算法[J]. 电子与信息学报, 2018, 40(10): 2521–2528. doi: 10.11999/JEIT180215

ZHANG Xingming, YIN Congyue, WEI Shuai, et al. Cat swarm optimization task scheduling algorithm based on double arbitration mechanism and Taguchi orthogonal method[J]. Journal of Electronics &Information Technology, 2018, 40(10): 2521–2528. doi: 10.11999/JEIT180215

肖乐意, 欧阳红林, 范朝冬. 基于记忆分子动理论优化算法的多目标截面投影Otsu图像分割[J]. 电子与信息学报, 2018, 40(1): 189–199. doi: 10.11999/JEIT170301

XIAO Leyi, OUYANG Honglin, and FAN Chaodong. Multi-objective cross section projection Otsu's method based on memory knetic-molecular theory optimization algorithm[J]. Journal of Electronics &Information Technology, 2018, 40(1): 189–199. doi: 10.11999/JEIT170301

罗钧, 刘永锋, 付丽. 能耗限制的实时周期任务可靠性感知调度[J]. 重庆大学学报, 2011, 34(8): 86–89. doi: 10.11835/j.issn.1000-582x.2011.08.015

LUO Jun, LIU Yongfeng, and FU Li. Reliability-aware schedule of periodic tasks in energy-constrained real-time systems[J]. Journal of Chongqing University, 2011, 34(8): 86–89. doi: 10.11835/j.issn.1000-582x.2011.08.015

MENG Xianbing, GAO X Z, LU Lihua, et al. A new bio-inspired optimisation algorithm: bird swarm algorithm[J]. Journal of Experimental & Theoretical Artificial Intelligence, 2016, 28(4): 673–687. doi: 10.1080/0952813X.2015.1042530

杨文荣, 马晓燕, 边鑫磊. 基于Levy飞行策略的自适应改进鸟群算法[J]. 河北工业大学学报, 2017, 46(5): 10–16. doi: 10.14081/j.cnki.hgdxb.2017.05.002

YANG Wenrong, MA Xiaoyan, and BIAN Xinlei. Adaptive improved bird swarm algorithm based on Levy flight strategy[J]. Journal of Hebei University of Technology, 2017, 46(5): 10–16. doi: 10.14081/j.cnki.hgdxb.2017.05.002

李延延, 万仁霞. 一种改进算的鸟群算法[J]. 微电子学与计算机, 2018, 35(9): 79–84.

LI Yanyan and WAN Renxia. An improved algorithm for bird swarm optimization[J]. Microelectronics &Computer, 2018, 35(9): 79–84.

吴军, 王龙龙. 基于双鸟群混沌优化的Otsu图像分割算法[J]. 微电子学与计算机, 2018, 35(12): 119–124. doi: 10.19304/j.cnki.issn1000-7180.2018.12.024

WU Jun and WANG Longlong. An Otsu image segmentation algorithm based on chaos optimization of two BSA[J]. Microelectronics &Computer, 2018, 35(12): 119–124. doi: 10.19304/j.cnki.issn1000-7180.2018.12.024

王进成, 高岳林. 基于改进的鸟群算法求解农产品冷链物流配送路径优化问题[J]. 安徽农业科学, 2018, 46(25): 1–4. doi: 10.13989/j.cnki.0517-6611.2018.25.001

WANG Jincheng and GAO Yuelin. Optimization problem of cold chain logistics distribution path of agricultural products based on improved algorithm of bird swarm optimization[J]. Journal of Anhui Agricultural Sciences, 2018, 46(25): 1–4. doi: 10.13989/j.cnki.0517-6611.2018.25.001

谢国民, 干毅军, 丁会巧. 基于佳点集的蝙蝠定位算法在WSN中应用[J]. 传感技术学报, 2017, 30(8): 1252–1257. doi: 10.3969/j.issn.1004-1699.2017.08.021

XIE Guomin, GAN Yijun, and DING Huiqiao. A positioning algorithm based on bat algorithm and good-point setsin the application of WSN[J]. Chinese Journal of Sensors and Actuators, 2017, 30(8): 1252–1257. doi: 10.3969/j.issn.1004-1699.2017.08.021

ZHU D, MELHEM R, and CHILDERS B. Scheduling with dynamic voltage/speed adjustment using slack reclamation in multi-processor real-time systems[C]. Proceedings of the 22nd IEEE Real-time Systems Symposium, London, UK, 2001: 84–94.

SHEHAB M, KHADER A T, LAOUCHEDI M, et al. Hybridizing cuckoo search algorithm with bat algorithm for global numerical optimization[J]. The Journal of Supercomputing, 2019, 75(5): 2395–2422. doi: 10.1007/s11227-018-2625-x

MIRJALILI S, MIRJALILI S M, and LEWIS A. Grey wolf optimizer[J]. Advances in Engineering Software, 2014, 69: 46–61. doi: 10.1016/j.advengsoft.2013.12.007

罗钧, 杨永松, 侍宝玉. 基于改进的自适应差分演化算法的二维Otsu多阈值图像分割[J]. 电子与信息学报, 2019, 41(8): 2017–2024. doi: 10.11999/JEIT180949

LUO Jun, YANG Yongsong, and SHI Baoyu. multi-threshold image segmentation of 2D Otsu based on improved adaptive differential evolution algorithm[J]. Journal of Electronics &Information Technology, 2019, 41(8): 2017–2024. doi: 10.11999/JEIT180949

施引文献

资源附件(0)

访问统计