Design and Implementation of Generic Low-entropy High-order Composite Field Based Masking Scheme
-
摘要:
通过对基于复合域S-box构造算法的深入研究,该文提出一种低面积复杂度的通用低熵高阶掩码算法。在有限域GF(24)上引入低熵掩码思想,并采用部分模块复用设计,有效降低了基于复合域S-box求逆运算的乘法数量。该算法能够适用于由求逆运算构成的任意分组加密算法,进一步将本方案应用于分组加密算法高级加密标准(AES),给出了详细的综合仿真结果并进行了版图面积优化,较传统的掩码方案相比有效减少了逻辑资源的使用,此外,对其安全性进行了理论验证。
Abstract:Based on the in-depth research on the S-box constitution arithmetic of composite, an area optimized generic low-entropy higher-order masking scheme is proposed in this paper. The low entropy masking method is introduced on GF(24), and the partial module reusing design is adopted, which reduces effectively the number of multiplications based on the S-box inversion operation of the composite. The algorithm can be applied to any order masking scheme of arbitrary S-box composed of inversion operation. This scheme is applied to AES, gives detailed simulation results and optimizes the layout area, compared with the traditional masking scheme, reduces effectively the use of logical resources. In addition, the security is theoretically proved.
-
Key words:
- High-order masking /
- Composite arithmetic /
- S-box /
- Low entropy /
- Advanced Encryption Standard(AES)
-
表 1 低熵通用高阶掩码算法
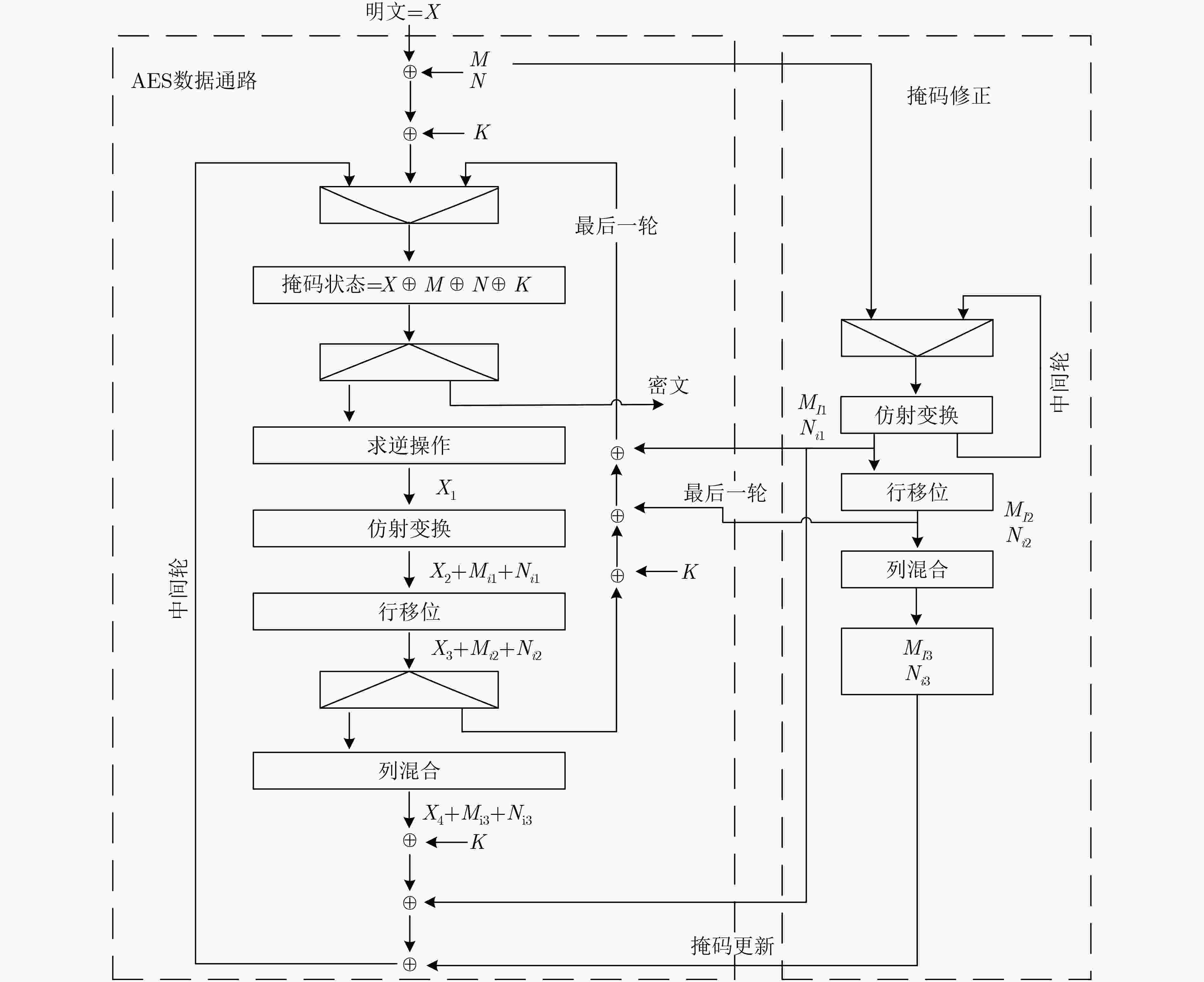
算法1 低熵通用高阶掩码算法 输入:经掩码值$x = a + {m_1} + {m_2} + ··· + {m_d}$,掩码值${m_1},{m_2}, ··· ,{m_d}$ 输出:输入值的求逆${a^{ - 1}} + {m_1} + {m_2} + ··· + {m_d}$ (1) 通过同构矩阵$ \delta $,将有限域${\rm{GF}}({2^k})$上的输入值$x,$m1, m2, ··· ,md分别映射到有限域${\rm{GF}}({2^n})$上,$({x_h},{x_l}){\rm{ }} \leftarrow x$; $({m_{h1}},{m_{l1}}) \leftarrow {m_1}$;
$({m_{h2}},{m_{l2}}) \leftarrow {m_2}$; ··· ; $({m_{hd}},{m_{ld}}) \leftarrow {m_d}$;(2) 将有限域${\rm{GF}}({2^k})$上的求逆运算转化成有限域${\rm{GF}}({2^n})$上的加法、乘法,求逆运算; (3) 利用有限域${\rm{GF}}({2^n})$上的运算求取$d$的掩码防护值$d + {m_{h1} } + {m_{h2} } + ··· + {m_{hd} }$,$\begin{align} d + {m_{h1}} + {m_{h2}} + ··· + {m_{hd}} = & {f_d}({x_h},({x_l} + {m_{h1}} + {m_{h2}} + ··· + {m_{hd}} + {m_{l1}} + {m_{l2}} + ··· + {m_{ld}}),\\&({x_h} + {x_l} + {m_{l1}} + {m_{l2}} + ··· + {m_{ld}}),{m_{h1}},{m_{h2}}, ··· ,{m_{hd}},{m_{l1}},{m_{l2}}, ··· ,{m_{ld}},{{\rm{P}}_0})\\ =& {a_h}^2 \times {{\rm{P}}_0} + {a_h} \times {a_l} + {a_l}^2 + {m_{h1}} + {m_{h2}} + ··· + {m_{hd}};\end{align}$ (4) 在有限域${\rm{GF}}({2^n})$上对$d + {m_{h1}} + {m_{h2}} + ··· + {m_{hd}}$进行掩码求逆,求逆结果为${d^{ - 1}} + {m_{h1}} + {m_{h2}} + ··· + {m_{hd}}$; (5) 利用有限域${\rm{GF}}({2^n})$上的运算求取${x_h},{x_l}$的掩码防护值${x_h}^\prime + {m_{h1}} + {m_{h2}} + ··· + {m_{hd}}$, ${x_l}^\prime + {m_{l1} } + {m_{l2} } + ··· + {m_{ld} }$, $\begin{align}\quad\quad\ \; {x_h}^\prime + {m_{h1}} + {m_{h2}} + ··· + {m_{hd}} =& {f_{bh}}({x_h},({d^{ - 1}} + {m_{h1}} + {m_{h2}} + ··· + {m_{hd}}),\\&({x_h} + {m_{h1}} + {m_{h2}} + ··· + {m_{hd}} + {d^{ - 1}} + {m_{h1}} + {m_{h2}} + ··· + {m_{hd}}){\rm{ }},{m_{h1}},{m_{h2}}, ··· ,{m_{hd}})\\ = & {a_h} \times {d^{ - 1}} + {m_{h1}} + {m_{h2}} + ··· + {m_{hd}};\end{align}$$\begin{align}\quad\quad\ \; {x_l}^\prime + {m_{l1}} + {m_{l2}} + ··· + {m_{ld}} =& {f_{bl}}({x_h},({d^{ - 1}} + {m_{h1}} + {m_{h{\rm{2}}}} + ··· + {m_{hd}}), ({x_l} + {m_{h1}} + {m_{h{\rm{2}}}} + ··· + {m_{hd}} + {m_{l1}} + {m_{l2}} + ··· + {m_{ld}}),\\&({x_h} + {x_l} + {m_{l1}} + {m_{l2}} + ··· + {m_{ld}}) ,{m_{h1}},{m_{h2}}, ··· ,{m_{hd}},{m_{l1}},{m_{l2}}, ··· ,{m_{ld}})\\ =& ({a_h} + {a_l}) \times {d^{ - 1}} + {m_{l1}} + {m_{l2}} + ··· + {m_{ld}};\end{align}$ (6) 通过同构逆矩阵${{ \delta} ^{ - 1} }$,将有限域${\rm{GF}}({2^n})$上的求逆结果映射回有限域${\rm{GF}}({2^k})$上,得到有限域${\rm{GF}}({2^k})$上求逆结果
${a^{ - 1}} + {m_1} + {m_2} + {\rm{ }} ··· + {m_d}$。表 2 AES低熵通用高阶掩码算法
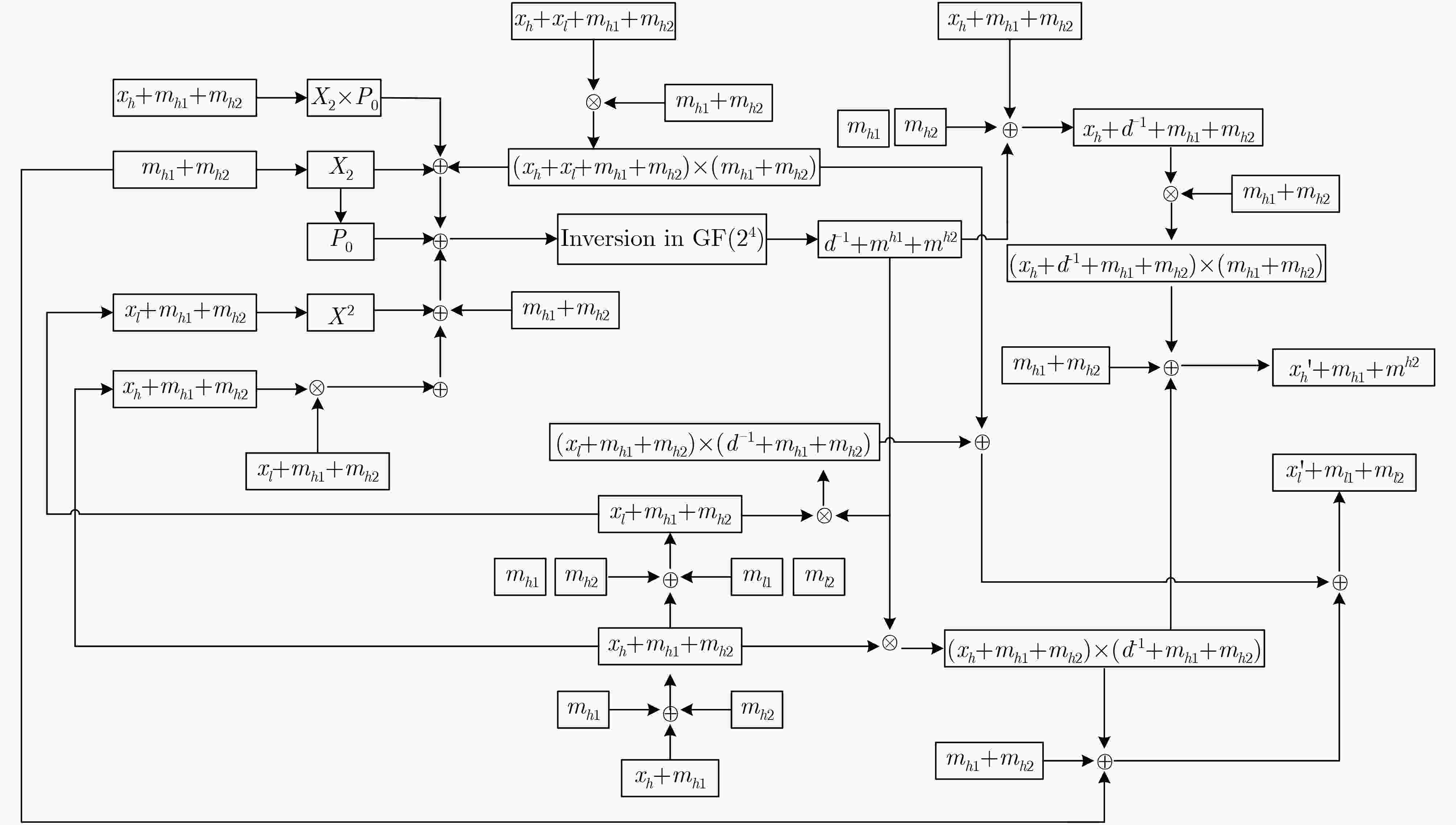
算法2 有限域${\rm{GF}}({2^k})$上对掩码单元$a' = a + {m_1} + {m_2}$求逆 输入:$(x = a + {m_1} + {m_2},{m_1},{m_2}) \in {\rm{GF}}({2^k})$ 输出:$(x' = {a^{ - 1}} + {m_1} + {m_2})$ (1) 映射${ \delta} ({m_1}) \to ({m_{h1} },{m_{l1} }) \in {\rm{GF} }({2^n})$,
映射$\delta ({m_2}) \to ({m_{h2}},{m_{l2}}) \in {\rm{GF}}({2^n})$;(2) 映射$\delta (x) \to ({x_h},{x_l}) \in {\rm{GF}}({2^n})$,即$\{ ({x_h},{x_l}) = ({a_h} + {m_{h1}} + {m_{h2}},{a_h} + {m_{l1}} + {m_{l2}})\} $;
$\begin{align}(3) \ d + {m_{h1}} + {m_{h2}} =& {({x_h})^2}{{\rm{P}}_0} + {m_h}{_1^2}{{\rm{P}}_0} + {m_h}{_2^2}{{\rm{P}}_0} + {({x_l} + {m_{h1}} + {m_{h2}} + {m_{l1}} + {m_{l2}})^2} + {x_h}({x_l} + {m_{h1}} + {m_{h2}} + {m_{l1}} + {m_{l2}})\\ &+ ({x_h} + {x_l} + {m_{l1}} + {m_{l2}})({m_{h1}} + {m_{h2}}) + {m_h}{_1^2} + {m_h}{_2^2} + {m_{h1}} + {m_{h2}};\end{align}$(4) ${d^{ - 1} } + {m_{h1} } + {m_{h2} } =\text{算法}2.(d + {m_{h1} } + {m_{h2} },{m_{h1} },{m_{h2} })$; (5) ${x_h}^\prime + {m_{h1}} + {m_{h2}} = {x_h}({d^{ - 1}} + {m_{h1}} + {m_{h2}}) + ({x_h} + {d^{ - 1}} + {m_{h1}} + {m_{h2}} + {m_{h1}} + {m_{h2}})({m_{h1}} + {m_{h2}}) + {m_{h1}} + {m_{h2}}$;
$\begin{align}(6) \ {x_l}^\prime + {m_{l1}} + {m_{l2}} =& {x_h}({d^{ - 1}} + {m_{h1}} + {m_{h2}}) + ({x_l} + {m_{h1}} + {m_{h2}} + {m_{l1}} + {m_{l2}})({d^{ - 1}} + {m_{h1}} + {m_{h2}}) + ({x_h} + {x_l} + {m_{l1}} + {m_{l2}})({m_{h1}} \\&+ {m_{h2}}) + {m_h}{_1^2} + {m_h}{_2^2} + {m_{l1}} + {m_{l2}}{text{;}}\end{align}$(7) 映射${\delta ^{ - 1}}({x_h}^\prime + {m_{h1}} + {m_{h2}},{x_l}^\prime + {m_{l1}} + {m_{l2}}) \to {\rm{ }}({a^{ - 1}} + {m_1} + {m_2})$。 表 4 不同S-box方案实现结果对比情况
表 5 不同AES方案实现结果对比方案
思想 总的逻辑单元 组合逻辑 总的寄存器 非掩码 23890(21%) 19811(17%) 10769(9%) Oswald[12]
1阶掩码45549(40%)
(90.7%)40368(35%)
(103.8%)16036(14%)
(48.9%)汪鹏君[17]
1阶掩码42161(37%)
(76.5%)36584(32%)
(84.7%)13780(12%)
(28%)Ahn[18]
1阶掩码42087(37%)
(76.2%)36510(32%)
(84.3%)12820(11%)
(19%)本文方法
1阶掩码38456(34%)
(60.9%)32879(28%)
(66.1%)12820(11%)
(19%%)本文方法
2阶掩码44475(39%)
(86.1%)38282(33%)
(93.2%)18980(17%)
(76.2%%)表 6 本方案S-box不同掩码阶数的综合结果
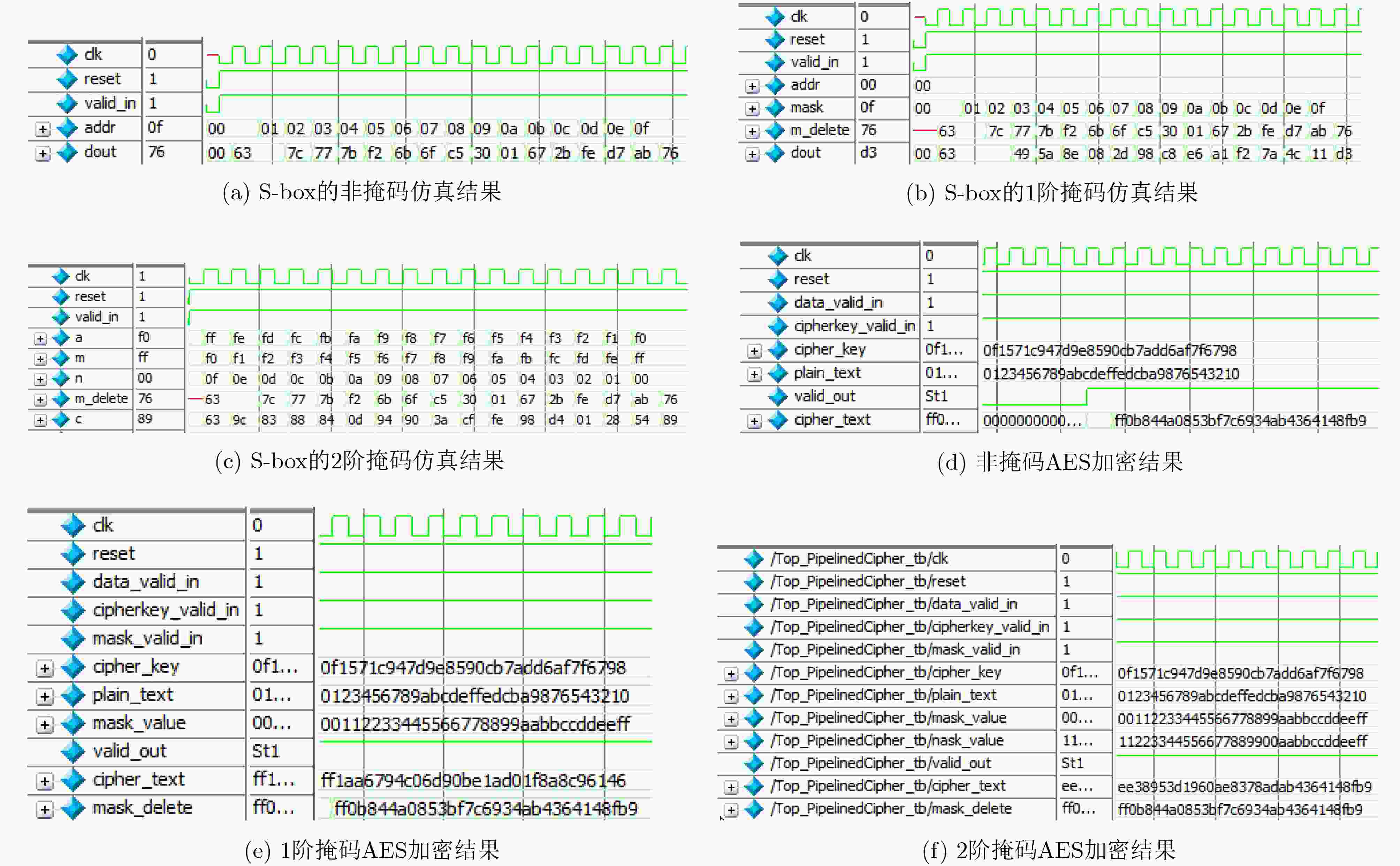
掩码阶数 逻辑名称 逻辑面积(μm2) 合计(μm2) 非掩码S-box 组合逻辑,缓冲器/反相器逻辑,非组合逻辑 221, 14, 46 268 1阶掩码S-box 组合逻辑,缓冲器/反相器逻辑,非组合逻辑 489, 19, 88 577 2阶掩码S-box 组合逻辑,缓冲器/反相器逻辑,非组合逻辑 551, 22, 88 639 表 7 本方案AES不同掩码阶数的综合结果
掩码阶数 逻辑名称 逻辑面积(μm2) 合计(μm2) 非掩码AES 组合逻辑,缓冲器/反相器逻辑,非组合逻辑 14484, 586, 53834 67518 1阶掩码AES 组合逻辑,缓冲器/反相器逻辑,非组合逻辑 53626, 2888, 59614 113241 2阶掩码AES 组合逻辑,缓冲器/反相器逻辑,非组合逻辑 116797, 4594, 100564 217361 -
HUANG Hai, LIU Leibo, HUANG Qihuan, et al. Low area-overhead low-entropy masking scheme (LEMS) against correlation power analysis attack[J]. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 2019, 38(2): 208–219. doi: 10.1109/TCAD.2018.2802867 欧庆于, 罗芳, 叶伟伟, 等. 分组密码算法抗故障攻击能力度量方法研究[J]. 电子与信息学报, 2017, 39(5): 1266–1270. doi: 10.11999/JEIT160548OU Qingyu, LUO Fang, YE Weiwei, et al. Metric for defences against fault attacks of block ciphers[J]. Journal of Electronics &Information Technology, 2017, 39(5): 1266–1270. doi: 10.11999/JEIT160548 CORON J S, GREUET A, PROUFF E, et al. Faster evaluation of sboxes via common shares[C]. The 18th International Conference on Cryptographic Hardware and Embedded Systems, Santa Barbara, USA, 2016: 498–514. doi: 10.1007/978-3-662-53140-2_24. 臧鸿雁, 黄慧芳. 基于均匀化混沌系统生成S盒的算法研究[J]. 电子与信息学报, 2017, 39(3): 575–581. doi: 10.11999/JEIT160535ZANG Hongyan and HUANG Huifang. Research on algorithm of generating s-box based on uniform chaotic system[J]. Journal of Electronics &Information Technology, 2017, 39(3): 575–581. doi: 10.11999/JEIT160535 汪鹏君, 张跃军, 张学龙. 防御差分功耗分析攻击技术研究[J]. 电子与信息学报, 2012, 34(11): 2774–2784. doi: 10.3724/SP.J.1146.2012.00555WANG Pengjun, ZHANG Yuejun, and ZHANG Xuelong. Research of differential power analysis countermeasures[J]. Journal of Electronics &Information Technology, 2012, 34(11): 2774–2784. doi: 10.3724/SP.J.1146.2012.00555 王建新, 方华威, 段晓毅, 等. 基于滑动平均的能量分析攻击研究与实现[J]. 电子与信息学报, 2017, 39(5): 1256–1260. doi: 10.11999/JEIT160637WANG Jianxin, FANG Huawei, DUAN Xiaoyi, et al. Research and implementation of power analysis based on moving average[J]. Journal of Electronics &Information Technology, 2017, 39(5): 1256–1260. doi: 10.11999/JEIT160637 CORON J S. Higher order masking of look-up tables[C]. The 33rd Annual International Conference on the Theory and Applications of Cryptographic Techniques Advances in Cryptology, Berlin, Germany, 2014: 441–458. 徐佩. 智能卡AES加密模块抗侧信道攻击掩码技术研究与实现[D]. [硕士论文], 重庆大学, 2015: 26–53.XU Pei. Research and implementation with mask technology on AES encryption module of smartcard against side channel attack[D]. [Master dissertation], The Chongqing University, 2015: 26–53. CARLET C and PROUFF E. Polynomial evaluation and side channel analysis[M]. RYAN P Y A, NACCACHE D, and QUISQUATER J J. The New Codebreakers: Essays Dedicated to David Kahn on the Occasion of His 85th Birthday. Berlin, Heidelberg: Springer, 2016: 315–341. doi: 10.1007/978-3-662-49301-4_20. 黄海, 冯新新, 刘红雨, 等. 基于随机加法链的高级加密标准抗侧信道攻击对策[J]. 电子与信息学报, 2019, 41(2): 348–354. doi: 10.11999/JEIT171211HUANG Hai, FENG Xinxin, LIU Hongyu, et al. Random addition-chain based countermeasure against side-channel attack for advanced encryption standard[J]. Journal of Electronics &Information Technology, 2019, 41(2): 348–354. doi: 10.11999/JEIT171211 NASSAR M, SOUISSI Y, GUILLEY S, et al. RSM: A small and fast countermeasure for AES, secure against 1st and 2nd-order zero-offset SCAs[C]. 2012 Design, Automation & Test in Europe Conference & Exhibition, Dresden, Germany, 2012: 1173–1178. OSWALD E, MANGARD S, PRAMSTALLER N, et al. A side-channel analysis resistant description of the AES s-box[C]. The 12th International Workshop on Fast Software Encryption, Paris, France, 2005: 413–423. doi: 10.1007/11502760_28. ZAKERI B, SALMASIZADEH M, MORADI A, et al. Compact and secure design of masked AES s-box[C]. The 9th International Conference on Information and Communications Security, Zhengzhou, China, 2007: 216–229. TRICHINA E and KORKISHKO T. Secure AES hardware module for resource constrained devices[C]. Proceedings of the 1st European Workshop on Security in Ad-hoc and Sensor Networks, Heidelberg, Germany, 2005: 215–229. doi: 10.1007/978-3-540-30496-8_18. OSWALD E and SCHRAMM K. An efficient masking scheme for AES software implementations[C]. The 6th International Workshop on Information Security Applications. Jeju Island, Korea, 2006: 292–305. KIM H S, HONG S, and LIM J. A fast and provably secure higher-order masking of AES s-box[C]. Proceedings of the 13th International Conference on Cryptographic Hardware and Embedded Systems. Nara, Japan, 2011: 95–107. 汪鹏君, 郝李鹏, 张跃军. 防御零值功耗攻击的AES SubByte模块设计及其VLSI实现[J]. 电子学报, 2012, 40(11): 2183–2187. doi: 10.3969/j.issn.0372-2112.2012.11.007WANG Pengjun, HAO Lipeng, and ZHANG Yuejun. Design of AES subbyte module of anti-zero value power attack and its VLSI implementation[J]. Acta Electronica Sinica, 2012, 40(11): 2183–2187. doi: 10.3969/j.issn.0372-2112.2012.11.007 AHN S and CHOI D. An improved masking scheme for s-box software implementations[C]. The 16th International Workshop on Information Security Applications, Jeju Island, Korea, 2016: 200–212. -





 下载:
下载:



 下载:
下载:
