Image Compressed Sensing Reconstruction Based on Structural Group Total Variation
-
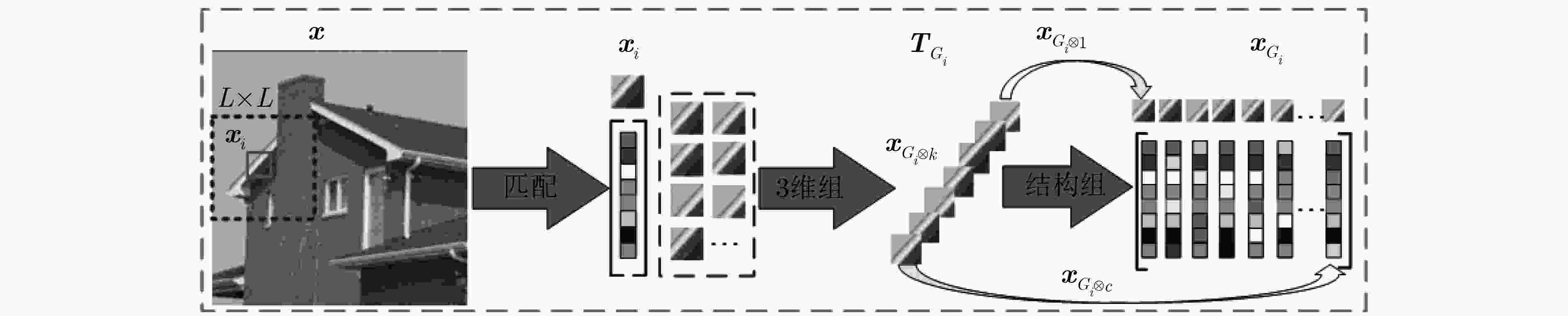
摘要: 针对基于传统全变分(TV)模型的图像压缩感知(CS)重建算法不能有效地恢复图像的细节和纹理,从而导致图像过平滑的问题,该文提出一种基于结构组全变分(SGTV)模型的图像压缩感知重建算法。该算法利用图像的非局部自相似性和结构稀疏特性,将图像的重建问题转化为由非局部自相似图像块构建的结构组全变分最小化问题。算法以结构组全变分模型为正则化约束项构建优化模型,利用分裂Bregman迭代将算法分离成多个子问题,并对每个子问题高效地求解。所提算法很好地利用了图像自身的信息和结构稀疏特性,保护了图像细节和纹理。实验结果表明,该文所提出的算法优于现有基于全变分模型的压缩感知重建算法,在PSNR和视觉效果方面取得了显著提升。Abstract: To solve the problem that the traditional Compressed Sensing (CS) algorithm based on Total Variation (TV) model can not effectively restore details and texture of image, which leads to over-smoothing of reconstructed image, an image Compressed Sensing (CS) reconstruction algorithm based on Structural Group TV (SGTV) model is proposed. The proposed algorithm utilizes the non-local self-similarity and structural sparsity of image, and converts the CS recovery problem into the total variation minimization problem of the structural group constructed by non-local self-similar image blocks. In addition, the optimization model of the proposed algorithm is built with regularization constraint of the structural group total variation model, and it uses the split Bregman iterative algorithm to separate it into multiple sub-problems, and then solves them respectively. The proposed algorithm makes full use of the information and structural sparsity of image to protects the image details and texture. The experimental results demonstrate that the proposed algorithm achieves significant performance improvements over the state-of-the-art total variation based algorithm in both PSNR and visual perception.
-
表 1 基于SGTV模型的图像CS重建算法(SGTV)的整体描述
输入:随机投影测量矩阵${{H}}$和CS测量值${{y}}$ 初始化:$t = 0$, ${{{u}}^{(0)}} = 0$, ${{{b}}^{(0)}} = 0$, $B$, $c$, $\beta $, $\mu $; (1) 开始迭代:$t = 1,2, ··· ,N$ (2) 根据式(10)计算得到${{{u}}^{(t + 1)}}$; (3) 令${{{r}}^{(t + 1)}} = {{{u}}^{(t + 1)}} - {{{b}}^{(t)}}$; ${{\mu = \left( {\lambda K} \right)}/{\left( {\beta N} \right)}}$; (4) 根据块匹配法找到$n$个结构组; (5) 对于每一个结构组${{{r}}_{{G_i}}}$, $i = 1,2, ··· ,n$ (6) 利用FISTA算法迭代更新得到${{{p}}^{m + 1}}$; (7) 根据式(3)算法迭代更新得到${{{\hat x}}_{{G_i}}}$; (8) end for (9) 根据式(11)计算得到${{{x}}^{(t + 1)}}$; (10) 根据式(12)更新${{{b}}^{(t + 1)}}$; (11) 达到最大迭代次数,算法结束 (12) 输出重建图像${{u}} = {{{u}}^{(t + 1)}}$ 表 2 不同采样率下各图像CS重建算法重建图像的PSNR(dB)/FISM值比较
采样率 算法 House Barbara Leaves Monarch Parrots Vessels Avg. 0.2 TV 31.54/0.9072 23.79/0.8190 22.66/0.8553 26.77/0.8862 26.51/0.9018 22.09/0.8356 25.56/0.8675 NLTV 32.59/0.9199 25.01/0.8584 24.40/0.9012 27.07/0.8913 26.52/0.9247 23.54/0.8798 26.51/0.8959 TVNLR 33.03/0.9230 25.68/0.8901 23.51/0.8834 27.42/0.9073 26.97/0.9225 23.34/0.8718 26.66/0.8997 NGSR 33.60/0.9350 27.470.9175 24.79/0.9036 27.83/0.9090 27.43/0.9217 24.10/0.8874 27.54/0.9124 SGTV 34.96/0.9519 29.27/0.9240 26.71/0.9249 28.59/0.9232 29.19/0.9386 25.16/0.9024 28.98/0.9275 0.3 TV 33.76/0.9382 25.16/0.8723 25.79/0.9090 29.94/0.9286 28.68/0.9309 25.27/0.8992 28.10/0.9130 NLTV 34.96/0.9422 27.47/0.9157 27.57/0.9354 29.86/0.9278 29.02/0.9469 27.15/0.9352 29.31/0.9339 TVNLR 35.23/0.9497 27.92/0.9153 26.67/0.9249 30.01/0.9374 28.96/0.9436 27.08/0.9321 29.31/0.9338 NGSR 36.36/0.9679 29.54/0.9435 27.71/0.9359 30.92/0.9419 30.22/0.9526 27.26/0.9358 30.34/0.9463 SGTV 37.08/0.9690 32.20/0.9558 29.91/0.9543 31.55/0.9508 31.17/0.9549 28.36/0.9446 31.73/0.9549 0.4 TV 35.41/0.9564 26.59/0.9095 28.76/0.9419 32.69/0.9520 30.46/0.9513 27.95/0.9441 30.31/0.9452 NLTV 36.97/0.9603 30.01/0.9520 31.04/0.9682 32.66/0.9532 30.15/0.9619 29.70/0.9568 31.76/0.9587 TVNLR 37.19/0.9664 30.27/0.9246 30.14/0.9546 32.95/0.9600 30.40/0.9576 29.35/0.9570 31.72/0.9534 NGSR 37.25/0.9695 31.10/0.9602 31.08/0.9637 33.28/0.9590 31.37/0.9619 30.01/0.9609 32.35/0.9625 SGTV 38.80/0.9775 34.33/0.9710 32.54/0.9702 34.20/0.9664 33.16/0.9666 31.25/0.9668 34.05/0.9698 表 3 采样率为0.3时,各算法的实际运行处理时间(s)
TV NLTV TVNLR NGSR SGTV House (256×256) 5.27 75.26 99.57 110.52 132.85 Vessels(96×96) 1.29 36.75 49.09 63.12 73.96 平均 3.28 56.01 74.33 86.82 103.01 -
DONOHO D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289–1306. doi: 10.1109/TIT.2006.871582 TSAIG Y and DONOHO D L. Extensions of compressed sensing[J]. Signal Processing, 2006, 86(3): 549–571. doi: 10.1016/j.sigpro.2005.05.029 AHARON M, ELAD M, and BRUCKSTEIN A. K-SVD: An algorithm for designing overcomplete dictionaries for sparse representation[J]. IEEE Transactions on Signal Processing, 2006, 54(11): 4311–4322. doi: 10.1109/TSP.2006.881199 SHEN Yangmei, XIONG Hongkai, and DAI Wenrui. Multiscale dictionary learning for hierarchical sparse representation[C]. 2017 IEEE International Conference on Multimedia and Expo, Hong Kong, China, 2017: 1332–1337. ZHANG Jian, ZHAO Chen, ZHAO Debin, et al. Image compressive sensing recovery using adaptively learned sparsifying basis via L0 minimization[J]. Signal Processing, 2014, 103: 114–126. doi: 10.1016/j.sigpro.2013.09.025 LI Chengbo, YIN Wotao, and ZHANG Yin. TVAL3: TV minimization by augmented lagrangian and alternating direction algorithms[EB/OL]. http://www.caam.rice.edu/~optimization/L1/TVAL3/, 2013. HE Wei, ZHANG Hongyan, and ZHANG Liangpei. Total variation regularized reweighted sparse nonnegative matrix factorization for hyperspectral unmixing[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(7): 3909–3921. doi: 10.1109/tgrs.2017.2683719 WAHID A and LEE H J. Image denoising method based on directional total variation filtering[C]. The 8th International Conference on Information and Communication Technology Convergence, Jeju, South Korea, 2017: 798–802. BUADES A, COLL B, and MOREL J M. A non-local algorithm for image denoising[C]. 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Diego, USA, 2005: 60–65. LIU Hangfan, XIONG Ruiqin, ZHANG Xinfeng, et al. Nonlocal gradient sparsity regularization for image restoration[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2017, 27(9): 1909–1921. doi: 10.1109/TCSVT.2016.2556498 ZHANG Jian, ZHAO Debin, and GAO Wen. Group-based sparse representation for image restoration[J]. IEEE Transactions on Image Processing, 2014, 23(8): 3336–3351. doi: 10.1109/TIP.2014.2323127 CAO Wenfei, CHANG Yi, HAN Guodong, et al. Destriping remote sensing image via low-rank approximation and nonlocal total variation[J]. IEEE Geoscience and Remote Sensing Letters, 2018, 15(6): 848–852. doi: 10.1109/LGRS.2018.2811468 SHEN Yan, LIU Qing, LOU Shuqin, et al. Wavelet-based total variation and nonlocal similarity model for image denoising[J]. IEEE Signal Processing Letters, 2017, 24(6): 877–881. doi: 10.1109/LSP.2017.2688707 TU Bing, HUANG Siyuan, FANG Leyuan, et al. Hyperspectral image classification via weighted joint nearest neighbor and sparse representation[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2018, 11(11): 4063–4075. doi: 10.1109/JSTARS.2018.2869376 XU Jin, QIAO Yuansong, FU Zhizhong, et al. Image block compressive sensing reconstruction via group-based sparse representation and nonlocal total variation[J]. Circuits, Systems, and Signal Processing, 2019, 38(1): 304–328. doi: 10.1007/s00034-018-0859-8 ZHANG Xiaoqun, BURGER M, BRESSON X, et al. Bregmanized nonlocal regularization for deconvolution and sparse reconstruction[J]. SIAM Journal on Imaging Sciences, 2010, 3(3): 253–276. doi: 10.1137/090746379 ZHANG Jian, LIU Shaohui, XIONG Ruiqin, et al. Improved total variation based image compressive sensing recovery by nonlocal regularization[C]. 2013 IEEE International Symposium on Circuits and Systems, Beijing, China, 2013: 2836–2839. GOLDSTEIN T and OSHER S. The split Bregman method for L1-regularized problems[J]. SIAM Journal on Imaging Sciences, 2009, 2(2): 323–343. doi: 10.1137/080725891 ZHANG Lin, ZHANG Lei, MOU Xuanqin, et al. FSIM: A feature similarity index for image quality assessment[J]. IEEE Transactions on Image Processing, 2011, 20(8): 2378–2386. doi: 10.1109/TIP.2011.2109730 BECK A and TEBOULLE M. Fast gradient-based algorithms for constrained total variation image denoising and deblurring problems[J]. IEEE Transactions on Image Processing, 2009, 18(11): 2419–2434. doi: 10.1109/TIP.2009.2028250 -





 下载:
下载:






 下载:
下载:
