Interference Recognition Based on Singular Value Decomposition and Neural Network
-
摘要: 无线通信中的抗干扰技术对通信的稳定性和安全性都具有重要意义,干扰识别作为抗干扰技术的重要环节一直是研究的热点。该文提出一种基于奇异值分解与神经网络的干扰识别方法,该方法只计算信号矩阵的奇异值即完成特征提取,与传统方法相比节省了多个谱特性的计算量。仿真结果表明:基于奇异值分解与神经网络的干扰识别方法与传统方法相比在干信比为0 dB左右的条件下识别准确率有10%~25%的提高。Abstract: The anti-interference technology in wireless communication is great significance to the stability and security of communication. As an important part of anti-interference technology, interference recognition is a research hotspot. An interference recognition method based on singular value decomposition and neural network is proposed. This method only calculates the singular value of the signal matrix as the feature. Compared with the traditional method, it saves the computational complexity of multiple spectral features. The simulation results show that the recognition accuracy based on singular value decomposition and neural network is 10%~25% higher than the traditional method under the condition of jamming-signal ratio at 0 dB.
-
Key words:
- Jamming recognition /
- Neural network /
- Singular value decomposition
-
表 1 对单音干扰、线性扫频干扰、部分频带干扰及噪声调频干扰信号的识别率(%)
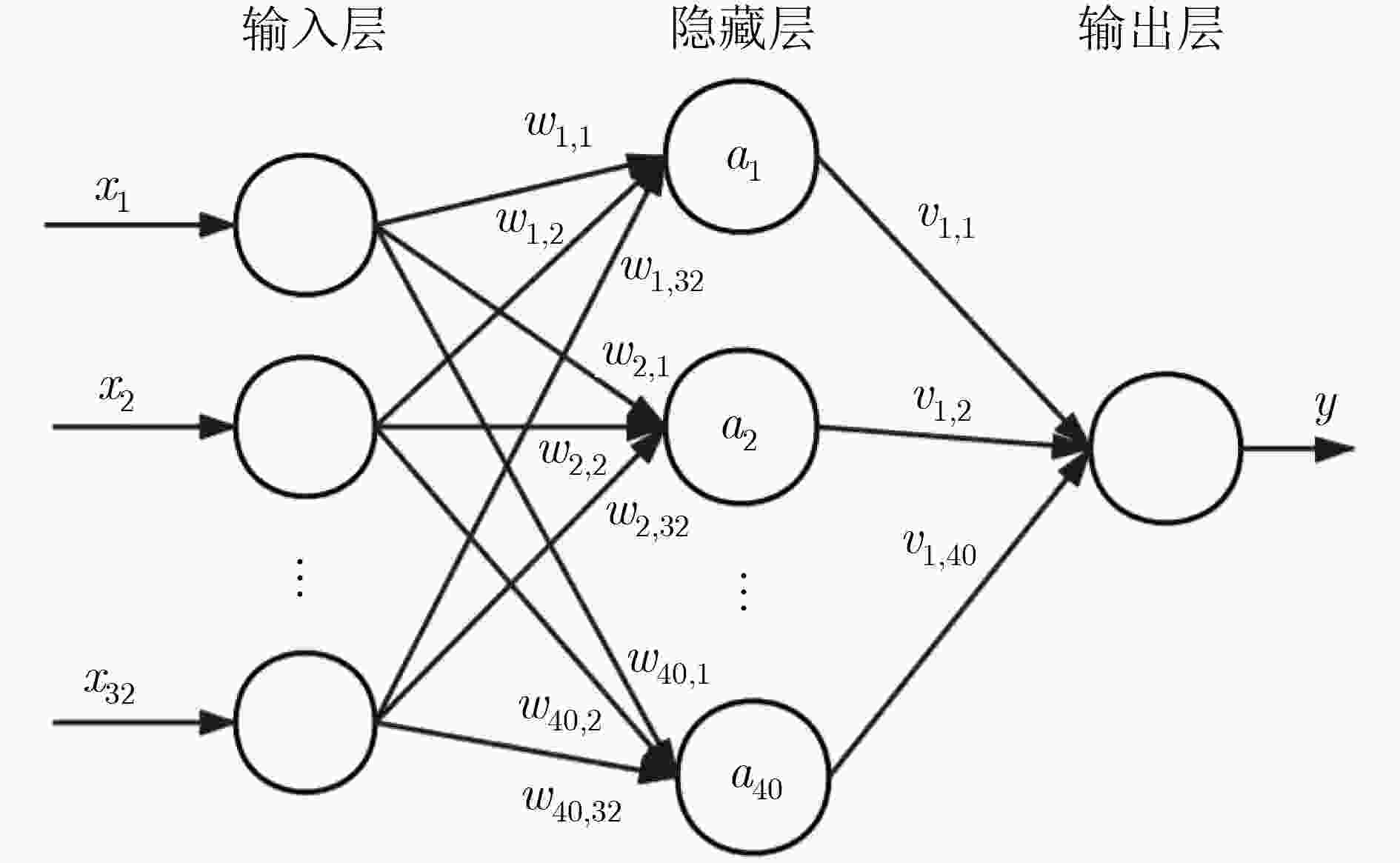
BP神经
网络输入训练样本识别
正确率测试样本识别
正确率奇异值导数 99.753 98.437 -
GRECO M, GINI F, and FARINA A. Radar detection and classification of jamming signals belonging to a cone class[J]. IEEE Transactions on Signal Processing, 2008, 56(5): 1984–1993. doi: 10.1109/TSP.2007.909326 DOBRE O A, ABDI A, BAR-NESS Y, et al. Survey of automatic modulation classification techniques: Classical approaches and new trends[J]. IET Communications, 2007, 1(2): 137–156. doi: 10.1049/iet-com:20050176 AZZOUZ E E and NANDI A K. Automatic identification of digital modulation types[J]. Signal Processing, 1995, 47(1): 55–69. doi: 10.1016/0165-1684(95)00099-2 梁金弟, 程郁凡, 杜越, 等. 联合多维特征的干扰识别技术研究[J]. 信号处理, 2017, 33(12): 1609–1615. doi: 10.16798/j.issn.1003-0530.2017.12.012LIANG Jindi, CHENG Yufan, DU Yue, et al. The research of interference recognition technology based on the joint multi-dimensional features[J]. Journal of Signal Processing, 2017, 33(12): 1609–1615. doi: 10.16798/j.issn.1003-0530.2017.12.012 郝万兵, 马若飞, 洪伟. 基于时频特征提取的雷达有源干扰识别[J]. 火控雷达技术, 2017, 46(4): 11–15. doi: 10.3969/j.issn.1008-8652.2017.04.003HAO Wanbing, MA Ruofei, and HONG Wei. Radar active jamming identification based on time-frequency characteristic extraction[J]. Fire Control Radar Technology, 2017, 46(4): 11–15. doi: 10.3969/j.issn.1008-8652.2017.04.003 程汉文, 朱雷, 吴乐南. 基于累计量的干扰信号调制识别算法[J]. 电子与信息学报, 2009, 31(7): 1741–1745. doi: 10.3724/SP.J.1146.2008.00910CHENG Hanwen, ZHU Lei, and WU Lenan. Modulation classification algorithm for jamming signal based on cumulant[J]. Journal of Electronics &Information Technology, 2009, 31(7): 1741–1745. doi: 10.3724/SP.J.1146.2008.00910 李伟, 魏光辉, 潘晓东, 等. 复杂电磁环境下通信装备干扰预测方法[J]. 电子与信息学报, 2017, 39(11): 2782–2789. doi: 10.11999/JEIT170107LI Wei, WEI Guanghui, PAN Xiaodong, et al. Interference prediction method of communication equipment under complex electromagnetic environment[J]. Journal of Electronics &Information Technology, 2017, 39(11): 2782–2789. doi: 10.11999/JEIT170107 姜丹丹. 张量奇异值及高阶奇异值分解具有的若干性质[D]. [硕士学位论文], 哈尔滨工业大学, 2017.JIANG Dandan. A number of properties of singular value and higher order singular value decomposition of tensor[D]. [Master dissertation], Harbin Institute of Technology, 2017. KALMAN D. A singularly valuable decomposition: The SVD of a matrix[J]. The College Mathematics Journal, 1996, 27(1): 2–23. doi: 10.1080/07468342.1996.11973744 SEILER M C and SEILER F A. Numerical recipes in C: The art of scientific computing[J]. Risk Analysis, 1989, 9(3): 415–416. doi: 10.1111/j.1539-6924.1989.tb01007.x KONG Lei, XU Zhijun, WANG Jinming, et al. A novel algorithm for jamming recognition in wireless communication[C]. The 2013 6th International Congress on Image and Signal Processing, Hangzhou, China, 2013: 1473–1477. doi: 10.1109/CISP.2013.6743907. 章敏敏, 徐和平, 王晓洁, 等. 谷歌TensorFlow机器学习框架及应用[J]. 微型机与应用, 2017, 36(10): 58–60. doi: 10.19358/j.issn.1674-7720.2017.10.017ZHANG Minmin, XU Heping, WANG Xiaojie, et al. Application of Google TensorFlow machine learning framework[J]. Microcomputer &Its Applications, 2017, 36(10): 58–60. doi: 10.19358/j.issn.1674-7720.2017.10.017 徐国进. 典型通信干扰信号识别技术研究[D]. [硕士论文], 电子科技大学, 2018.XU Guojin. Research on identification of typical communication jamming signals[D]. [Master dissertation], University of Electronic Science and Technology of China, 2018. -






 下载:
下载:


 下载:
下载:
