Iterative Fuzzy C-means Clustering Algorithm & K-Nearest Neighbor and Dictionary Data Based Ensemble TSK Fuzzy Classifiers
-
摘要:
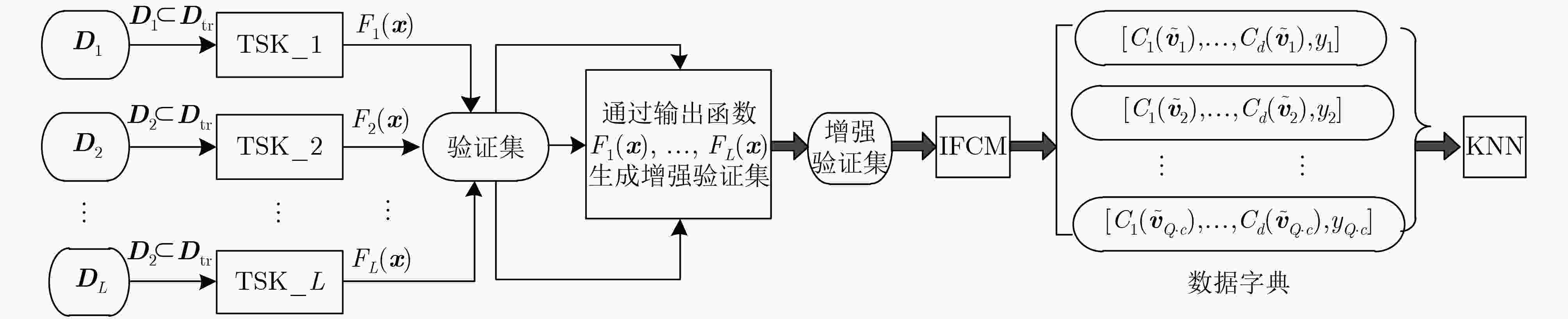
该文提出一种新型的集成TSK模糊分类器(IK-D-TSK),首先通过并行学习的方式组织所有0阶TSK模糊子分类器,然后每个子分类器的输出被扩充到原始(验证)输入空间,最后通过提出的迭代模糊聚类算法(IFCM)作用在增强验证集上生成数据字典,从而利用KNN对测试数据进行快速预测。IK-D-TSK具有以下优点:在IK-D-TSK中,每个0阶TSK子分类器的输出被扩充到原始入空间,以并行方式打开原始(验证)输入空间中存在的流形结构,根据堆栈泛化原理,可以保证提高分类精度;和传统TSK模糊分类器相比,IK-D-TSK以并行方式训练所有的子分类器,因此运行速度可以得到有效保证;由于IK-D-TSK是在以IFCM & KNN所获得的数据字典的基础上进行分类的,因此具有强鲁棒性。理论和实验验证了模糊分类器IK-D-TSK具有较高的分类性能、强鲁棒性和高可解释性。
Abstract:A new ensemble TSK fuzzy classifier (i,e. IK-D-TSK) is proposed. First, all zero-order TSK fuzzy sub-classifiers are organized in a parallel way, then the output of each sub-classifier is augmented to the original (validation) input space, finally, the proposed Iterative Fuzzy C-Means (IFCM) clustering algorithm generates dictionary data on augmented validation dataset, and then KNN is used to predict the result for test data. IK-D-TSK has the following advantages: the output of each zero-order TSK subclassifier is augmented to the original input space to open the manifold structure in parallel, according to the principle of stack generalization, the classification accuracy can be improved; Compared with traditional TSK fuzzy classifiers which trains sequentially, IK-D-TSK trains all the sub-classifiers in parallel, so the running speed can be effectively guaranteed; Because IK-D-TSK works based on dictionary data obtained by IFCM & KNN, it has strong robustness. The theoretical and experimental results show that IK-D-TSK has high classification performance, strong robustness and high interpretability.
-
表 1 IFCM算法
输入:数据集${ { X} } = \{ { { { x} }_1},{ { { x} }_2}, ··· ,{ { { x} }_N}\} \in {R^{N \times D} }$,及其标签$ { { Y} } = $ $\{ {y_1},{y_2}, ··· ,{y_N}\} $,真实类别数Q,每一类的聚类中心点数
c,每一类的样本数${N_1},{N_2}, ··· ,{N_Q}$,最大误差阈值$\tau $。输出:中心点矩阵${{V}}$及其标签。 (1)通过FCM初始化每类中的中心点,然后形成中心点矩阵${{ V}}$。
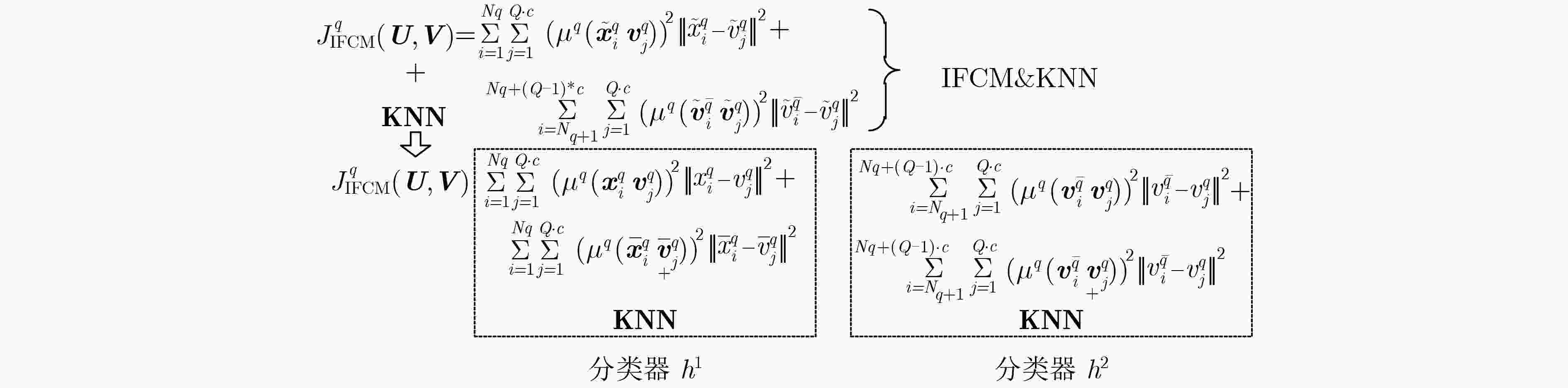
初始化q=1,其中$1 \le q \le Q$。(2)重复; (a)重复; ①当$i \in \left\{ {1,2, ··· ,{N_q}} \right\}$时,通过式(12)和式(13)计算隶属度
${\mu ^q}\left( {{{ x}}_i^q,{{ v}}_j^q} \right)$;当$ i \in \{ {N_q}{\rm{ + }}1,{N_q}{\rm{ + 2}}, ··· ,{N_q}{\rm{ + }}$$\left( {Q - 1} \right) \cdot c \}$
时,通过式(14)和式(15)计算隶属度${\mu ^q}\left( {{{ v}}_i^{\bar q},{{ v}}_j^q} \right)$;②通过式(17)计算中心点${{ v}}_j^q$; (b)直到中心点矩阵保持几乎不变或达到内部迭代的最大次数
为止;(c)利用${{ v}}_j^q$更新中心点矩阵${{ V}}$,并且$q = ( q + $$ 1 ){\rm{ mod }}\;Q$;
(3)直到$\mathop {\max }\limits_{j \in \left\{ {1,2, ··· ,Q \cdot c} \right\}} \left\| {{{ v}}_j^q - {{ v}}_j^{q - 1}} \right\| < \tau $或达到外部最大迭代次
数为止;(4)根据中心点矩阵${{ V}}$输出所有的中心点及其标签。 表 2 IK-D-TSK学习算法
输入:训练数据集${ {{D} }_{\rm tr} }{\rm{ = } }\left[ { { {{X} }_{\rm tr} }\;{ {{Y} }_{\rm tr} } } \right]$,验证数据集${{{D}}_v}{\rm{ = }}\left[ {{{{X}}_v}\;{{{Y}}_v}} \right]$, 其中${ {{X} }_{\rm tr} }$和${{{X}}_v}$分别表示训练数据和验证数据,对应的标
签集为${ {{Y} }_{\rm tr} }$和${{{Y}}_v}$,子分类器数$L$, ${K_1},{K_2}, ··· ,{K_L}$表示每
个子分类器的模糊规则数输出:IK-D-TSK的结构,数据字典 训练过程 (1)初始化:为每个子分类器从${{{D}}_{\rm tr}}$中随机抽样训练数据子集
${{{D}}_1},{{{D}}_2}, \!···\! ,{{{D}}_L}$,并且${{{D}}_1} \cup {{{D}}_2} \cup ······ \cup $${{{D}}_L}={{{D}}_{\rm tr}} $(2)并行训练L个零阶TSK模糊子分类器; (a)为每个子分类器分配模糊规则数; (b)构造5个高斯型隶属度函数,在每一维上从中心点集合{0,
0.25, 0.50, 0.75, 1.00}中随机指定一个值并构造规则组合矩
阵${{{ \varTheta }}_l}{\rm{ = }}{[\upsilon _{ik}^l]_{{K_l} \times d}}$. 通过给每个元素分配一个随机正数来构
造核宽度矩阵${{{ \varPhi }}_l}= {\rm{ [}}\delta _{ik}^l{{\rm{]}}_{{K_l} \times d}}$,利用式(2)计算模糊隶属度,
正则化并构造矩阵$ \qquad{ {{X} }_g} = \left[ {\begin{array}{*{20}{c} }\tilde \omega _1^1 & \tilde \omega _1^2 & ··· & \tilde \omega _1^{ {K_l} }\\\tilde \omega _2^1 & \tilde \omega _2^2 & ···& \tilde \omega _2^{ {K_l} }\\ \vdots & \vdots & \ddots & \vdots \\\tilde \omega _{ {N_l} }^1 & \tilde \omega _{ {N_l} }^2 &··· & \tilde \omega _{ {N_l} }^{ {K_l} }\end{array} } \right]_{ {N_l} \times {K_l} } \qquad\quad (18)$ 通过LLM计算后件参数${{{ a}}_g}$,即 $\qquad\qquad\qquad\ { {{a} }_{\rm g} } = {\left( \left( { {1 / C} } \right){{I} } + { {{X} }_{\rm g}^{\rm T} }{ {{X} }_{\rm g}}\right)^{ - 1} } {{X} }_{\rm g}^{\rm T} {{y} } \qquad\qquad\qquad\ \ (19)$ 其中${{ I}}$是$K \times K$单位矩阵,C是给定的正则化参数; (c)通过式(3)生成L个子分类器的输出函数${F_1}\left( {{ x}} \right),{F_2}\left( {{ x}} \right), $ $ ··· ,{F_L}\left( {{ x}} \right)$; (3)生成增强验证数据集; 对于验证数据集的每个样本,计算对应每个输出函数${F_1}\left( {{ x}} \right)$, $ {F_2}\left( {{ x}} \right), ··· ,{F_L}\left( {{ x}} \right)$的值并将其作为增强特征,将原始特征和增强 特征合并,从而形成增强验证数据集${{ D}}_v^{\rm new}{\rm{ = }}\left[ {{{{ X}}_v}\;{{{\bar { X}}}_v}\;{{{ Y}}_v}} \right]$,其中 ${{\bar { X}}_v}$表示验证数据的增强特征集; (4)生成数据字典; 在${ { D} }_v^{\rm new}$上调用IFCM算法后,生成代表性的中心点及其对应的
标签,去掉增强特征,即得到数据字典。预测过程 (1)对于任何测试样本,利用KNN方法在数据字典上找到最近的
k个点,基于投票策略,确定其类标;(2)输出测试样本的标签。 表 3 数据集
数据集 类别数 特征数 样本数 SATimage(SAT) 6 36 6435 MUShroom(MUS) 2 22 8124 WAVeform3(WAV) 3 21 5000 PENBased(PENB) 10 16 10992 WDBc(WDB) 2 14 569 ADUlt(ADU) 2 14 48841 表 4 IK-D-TSK参数设置
数据集 分类器 规则数 数据字典 (WDB) 3 2~15 3~4 (WAV) 1.10~120
2.15~140
3.18~16017~20 (PENB) 10~13 (SAT) 5 1.5~90
2.8~120
3.10~150
4.13~170
5.15~19010~13 (ADU) 40~45 (MUS) 20~23 表 5 各分类器运行时间比较结果(s)
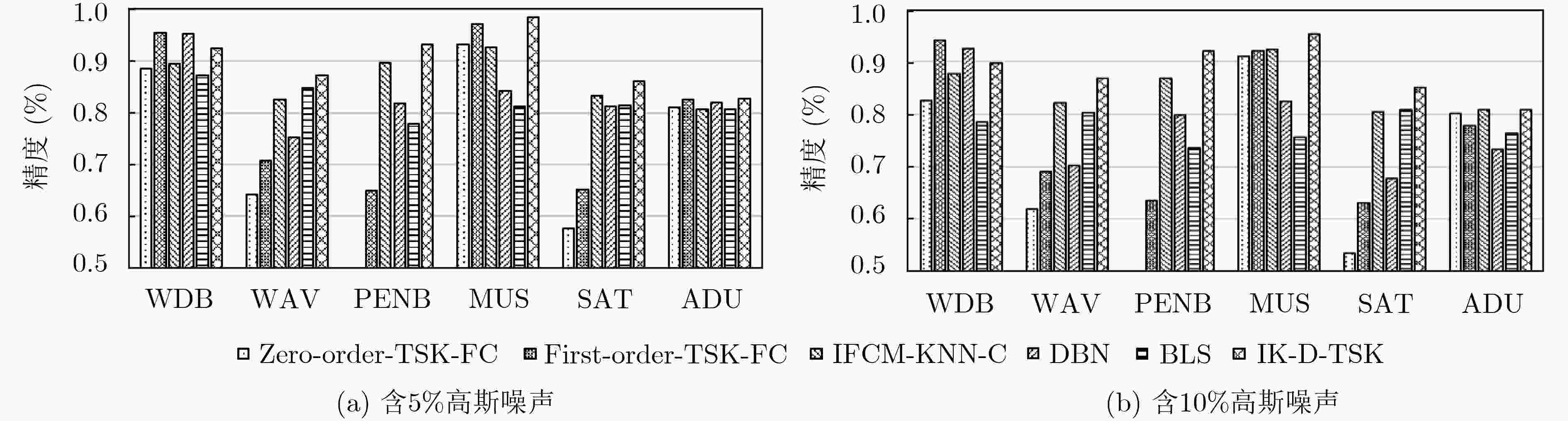
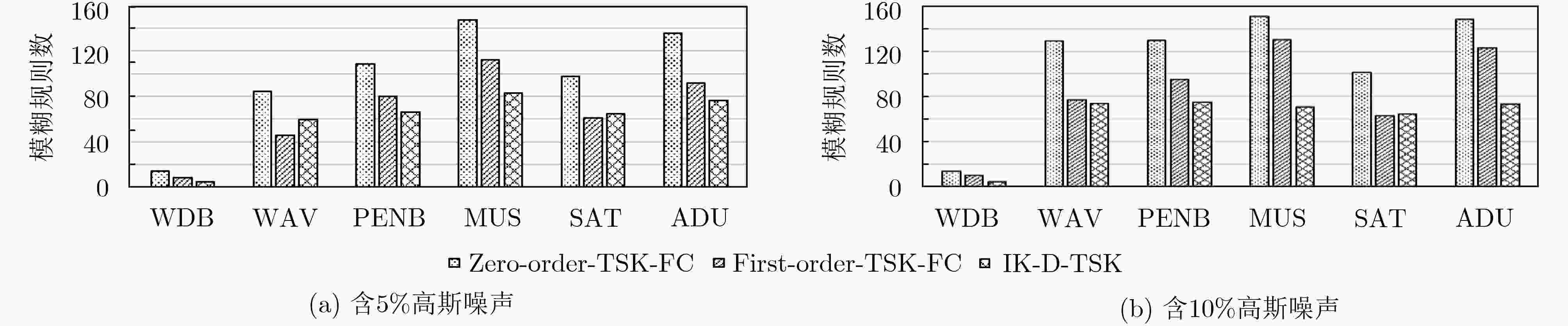
数据集 Zero-order-TSK-FC[1] First-order-TSK-FC[14] IFCM-KNN-C DBN[18] BLS[19] IK-D-TSK 5%噪音 10%噪音 5%噪音 10%噪音 5%噪音 10%噪音 5%噪音 10%噪音 5%噪音 10%噪音 5%噪音 10%噪音 训练时间 训练时间 训练时间 训练时间 训练时间 训练时间 训练时间 训练时间 训练时间 训练时间 训练时间 训练时间 测试时间 测试时间 测试时间 测试时间 测试时间 测试时间 测试时间 测试时间 测试时间 测试时间 测试时间 测试时间 WDB 0.0216
(0.0039)0.0224
(0.0057)0.0237
(0.0034)0.0243
(0.0023)0.0162
(0.0019)0.0141
(0.0018)4.1844
(0.1861)4.1555
(0.1592)0.0122
(0.0013)0.0122
(0.0011)0.0209
(0.0032)0.0205
(0.0023)0.0004 0.0005 0.0004 0.0004 0.0016 0.0016 0.0086 0.0079 0.0102 0.0104 0.0021 0.0020 WAV 0.7982
(0.0256)0.7984
(0.0346)3.8207
(0.0719)4.1065
(0.2303)0.2863
(0.0222)0.2808
(0.0181)35.4047
(0.2407)35.2445
(0.1511)0.0256
(0.0028)0.0261
(0.0016)0.3333
(0.0366)0.3130
(0.0409)0.0050 0.0071 0.0059 0.0112 0.0128 0.0129 0.0430 0.0391 0.0155 0.0170 0.0143 0.0142 PENB 0.9656
(0.0181)0.9794
(0.0320)3.7465
(0.1615)3.9261
(0.1764)0.5067
(0.0225)0.4809
(0.0151)15.1945
(0.1656)15.2313
(0.1790)0.0189
(0.0013)0.0191
(0.0012)0.6105
(0.0372)0.5659
(0.0323)0.0098 0.0097 0.0196 0.0224 0.0353 0.0311 0.0086 0.0086 0.0124 0.0125 0.0352 0.0340 MUS 0.9496
(0.0230)0.9965
(0.0377)7.6208
(0.2844)8.1693
(0.2367)0.8053
(0.0629)0.8124
(0.0223)47.1515
(0.2267)47.3102
(0.3248)0.0323
(0.0038)0.0321
(0.0032)0.9432
(0.0415)0.9513
(0.0323)0.0123 0.0125 0.0283 0.0361 0.0253 0.0231 0.0469 0.0602 0.0189 0.0187 0.0241 0.0244 SAT 1.2282
(0.0720)1.2301
(0.0738)13.3579
(0.4825)14.2199
(0.6745)0.3393
(0.0262)0.3221
(0.0134)338.383
(1.2035)346.9789
(4.4332)0.1491
(0.0052)0.1578
(0.0099)0.4881
(0.0441)0.4528
(0.0383)0.0073 0.0062 0.0167 0.0254 0.0183 0.0184 0.2492 0.2039 0.0644 0.0658 0.0209 0.0209 ADU 5.9016
(0.1901)6.0366
(0.1239)15.9947
(0.8757)17.3695
(0.8218)3.1255
(0.0415)3.0311
(0.0215)56.4922
(0.3625)64.3266
(0.6555)0.0337
(0.0028)0.0389
(0.0051)5.9502
(0.7296)5.5299
(0.5056)0.0322 0.0370 0.0768 0.1047 0.1126 0.1127 0.0305 0.0656 0.0200 0.0230 0.1549 0.1536 表 6 WDB数据集在IK-D-TSK上生成的数据字典
${{{ \upsilon }}_{1,1}} = [0.3221,0.6299,0.3633,0.3023,0.5487,0.5950,0.5260,0.3796,0.4162,0.4037,0.5162,0.2613,0.7203,0.4236, - 1]{\rm{ }}$ ${{{ \upsilon }}_{1,2}} = [0.3589,0.5702,0.3630,0.2741,0.5715,0.5258,0.5245,0.4388,0.4216,0.3926,0.4954,0.2346,0.5913,0.3333, - 1]{\rm{ }}$ ${{{ \upsilon }}_{1,3}} = [0.2962,0.5501,0.4035,0.2355,0.5358,0.5635,0.5233,0.4925,0.3430,0.3778,0.5045,0.4081,0.7043,0.5754, - 1]$ ${{{ \upsilon }}_{2,1}}{\rm{ = [}}0.3555,0.5604,0.3788,0.2586,0.5516,0.5644,0.5155,0.4579,0.4592,0.3885,0.5256,0.3284,0.5952,0.1384{\rm{,1]}}$ ${{{ \upsilon }}_{2,2}} = [0.3646,0.3985,0.2364,0.2755,0.4574,0.5489,0.4467,0.4598,0.3965,0.4276,0.4772,0.4100,0.4240,0.2729,1]$ ${{{ \upsilon }}_{2,3}} = [0.3582,0.6097,0.2785,0.3392,0.3736,0.6051,0.5651,0.4549,0.4203,0.3447,0.4312,0.4583,0.5412,0.1683,1]$ -
TEH C Y, KERK Y W, TAY K M, et al. On modeling of data-driven monotone zero-order TSK fuzzy inference systems using a system identification framework[J]. IEEE Transactions on Fuzzy Systems, 2018, 26(6): 3860–3874. doi: 10.1109/TFUZZ.2018.2851258 PEDRYCZ W and GOMIDE F. Fuzzy Systems Engineering: Toward Human-Centric Computing[M]. Hoboken, NJ: Wiley, 2007: 85–101. TAKAGI T and SUGENO M. Fuzzy identification of systems and its applications to modeling and control[J]. IEEE Transactions on Systems, Man, and Cybernetics, 1985, SMC-15(1): 116–132. doi: 10.1109/TSMC.1985.6313399 TAO Dapeng, CHENG Jun, YU Zhengtao, et al. Domain-weighted majority voting for crowdsourcing[J]. IEEE Transactions on Neural Networks and Learning Systems, 2019, 30(1): 163–174. doi: 10.1109/TNNLS.2018.2836969 HU Mengqiu, YANG Yang, SHEN Fumin, et al. Robust Web image annotation via exploring multi-facet and structural knowledge[J]. IEEE Transactions on Image Processing, 2017, 26(10): 4871–4884. doi: 10.1109/TIP.2017.2717185 ZHANG Yuanpeng, ISHIBUCHI H, and WANG Shitong. Deep Takagi-Sugeno-Kang fuzzy classifier with shared linguistic fuzzy rules[J]. IEEE Transactions on Fuzzy Systems, 2018, 26(3): 1535–1549. doi: 10.1109/TFUZZ.2017.2729507 CORDON O, HERRERA F, and ZWIR I. Linguistic modeling by hierarchical systems of linguistic rules[J]. IEEE Transactions on Fuzzy Systems, 2002, 10(1): 2–20. doi: 10.1109/91.983275 NASCIMENTO D S C, BANDEIRA D R C, CANUTO A M P, et al. Investigating the impact of diversity in ensembles of multi-label classifiers[C]. 2018 International Joint Conference on Neural Networks, Rio de Janeiro, Brazil, 2018: 1–8. doi: 10.1109/IJCNN.2018.8489660. BISHOP C M. Pattern Recognition and Machine Learning[M]. New York: Springer, 2006: 51–75. 王士同, 钟富礼. 最小学习机[J]. 江南大学学报: 自然科学版, 2010, 9(5): 505–510. doi: 10.3969/j.issn.1671-7147.2010.05.001WANG Shitong and CHUNG K F L. On least learning machine[J]. Journal of Jiangnan University:Natural Science Edition, 2010, 9(5): 505–510. doi: 10.3969/j.issn.1671-7147.2010.05.001 TUR G, DENG Li and HAKKANI-TÜR D, et al. Towards deeper understanding: Deep convex networks for semantic utterance classification[C]. 2012 IEEE International Conference on Acoustics, Speech and Signal Processing, Kyoto, Japan, 2012: 5045-5048. doi: 10.1109/ICASSP.2012.6289054. WOLPERT D H. Stacked generalization[J]. Neural Networks, 1992, 5(2): 241–259. doi: 10.1016/s0893-6080(05)80023-1 ZADEH L A. Fuzzy sets[J]. Information and Control, 1965, 8(3): 338–353. doi: 10.1016/S0019-9958(65)90241-X DENG Zhaohong, JIANG Yizhang, CHUNG F L, et al. Knowledge-leverage-based fuzzy system and its modeling[J]. IEEE Transactions on Fuzzy Systems, 2013, 21(4): 597–609. doi: 10.1109/TFUZZ.2012.2212444 GU Xin, CHUNG F L, ISHIBUCHI H, et al. Multitask coupled logistic regression and its fast implementation for large multitask datasets[J]. IEEE Transactions on Cybernetics, 2015, 45(9): 1953–1966. doi: 10.1109/TCYB.2014.2362771 BACHE K and LICHMAN M. UCI machine learning repository[EB/OL]. http://archive.ics.uci.edu/ml, 2015. ALCALÁ-FDEZ J, FERNÁNDEZ A, LUENGO J, et al. KEEL data-mining software tool: Data set repository, integration of algorithms and experimental analysis framework[J]. Journal of Multiple-Valued Logic & Soft Computing, 2011, 17(2/3): 255–287. HINTON G E, OSINDERO S, and TEH Y W. A fast learning algorithm for deep belief nets[J]. Neural Computation, 2006, 18(7): 1527–1554. doi: 10.1162/neco.2006.18.7.1527 CHEN C L P and LIU Zhulin. Broad learning system: An effective and efficient incremental learning system without the need for deep architecture[J]. IEEE Transactions on Neural Networks and Learning Systems, 2018, 29(1): 10–24. doi: 10.1109/TNNLS.2017.2716952 -





 下载:
下载:


 下载:
下载:
