Error Analysis of Dynamic Sea Surface Height Measurement by Near-nadir Interferometric SAR
-
摘要:
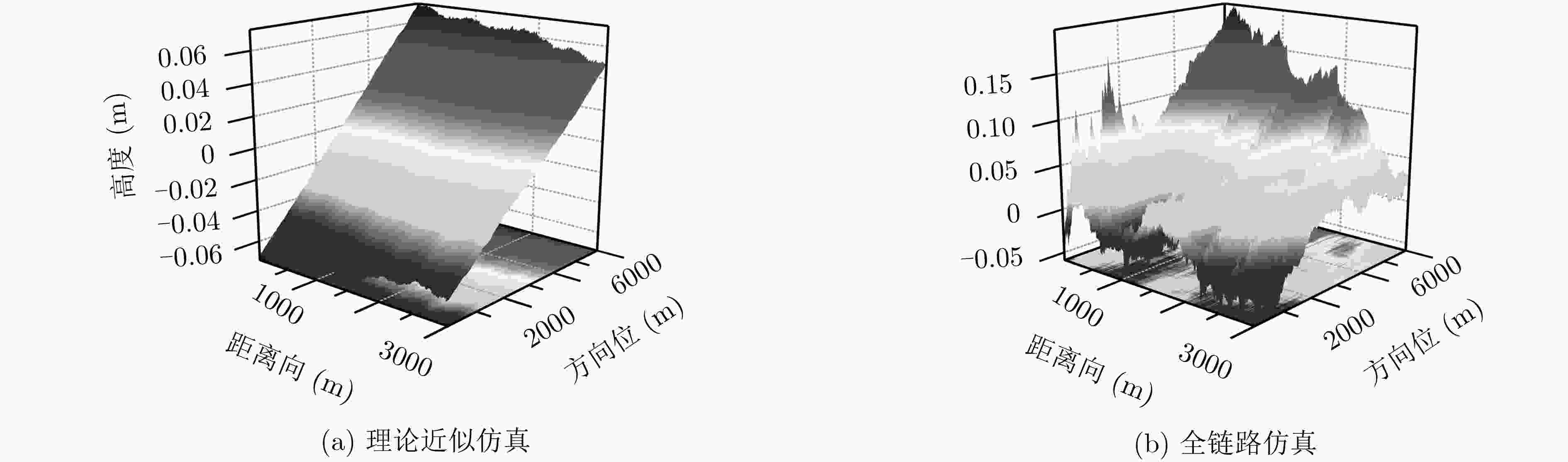
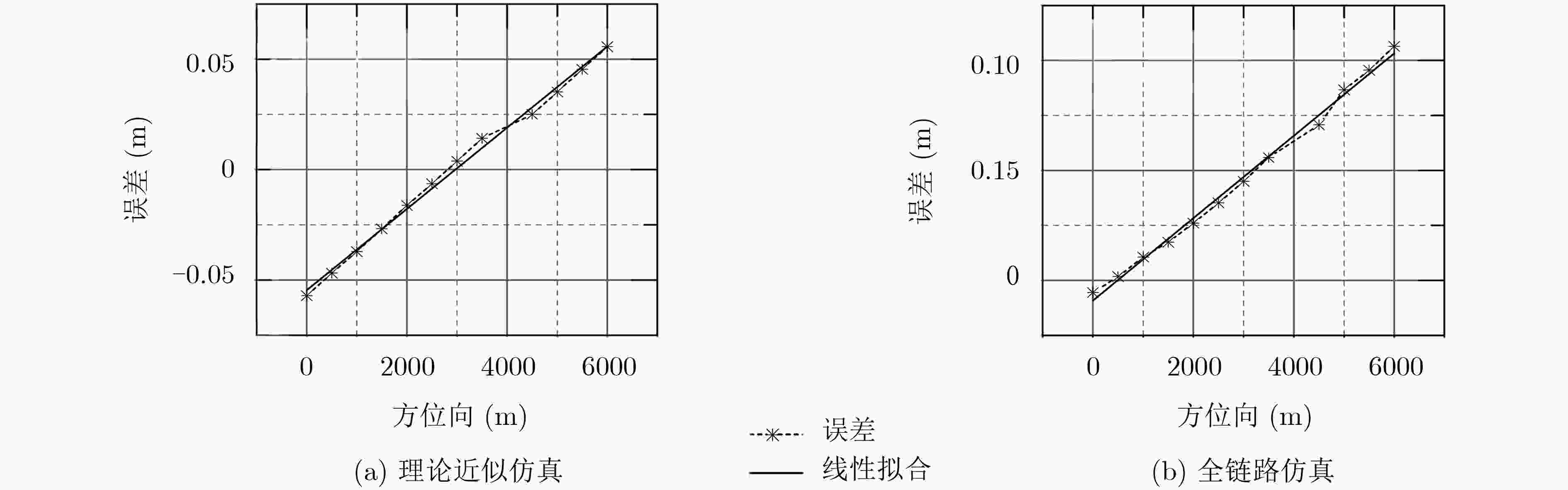
采用近天底的宽刈幅干涉高度计是近年来新发展的海面高程测量技术,与陆地高程测量不同,海浪一直处于随机运动之中,其动态特性会在合成孔径雷达(SAR)成像和干涉处理中引入显著误差。对于厘米级的干涉测量精度要求来说,该误差是主要误差源之一。该文研究了由海面特性引起的高程误差机理及其对于近天底干涉SAR测高精度的影响,建立了运动误差理论模型,同时考虑了电磁偏差与叠掩偏差影响。基于不同SAR工作体制,在不同海况下进行了理论近似仿真,并进行了干涉SAR全链路仿真,全链路仿真结果能够与理论仿真较好地吻合,验证了误差模型的正确。结果显示由海浪引起的误差随着多普勒中心频率近似呈线性变化,且与目标散射加权径向速度成正比。误差不仅与海浪特性相关,还与雷达系统参数相关,这能为未来系统设计、误差预算和海面高程处理提供参考。
Abstract:The wide-swath interferometric altimeter working at near-nadir is a newly developed ocean surface topography measurement technology in recent years. Different from land elevation measurement, for the dynamic ocean surface waves, they move randomly all the time and this brings bias in Synthetic Aperture Radar (SAR) imaging and interferometric processes and leads to the final height measurement errors. For the requirement of centimeter-level precision, this error is the main source of measurement errors. The errors due to the characteristics of ocean surface and their impact on near-nadir InSAR’s precision are investigated. The motion error theoretical model is established combining the characteristics of the ocean surface and InSAR working mechanism, and the electromagnetic bias and layover bias are also taken into consideration. The error models in different SAR modes under various sea states are simulated. The error model is validated by the interferometric SAR full-link experimental simulation and the simulation results are consistent with the theoretical values. The results show that the errors are approximately linear changing with the Doppler centroid frequency and are proportional to the radial velocity of targets modulated by scattering. The errors are not only related to the characteristics of the waves, but also related to system parameters. This work can provide the feasible suggestions for future system design, error budget and data processing.
-
Key words:
- InSAR /
- Sea surface height /
- Error budget /
- Targets motion
-
表 1 理论仿真系统参数
仿真系统参数 参数值 平台高度 800 km 基线 10 m 中心频率 Ka波段 极化方式 HH 入射角 4°~4.7° 距离采样率 0.8 m 方位采样率 5 m 距离分辨率 1 m 方位分辨率 50 m 表 2 条带模式下误差RMS
海况 RMS(cm) 低海况 0.2670 中等海况 1.3154 高海况 6.6361 表 3 TOPS模式下误差RMS
海况 RMS(cm) 低海况 1.9598 中等海况 2.2621 高海况 6.9801 表 4 实验验证系统参数
实验系统参数 参数值 平台高度 852 km 基线 12 m 中心频率 Ka波段 极化方式 HH 入射角 9°~12° 带宽 65 MHz 脉冲重复频率 3005 Hz 距离分辨率 3 m 方位分辨率 15 m -
FU L L and CAZENAVE A. Satellite Altimetry and Earth Sciences: A Handbook of Techniques and Applications[M]. San Diego: Academic Press, 2001: 11–12. ZAWADZKI L and ABLAIN M. Accuracy of the mean sea level continuous record with future altimetric missions: Jason-3 vs. Sentinel-3a[J]. Ocean Science, 2016, 12(1): 9–18. doi: 10.5194/os-12-9-2016 VAZE P, KAKI S, LIMONADI D, et al. The surface water and ocean topography mission[C]. 2018 IEEE Aerospace Conference, Big Sky, USA, 2018: 1–9. doi: 10.1109/AERO.2018.8396504. FJØRTOFT R, GAUDIN J M, POURTHIÉ N, et al. KaRIn on SWOT: Characteristics of near-nadir Ka-band interferometric SAR imagery[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(4): 2172–2185. doi: 10.1109/TGRS.2013.2258402 ESTEBAN F D, POLLARD B V P, and ABELSON R. SWOT project mission performance and error budget[R]. JPL, NASA, 2017. ZHANG Yunhua, SHI Xiaojin, WANG Hongjian, et al. Interferometric imaging radar altimeter on board Chinese Tiangong-2 Space Laboratory[C]. 2018 Asia-Pacific Microwave Conference, Kyoto, Japan, 2018: 851–853. doi: 10.23919/APMC.2018.8617189. KONG Weiya, CHONG Jinsong, and TAN Hong. Performance analysis of ocean surface topography altimetry by Ku-band near-nadir interferometric SAR[J]. Remote Sensing, 2017, 9(9): 933–947. doi: 10.3390/rs9090933 PERAL E, RODRÍGUEZ E, and ESTEBAN-FERNÁNDEZ D. Impact of surface waves on SWOT’s projected ocean accuracy[J]. Remote Sensing, 2015, 7(11): 14509–14529. doi: 10.3390/rs71114509 ROSEN P A, HENSLEY S, JOUGHIN I R, et al. Synthetic aperture radar interferometry[J]. Proceedings of the IEEE, 2000, 88(3): 333–382. doi: 10.1109/5.838084 PIRES N, FERNANDES M J, GOMMENGINGER C, et al. Improved sea state bias estimation for altimeter reference missions with altimeter-only three-parameter models[J]. IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(3): 1448–1462. doi: 10.1109/tgrs.2018.2866773 DUBOIS P and CHAPRON B. Characterization of the ocean waves signature to assess the Sea State Bias in wide-swath interferometric altimetry[C]. 2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 2018: 3789–3792. doi: 10.1109/IGARSS.2018.8518813. CHEN Yao, WANG Xiaoqing, HUANG Mo, et al. Analysis of the sea state bias in interferometric radar altimeter[C]. 2018 China International SAR Symposium, Shanghai, China, 2018: 1–7. doi: 10.1109/SARS.2018.8551968. PERRY R P, DIPIETRO R C, and FANTE R L. SAR imaging of moving targets[J]. IEEE Transactions on Aerospace and Electronic Systems, 1999, 35(1): 188–200. doi: 10.1109/7.745691 ROMEISER R, ALPERS W, and WISMANN V. An improved composite surface model for the radar backscattering cross section of the ocean surface: 1. Theory of the model and optimization/validation by scatterometer data[J]. Journal of Geophysical Research: Oceans, 1997, 102(C11): 25237–25250. doi: 10.1029/97jc00190 APEL J R. An improved model of the ocean surface wave vector spectrum and its effects on radar backscatter[J]. Journal of Geophysical Research: Oceans, 1994, 99(C8): 16269–16291. doi: 10.1029/94jc00846 余颖, 王小青, 朱敏慧, 等. 基于二阶散射的海面三尺度雷达后向散射模型[J]. 电子学报, 2008, 36(9): 1771–1775. doi: 10.3321/j.issn:0372-2112.2008.09.022YU Ying, WANG Xiaoqing, ZHU Minhui, et al. Three-scale radar backscattering model of the ocean surface based on second-order scattering[J]. Acta Electronica Sinica, 2008, 36(9): 1771–1775. doi: 10.3321/j.issn:0372-2112.2008.09.022 MANCON S, GUARNIERI A M, GIUDICI D, et al. On the phase calibration by multisquint analysis in TOPSAR and stripmap interferometry[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(1): 134–147. doi: 10.1109/TGRS.2016.2598686 -





 下载:
下载:



 下载:
下载:
