Quantization and Energy Optimization Strategy of Wireless Sensor Networks
-
摘要:
由于无线传感网络(WSN)存在能量和带宽的限制,在网络中直接传送模拟信号受到了极大地制约,因此对模拟信号量化是节省网络能量和保证有效带宽的重要手段。为此,该文以融合中心的重构绝对均值误差最小为原则,设计一种网络量化及能量优化方法。首先,针对单传感器,在能量固定的情况下推导了最优量化位数及在量化位数固定的情况下推导了最优能量分配。其次,在单传感器的基础上,进一步推导多传感器情况下最优量化位数及最优能量分配。以上两种情况都考虑了传感器测量噪声及信道衰落损耗。最后,通过数值仿真方法验证了文中所提方法的正确性,并将其与等能量分配进行了比较,获得了较好的效果。
Abstract:Due to the limitation of energy and bandwidth in Wireless Sensor Networks(WSN), the direct transmission of analog signals in the network is greatly restricted. Therefore, quantization of analog signals is an important means to save network energy and ensure effective bandwidth. To this end, based on the principle of minimum absolute mean reconstruction error a network quantization and energy optimization method is designed in this paper. Firstly, for single sensor, the optimal quantization bit number is derived under the condition of fixed energy and the optimal energy distribution is derived under the condition of fixed quantization bit number. Secondly, on the basis of single sensor, the optimal quantization bit number and optimal energy allocation are further deduced in multi-sensor case. In both cases, the sensor measurement noise and channel fading loss are considered. Finally, the numerical simulation results show that the proposed method is correct and better than the equal energy distribution.
-
Key words:
- Wireless Sensor Networks(WSN) /
- Optimal power allocating /
- Quantization /
- Cluster-based
-
刘伟, 杜佳鸿, 贾素玲, 等. 能量有效的无线传感器网络分簇路由协议[J]. 北京航空航天大学学报, 2019, 45(1): 50–56. doi: 10.13700/j.bh.1001-5965.2018.0251LIU Wei, DU Jiahong, JIA Suling, et al. Energy efficient clustering routing protocol for wireless sensor networks[J]. Journal of Beijing University of Aeronautics and Astronautics, 2019, 45(1): 50–56. doi: 10.13700/j.bh.1001-5965.2018.0251 ALVI A N, BOUK S H, AHMED S H, et al. BEST-MAC: Bitmap-assisted efficient and scalable TDMA-based WSN MAC protocol for smart cities[J]. IEEE Access, 2016, 4: 312–322. doi: 10.1109/ACCESS.2016.2515096 QUINTERO V, PEREZ A, ESTEVEZ C, et al. State-of-charge estimation to improve decision making by MAC protocols used in WSNs[J]. Electronics Letters, 2019, 55(3): 161–163. doi: 10.1049/el.2018.7666 张聚伟, 王宇, 杨挺. 基于数据融合的有向传感器网络全覆盖部署[J]. 传感技术学报, 2017, 30(1): 139–145. doi: 10.3969/j.issn.1004-1699.2017.01.025ZHANG Juwei, WANG Yu, and YANG Ting. Full coverage deployment algorithm of directional sensor network based on data fusion[J]. Chinese Journal of Sensors and Actuators, 2017, 30(1): 139–145. doi: 10.3969/j.issn.1004-1699.2017.01.025 ZHANG Senlin, CHEN Huayan, LIU Meiqin, et al. Optimal quantization scheme for data-efficient target tracking via UWSNs using quantized measurements[J]. Sensors, 2017, 17(11): 2565–2584. doi: 10.3390/s17112565 ZHANG Linxia, NIU Dunbiao, SONG Enbin, et al. Joint optimization of dimension assignment and compression in distributed estimation fusion[J]. IEEE Transactions on Signal Processing, 2019, 67(9): 2453–2468. doi: 10.1109/TSP.2019.2904935 CHEN Bo, ZHANG Wenan, and YU Li. Distributed finite-horizon fusion Kalman filtering for bandwidth and energy constrained wireless sensor networks[J]. IEEE Transactions on Signal Processing, 2014, 62(4): 797–812. doi: 10.1109/tsp.2013.2294603 GUO Xiaoxi, LEONG A S, and DEY S. Estimation in wireless sensor networks with security constraints[J]. IEEE Transactions on Aerospace and Electronic Systems, 2017, 53(2): 544–561. doi: 10.1109/TAES.2017.2649178 郭黎利, 高飞, 孙志国. 无线传感器网络中基于多比特量化的极大似然分布式估计方法[J]. 电子学报, 2016, 44(11): 2773–2779. doi: 10.3969/j.issn.0372-2112.2016.11.029GUO Lili, GAO Fei, and SUN Zhiguo. Multi-level quantization scheme for distributed maximum likelihood estimation in wireless sensor networks[J]. Acta Electronica Sinica, 2016, 44(11): 2773–2779. doi: 10.3969/j.issn.0372-2112.2016.11.029 王瑛, 邹芳, 王飞雪, 等. 多次观测信号检测的最优量化[J]. 电子学报, 2008, 36(3): 575–580. doi: 10.3321/j.issn:0372-2112.2008.03.032WANG Ying, ZOU Fang, WANG Feixue, et al. Optimum quantization for multi-observation signal detection[J]. Acta Electronica Sinica, 2008, 36(3): 575–580. doi: 10.3321/j.issn:0372-2112.2008.03.032 BLUM R S. Asymptotically optimum quantization with time invariant breakpoints for signal detection[J]. IEEE Transactions on Information Theory, 1991, 37(2): 402–407. doi: 10.1109/18.75265 ZHOU Yan, LI Jianxun, and WANG Dongli. Target tracking in wireless sensor networks using adaptive measurement quantization[J]. Science China Information Sciences, 2012, 55(4): 827–838. doi: 10.1007/s11432-011-4327-3 LEE J. Optimal power allocating for correlated data fusion in decentralized WSNs using algorithms based on swarm intelligence[J]. Wireless Networks, 2017, 23(5): 1655–1667. doi: 10.1007/s11276-017-1454-9 MOHAJERZADEH A H, YAGHMAEE M H, and FAKOOR V. Total data collection algorithm based on estimation model for wireless sensor network[J]. Wireless Personal Communications, 2015, 81(2): 745–778. doi: 10.1007/s11277-014-2156-6 LEE E A and MESSERSCHMITT D G. Digital Communication[M]. Boston: Kluwer Academic, 1988. KAY S M. Fundamentals of Statistical Signal Processing, Volume Ⅲ: Practical Algorithm Development[M]. Englewood Cliffs: Prentice Hall, 2013: 415–416. SRIPAD A and SNYDER D. A necessary and sufficient condition for quantization errors to be uniform and white[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1977, 25(5): 442–448. doi: 10.1109/TASSP.1977.1162977 -





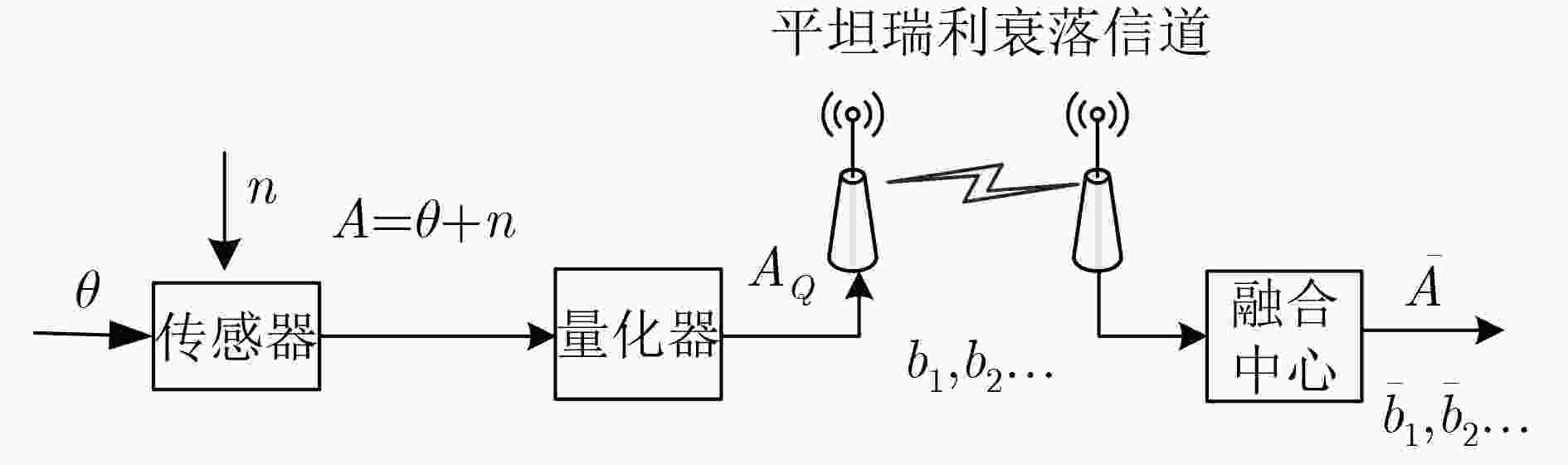
 下载:
下载:
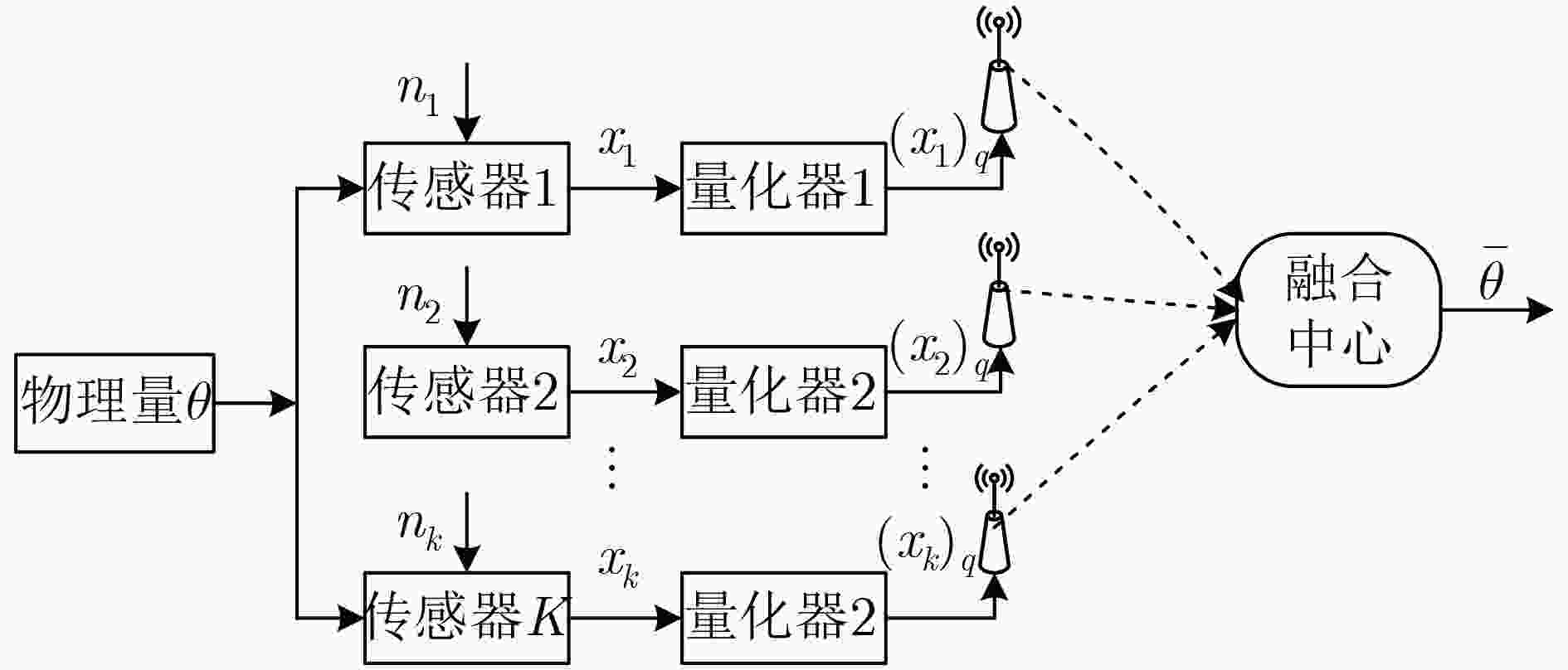
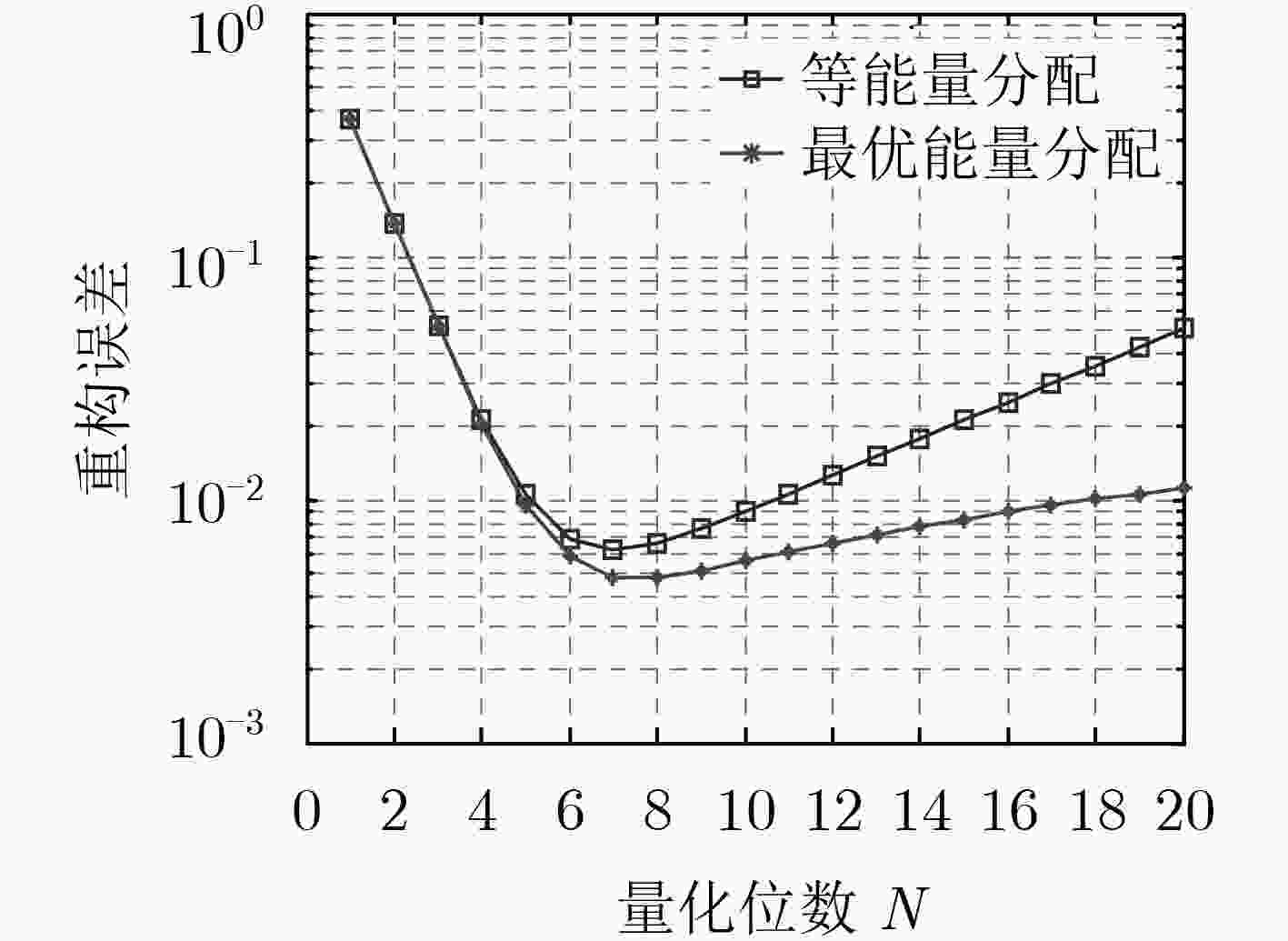
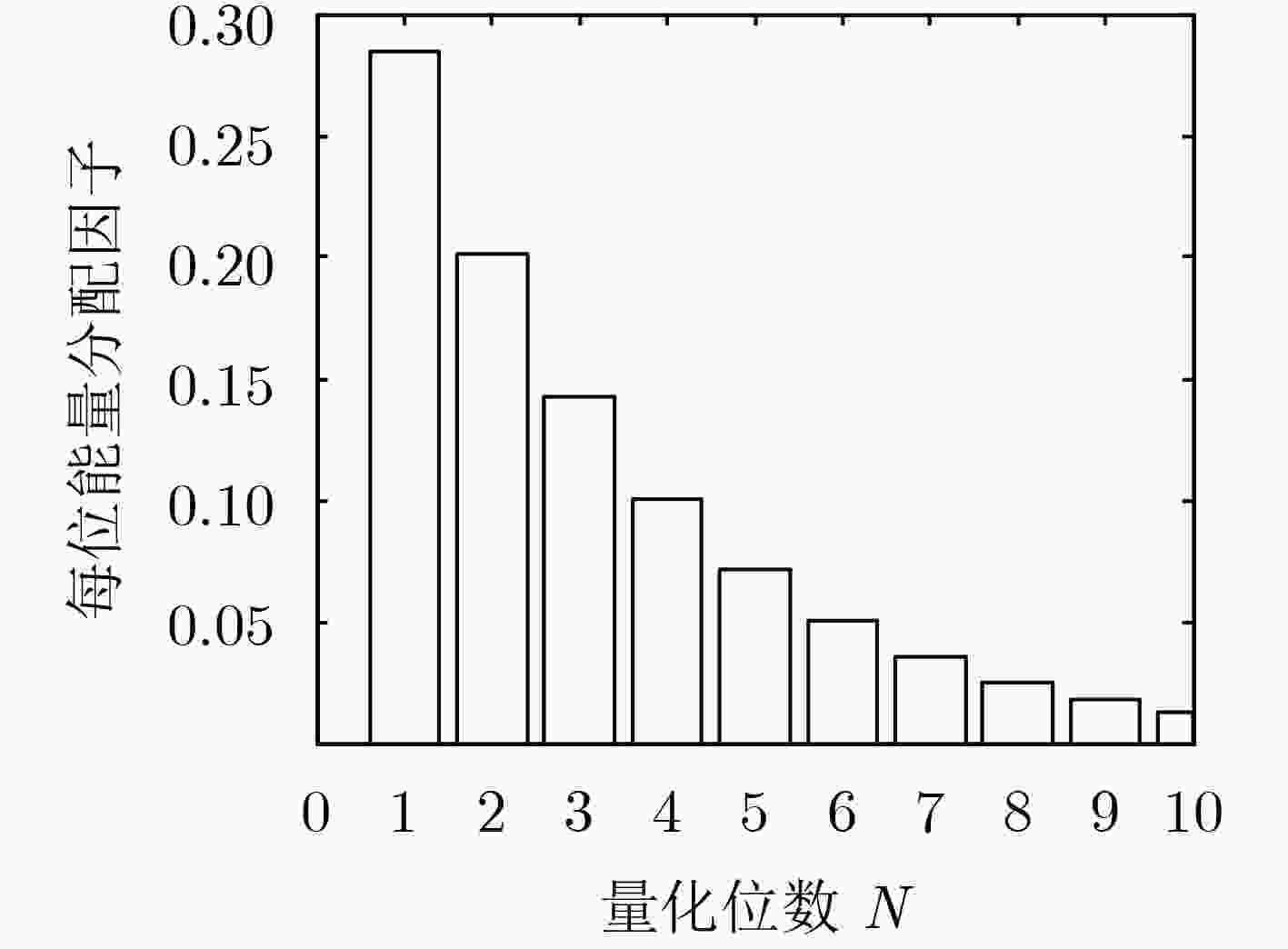


 下载:
下载:
