一种针对大型凹型障碍物的组合导航算法

李庆华; 尤越; 沐雅琪; 张钊; 冯超

doi:10.11999/JEIT190179

一种针对大型凹型障碍物的组合导航算法

doi: 10.11999/JEIT190179

李庆华^{1, 4},
尤越^{2, 4},
沐雅琪^{2, 4},
张钊²,
冯超^{1, 3, 4, ,}

1.
齐鲁工业大学(山东省科学院)电子信息工程学院(大学物理教学部) 济南 250353
2.
齐鲁工业大学(山东省科学院)电气工程与自动化学院济南 250353
3.
齐鲁工业大学(山东省科学院)山东省科学院自动化研究所济南 250101
4.
济南市人机智能协同工程实验室济南 250353

基金项目: 国家自然科学基金(61701270)，齐鲁工业大学(山东省科学院)青年博士合作基金(2017BSHZ008)

详细信息

作者简介:
李庆华：男，1977年生，副教授，研究方向为信号与信息处理

尤越：女，1996年生，硕士生，研究方向为智能路径规划

沐雅琪：女，1996年生，硕士生，研究方向为复杂环境路径规划算法

张钊：男，1995年生，硕士生，研究方向为人工智能运动目标行为识别

冯超：男，1984年生，讲师，研究方向为路径规划运动规划

通讯作者:
冯超　cfeng@qlu.edu.cn

中图分类号: TN96
计量
- 文章访问数: 2614
- HTML全文浏览量: 1298
- PDF下载量: 86
- 被引次数: 14
出版历程
- 收稿日期: 2019-03-26
- 修回日期: 2019-11-10
- 网络出版日期: 2019-11-13
- 刊出日期: 2020-06-04

Integrated Navigation Algorithm for Large Concave Obstacles

Qinghua LI^{1, 4},
Yue YOU^{2, 4},
Yaqi MU^{2, 4},
Zhao ZHANG²,
Chao FENG^{1, 3, 4
, ,}

1.
School of Electronic and Information Engineering (Department of Physics), Qilu University of Technology (Shandong Academy of Sciences), Jinan 250353, China)
2.
School of Electrical Engineering and Automation, Qilu University of Technology (Shandong Academy of Sciences), Jinan 250353, China
3.
Institute of Automation, Qilu University of Technology (Shandong Academy of Sciences), Jinan 250101, China
4.
Jinan Engineering Laboratory of Human-machine Intelligent Cooperation, Jinan 250353, China

Funds: The National Natural Science Foundation of China (61701270), The Young Doctor Cooperation Foundation of Qilu University of Technology (Shandong Academy of Sciences) (2017BSHZ008)

摘要

摘要:
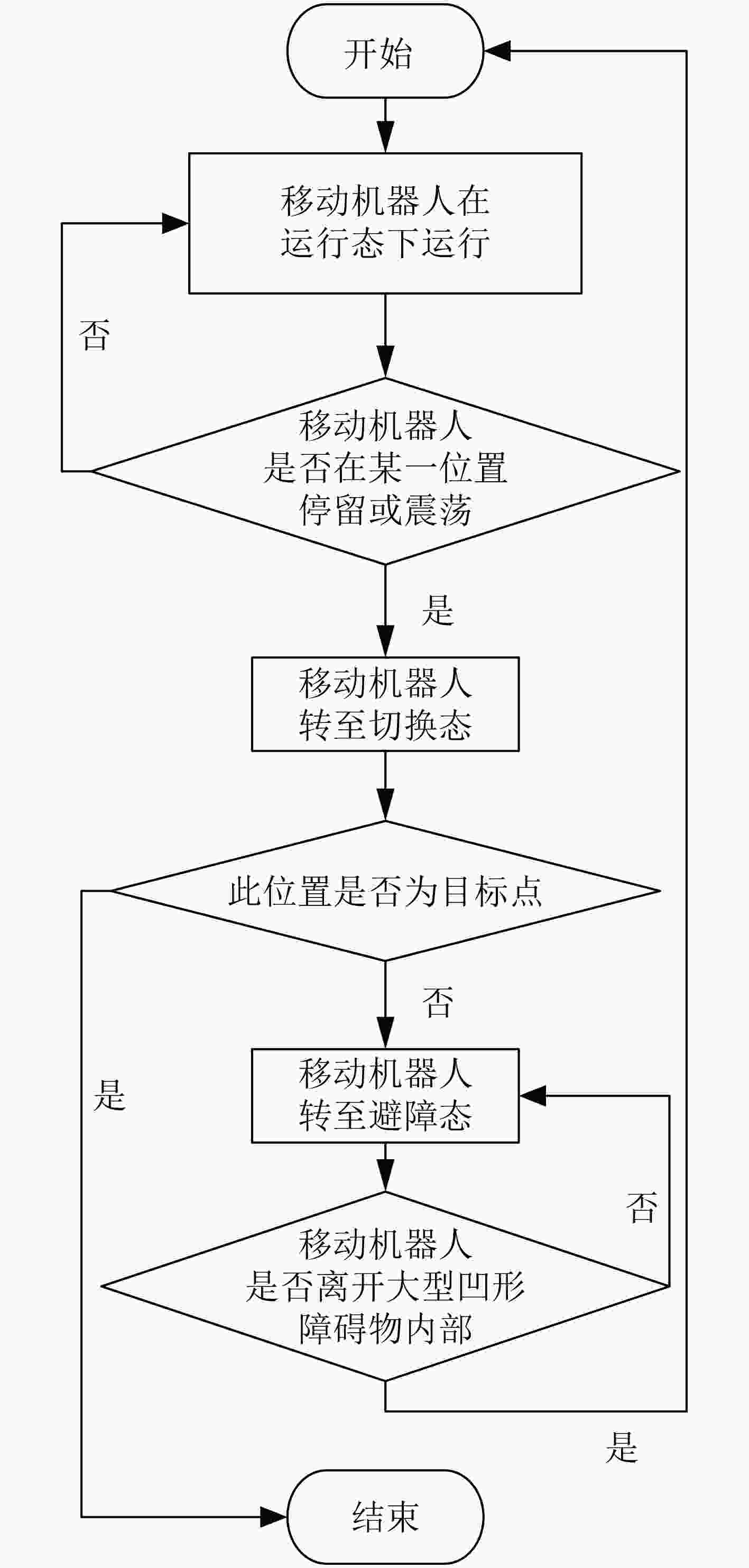
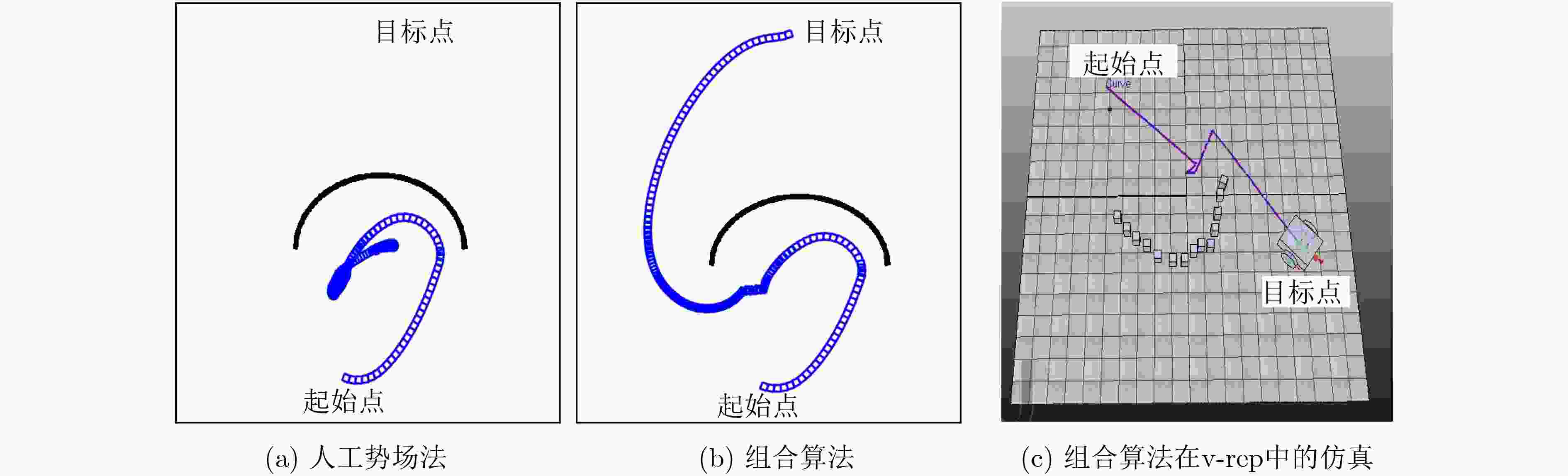
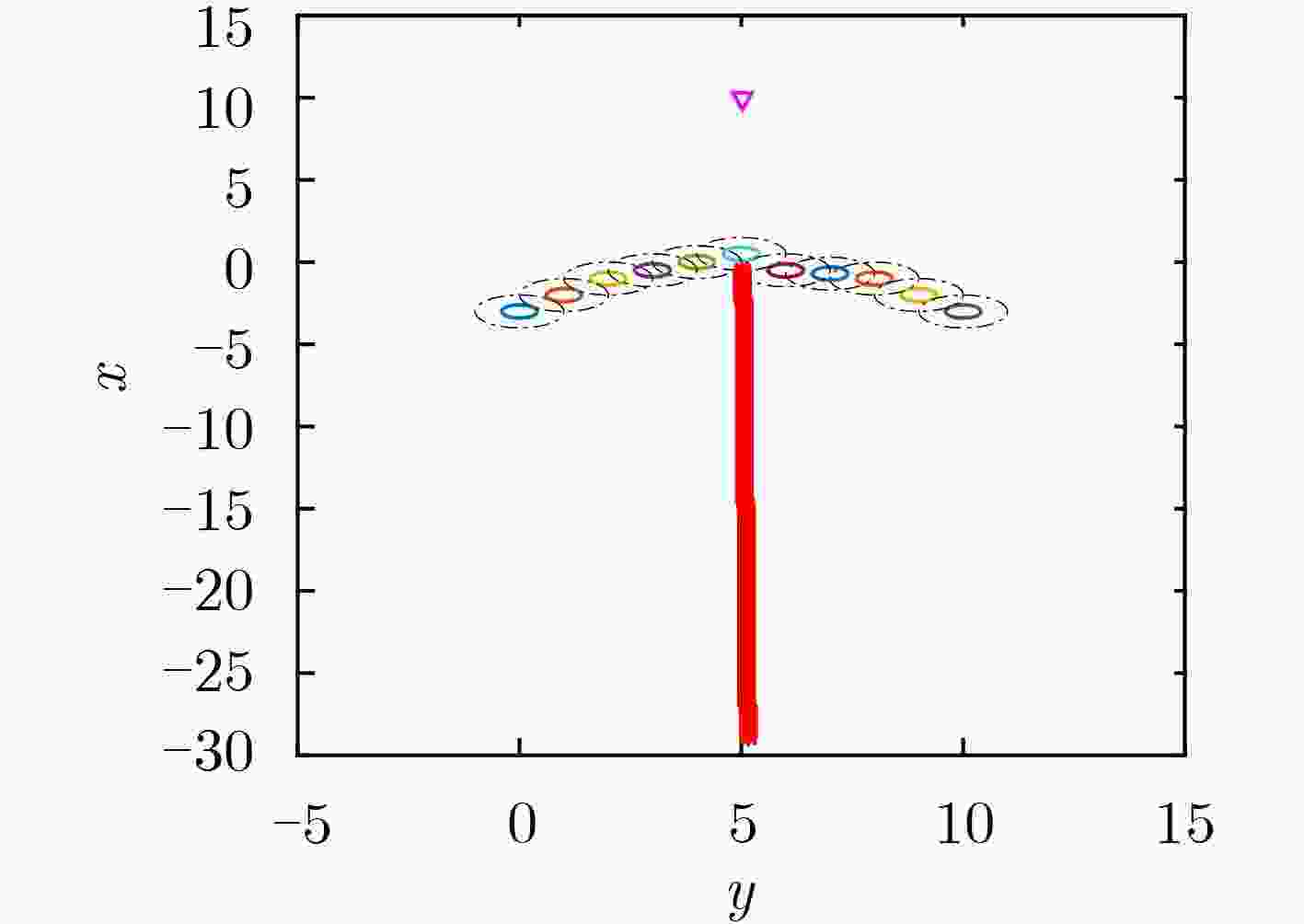
针对移动机器人导航过程中无法规避大型凹型障碍物问题，该文提出一种多状态的组合导航算法。算法按照不同的运动环境，将移动机器人的运行状态分类为运行态、切换态、避障态，同时定义了基于移动机器人运行速度和运行时间的状态双切换条件。当移动机器人处于运行态时，采用人工势场法(APFM)进行导航，并实时观测毗邻障碍物的几何构型。在遭遇障碍物时，切换态用于判断是否满足状态切换条件，以进入避障态执行避障算法。避障完成后，状态自动切换回运行态继续执行导航任务。多状态的提出，可有效解决传统人工势场法在大型凹形障碍物的避障过程中存在局部震荡的问题。基于运行速度和运行时间的双切换条件判定算法，可实现多状态间的平滑切换。实验结果表明，该算法在解决局部震荡问题的同时，还可降低避障时间，提升导航算法效率。
- 组合导航算法 /
- 人工势场法 /
- A*算法 /
- 大型凹形障碍物
Abstract:
For the problem that mobile robot can not avoid large concave obstacles during navigation, this paper proposes a multi-state integrated navigation algorithm. The algorithm classifies the running state of mobile robot into running state, switching state and obstacle avoidance state according to different moving environment, and defines the state double switching conditions based on the running speed and running time of the mobile robot. The Artificial Potential Field Method (APFM) is used to navigate and observe the geometric configuration of adjacent obstacles in real time. When encountering an obstacle, the switching state is used to determine whether the state switching condition is satisfied, and the obstacle avoidance algorithm is executed to enter the obstacle avoidance state and enter the obstacle avoidance state to implement the obstacle avoidance algorithm. After the obstacle avoidance is completed, the state automatically switches back to the running state to continue the navigation task. The proposal of multi-state can solve the problem of local oscillation of traditional artificial potential field method in the process of avoiding large concave obstacles. Furthermore, the double-switching condition determination algorithm based on running speed and running time can realize smooth switching between states and optimize the path. The experimental results show that the algorithm can not only solve the local oscillation problem, but also reduce the obstacle avoidance time and improve the efficiency of the navigation algorithm.
- Integrated navigation algorithm /
- Artificial Potential Field Method (APFM) /
- A* algorithm /
- Large concave obstacle

HTML全文

1. 引言

词语是中文文本中包含语义信息并且能够独立使用的最小结构单元，因此中文分词(Chinese Word Segmentation, CWS)是中文自然语言处理(Natural Language Processing, NLP)的基础，其性能好坏将对NLP下游任务的效果产生直接影响。

早期的中文分词方法主要包括机械分词法^[1]和统计分词法^[2,3]两种。机械分词法需要预先构造一个足够大的中文词表，然后通过设置词表中词语的组合规则来对中文句子进行切分。统计分词法则是根据相邻字之间的共现频率来计算它们构成词语的可信度，无需预先构建词表。由于这两种方法所使用的分词模型都较为简单，不能很好地描述复杂的中文构词规律，因此分词性能并不理想。随着深度学习技术的提出和发展，近年来提出了多种利用深度神经网络来进行中文分词的方法^[4,5]。与传统的分词方法不同，基于深度神经网络的分词方法将中文分词当成序列标注任务，以人工标注的数据集来训练网络，在无需获取中文词表和人为构造规则，也不需要人为构造特征模板的情况下，利用深度网络的强大建模能力，能获得远高于传统方法的准确率(Precision)和召回率(Recall)，因此成为目前中文分词的主流技术。

在基于深度神经网络的中文分词方法中，首先需要使用大量标注好的语料来训练网络模型，然后利用训练好的网络模型对无标注的测试语料进行分词。当训练语料的领域(源领域)与测试语料的领域(目标领域)属于同一个领域时，这种方法能通常能取得很好的效果，但当源领域和目标领域不属于同一个领域，即跨领域(cross domain)时，其性能将会显著降低。造成这种现象的原因主要有两个，一是未登录词(Out Of Vocabulary, OOV)，即目标领域中存在着大量未在源领域中出现过的词语，这些词语对于网络模型来说是未知样本，难以正确识别。另一个原因是领域之间的表达鸿沟，即不同领域的语言表达是有差异的，使得网络模型在源领域上学习的特征对于目标领域并不具有很好的泛化性能。解决未登录词和表达鸿沟最简单的方法是对目标领域的语料进行标注并重新训练模型，但由于在实际中对所有未知领域的训练语料进行人工标注需要非常高的成本，并不可行，因此如何有效地解决中文分词系统的领域适应性，特别是未登录词和表达鸿沟问题，是目前中文分词的最大难点之一。现有的研究中，在模型的训练中结合词典或字/词向量是解决未登录词的最常用的方法^[6]，而迁移学习则是解决表达鸿沟的主要方法^[7]。尽管目前对跨领域中文分词中的未登录词或表达鸿沟问题已有一定的研究，但现有的文献所提方法大多只针对两者之一，而同时解决两个问题的研究成果尚不多见。

本文针对跨领域中文分词中的未登录词和表达鸿沟问题，首先采用现有技术构建了一个基于新词发现的跨领域中文分词系统，实现了自动从目标领域语料中提取新词、标注语料和训练网络模型的功能。然后针对现有新词发现算法提取出的词表垃圾词串多的缺点，提出了一种基于向量增强互信息和加权邻接熵的无监督新词发现算法，以提高新词词表提取的准确率和领域性。最后，针对自动标注语料中存在噪声样本的不足，提出了一种基于对抗式训练的中文分词模型，有效提高了分词网络模型训练的鲁棒性。

文章的其余部分组织如下：第2节介绍了本文搭建的基线系统，第3节提出了基于向量增强互信息和加权邻接熵的无监督新词发现算法，第4节提出了基于对抗式训练的中文分词算法，第5节是实验结果和分析，最后一节给出了结论。

2. 基线系统

为了同时处理跨领域分词中的未登录词和表达鸿沟问题，本文构建的基线系统包含新词发现、自动标注和跨领域分词3个部分，结构如图1所示。首先使用新词发现算法从各个目标领域语料中提取出该领域的新词词表，然后利用该新词词表对无标注的目标领域语料进行自动标注，以降低目标领域语料的未登录词率，最后使用自动标注好的语料训练分词模型，并使用该模型来对目标领域进行分词。在这个系统中，新词发现能显著减少跨领域分词中的未登录词率，而对目标领域语料的自动标注并在此基础上训练适用于目标领域的分词模型，则能有效解决跨领域分词中的表达鸿沟问题。

图 1 基线系统的结构

下载: 全尺寸图片幻灯片

新词发现包含语料预处理、候选词提取和候选词过滤3个步骤。目标领域的中文语料首先按照非中文字符的方式进行切割，并剔除非汉字字符，然后使用N-Gram的方法^[8]从目标领域语料中提取出所有的候选字符串，得到候选词集。此时得到的候选词集既包含了正确的词语，又包含了大量错误的字符组合，因此需要对词集中的词进行筛选。互信息(Mutual Information, MI)和邻接熵(Branch Entropy, BE)相结合的方法是目前最常用的词集筛选方法^[9]，首先统计每个候选词在目标领域语料中的词频后，然后采用下式计算出每个词的得分

${\text{score}}\left( {{\boldsymbol{w}}} \right) = {{\rm{MI}}} \left( {{\boldsymbol{w}}} \right) + \min \left( {{{H}_{\text{l}}}({{\boldsymbol{w}}}),{{H}_{\text{r}}}({w})} \right)$

(1)

其中

${\text{MI}}\left( {{\boldsymbol{w}}} \right) = \mathop {\min }\limits_{_{1 \le i < n}} \ln \frac{{p\left( {{\boldsymbol{w}}} \right)}}{{p\left( {{c_1}{c_2} \cdots {c_i}} \right) \cdot p\left( {{c_{i + 1}} \cdots {c_n}} \right)}}$

(2)

为互信息， ${{\boldsymbol{w}}} = {c_1}{c_2} \cdots {c_i}{c_{i + 1}} \cdots {c_n}$ 为长度为 $n$ 的候选词， ${c_i}$ 为 ${{\boldsymbol{w}}}$ 中的第 $i$ 个字符， $p\left( \cdot \right)$ 表示在语料中出现的概率。 ${H_{\text{l}}}\left( {{\boldsymbol{w}}} \right)$ 和 ${H_{\text{r}}}\left( {{\boldsymbol{w}}} \right)$ 分别为候选词 ${{\boldsymbol{w}}}$ 的左邻接熵和右邻接熵，定义为

${H_{\text{l}}}\left( {{\boldsymbol{w}}} \right) = - \sum\limits_{i = 1}^k p \left( {{l_i}} \right) \cdot \ln \left( {p\left( {{l_i}} \right)} \right)$

(3)

${H_{\text{r}}}\left( {{\boldsymbol{w}}} \right) = - \sum\limits_{i = 1}^{{k^\prime }} p \left( {{r_i}} \right) \cdot \ln \left( {p\left( {{r_i}} \right)} \right)$

(4)

其中

$p\left( {{l_i}} \right) = \frac{{N\left( {{l_i}} \right)}}{{\displaystyle\sum\limits_{j = 1}^k N\left( {{l_j}} \right)}}$

(5)

$p\left( {{r_i}} \right) = \frac{{N\left( {{r_i}} \right)}}{{\displaystyle\sum\limits _{j = 1}^{k'} N\left( {{r_j}} \right)}}$

(6)

$p\left( {{l_i}} \right)$ 表示左邻接字 ${l_i}$ 出现的概率， $N\left( {{l_i}} \right)$ 和 $N\left( {{l_j}} \right)$ 为字符 ${l_i}$ 和 ${l_j}$ 在字片段 ${w}$ 左侧出现的次数， $p\left( {{r_i}} \right)$ 表示右邻接字 ${r_i}$ 出现的概率， $N\left( {{r_i}} \right)$ 和 $N\left( {{l_j}} \right)$ 为字符 ${r_i}$ 和 ${r_j}$ 在字片段 ${w}$ 右侧出现的次数， $k$ 和 $k'$ 分别表示左邻接字和右邻接字的数量。过滤掉得分较低的候选词，并剔除源领域词表中的词和中文常用词，即可得到一个干净的目标领域新词词表。

自动标注中，首先根据目标领域的新词词表使用逆向最大匹配算法(Backward Maximum Matching, BMM)^[10]对目标领域语料进行初步的切分，然后利用有标注的源领域语料训练分词模型，并使用该模型对目标领域的语料进行完全切分，得到自动标注的目标领域语料。分词模型是中文分词系统的核心，由于目前基于深度神经网络的分词方法均将中文分词当成序列标注任务，因此主流的中文分词方法是使用双向长短时记忆网络(Bidirectional Long Short-Term Memory, BiLSTM)^[11]加上条件随机场模型(Conditional Random Fields, CRF)^[12]。由于在BiLSTM中，输入之间相互依赖使得模型在处理当前字符时还可以提取到上下文里的语境和语义信息，并且从理论上来说这个上下文可以扩展到全文，而CRF模型属于统计模型，可以在分词模型中加入有关于语料的统计信息，能很好地弥补深度模型无法提取浅层特征的劣势，因此BiLSTM+CRF在领域内分词和跨领域分词中都取得了很好的效果。但BiLSTM在实际使用中存在着训练速度慢、信息冗余，在获取远距离依赖时容易出现梯度爆炸或者梯度弥散的缺点。为此，本文的基线系统中使用了门控卷积神经网络(Gated Convolutional Neural Network, GCNN)^[13]来代替BiLSTM。GCNN是带有线性门控的卷积神经网络，使用线性门控后能令模型在堆叠获取远距离上下文时可以遗忘不重要的信息而只保留重要的信息，远距离依赖效果将会变得更好，不仅可以进一步降低梯度弥散的现象，还可以保留CNN的非线性能力。

跨领域分词时，利用自动标注好的目标领域语料训练出一个适用于目标领域的GCNN-CRF模型，即可以使用该模型对目标领域内的测试语料进行分词。由于该模型是使用自动标注好的目标领域语料训练出来的，因此能克服跨领域中文分词的未登录词和表达鸿沟问题。

3. 基于向量增强互信息和加权邻接熵的无监督新词发现算法

传统基于MI+BE的无监督新词发现算法认为互信息可以表示字符串内部聚合度的大小，左右邻接熵可以表示字符串边界自由度的高低，因此将互信息和邻接熵直接相加可以同时衡量字符串内部聚合度和边界自由度的高低。但在实验中发现，使用MI+BE算法提取的新词词表中存在大量垃圾词串，例如“过程中”、“线城市”等非词语的固定搭配由于具有较大的词频和互信息，并且邻接熵也较大，很容易被错误地认为是一个合理的新词。究其原因，MI+BE算法一方面在判定内部凝结度上只利用了语料中的统计信息，使得一些常用搭配因为凝固度较高而被认为也是新词，另一方面在判定边界自由度上只利用了左右邻接熵中的较小值，使得一些错误词串也被认为是新词，造成提取出的新词词表中含有较多的垃圾词串。本文针对MI+BE算法的不足，提出了基于向量增强互信息和加权邻接熵的无监督新词发现算法。

3.1 向量增强互信息

对于一个新词而言，它内部的片段应该是紧密结合并且很大概率是一起出现在句子中的，也就是说这些片段之间必然就会有着相似的上下文语境，因此使用上下文语境的相关性来进一步描述字符串内部的结合程度对新词发现应有一定的帮助。本文借助基于语义的词向量来对互信息进行改进，提出向量增强互信息(Vector Enhancement Mutual Information, VEMI)的概念。

假设将候选词 ${{\boldsymbol{w}}} = {c_1}{c_2} \cdots {c_i}{c_{i + 1}} \cdots {c_n}$ 分成两个字符片段 ${c_1}{c_2} \cdots {c_i}$ 和 ${c_{i + 1}} \cdots {c_n}$ ，其向量表达为 ${{\bf{Vec}}_{{c_1}{c_2} \cdots {c_i}}} = \left( {{a_1},{a_2}, \cdots ,{a_n}} \right)$ 和 ${{\bf{Vec}}_{{c_{i + 1}} \cdots {c_n}}} = \left( {{b_1},{b_2}, \cdots ,{b_n}} \right)$ ，定义它们的余弦相似度为

${\rm{simCos}} = \frac{{\displaystyle\sum\limits_{i = 1}^n {{a_i}} \cdot {b_i}}}{{\sqrt {\left( {\displaystyle\sum\limits_{i = 1}^n {a_i^2} } \right)\left( {\displaystyle\sum\limits_{i = 1}^n {b_i^2} } \right)} }}$

(7)

将余弦相似度作为相关性的另一个计算因素加入到 ${\rm{MI}}\left( {{\boldsymbol{w}}} \right)$ 中，得到向量增强互信息为

$\begin{split} {\rm{VEMI}}\left( {{\boldsymbol{w}}} \right) =& \mathop {\min }\limits_{_{1 \le i < n}} \ln \frac{{p\left( {{\boldsymbol{w}}} \right)}}{{p\left( {{c_1}{c_2} \cdots {c_i}} \right)p\left( {{c_{i + 1}} \cdots {c_n}} \right)}} \\ & + \alpha \cdot {\rm{simCos}} \end{split}$

(8)

其中， $\alpha$ 是一个超参数，用于平衡互信息和语义相似性的重要性。在VEMI的计算中加入字符片段的余弦相似度，使其输出不但受字符片段结合的紧密度影响，还考虑了上下文的相关性，因此应当优于传统的MI准则。

由于字符片段 ${c_1}{c_2} \cdots {c_i}$ 和 ${c_{i + 1}} \cdots {c_n}$ 不一定是一个合理的词，在实际中难以直接通过常规的词向量训练得到它们的向量 ${{\bf{Vec}}_{{c_1}{c_2} \cdots {c_i}}}$ 和 ${{\bf{Vec}}_{{c_{i + 1}} \cdots {c_n}}}$ ，因此本文采用的方法是先将语料切分为字符，然后使用Word2Vec^[14]模型进行训练得到所有字符对应的字向量，这些字向量中即包含有一定范围内的上下文语义信息，最后将得到的字向量进行相加求平均得到字符片段的向量。设任意字符 ${c_j}$ 通过Word2Vec训练得到的字向量为 ${{\bf{Vec}}_{{c_j}}} = \left( {{a_{j1}},{a_{j2}}, \cdots ,{a_{jn}}} \right)$ ，则字符片段 ${c_1}{c_2} \cdots {c_i}$ 的向量采用下式计算

${{\bf{Vec}}_{{c_1}{c_2} \cdots {c_i}}} = \frac{1}{i}\sum\limits_{j = 1}^i {{{\bf{Vec}}_{{c_j}}}}$

(9)

3.2 加权邻接熵

根据式(3)和式(4)计算得到字符片段的左右邻接熵后，传统的方法是选择较小的熵作为指标来对字片段的边界进行衡量，这种方式虽然简单，但是并没有充分考虑到左右两边的邻接熵信息，在很多情况下是不合适的，例如候选词语“红皮病”，由于其在文中多是单独成句子出现，因此其左邻接熵很低，传统的算法会将这个词语剔除，但“红皮病”在文本中却是一个新词。为此，本文对传统的邻接熵进行了改进，采用加权的方式来同时利用左右两边的邻接熵信息，加权邻接熵的计算为

$\begin{split} {\rm{BE}}\left( {{\boldsymbol{w}}} \right) =& {H_{\text{l}}}\left( {{\boldsymbol{w}}} \right) \cdot \ln \frac{{{H_{\text{r}}}\left( {{\boldsymbol{w}}} \right)}}{{\left| {{H_{\text{l}}}\left( {{\boldsymbol{w}}} \right) - {H_{\text{r}}}\left( {{\boldsymbol{w}}} \right)} \right| + \varepsilon }} \\ & + {H_{\text{r}}}\left( {{\boldsymbol{w}}} \right) \cdot \ln \frac{{{H_{\text{l}}}\left( {{\boldsymbol{w}}} \right)}}{{\left| {{H_{\text{l}}}\left( {{\boldsymbol{w}}} \right) - {H_{\text{r}}}\left( {{\boldsymbol{w}}} \right)} \right| + \varepsilon }} \end{split}$

(10)

其中， ${\rm{BE}}\left( {{\boldsymbol{w}}} \right)$ 表示加权后的邻接熵， ${H_{\rm{l}}}\left( {{\boldsymbol{w}}} \right)$ 和 ${H_{\rm{r}}}\left( {{\boldsymbol{w}}} \right)$ 分别为词 ${{\boldsymbol{w}}}$ 的左邻接熵和右邻接熵， $\varepsilon$ 为一个小的正数。式(10)的对数部分相当于对左右邻接熵加上一个权重，其作用主要有两个方面，一是令较大的熵权值变小，较小的熵权值变大，从而使最终结果不再仅由其中的较小值所支配；二是当一个字符串片段的左右邻接熵都比较小，但相差不大时，有很大可能是一个合理的词，式(10)会增加这种情况下左右熵的权重，使得总得分变大。以“关节病”这个片段为例，实验中统计得到其左邻字分别有{疗，对}，出现次数依次为{1，1}，右邻字分别有{人，或，的}，出现的次数依次为{8, 1, 1}。据统计得到的左右邻字及其出现次数，可以得到其左右邻接熵分别为0.693和0.639，选择其中较小的右邻熵作为得分，则得分过小，“关节病”这个片段将不会认为是一个合理的新词。而根据式(10)可以计算得到其邻接熵为3.341，这是一个较大的熵值，会认为这个片段是一个合理的新词。由此可见，使用加权邻接熵比直接使用左右邻接熵中的较小值进行判断效果更好。

3.3 候选词筛选

通过N-Gram方法切分语料得到了所有长度不大于预设值的候选字符串片段，并使用Word2Vec训练目标领域语料中的汉字，得到了目标领域语料中所有汉字的字向量后，采用向量增强互信息和加权邻接熵来对所有的候选词 ${{\boldsymbol{w}}}$ 进行打分

${\text{score}}\left( {{\boldsymbol{w}}} \right) = \sigma \left( {a \cdot N\left( {{\rm{VEMI}}\left( {{\boldsymbol{w}}} \right)} \right) + b \cdot N\left( {{\rm{BE}}\left( {{\boldsymbol{w}}} \right)} \right)} \right)$

(11)

其中， $\sigma$ 为 ${{\rm{sigmoid}}}$ 函数， $N\left( \cdot \right)$ 表示最大最小值归一化

$N\left( {f\left( {{\boldsymbol{w}}} \right)} \right) = \frac{{{f_{\max }} - f\left( {w} \right)}}{{{f_{\max }} - {f_{\min }}}}$

(12)

${f_{\max }}$ 和 ${f_{\min }}$ 为 $f\left( {{\boldsymbol{w}}} \right)$ 的最大和最小值，系数 $a$ 和 $b$ 分别表示互信息和邻接熵在最终得分中所占据的权重大小。计算出候选词的得分后，剔除得分小于阈值的候选词。

经过得分筛选后，第2步将进行词频筛选。一个片段如果是一个合理的词语，那么这个片段在语料必然是多次出现的，本文将词频的最小值设定为8，出现次数小于8的片段即使得分较大也不认为是一个合理的词，将其从候选词中删除。

通过观察发现，采用以上步骤得到的新词词表中仍然存在少量诸如“导致了”、“扩展到”等错误词语，因此本文对词表进行了第3次筛选：统计候选词的首字和尾字的出现次数，如果这些字出现的次数大于一定值就认为这些字构成的词属于常用搭配而不是新词，比如“了”就在首尾中出现了261次，高于预设的阈值100，那么认为这些词语就是不合理的新词将其进行删除。

需要注意的是，由于分词只是将合理的词切分出来，不涉及词语语义的理解，因此中文的同义词只要是正确的词，组成它们的字之间的互信息以及它们与邻近字之间的联系与其他正确词语具有相似的特性，同样可以采用本文方法进行切分，无需特殊处理。

4. 基于对抗式训练的中文分词模型

尽管本文提出的新词发现算法提取出的新词词表具有较高的准确性和领域性，但目标领域语料是完全基于新词词表和分词算法进行自动标注的。由于词表和分词算法本身并不能保证完全正确，因此自动标注的语料会存在着一定数量的噪声样本。基线系统中使用的GCNN-CRF算法原本是基于正确标注好语料而设计的，并未考虑到训练语料中会存在噪声，因此并不具有抑制噪声对模型影响的能力，自动标注语料中的噪声将会影响分词模型的性能。针对这个问题，本文提出了一种基于对抗式训练的中文分词模型，通过单独提取出源领域和目标领域的共有特征来提高目标领域特征的鲁棒性，其结构如图2所示。

图 2 基于对抗式训练的中文分词模型

下载: 全尺寸图片幻灯片

由图2可以看到，本文提出的跨领域分词模型包含3个GCNN编码器，分别是源领域GCNN编码器、目标领域GCNN编码器和共享GCNN编码器。源领域编码器和目标领域编码器只接收各自领域的文本作为输入，用于提取各自领域独有特征，共享编码器则同时接收两个领域的文本作为输入，提取两个领域的共有特征。源领域编码器得到的独有特征和共享编码器得到的共有特征组合即可得到源领域的文本特征，再将这个特征输入到CRF中对源领域的文本预测词位标签。目标领域的处理方式与源领域相同。共享编码器的目标是尽可能提取出源领域和目标领域共有的特征，文中采用了对抗式训练来对其进行优化，将共享编码器中提取出的共有特征输入到一个文本判别器TextCNN^[15]中，使用文本判别器来判别共享编码器输出的特征是来自源领域还是目标领域。

模型训练时，上支路和中间支路、下支路和中间支路的训练交替进行，即源领域编码器和目标领域编码器的参数交替更新，共享编码器和文本判别器的参数每次迭代都更新。假设句子 ${{{\boldsymbol{s}}}_{\text{s}}}$ 和 ${{{\boldsymbol{s}}}_{\text{t}}}$ 分别来自源领域和目标领域，它们通过源领域编码器、目标领域编码器和共享编码器后分别得到源领域的独有特征 ${{{\boldsymbol{H}}}_{\text{s}}}$ 、目标领域的独有特征 ${{{\boldsymbol{H}}}_{\text{t}}}$ 和两个领域的共有特征 ${{{\boldsymbol{H}}}^*}$ 。 ${{{\boldsymbol{H}}}^*}$ 提取越准确，其领域性就越低，文本判别器就越难通过它判别句子来自哪个领域，可以据此对共享编码器和文本判别器进行对抗式训练。将 ${{{\boldsymbol{H}}}^*}$ 输入文本判别器的TextCNN，TextCNN将产生一个 ${{{\boldsymbol{H}}}^*}$ 属于源领域或目标领域的概率，令 $G\left( {{{H}^*}} \right)$ 表示TextCNN的输出，文本判别器总损失函数设置为

$L_{\text{s}}^* = {{ - }}{{\text{E}}_{\text{s}}}\left[ {\lg \left( {G\left( {{{{\boldsymbol{H}}}^*}} \right)} \right)} \right]{{ - }}{{\text{E}}_{\text{s}}}\left[ {{\text{lg}}\left( {1 - G\left( {{{{\boldsymbol{H}}}^{\text{*}}}} \right)} \right)} \right]$

(13)

$L_{\text{t}}^* = {{ - }}{{\text{E}}_{\text{t}}}\left[ {\lg \left( {G\left( {{{{\boldsymbol{H}}}^*}} \right)} \right)} \right]{{ - }}{{\text{E}}_{\text{t}}}\left[ {{\text{lg}}\left( {1 - G\left( {{{{\boldsymbol{H}}}^{\text{*}}}} \right)} \right)} \right]$

(14)

其中， $L_{\text{s}}^{\text{*}}$ 为文本判别器在上支路和中间支路训练时的损失函数， ${{{\rm{E}}} _s}\left[ \cdot \right]$ 表示对源领域的句子求期望， $L_{\text{t}}^{\text{*}}$ 为文本判别器在下支路和中间支路训练时的损失函数， ${{{\rm{E}}} _{\text{t}}}\left[ \cdot \right]$ 表示对目标领域的句子求期望。源领域和目标领域的总损失函数 $L_{\text{s}}^{{\text{total}}}$ 和 $L_{\text{t}}^{{\text{total}}}$ 分别设置为

$L_{\text{s}}^{{\text{total}}} = {L_{\text{s}}} + \alpha \cdot {L_{\text{t}}} + L_{\text{s}}^{\text{*}}$

(15)

$L_{\text{t}}^{{\text{total}}} = {L_{\text{s}}} + \alpha \cdot {L_{\text{t}}} + L_{\text{t}}^{\text{*}}$

(16)

其中， ${L_{\text{s}}}$ 和 ${L_{\text{t}}}$ 分别为源领域编码器和目标领域编码器GCNN的交叉熵损失函数， $\alpha$ 为权重因子。考虑到目标领域中的文本是自动标注的，其中有不正确标注的样本，目标领域中的样本在训练中的置信度应该低于源领域，因此设置 $0 < \alpha < 1$ 。

通过共享编码器和文本判别器的对抗式训练，可以使共享编码器提取的特征包含更少的源领域和目标领域的独有特征，越来越接近两个领域的共有特征。与单个GCNN-CRF相比，本文方法有以下优势：(1)由于源领域的语料是正确标注的，因此两个领域的共有特征在理想情况下不含噪声，目标领域中的标注噪声只存在于其独有特征中。将目标领域的共有特征和独有特征分离，可以将噪声的影响限制在一定范围内，从而提高目标领域分词对标注错误的鲁棒性。(2)将源领域损失与目标领域损失的和作为总损失，与原GCNN-CRF模型相比相当于在训练过程中加入了正则化，可以起到防止过拟合和增强鲁棒性的作用。

5. 实验结果及分析

5.1 实验设置

实验中采用的数据分为源领域和目标领域两个部分，其中源领域数据为中文分词领域中普遍使用的北大开源新闻语料^[16]，目标领域数据包括医疗、小说《诛仙》和《斗罗》、发明专利3个领域的语料，这些目标领域语料中都随机选取一部分做了人工标注作为测试集，其中训练集和测试集的比例大致为5:1。各个数据集的大小如表1所示。

表 1 实验中使用的语料大小(Byte)

语料	句子(k)	词语(M)	字符(M)
新闻	53.7	1.3	2.1
医疗	32.0	0.7	1.2
《诛仙》	59.0	2.1	3.0
《斗罗》	40.0	2.0	0.9
发明专利	17.0	0.6	0.9

下载: 导出CSV

| 显示表格

实验中所使用的深度神经网络的训练和识别均基于开源框架tensorflow1.14，所有数据的编码格式为UTF-8，GCNN网络维度为200，层数为5，Dropout率为0.2，学习率为0.001，Epoch数为15。新词发现中的使用N-Gram方法切分的字符串片段最大长度为6，候选词得分阈值为0.95，词频阈值为8，首字和尾字的出现次数阈值为100。以上阈值均为经验阈值，通过观察和实验来确定。字符串最大长度、词频阈值、首字和尾字出现次数阈值分别通过观察统计训练语料分词结果中正确词语的长度、词频、典型的首字和尾字(如上文提到的“了”字)出现次数得到，这些阈值设置过严容易导致正确的词语被切分开或丢弃，而设置过宽松则容易产生错误的字词组合。候选词得分阈值则是在实验中尝试多个阈值后，选取未登录词率最优的0.95。

实验中对新词发现和中文分词算法的性能采用了不同的评价指标。新词发现算法的主要目的是用于解决跨领域中文分词中的未登录词问题，因此实验中使用未登录词率(即未登录词数量与总词数的比值)来作为评价指标。中文分词算法的性能则采用了准确率、召回率和F值(F-measure)3个常用的评价指标来衡量。

5.2 新词发现

为了衡量本文提出的新词发现算法的性能，实验中首先分别使用MI+BE算法和本文提出的新词发现算法从目标领域训练语料上提取该领域相对源领域语料独有的新词，再利用新词词表对目标领域测试语料进行自动标注，并统计标注过程中出现的未登录词占总词数的比例。实验中还对不进行新词发现、直接使用源领域词表对目标领域测试语料进行自动标注时的未登录词率进行了统计。表2给出了无新词发现、MI+BE算法和本文提出的新词发现算法应用于目标领域测试语料时的未登录词率。由表2的结果可以看出，使用了新词发现算法的未登录词率比无新词发现、直接使用源领域词表时有显著的下降，同时，本文所提的新词发现算法要明显优于传统的MI+BE算法，在各个语料上都取得了最好的效果，说明了本文方法的有效性。

表 2 不同方法的未登录词率(%)

算法	无新词发现	MI+BE	本文方法
医疗	25.93	16.31	5.42
《诛仙》	15.52	8.24	1.43
《斗罗》	11.15	7.06	1.23
发明专利	18.39	11.27	3.45

下载: 导出CSV

| 显示表格

为了更好地检验本文算法所提取的新词的合理性，表3给出了MI+BE算法和本文算法从各个语料中提取的前20个最频繁出现词中垃圾词串的数目。由表3可以看到，本文方法提取的词表更准确，有效地减少了词表中无意义的垃圾词串数量。

表 3 前20个最频繁出现词中垃圾词串数(个)

语料	医疗	《诛仙》	《斗罗》	发明专利
MI+BE	4	5	7	6
本文方法	1	1	2	6

下载: 导出CSV

| 显示表格

5.3 基于对抗式训练的分词算法

为了测试本文提出的基于对抗式训练的分词算法的效果，表4给出了GCNN-CRF与本文对抗式训练模型在目标领域测试语料上分词的准确率、召回率和F值，其中基线系统使用了MI+BE的新词发现算法和GCNN-CRF分词算法，GCNN-CRF使用了本文的新词发现算法和GCNN-CRF分词算法，本文方法使用了本文的新词发现算法和对抗式训练模型。由表4可以看到，基线系统的性能最差，使用了本文新词发现算法的GCNN-CRF性能次之，本文方法性能最优，这说明：(1)由于传统的MI+BE算法提取的新词词表中存在着较多的缺失和错误，本文的新词发现算法能更准确地提取新词，因此使用了本文新词发现算法的GCNN-CRF性能显著优于基线系统。(2)由表3可知，本文的新词发现算法中仍存在着少量标注错误的噪声样本，而在中文分词中引入对抗式训练可以有效地降低噪声样本对模型的影响，使模型在跨领域分词时取得比传统GCNN-CRF更高的准确率。

表 4 基于对抗式训练的分词算法效果

性能指标	准确率(%)			召回率(%)			F值
算法	基线	GCNN_CRF	本文方法	基线	GCNN_CRF	本文方法	基线	GCNN_CRF	本文方法
医疗	71.7	80.7	82.4	74.3	82.0	83.7	73.0	81.4	83.0
《诛仙》	77.8	89.3	90.3	75.6	87.5	87.7	76.7	88.4	89.0
《斗罗》	81.7	92.1	92.8	81.7	91.9	92.4	81.0	92.0	92.6
发明专利	84.3	88.1	89.8	81.6	87.1	87.2	82.9	87.6	88.5

下载: 导出CSV

| 显示表格

5.4 与现有方法的对比

为了衡量本文方法的整体性能，实验中将本文方法与文献[6]所提的方法进行了对比。文献[6]提出的分词模型首先采用人工识别的方法提前获得目标领域词典，然后将该领域词典作为先验知识和源领域标注语料组成训练集，通过训练改进的BiLSTM+CRF网络模型实现跨领域分词。由于本文所用的目标领域语料没有现成的人工标注词典，因此文献[6]的方法中人工词典使用本文的新词发现算法构造的词典代替。从表5可以看到，本文方法的性能显著优于文献[6]的方法。

表 5 本文方法与现有方法的性能对比

性能指标	准确率(%)			召回率(%)			F值
算法	基线系统	文献[6]	本文方法	基线系统	文献[6]	本文方法	基线系统	文献[6]	本文方法
医疗	71.7	80.1	82.4	74.3	82.3	83.7	73.0	81.2	83.0
《诛仙》	77.8	86.7	90.3	75.6	88.9	87.7	76.7	87.8	89.0
《斗罗》	81.7	91.9	92.8	81.7	92.1	92.4	81.0	92.0	92.6
发明专利	84.3	85.5	89.8	81.6	86.3	87.2	82.9	85.9	88.5

下载: 导出CSV

| 显示表格

6. 结束语

未登录词和表达鸿沟是目前跨领域中文分词中的难点问题，而目前同时解决两个问题的研究尚不多见。本文针对这两个问题，构建了一个基于新词发现的跨领域中文分词系统，可以自动完成从目标领域语料中提取新词、标注语料和训练网络模型的工作。在此基础上，针对常用的MI+BE新词发现算法提取出的词表垃圾词串多的问题，对互信息和邻接熵的提取进行了改进，提出了一种基于向量增强互信息和加权邻接熵的无监督新词发现算法；针对自动标注语料中存在的噪声文本问题，提出了一种基于对抗式训练的中文分词模型，使用对抗式训练来提取源领域和目标领域的共有特征，以提高中文分词系统的鲁棒性和跨领域表达能力。实验中将使用北大开源新闻语料训练的网络模型提取出的特征迁移到医疗、发明专利和小说领域，结果表明本文所提方法在未登录词率、准确率、召回率和分词F值方面均优于现有模型。

图 1 障碍物建模图

下载: 全尺寸图片幻灯片

图 2 组合算法流程图

下载: 全尺寸图片幻灯片

图 3 针对大型凹形障碍物仿真结果

下载: 全尺寸图片幻灯片

图 4 针对大型凹形障碍物的A*算法的仿真结果

下载: 全尺寸图片幻灯片

图 5 针对大型凹形障碍物的改进人工势场法算法的仿真结果

下载: 全尺寸图片幻灯片

图 6 组合算法在其他场景下的运行结果

下载: 全尺寸图片幻灯片

表 1 人工势场法符号含义

符号	符号含义	符号	符号含义
${\rm{obs}}$	障碍物	${\bf{X}}{\rm{d}}$	目标位置
${U_{{\rm{Xd}}}}(x)$	引力势能	${U_{{\rm{obs}}}}(x)$	斥力势能
${U_{{\rm{art}}}}(x)$	总势能	${{F}}$	合力
${{{F}}_{{\rm{Xd}}}}$	吸引力	${{F}}_{\rm{obs}}$	排斥力
$j$	移动机器人感知到的周边障碍物的个数

下载: 导出CSV

表 2 A*算法符号含义

符号	符号含义	符号	符号含义
$g(\cdot )$	从初始节点到当前移动机器人所在节点node的启发式评估代价	$h(\cdot )$	从当前移动机器人所在节点node到目标节点的启发式评估代价
$(x_{\rm{start}},y_{\rm{start}})$	初始节点坐标	$(x_{\rm{goal}},y_{\rm{goal}})$	目标节点坐标
$(x,y)$	移动机器人实时位置坐标

下载: 导出CSV

表 3 模型描述符号含义

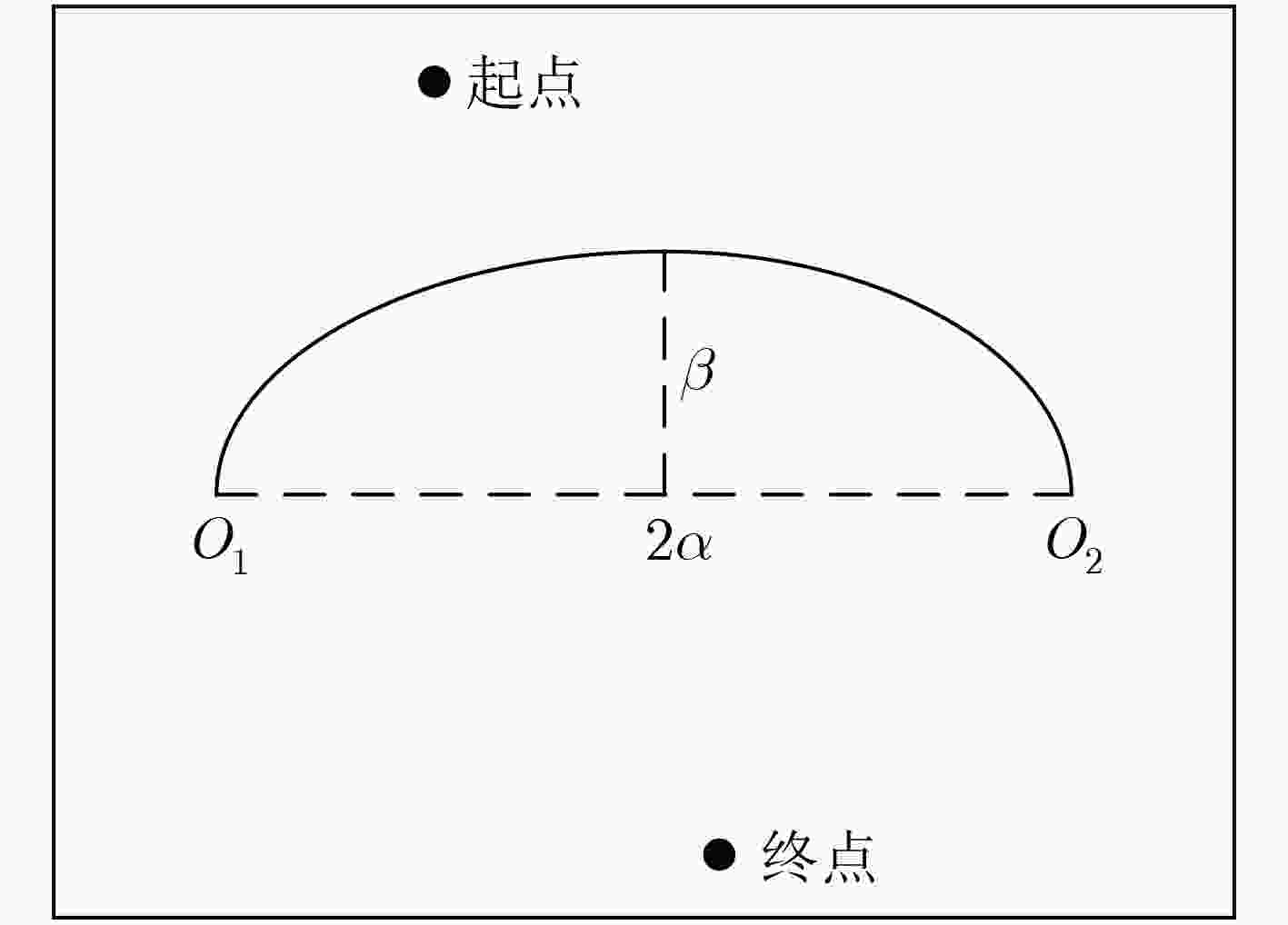
符号	符号含义	符号	符号含义
$O_1$	障碍物的左端点	$O_2$	障碍物的右端点
$2\alpha$	障碍物的长	$\beta$	障碍物的宽
$v_t$	移动机器人的实时线速度	$a$	移动机器人在运行态时的最大速度
$\Delta d$	移动机器人在某段时间内的移动距离	$S_{\rm{obs}}$	所有障碍物总面积
$S_{\rm{map}}$	地图面积	$\rho$	障碍物密度

下载: 导出CSV

表 4 算法性能比较

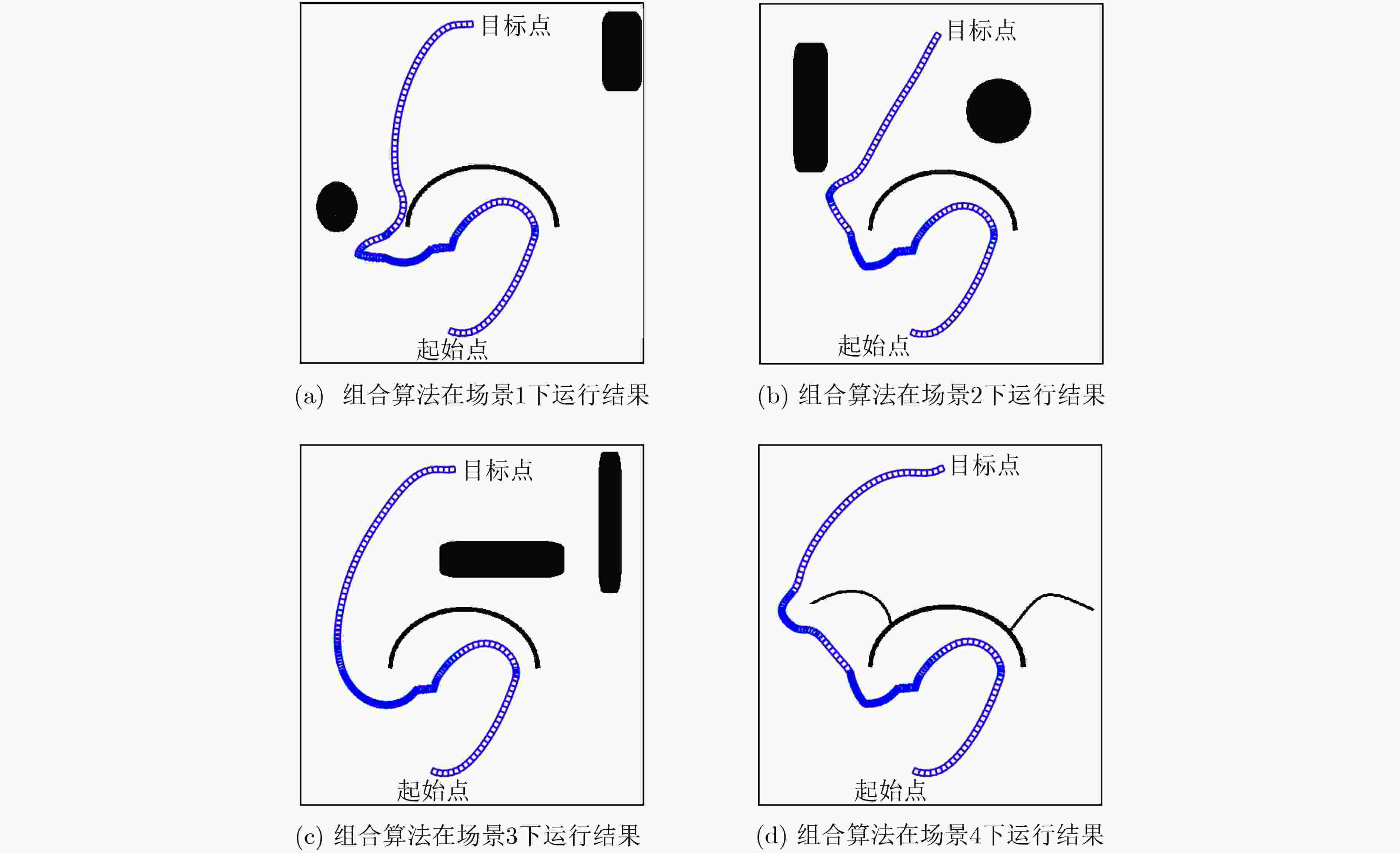
算法	时间(s)	路径长度(m)
A*算法	22.40	1040.69
改进人工势场法^[15]	无穷大	无穷大
本文组合算法	10.62	707.09

下载: 导出CSV

参考文献(15)

王勇臻, 陈燕, 于莹莹. 求解多旅行商问题的改进分组遗传算法[J]. 电子与信息学报, 2017, 39(1): 198–205. doi: 10.11999/JEIT160211

WANG Yongzhen, CHEN Yan, and YU Yingying. Improved grouping genetic algorithm for solving multiple traveling salesman problem[J]. Journal of Electronics &Information Technology, 2017, 39(1): 198–205. doi: 10.11999/JEIT160211

黄长强, 赵克新. 基于改进蚁狮算法的无人机三维航迹规划[J]. 电子与信息学报, 2018, 40(7): 1532–1538. doi: 10.11999/JEIT170961

HUANG Changqiang and ZHAO Kexin. Three dimensional path planning of UAV with improved ant lion optimizer[J]. Journal of Electronics &Information Technology, 2018, 40(7): 1532–1538. doi: 10.11999/JEIT170961

KHATIB O. Real-time obstacle avoidance for manipulators and mobile robots[J]. The International Journal of Robotics Research, 1986, 5(1): 90–98. doi: 10.1177/027836498600500106

PARK M G, JEON J H, and LEE M C. Obstacle avoidance for mobile robots using artificial potential field approach with simulated annealing[C]. 2001 IEEE International Symposium on Industrial Electronics, Pusan, South Korea, 2001: 1530–1535. doi: 10.1109/ISIE.2001.931933.

况菲, 王耀南. 基于混合人工势场-遗传算法的移动机器人路径规划仿真研究[J]. 系统仿真学报, 2006, 18(3): 774–777. doi: 10.16182/j.cnki.joss.2006.03.061

KUANG Fei and WANG Yaonan. Robot path planning based on hybrid artificial potential field/genetic algorithm[J]. Journal of System Simulation, 2006, 18(3): 774–777. doi: 10.16182/j.cnki.joss.2006.03.061

LEE D, JEONG J, KIM Y H, et al. An improved artificial potential field method with a new point of attractive force for a mobile robot[C]. The 2nd International Conference on Robotics and Automation Engineering, Shanghai, China, 2017: 63–67. doi: 10.1109/ICRAE.2017.8291354.

ROSTAMI S M H, SANGAIAH A K, WANG Jin, et al. Obstacle avoidance of mobile robots using modified artificial potential field algorithm[J]. EURASIP Journal on Wireless Communications and Networking, 2019(1): No. 70, 1–19. doi: 10.1186/s13638-019-1396-2

HART P E, NILSSON N J, and RAPHAEL B. A formal basis for the heuristic determination of minimum cost paths[J]. IEEE Transactions on Systems Science and Cybernetics, 1968, 4(2): 100–107. doi: 10.1109/TSSC.1968.300136

DECHTER R and PEARL J. Generalized best-first search strategies and the optimality of A*[J]. Journal of the ACM, 1985, 32(3): 505–536. doi: 10.1145/3828.3830

田景文, 孔垂超, 高美娟. 一种车辆路径规划的改进混合算法[J]. 计算机工程与应用, 2014, 50(14): 58–63. doi: 10.3778/j.issn.1002-8331.1208-0319

TIAN Jingwen, KONG Chuichao, and GAO Meijuan. Improved hybrid algorithm of vehicle path planning[J]. Computer Engineering and Applications, 2014, 50(14): 58–63. doi: 10.3778/j.issn.1002-8331.1208-0319

胡中华, 潘洲, 王凯凯. 基于混合算法的动态路径规划[J]. 煤矿机械, 2015, 36(12): 243–245. doi: 10.13436/j.mkjx.201512103

HU Zhonghua, PAN Zhou, and WANG Kaikai. Dynamic path planning based on hybrid algorithm[J]. Coal Mine Machinery, 2015, 36(12): 243–245. doi: 10.13436/j.mkjx.201512103

唐志荣, 冀杰, 吴明阳, 等. 基于改进人工势场法的车辆路径规划与跟踪[J]. 西南大学学报: 自然科学版, 2018, 40(6): 174–182. doi: 10.13718/j.cnki.xdzk.2018.06.025

TANG Zhirong, JI Jie, WU Mingyang, et al. Vehicles path planning and tracking based on an improved artificial potential field method[J]. Journal of Southwest University:Natural Science Edition, 2018, 40(6): 174–182. doi: 10.13718/j.cnki.xdzk.2018.06.025

赵奇, 赵阿群. 一种基于A*算法的多径寻由算法[J]. 电子与信息学报, 2013, 35(4): 952–957. doi: 10.3724/SP.J.1146.2012.00983

ZHAO Qi and ZHAO Aqun. A multi-path routing algorithm base on A* algorithm[J]. Journal of Electronics &Information Technology, 2013, 35(4): 952–957. doi: 10.3724/SP.J.1146.2012.00983

DIJKSTRA E W. A note on two problems in connexion with graphs[J]. Numerische Mathematik, 1959, 1(1): 269–271. doi: 10.1007/BF01386390

沈文君. 基于改进人工势场法的机器人路径规划算法研究[D]. [硕士论文], 暨南大学, 2009.

SHEN Wenjun. Algorithm research of path planning for robot based on improved artifical potential field[D]. [Master dissertation], Jinan University, 2009.

施引文献

期刊类型引用(6)

1.	付尧明，陈余杰，侯宽新，蒋正. 通航飞机维修文本故障数据的分词方法研究. 计算机仿真. 2025(01): 30-35+125 . 百度学术
2.	徐晓涛. 大数据客户热词分析系统的架构设计. 武夷学院学报. 2024(09): 26-31 . 百度学术
3.	夏清洁，攸彩红，赵英杰. 改进向量空间模型的相似专利检测技术研究. 粘接. 2024(11): 193-196 . 百度学术
4.	乔凯庆，汪海瑛，王婧，卢剑，杨志鹏，王小兵. 基于6C系统大数据分析的接触网零部件缺陷特征研究. 中国铁路. 2023(07): 39-44 . 百度学术
5.	樊继慧，滕少华. 基于局部敏感哈希的K邻近算法识别垃圾短信. 济南大学学报(自然科学版). 2023(06): 746-751 . 百度学术
6.	夏飞，陈帅琦，华珉，蒋碧鸿. 基于改进BERT的电力领域中文分词方法. 计算机应用. 2023(12): 3711-3718 . 百度学术

其他类型引用(8)

资源附件(0)

访问统计

图(6) / 表(4)

计量

文章访问数: 2614
HTML全文浏览量: 1298
PDF下载量: 86
被引次数: 14

1. 引言
2. 基线系统
3. 基于向量增强互信息和加权邻接熵的无监督新词发现算法
3.1 向量增强互信息
3.2 加权邻接熵
3.3 候选词筛选
4. 基于对抗式训练的中文分词模型
5. 实验结果及分析
5.1 实验设置
5.2 新词发现
5.3 基于对抗式训练的分词算法
5.4 与现有方法的对比
6. 结束语

1. 引言
2. 基线系统
3. 基于向量增强互信息和加权邻接熵的无监督新词发现算法
3.1 向量增强互信息
3.2 加权邻接熵
3.3 候选词筛选
4. 基于对抗式训练的中文分词模型
5. 实验结果及分析
5.1 实验设置
5.2 新词发现
5.3 基于对抗式训练的分词算法
5.4 与现有方法的对比
6. 结束语

参考文献(15)

施引文献

资源附件(0)

访问统计

姓名
邮箱
手机号码
标题
留言内容
验证码

留言板

一种针对大型凹型障碍物的组合导航算法

doi: 10.11999/JEIT190179

通讯作者:
冯超　cfeng@qlu.edu.cn

计量

Integrated Navigation Algorithm for Large Concave Obstacles

1. 引言

2. 基线系统

3. 基于向量增强互信息和加权邻接熵的无监督新词发现算法

3.1 向量增强互信息

3.2 加权邻接熵

3.3 候选词筛选

4. 基于对抗式训练的中文分词模型

5. 实验结果及分析

5.1 实验设置

5.2 新词发现

5.3 基于对抗式训练的分词算法

5.4 与现有方法的对比

6. 结束语

期刊类型引用(6)

其他类型引用(8)

计量

目录

1. 引言

2. 基线系统

3. 基于向量增强互信息和加权邻接熵的无监督新词发现算法

3.1 向量增强互信息

3.2 加权邻接熵

3.3 候选词筛选

4. 基于对抗式训练的中文分词模型

5. 实验结果及分析

5.1 实验设置

5.2 新词发现

5.3 基于对抗式训练的分词算法

5.4 与现有方法的对比

6. 结束语

留言板

一种针对大型凹型障碍物的组合导航算法

doi: 10.11999/JEIT190179

通讯作者: 冯超 cfeng@qlu.edu.cn

计量

出版历程

Integrated Navigation Algorithm for Large Concave Obstacles

1. 引言

2. 基线系统

3. 基于向量增强互信息和加权邻接熵的无监督新词发现算法

3.1 向量增强互信息

3.2 加权邻接熵

3.3 候选词筛选

4. 基于对抗式训练的中文分词模型

5. 实验结果及分析

5.1 实验设置

5.2 新词发现

5.3 基于对抗式训练的分词算法

5.4 与现有方法的对比

6. 结束语

期刊类型引用(6)

其他类型引用(8)

计量

出版历程

目录

1. 引言

2. 基线系统

3. 基于向量增强互信息和加权邻接熵的无监督新词发现算法

3.1 向量增强互信息

3.2 加权邻接熵

3.3 候选词筛选

4. 基于对抗式训练的中文分词模型

5. 实验结果及分析

5.1 实验设置

5.2 新词发现

5.3 基于对抗式训练的分词算法

5.4 与现有方法的对比

6. 结束语

通讯作者:
冯超　cfeng@qlu.edu.cn