Robust and Efficient Sparse-feature Enhancementfor Generalized SAR Imagery
-
摘要: 针对合成孔径雷达(SAR)成像中的稀疏特征增强问题,传统方法难以在精度与效率之间实现有效的平衡。该文提出基于复数交替方向多乘子方法(C-ADMM),针对SAR稀疏特征增强建立增广的拉格朗日优化方程,并引入复数
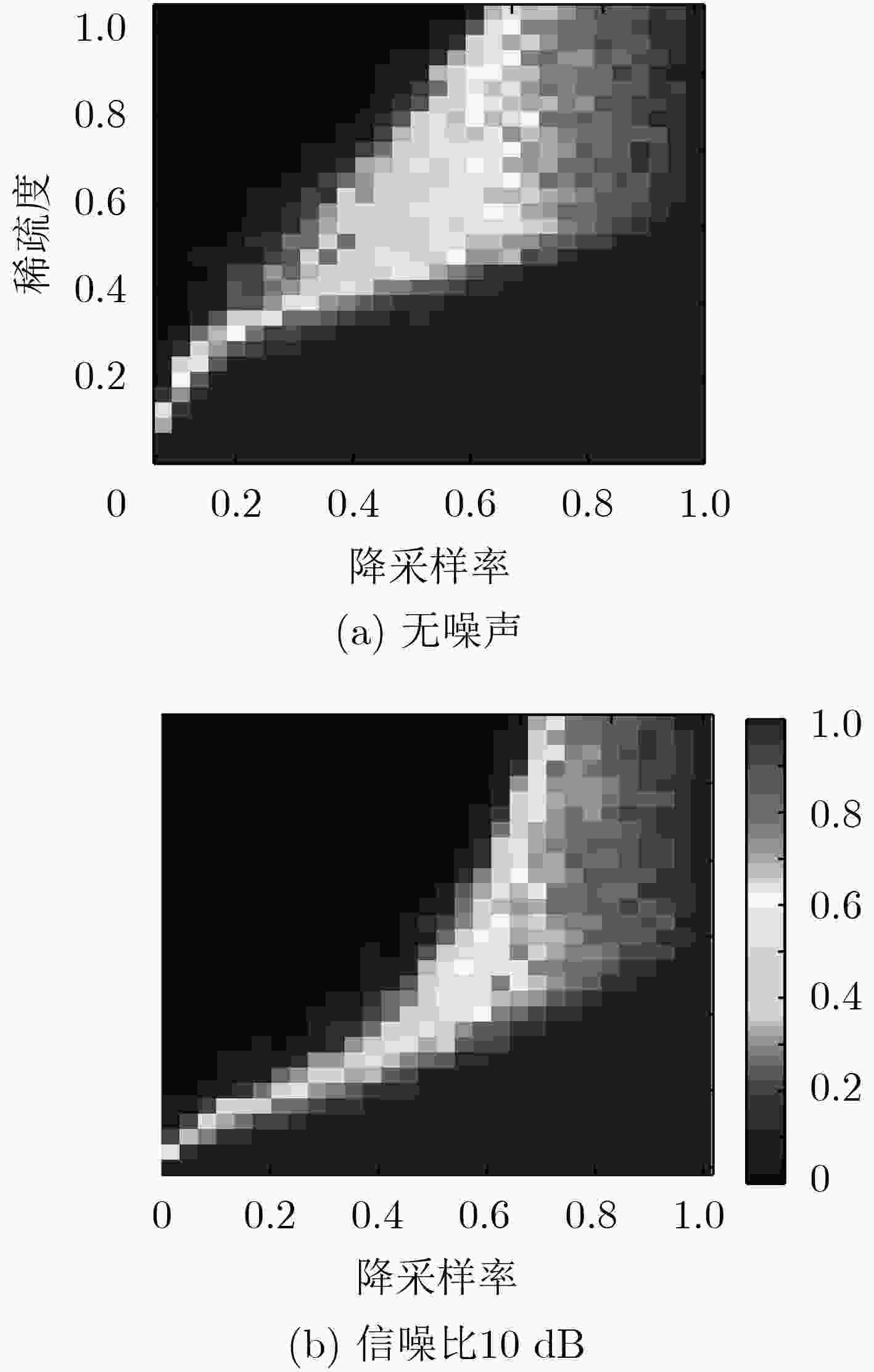
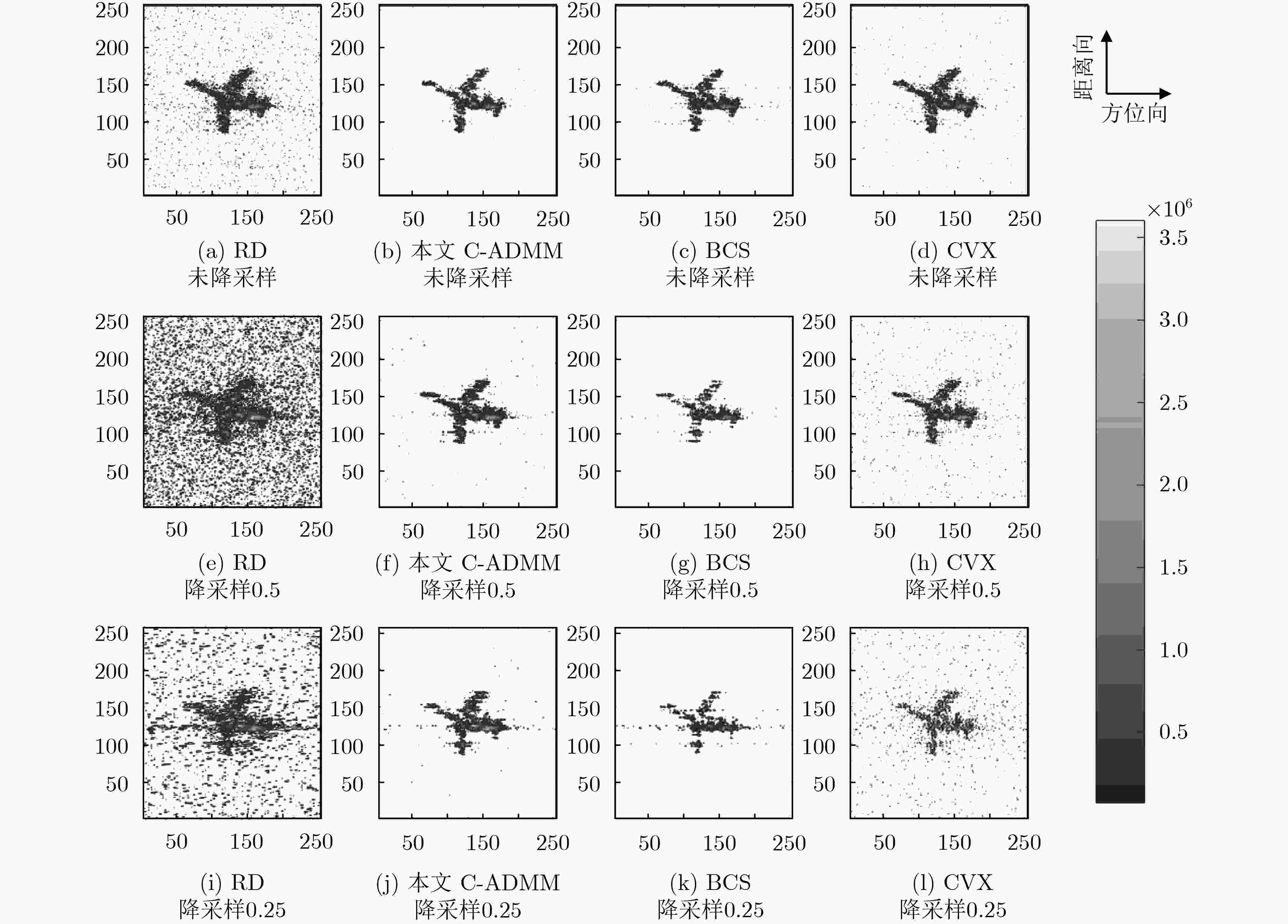
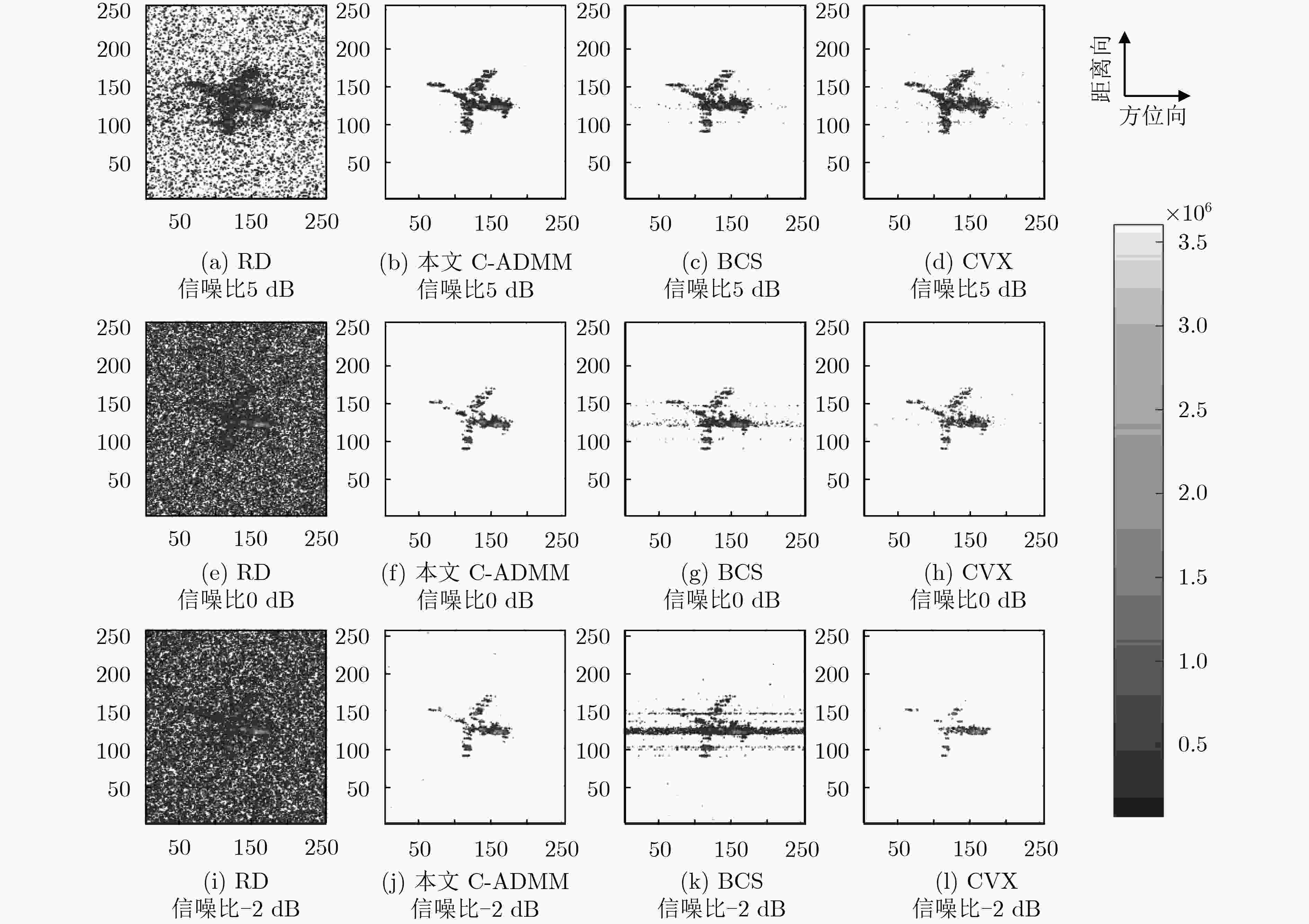
${\ell _1}$ 范数邻近算子,基于高斯-赛德尔思想进行对偶迭代运算,从而在复数回波数据域内对多种SAR模式的实测数据进行成像。实验部分首先通过仿真数据的相变图(PTD)验证C-ADMM算法对于复数数据的稀疏恢复性能,然后选取地面静止场景和地面运动目标的原始SAR图像和逆SAR图像实测数据,与凸优化(CVX)方法和贝叶斯压缩感知(BCS)方法进行对比试验,最后验证了该文所提算法在稀疏特征增强应用中的稳健性、高效性和通用性。-
关键词:
- 合成孔径雷达 /
- 稀疏特征增强 /
- 复数交替方向多乘子方法 /
- 增广拉格朗日优化方程
Abstract: For the problem of sparse feature enhancement in Synthetic Aperture Radar (SAR) imagery, conventional methods are difficult to achieve a preferable balance between accuracy and efficiency. In this paper, a robust and efficient SAR imaging algorithm based on Complex Alternating Direction Method of Multipliers(C-ADMM) is proposed for general SAR imaging feature enhancement within complex raw data domain. The problem is firstly imposed by an augmented Lagrange function, and the complex${\ell _1}$ -norm of the intended SAR image is jointly formulated within the C-ADMM framework. Then, the proximal mapping of the sparse feature is derived as a soft-thresholding operator. Further, an iterative processing procedure is designed according to Gaussian-Deidel principle, and the convergence of the proposed algorithm is analyzed. In the experiment, the performance of the proposed algorithm is firstly examined by the simulated data in terms of Phase Transition Diagram (PTD) under different under-sampling rate and degree of sparsity. Then, various raw SAR and Inverse SAR(ISAR) data, for both stationary ground scene and Ground Moving Target Imaging(CMTIm), are applied to further verifying the proposed C-ADMM, and comparisons with classical Convex(CVX) and Bayesian Compress Sensing(BCS) algorithms are performed, so that both the effectiveness and superiority of the C-ADMM algorithm can be verified. -
表 1 C-ADMM稀疏特征增强算法流程
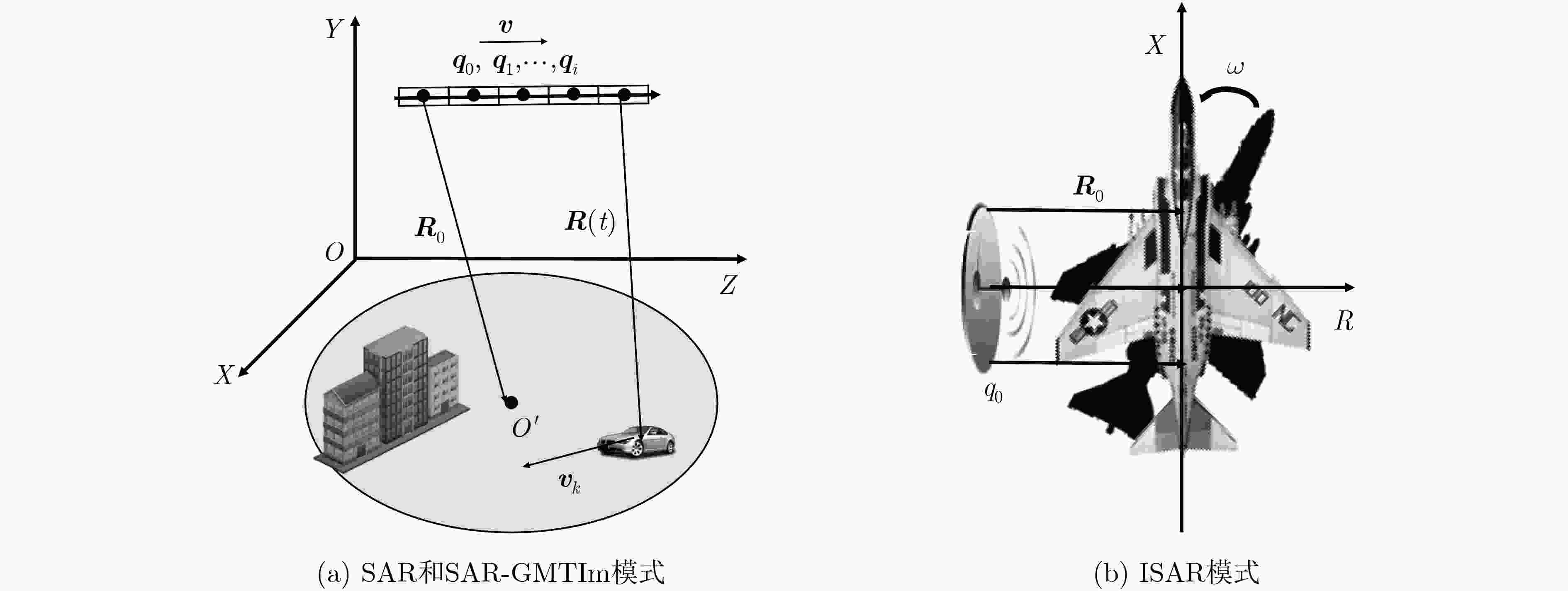
(1) 初始化,输入SAR原始数据; (2) 信号预处理,得到通用信号模型$S\left( {\hat r,t} \right)$或$S\left( {\hat r,{t'}} \right)$; (3) 设定初值${{X}^0} = {{Z}^0} = {{U}^0} = 0$,构造字典${A}$=${{A}_0}$或${A}\left( {{\gamma _d}} \right)$; (4) 设定迭代次数与目标精度,若停止准则不满足,进行循环; (5) 更新目标图像
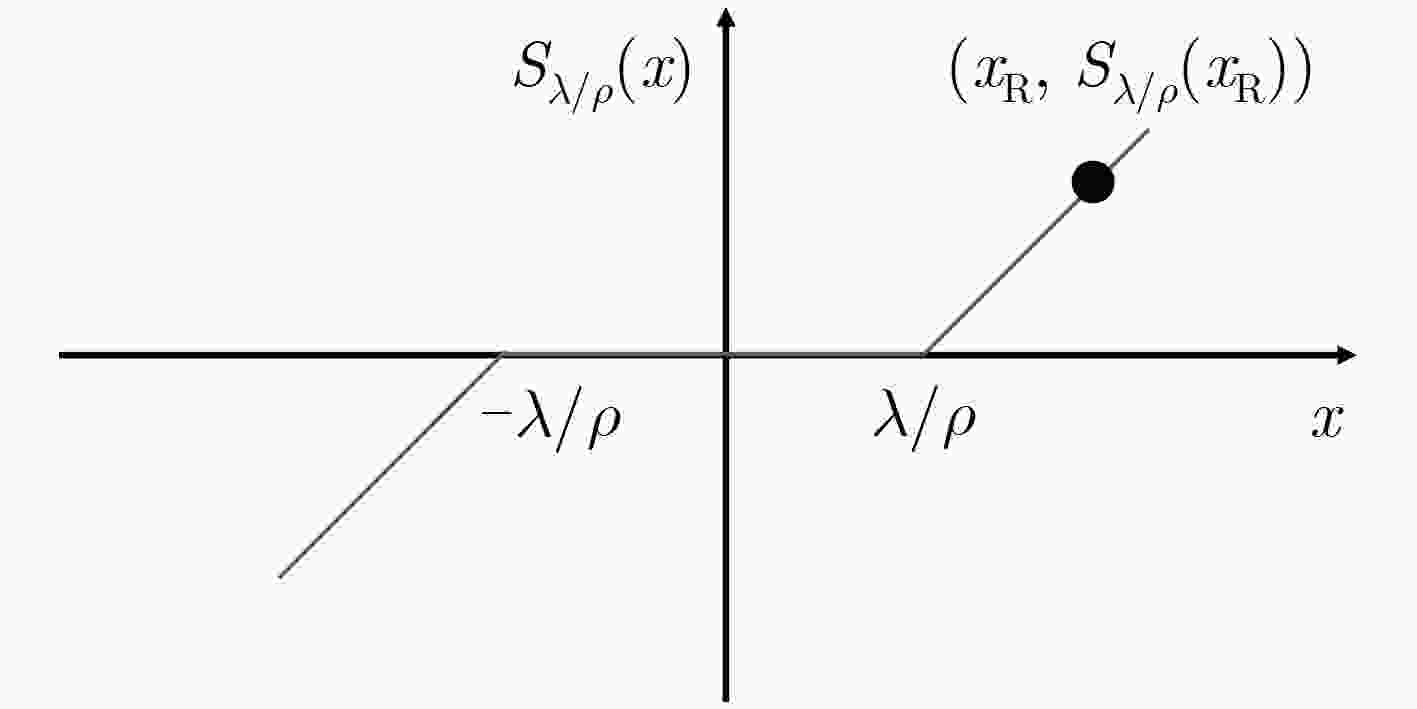
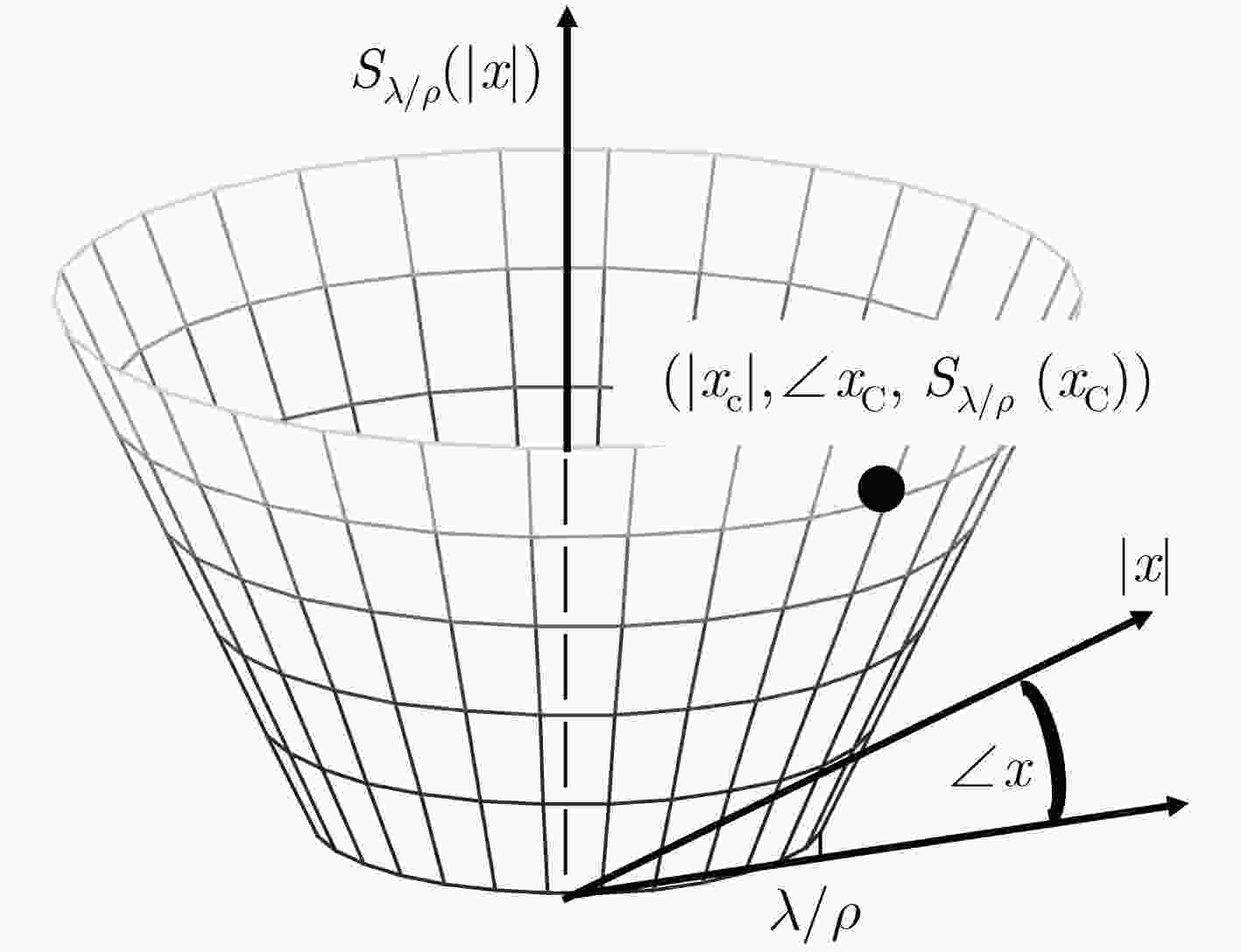
${{X}^{k + 1}} = {\left( {{{A}^{\rm{H}}}{A} + \rho {I}} \right)^{ - 1}}\left\{ {{{A}^{\rm{H}}}{Y} + \rho \left( {{{Z}^k} - {{U}^k}} \right)} \right\}$;(6) 更新软阈值${{Z}^{k + 1}} = {S_{\lambda /\rho }}\left( {{{X}^{k + 1}} + {{U}^k}} \right)$; (7) 更新对偶变量${{U}^{k + 1}} = {{U}^k} + {{X}^{k + 1}} - {{Z}^{k + 1}}$; (8) 若不满足停止准则,继续步骤5—步骤7,若满足停止准则,跳 出循环; (9) 输出稀疏特征增强后的图像。 -
DONOHO D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289–1306. doi: 10.1109/TIT.2006.871582 CANDES E J, ROMBERG J, and TAO T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information[J]. IEEE Transactions on Information Theory, 2006, 52(2): 489–509. doi: 10.1109/TIT.2005.862083 BARANIUK R G. Compressive sensing [Lecture Notes][J]. IEEE Signal Processing Magazine, 2007, 24(4): 118–121. doi: 10.1109/MSP.2007.4286571 TELLO M T, LOPEZ-DEKKER P, AND MALLORQUI J J. A novel strategy for radar imaging based on compressive sensing[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(22): 4285–4295. doi: 10.1109/TGRS.2010.2051231 ÖNHON N Ö and CETIN M. A sparsity-driven approach for joint SAR imaging and phase error correction[J]. IEEE Transactions on Image Processing, 2012, 21(4): 2075–2088. doi: 10.1109/TIP.2011.2179056 YANG Lei, ZHAO Lifan, ZHOU Song, et al. Sparsity-driven SAR imaging for highly maneuvering ground target by the combination of time-frequency analysis and parametric Bayesian learning[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2017, 10(4): 1443–1455. doi: 10.1109/JSTARS.2016.2611005 YANG Lei, ZHAO Lifan, BI Guoan, et al. SAR ground moving target imaging algorithm based on parametric and dynamic sparse Bayesian learning[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(4): 2254–2267. doi: 10.1109/TGRS.2015.2498158 ZHAO Lifan, WANG Lu, BI Guoan, et al. An autofocus technique for high-resolution inverse synthetic aperture radar imagery[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(10): 6392–6403. doi: 10.1109/TGRS.2013.2296497 TROPP J A and GILBERT A C. Signal recovery from random measurements via orthogonal matching pursuit[J]. IEEE Transactions on Information Theory, 2007, 53(12): 4655–4666. doi: 10.1109/TIT.2007.909108 MUTHUKRISHNAN S. Data streams: Algorithms and applications[J]. Foundations and Trends ® in Theoretical Computer Science, 2005, 1(2): 117–236. doi: 10.1561/0400000002 BOYD S, PARIKH N, CHU E, et al. Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers[J]. Foundations and Trends® in Machine Learning, 2011, 3(1): 1–122. doi: 10.1561/2200000016. MALEKI A, ANITORI L, YANG Zai, et al. Asymptotic analysis of complex LASSO via complex approximate message passing (CAMP)[J]. IEEE Transactions on Information Theory, 2013, 59(7): 4290–4308. doi: 10.1109/TIT.2013.2252232 侯丽丽, 郑明洁, 宋红军, 等. 多通道高分辨率宽测绘带SAR系统杂波抑制技术研究[J]. 电子与信息学报, 2016, 38(3): 635–642. doi: 10.11999/JEIT150659HOU Lili, ZHENG Mingjie, SONG Hongjun, et al. Research on clutter suppression for multichannel high-resolution wide-swath SAR System[J]. Journal of Electronics &Information Technology, 2016, 38(3): 635–642. doi: 10.11999/JEIT150659 王力宝, 许稼, 向家彬, 等. 基于DPCA和多分辨分析的SAR微弱运动目标检测[J]. 电子与信息学报, 2007, 29(12): 2843–2847. doi: 10.3724/SP.J.1146.2006.00710WANG Libao, XU Jia, XIANG Jiabin, et al. SAR weak moving target detection based on DPCA and multi-resolution analysis[J]. Journal of Electronics &Information Technology, 2007, 29(12): 2843–2847. doi: 10.3724/SP.J.1146.2006.00710 金艳, 段鹏婷, 姬红兵. 复杂噪声环境下基于LVD的LFM信号参数估计[J]. 电子与信息学报, 2014, 36(5): 1106–1112. doi: 10.3724/SP.J.1146.2013.01013JIN Yan, DUAN Pengting, and JI Hongbing. Parameter estimation of LFM signals based on LVD in complicated noise environments[J]. Journal of Electronics &Information Technology, 2014, 36(5): 1106–1112. doi: 10.3724/SP.J.1146.2013.01013 保铮, 邢孟道, 王彤. 雷达成像技术[M]. 北京: 电子工业出版社, 2005.BAO Zheng, XING Mengdao, and WANG Tong. Radar Imaging Technology[M]. Beijing: Electronic Industry Press, 2005. TIBSHIRANI R. Regression shrinkage and selection via the LASSO: A retrospective[J]. Journal of the Royal Statistical Society: Series B (Statistical Methodology) , 2011, 73(3): 273–282. doi: 10.1111/J.1467-9868.2011.00771.X DONOHO D L and TANNER J. Precise undersampling theorems[J]. Proceedings of the IEEE, 2010, 98(6): 913–924. doi: 10.1109/JPROC.2010.2045630 张增辉, 郁文贤. 稀疏微波SAR图像特征分析与目标检测研究[J]. 雷达学报, 2016, 5(1): 42–56. doi: 10.12000/JR15097ZHANG Zenghui and YU Wenxian. Feature understanding and target detection for sparse microwave synthetic aperture radar images[J]. Journal of Radars, 2016, 5(1): 42–56. doi: 10.12000/JR15097 刘向阳, 杨君刚, 孟进, 等. 低信噪比下基于Hough变换的前视阵列SAR稀疏三维成像[J]. 雷达学报, 2017, 6(3): 316–323. doi: 10.12000/JR17011LIU Xiangyang, YANG Jungang, MENG Jin, et al. Sparse three-dimensional imaging based on Hough transform for forward-looking array SAR in Low SNR[J]. Journal of Radars, 2017, 6(3): 316–323. doi: 10.12000/JR17011 -







 下载:
下载:





 下载:
下载:
