Multi-party Contract Signing Protocol Based on Certificateless
-
摘要: 线上合同签署在电子商务中日益普及，在互不信任的签署方之间签署一份合同并不是一件简单的事情，各方就合同签署问题提出过许多合同签署协议。其中较多的协议是带有第三方参与的，但是在效率方面并不占优势，且易出现安全问题。现有借助区块链技术取代第三方参与的合同签署协议中，区块链的公开验证对不管是签署方还是待签署合同的敏感信息又发起了挑战。且大多协议针对于双方合同签署，随着签署方数量的增加，协议的通信成本和复杂度都在急剧增加。该文结合现有协议，提出一个高效的多方合同签署协议，协议中通过基于无证书的高效聚合签名方案，用于提高区块链下签署方签名验证效率，在区块链上仅公开签署方的临时密钥以减少系统开销。该协议满足正确性、安全性、公平性、私密性以及高效性。Abstract: Online contract signing is becoming more and more popular in e-commerce. It is not easy to sign a contract between two parties who do not trust each other. Many of these protocols involve the participation of third parties, but they are not advantageous in efficiency and prone to security problems. Currently, contract signing agreements with third-party participation are replaced by block chain technology, but the public verification of block chain challenges the sensitive information of both the signer and the contract to be signed. And most of the agreements are for the signing of contracts between the two parties. With the increase of the number of signatories, the communication cost and complexity of the agreements increase sharply. Combined with the existing protocols, this paper proposes an efficient multi-party contract signing protocol. In the protocol, an efficient aggregation signature scheme based on no certificate is used to improve the signature verification efficiency of the signer under the block chain, and only the temporary key of the signer is disclosed on the block chain to reduce the system overhead. The protocol satisfies the requirements of correctness, security, fairness, privacy and high efficiency.
-
Key words:
- Aggregation verifiable signature /
- Privacy protection /
- Blockchain /
- Contract signing
-
BLUM M. How to exchange (secret) keys[C]. The Fifteenth Annual ACM Symposium on Theory of Computing, Boston, USA, 1983: 440–447. Al-RIYAMI S S and PATERSON K G. Certificateless public key cryptography[C]. The 9th International Conference on the Theory and Application of Cryptology and Information Security, Taipei, China, 2003: 452–473. BONEH D, GENTRY C, LYNN B, et al. Aggregate and verifiably encrypted signatures from bilinear maps[C]. 2003 International Conference on the Theory and Applications of Cryptographic Techniques, Warsaw, Poland, 2003: 416–432. 周彦伟, 杨波, 张文政. 高效可证安全的无证书聚合签名方案[J]. 软件学报, 2015, 26(12): 3204–3214. doi: 10.13328/j.cnki.jos.004830ZHOU Yanwei, YANG Bo, and ZHANG Wenzheng. Efficient and provide security certificateless aggregate signature scheme[J]. Journal of Software, 2015, 26(12): 3204–3214. doi: 10.13328/j.cnki.jos.004830 曹素珍, 郎晓丽, 刘祥震, 等. 可证安全的高效无证书聚合签名方案[J]. 信息网络安全, 2019, 19(1): 42–50. doi: 10.3969/j.issn.1671-1122.2019.01.006CAO Suzhen, LANG Xiaoli, LIU Xiangzhen, et al. Probably secure and efficient certificateless aggregate signature scheme[J]. Netinfo Security, 2019, 19(1): 42–50. doi: 10.3969/j.issn.1671-1122.2019.01.006 许芷岩, 吴黎兵, 李莉, 等. 新的无证书广义指定验证者聚合签名方案[J]. 通信学报, 2017, 38(11): 2017220.XU Zhiyan, WU Libing, LI Li, et al. New certificateless aggregate signature scheme with universal designated verifier[J]. Journal on Communications, 2017, 38(11): 2017220. 苏靖枫, 柳菊霞. 不含双线性对的高效无证书聚合签密方案[J]. 计算机应用, 2018, 38(2): 374–378. doi: 10.11772/j.issn.1001-9081.2017081984SU Jingfeng and LIU Juxia. Efficient certificateless aggregate signcryption scheme without bilinear pairings[J]. Journal of Computer Applications, 2018, 38(2): 374–378. doi: 10.11772/j.issn.1001-9081.2017081984 WAN Zhiguo, DENG R H, and LEE D. Electronic contract signing without using trusted third party[C]. Proceedings of the 9th International Conference on Network and System Security, New York, USA, 2015: 386–394. 田海博, 何杰杰, 付利青. 基于公开区块链的隐私保护公平合同签署协议[J]. 密码学报, 2017, 4(2): 187–198.TIAN Haibo, HE Jiejie, and FU Liqing. A privacy preserving fair contract signing protocol based on block chains[J]. Journal of Cryptologic Research, 2017, 4(2): 187–198. 吴进喜, 高莹, 张宗洋, 等. 基于区块链的多方隐私保护公平合同签署协议[J]. 信息安全学报, 2018, 3(3): 8–16.WU Jinxi, GAO Ying, ZHANG Zongyang, et al. A multi-party privacy preserving fair contract signing protocol based on blockchains[J]. Journal of Cyber Security, 2018, 3(3): 8–16. HUANG Hui, LI K C, and CHEN Xiaofeng. A fair three-party contract singing protocol based on blockchain[C]. The 9th International Symposium on Cyberspace Safety and Security, Xi’an, China, 2017: 72–85. 高莹, 吴进喜. 基于区块链的高效公平多方合同签署协议[J]. 密码学报, 2018, 5(5): 556–567.GAO Ying and WU Jinxi. Efficient multi-party fair contract signing protocol based on blockchains[J]. Journal of Cryptologic Research, 2018, 5(5): 556–567. 周彦伟, 杨波, 王青龙. 安全的无双线性映射的无证书签密机制[J]. 软件学报, 2017, 28(10): 2757–2768. doi: 10.13328/j.cnki.jos.005150ZHOU Yanwei, YANG Bo, and WANG Qinglong. Secure certificateless signcryption scheme without bilinear pairing[J]. Journal of Software, 2017, 28(10): 2757–2768. doi: 10.13328/j.cnki.jos.005150 韦性佳, 张京花, 刘增芳, 等. 具有前向安全性质的基于身份的聚合签名方案[J]. 计算机科学, 2018, 45(6A): 387–391.WEI Xingjia, ZHANG Jinghua, LIU Zengfang, et al. Identity based aggregate signature scheme with forward security[J]. Computer Science, 2018, 45(6A): 387–391. 王亚飞, 张睿哲. 强安全无对的无证书签名方案[J]. 通信学报, 2013, 34(2): 94–99. doi: 10.3969/j.issn.1000-436x.2013.02.011WANG Yafei and ZHANG Ruizhe. Strongly secure certificateless signature scheme without pairings[J]. Journal on Communications, 2013, 34(2): 94–99. doi: 10.3969/j.issn.1000-436x.2013.02.011 -
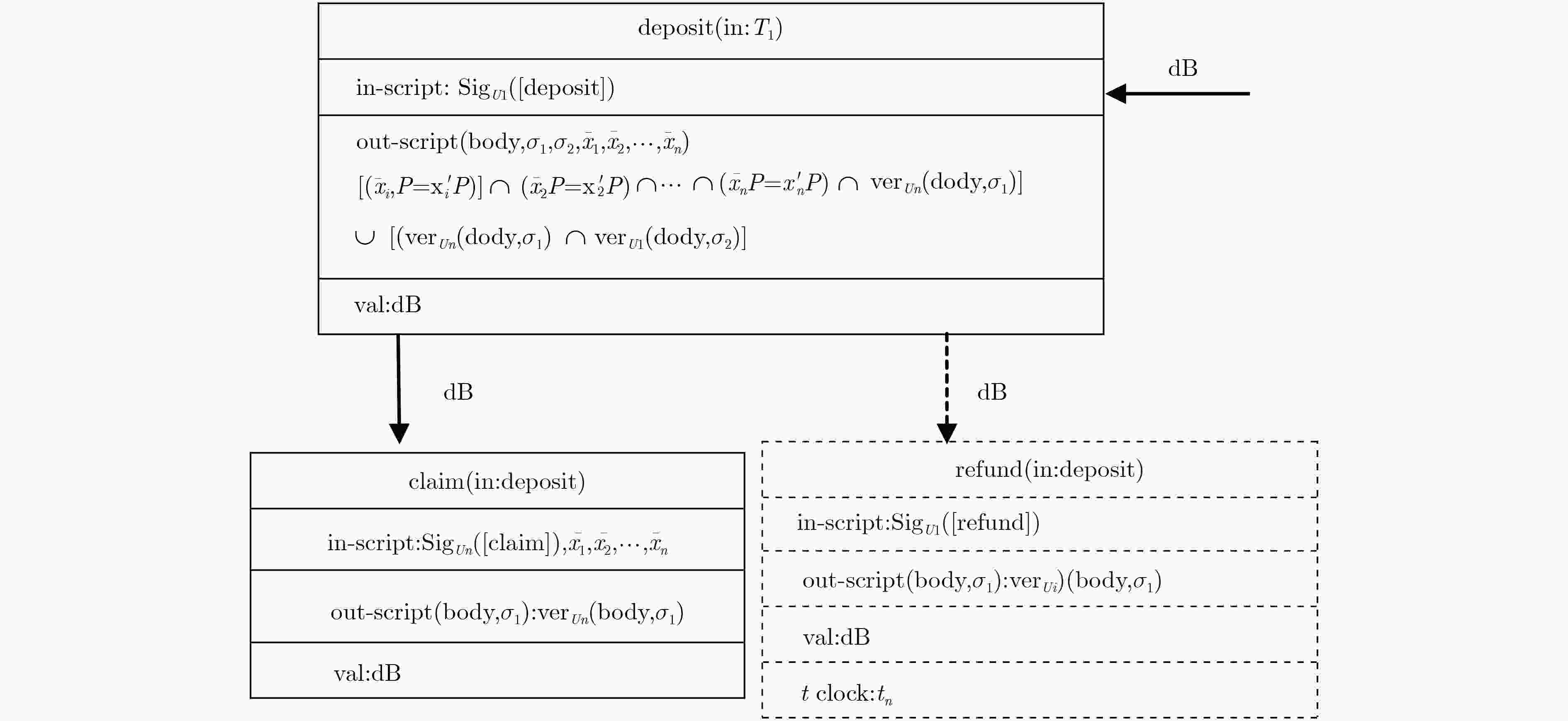
下载:
图(2) / 表(1)
计量
- 文章访问数: 2863
- HTML全文浏览量: 1433
- PDF下载量: 109
- 被引次数: 0
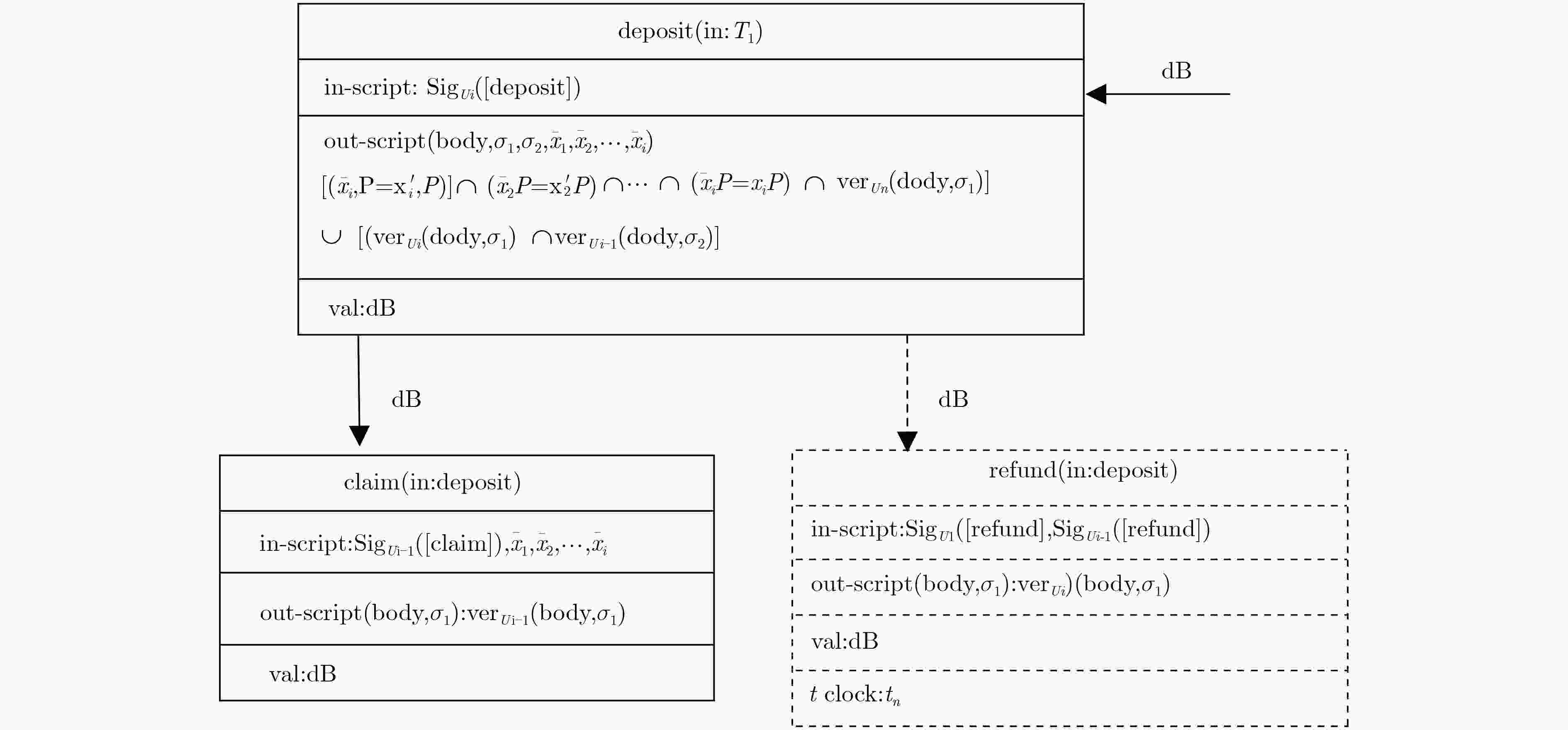
下载:
