Iterative Multiple Signal Classification Algorithm with Small Sample Size
-
摘要:
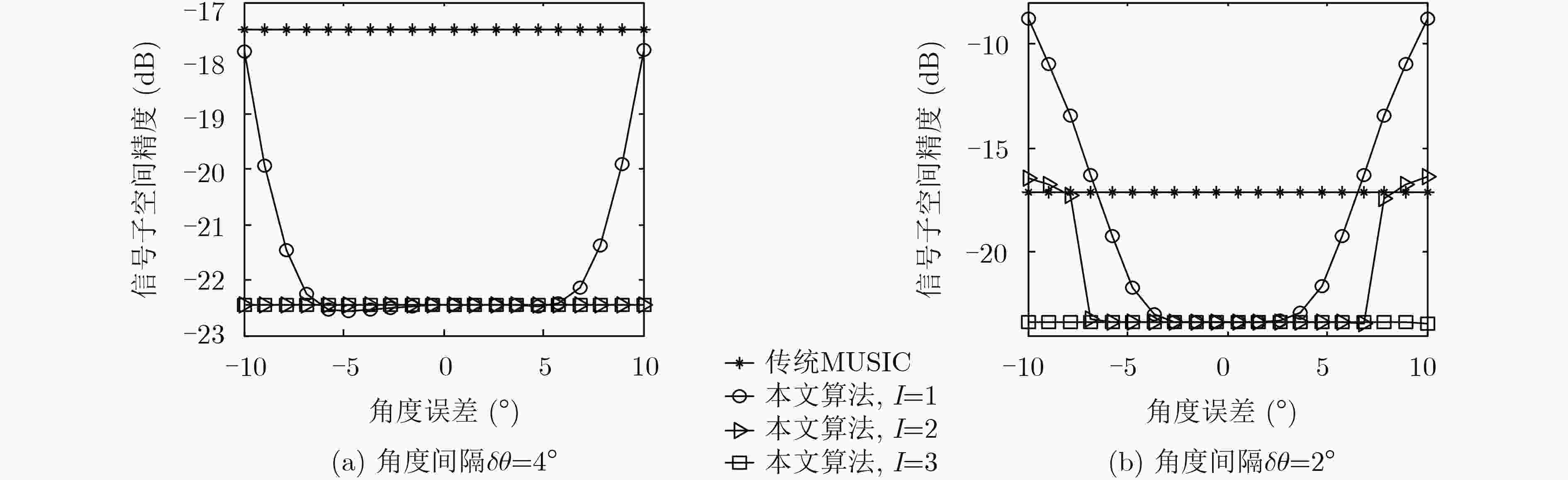
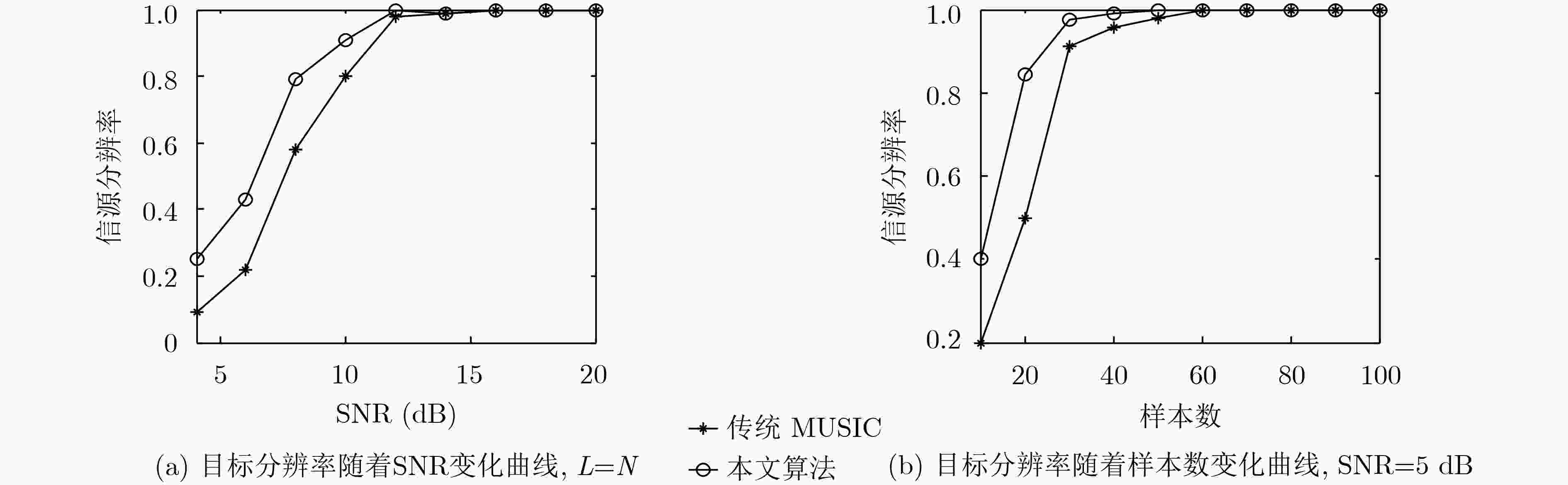
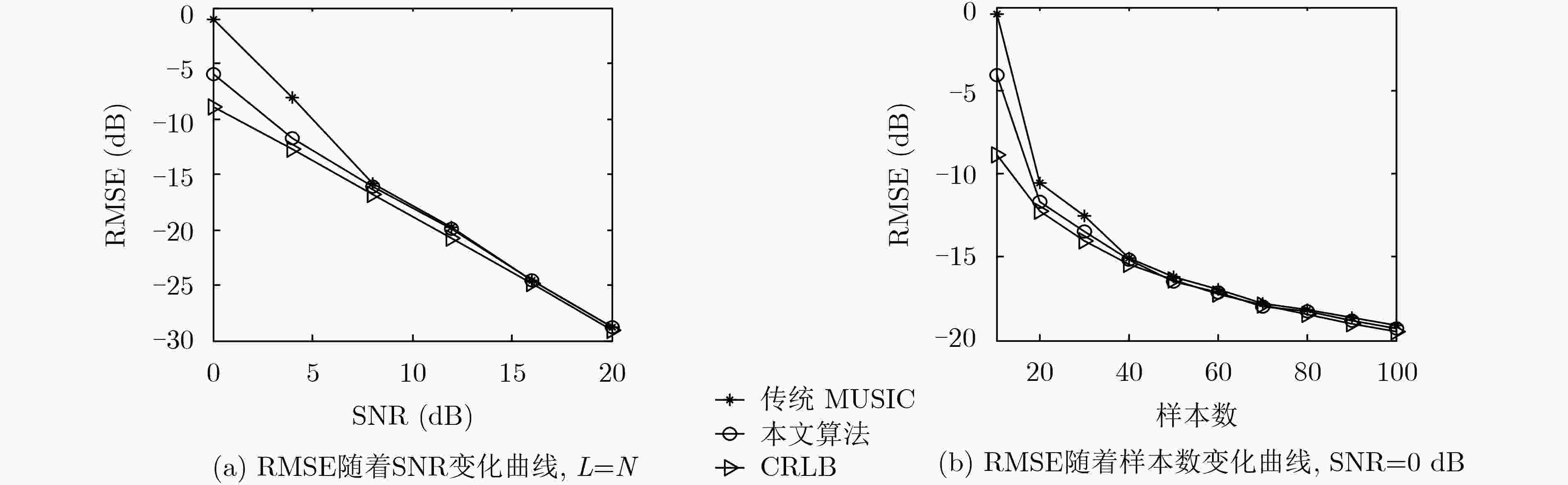
当样本数不足时,由采样协方差矩阵特征分解得到的噪声子空间偏离其真实值,使得多重信号分类(MUSIC)算法目标角度(DOA)估计性能下降。为了解决这个问题,该文提出了一种迭代算法通过校正信号子空间来提高MUSIC算法性能。该方法首先利用采样协方差矩阵特征分解得到的噪声子空间粗略估计目标角度;其次基于信源的稀疏性和导向矢量的低秩特性,由上一步得到的目标角度以及其邻域角度对应的导向矢量构造一个新的信号子空间;最后通过解一个优化问题来校正信号子空间。仿真结果表明,该算法有效地提高了子空间估计精度。基于新的信号子空间实现MUSIC DOA估计可以使得性能得到改善,且在低样本数下改善尤为明显。
Abstract:For cases with small samples, the estimated noise subspace obtained from sample covariance matrix deviates from the true one, which results in MUltiple SIgnal Classification (MUSIC) Direction-Of-Arrival (DOA) estimation performance breakdown. To deal with this problem, an iterative algorithm is proposed to improve the MUSIC performance by modifying the signal subspace in this paper. Firstly, the DOAs are roughly estimated based on the noise subspace obtained from sample covariance matrix. Then, considering the sparsity of signals and the low-rank property of steering matrix, a new signal subspace is got from the steering matrix consisting of estimated DOAs and their adjacent angles. Finally, the signal subspace is modified by solving an optimization problem. Simulation results demonstrate the proposed algorithm can improve the subspace estimation accuracy and furtherly improve the MUSIC DOA estimation performance, especially in small sample cases.
-
闫锋刚, 刘秋晨, 邵多, 等. 基于谱分解的降阶求根MUSIC算法[J]. 电子与信息学报, 2017, 39(10): 2421–2427. doi: 10.11999/JEIT170024YAN Fenggang, LIU Qiuchen, SHAO Duo, et al. Reduced-dimension Root-MUSIC algorithm based on spectral factorization[J]. Journal of Electronics &Information Technology, 2017, 39(10): 2421–2427. doi: 10.11999/JEIT170024 文才, 吴建新, 王彤, 等. 波束-多普勒酉ESPRIT多目标DOA估计[J]. 电子与信息学报, 2018, 40(5): 1136–1143. doi: 10.11999/JEIT170707WEN Cai, WU Jianxin, WANG Tong, et al. Multi-target DOA estimation using beam-doppler unitary ESPRIT[J]. Journal of Electronics &Information Technology, 2018, 40(5): 1136–1143. doi: 10.11999/JEIT170707 BELLILI F, ELGUET C, AMOR S B, et al. Code-aided DOA estimation from turbo-coded QAM transmissions: Analytical CRLBs and maximum likelihood estimator[J]. IEEE Transactions on Wireless Communications, 2017, 16(5): 2850–2865. doi: 10.1109/TWC.2017.2669026 STOICA P and NEHORAI A. MUSIC, maximum likelihood, and Cramer-Rao bound: Further results and comparisons[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1990, 38(12): 2140–2150. doi: 10.1109/29.61541 PILLAI S U and KWON B H. Forward/backward spatial smoothing techniques for coherent signal identification[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1989, 37(1): 8–15. doi: 10.1109/29.17496 VASYLYSHYN V. Removing the outliers in root-MUSIC via pseudo-noise resampling and conventional beamformer[J]. Signal Processing, 2013, 93(12): 3423–3429. doi: 10.1016/j.sigpro.2013.05.026 QIAN Cheng, HUANG Lei, and SO H C. Improved unitary root-MUSIC for DOA estimation based on pseudo-noise resampling[J]. IEEE Signal Processing Letters, 2014, 21(2): 140–144. doi: 10.1109/LSP.2013.2294676 VASYLYSHYN V I. DOA estimation using beamspace root-music based estimator bank[C]. The 11th International Conference on Antenna Theory and Techniques, Kiev, Ukraine, 2017: 367–369. SHAGHAGHI M and VOROBYOV S A. Subspace leakage analysis and improved DOA estimation with small sample size[J]. IEEE Transactions on Signal Processing, 2015, 63(12): 3251–3265. doi: 10.1109/TSP.2015.2422675 SHAGHAGHI M and VOROBYOV S A. Iterative root-MUSIC algorithm for DOA estimation[C]. The 5th IEEE International Workshop on Computational Advances in Multi-Sensor Adaptive Processing, St. Martin, France, 2013: 53–56. VINCENT F, PASCAL F, and BESSON O. A bias-compensated MUSIC for small number of samples[J]. Signal Processing, 2017, 138: 117–120. doi: 10.1016/j.sigpro.2017.03.015 WANG Cheng, TANG Jun, and YANG Bin. Fast and convenient implementation of iterative eigenspace-based beamforming[J]. Electronics Letters, 2015, 51(9): 720–722. doi: 10.1049/el.2015.0131 YI Shanchao, WU Ying, and WANG Yunlong. Projection-based robust adaptive beamforming with quadratic constraint[J]. Signal Processing, 2016, 122: 65–74. doi: 10.1016/j.sigpro.2015.11.016 NIE Weike, FENG Dazheng, XIE Hu, et al. Improved MUSIC algorithm for high resolution angle estimation[J]. Signal Processing, 2016, 122: 87–92. doi: 10.1016/j.sigpro.2015.12.002 WU Jianxin, WANG Tong, and BAO Zheng. Angle estimation for adaptive linear array using PCA-GS-ML estimator[J]. IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(1): 670–677. doi: 10.1109/TAES.2013.6404132 -






 下载:
下载:



 下载:
下载:
