Research on the Adaptive Synchrosqueezing Algorithm
-
摘要:
提高时频分辨率对多分量非平稳信号的分析与重建具有至关重要的作用。传统的时频分析方法由于窗口固定,分析频率变化较快的信号时存在时频聚集性不高的问题,无法自适应分辨多分量信号。该文针对频率快速变化信号,利用信号的局部信息特征,提出一种自适应的时频同步压缩变换算法。该方法有效提升了已有同步压缩变换时频分辨率,特别适用于频率接近且快速变换的多分量信号。同时,利用可分性条件,该文提出利用局部瑞利熵值对自适应窗口参数进行估计。最后,通过对合成信号和实测信号分析,证明了所提方法的可行性,对分析和重建复杂非平稳信号具有重要意义。
Abstract:The improvement of time-frequency resolution plays a crucial role in the analysis and reconstruction of multi-component non-stationary signals. For traditional time-frequency analysis methods with fixed window, the time-frequency concentration is low and hardly to distinguish the multi-component signals with fast-varying frequencies. In this paper, by adopting the local information of the signal, an adaptive synchrosqueezing transform is proposed for the signals with fast-varying frequencies. The proposed method is with high time-frequency resolution, superior to existing synchrosqueezing methods, and particularly suitable for multi-component signals with close and fast-varying frequencies. Meanwhile, by using the separability condition, the adaptive window parameters are estimated by local Rényi entropy. Finally, experiments on synthetic and real signals demonstrate the correctness of the proposed method, which is suitable to analyze and recover complex non-stationary signals.
-
张贤达, 保铮. 非平稳信号分析与处理[M]. 北京: 国防工业出版社, 1998: 1–3.ZHANG Xianda and BAO Zheng. Non-stationary Nonlinear Signal Analysis and Processing[M]. Beijing: National Defense Industry Press, 1998: 1–3. COHEN L. Time-frequency Analysis[M]. Englewood Cliffs: Prentice Hall, 1995: 44–195. FLANDRIN P. Time-Frequency/Time-Scale Analysis[M]. Cambridge: Academic Press, 1999: 1–386. DAUBECHIES I, LU Jianfeng, and WU H T. Synchrosqueezed wavelet transforms: An empirical mode decomposition-like tool[J]. Applied and Computational Harmonic Analysis, 2011, 30(2): 243–261. doi: 10.1016/j.acha.2010.08.002 HUANG N E, SHEN Zheng, LONG S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. The Royal Society A: Mathematical, Physical and Engineering Sciences, 1998, 454(1971): 903–995. doi: 10.1098/rspa.1998.0193 AUGER F and FLANDRIN P. Improving the readability of time-frequency and time-scale representations by the reassignment method[J]. IEEE Transactions on Signal Processing, 1995, 43(5): 1068–1089. doi: 10.1109/78.382394 OBERLIN T, MEIGNEN S, and PERRIER V. The Fourier-based synchrosqueezing transform[C]. 2014 IEEE International Conference on Acoustics, Speech and Signal Processing, Florence, Italy, 2014: 315–319. doi: 10.1109/ICASSP.2014.6853609. PHAM D H and MEIGNEN S. High-order synchrosqueezing transform for multicomponent signals analysis—With an application to gravitational-wave signal[J]. IEEE Transactions on Signal Processing, 2017, 65(12): 3168–3178. doi: 10.1109/TSP.2017.2686355 OBERLIN T and MEIGNEN S. The second-order wavelet synchrosqueezing transform[C]. 2017 IEEE International Conference on Acoustics, Speech and Signal Processing, New Orleans, USA, 2017: 3994–3998. doi: 10.1109/ICASSP.2017.7952906. WANG Shibin, CHEN Xuefeng, SELESNICK I W, et al. Matching synchrosqueezing transform: A useful tool for characterizing signals with fast varying instantaneous frequency and application to machine fault diagnosis[J]. Mechanical Systems and Signal Processing, 2018, 100: 242–288. doi: 10.1016/j.ymssp.2017.07.009 HERRY C L, FRASCH M, SEELY A J, et al. Heart beat classification from single-lead ECG using the synchrosqueezing transform[J]. Physiological Measurement, 2017, 38(2): 171–187. doi: 10.1088/1361-6579/aa5070 HE Kuanfang, LI Qi, and YANG Qing. Characteristic analysis of welding crack acoustic emission signals using synchrosqueezed wavelet transform[J]. Journal of Testing and Evaluation, 2018, 46(6): 2679–2691. doi: 10.1520/JTE20170218 LI Lin, CAI Haiyan, JIANG Qingtang, et al. An empirical signal separation algorithm for multicomponent signals based on linear time-frequency analysis[J]. Mechanical Systems and Signal Processing, 2019, 121: 791–809. doi: 10.1016/j.ymssp.2018.11.037 STANKOVIĆ L. A measure of some time-frequency distributions concentration[J]. Signal Processing, 2001, 81(3): 621–631. doi: 10.1016/S0165-1684(00)00236-X FUSCUS E. Digitized 2.5 microsecond echolocation pulse emitted by the Large Brown Bat[EB/OL]. https://www.ece. rice.edu/dsp/software/bat.shtml, 2017. -





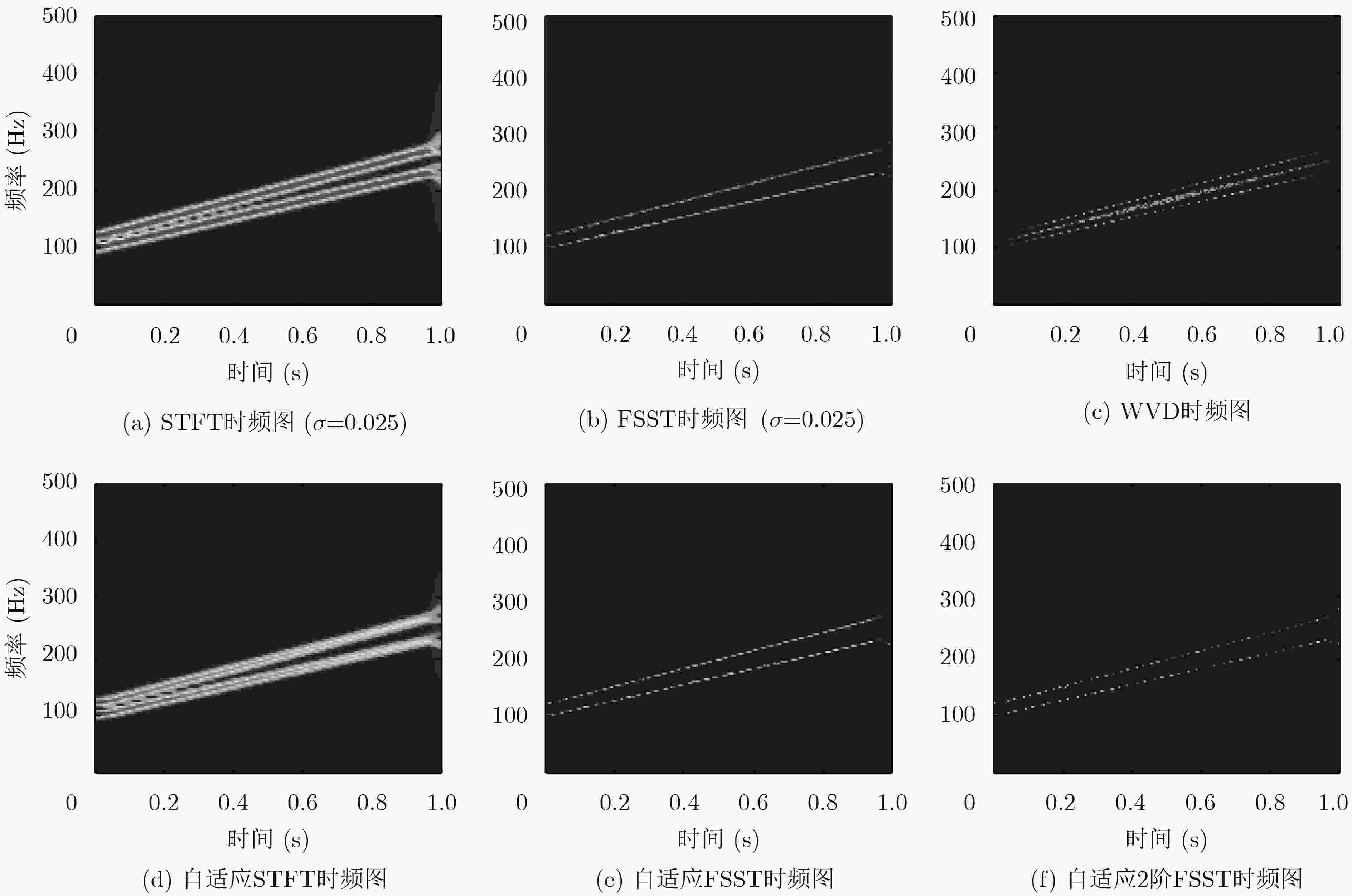
 下载:
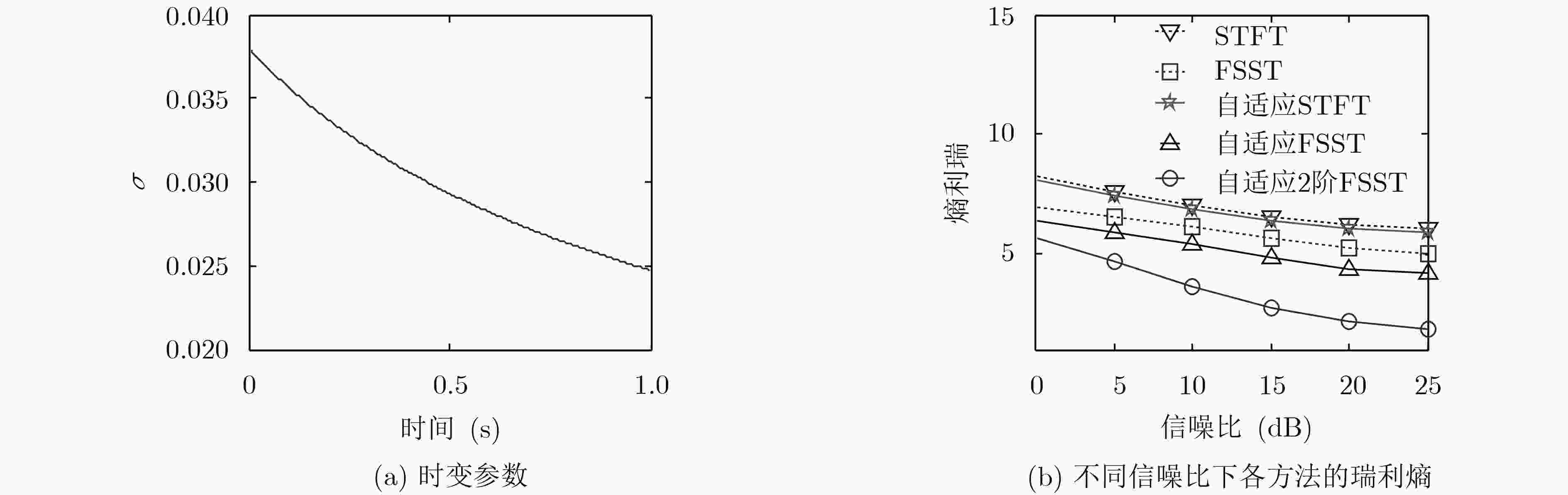
下载:
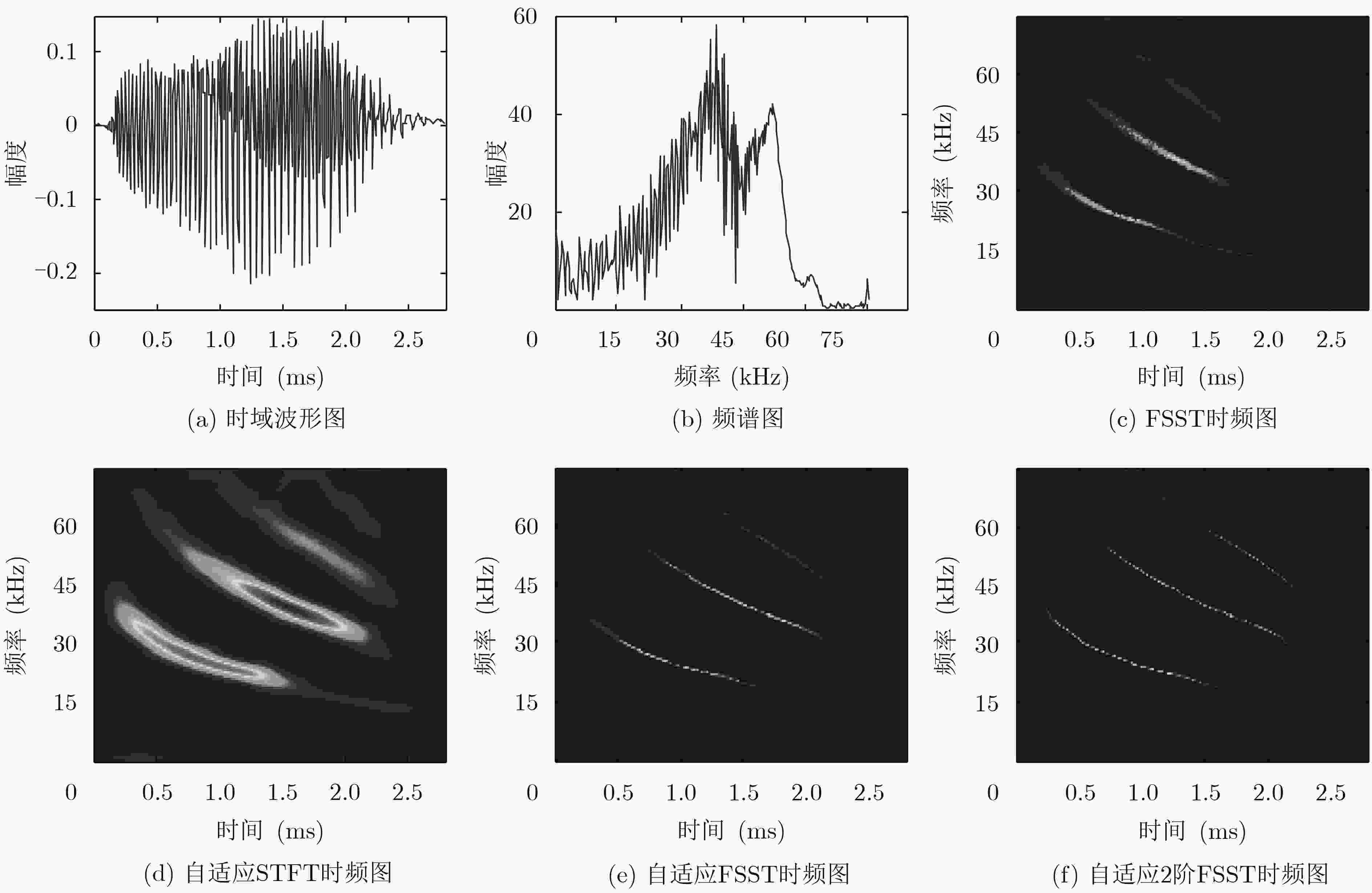


 下载:
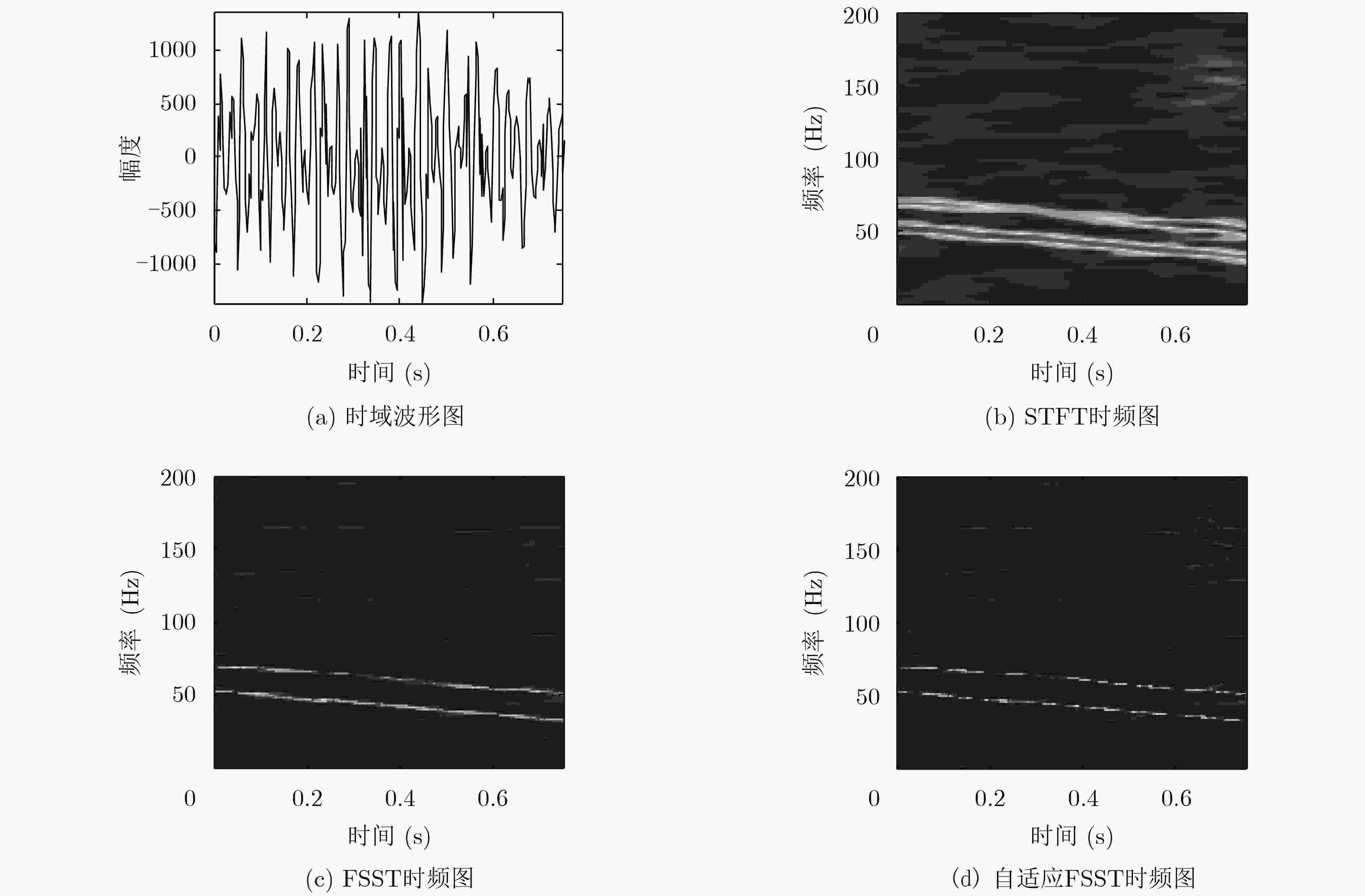
下载:
