Design and Implementation of Robust Particle Filter Algorithms under Student-t Measurement Distribution
-
摘要: 野值是一种异于总体数据的非高斯量测值,在实际传输中野值的加入常使信号出现厚尾特性。粒子滤波是基于贝叶斯框架的适用于非线性/非高斯系统的一种滤波方法。如果在量测噪声中存在野值会使粒子滤波的精度下降。该文利用学生t分布建模量测噪声模型,结合变分贝叶斯(VB)递推方法设计一种新颖的边缘粒子滤波(MPF-VBM),它在滤波同时可对量测噪声的包括均值在内的全部参数进行实时估计。进一步,利用该估计算法,在量测噪声时变条件下研究了噪声关联的粒子滤波算法(MPF-VBM-COR)。通过对典型单变量增长模型的仿真,验证了所提两种算法相比于已有算法在状态估计上具有更优越的鲁棒性。Abstract: Outliers are non-Gaussian measurement values far from the bulk of data. In practical transmission, the signals added with outlier often have the heavy-tailed property. Particle filter is based on the Bayesian framework and applicable to the non-linear and non-Gaussian system. However, measurement noise with outlier degrades the performance of particle filter. In this paper, student-t distribution is used to model the measurement noise, combined with Variational Bayes (VB), a novel particle filter Marginalized Particle Filter with VB Mean(MPF-VBM) is designed, which can estimate all parameters of t-distributed measurement distribution including mean parameter as well as state. Further, particle filter with noise correlation (MPF-VBM-COR) at the same epoch which is applicable to time variant measurement noise is developed. For verifying the performances of the proposed algorithms, the simulations on the typical univariate non-stationary growth model are performed under the different noise conditions in detail. The outcomes show that the proposed two algorithms of MPF-VBM and MPF-VBM-COR (MPF-VBM-Corrlation) have the superior performances to the compared ones.
-
Key words:
- Particle filter /
- Variational Bayes(VB) /
- Mean estimation /
- Noise correlation /
- Student-t distribution
-
表 1 基于VB带有噪声均值估计的边缘粒子滤波(MPF-VBM)算法
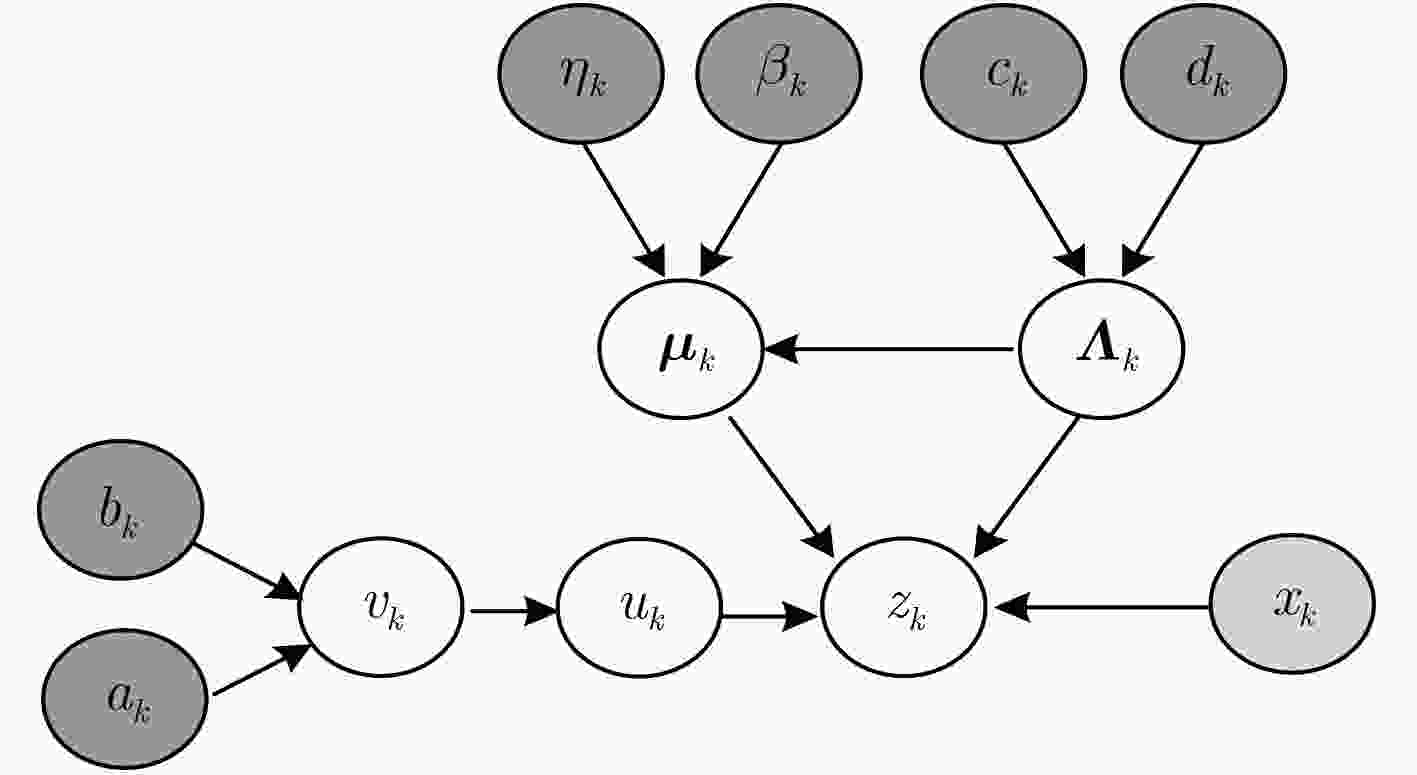
从分布${ {\text{N} } }\left( { { {\text{x} }_0}\left| { { {\text{m} }_{0\left| 0 \right.} },{ {\text{P} }_{0\left| 0 \right.} } } \right.} \right)$采样粒子${\text{x}}_0^{\left( i \right)}$$i = 1,2, ·\!·\!· ,N$,并且设置权值$\omega _0^{\left( i \right)} = {1 / N}$;初始化超参数$a_0^{\left( i \right)},\;\;b_0^{\left( i \right)},\;\;c_0^{\left( i \right)},\;\;d_0^{\left( i \right)},\nu _0^{\left( i \right)},\text{η} _0^{\left( i \right)}$和$\beta _0^{\left( i \right)}$;计算初
始参数${\text{μ} _0}$, ${\text{Λ} _0}$和${\nu _0}$期望。对时刻$k = 1,2, ·\!·\!· ,K$对每一个粒子$i = 1,2, ·\!·\!· ,N$ (1) 使用式(25)做噪声参数的时间更新;
(2) 从状态传递方程$p\left({\text{x} }_k^{\left( i \right)}\left| {\text{x} }_{k - 1}^{\left( i \right)} \right.\right)$做粒子的一步预测;(3) 通过新量测${{\text{z}}_k}$用式(15)更新重要性权值; (4) 必要的话,粒子重采样; (5) 使用式(13),式(14),式(16),式(17),式(18),式(19),式(22),式(23),并利用重采样粒子做噪声参数后验更新,
$\varTheta _{k\left| k \right.}^{\left( i \right)} = T\left( {\varTheta _{k\left| {k - 1} \right.}^{\left( i \right)},x_k^{\left( i \right)},{z_k}} \right)$;其中$T\left( \cdot \right)$代表参数充分统计量;得出当前的噪声参数期望值及对应状态值; 在$k = = K$前,进行下一次循环。 表 2 对应3种噪声的3种算法的均方根误差平均值(ARMSE)
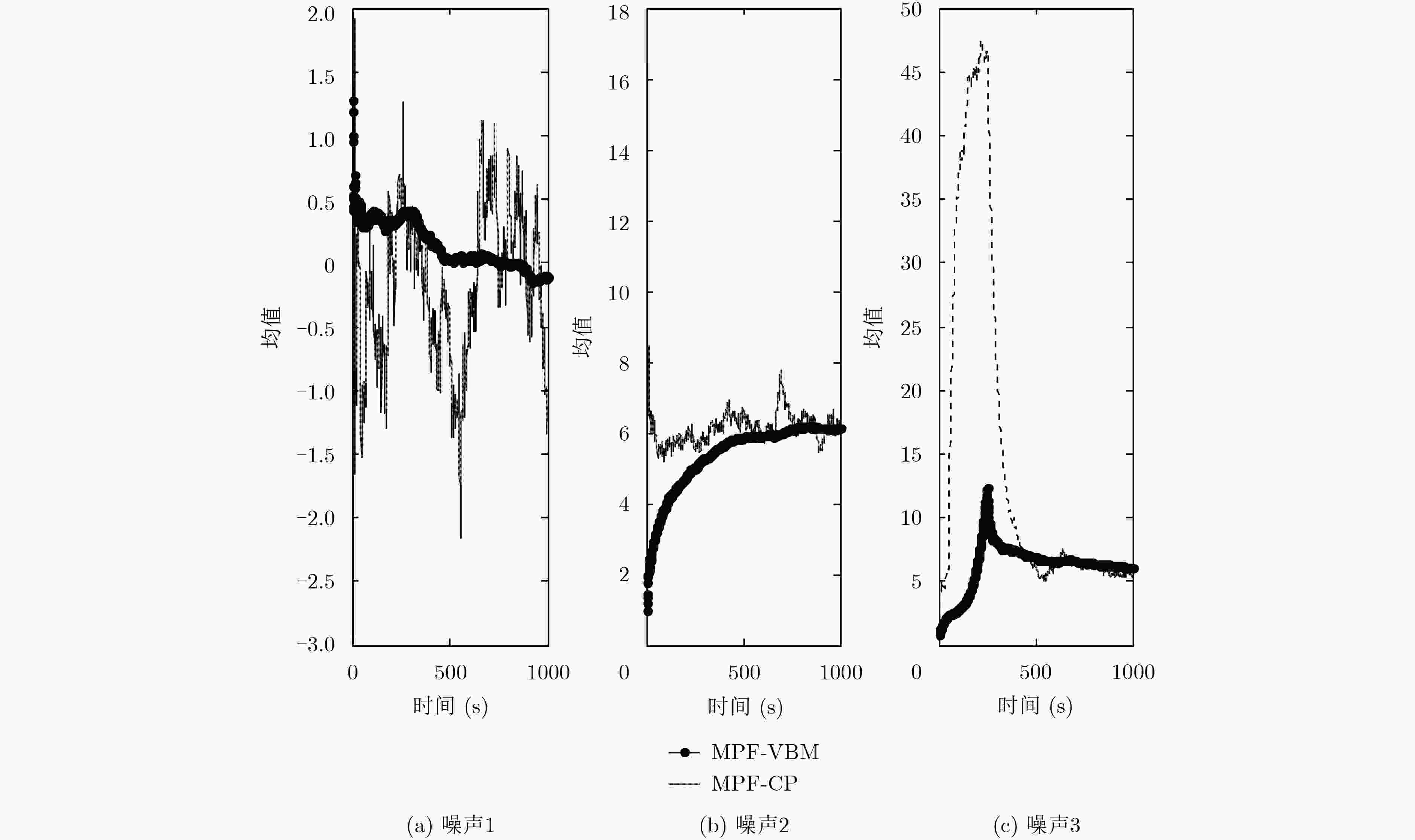
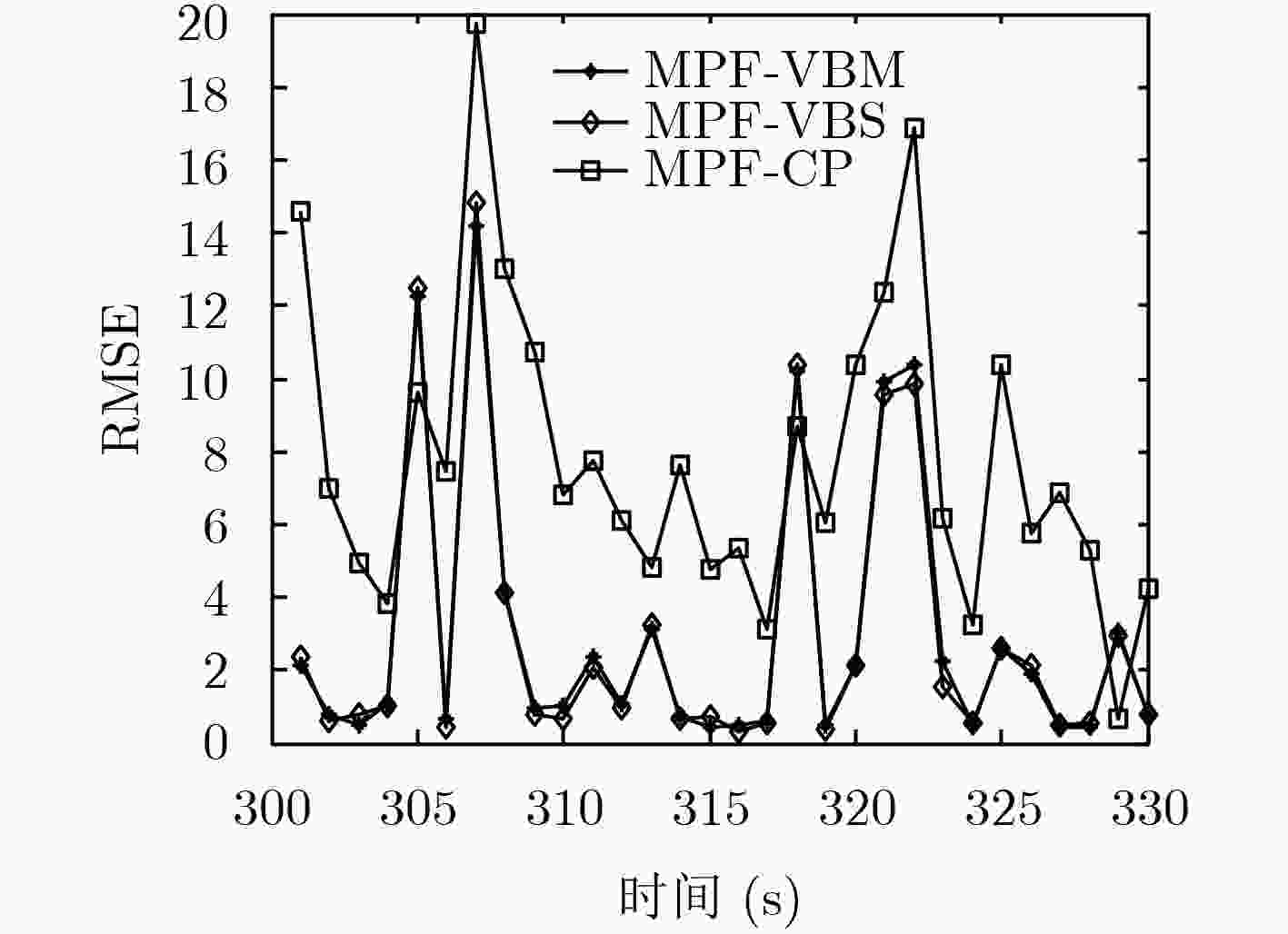
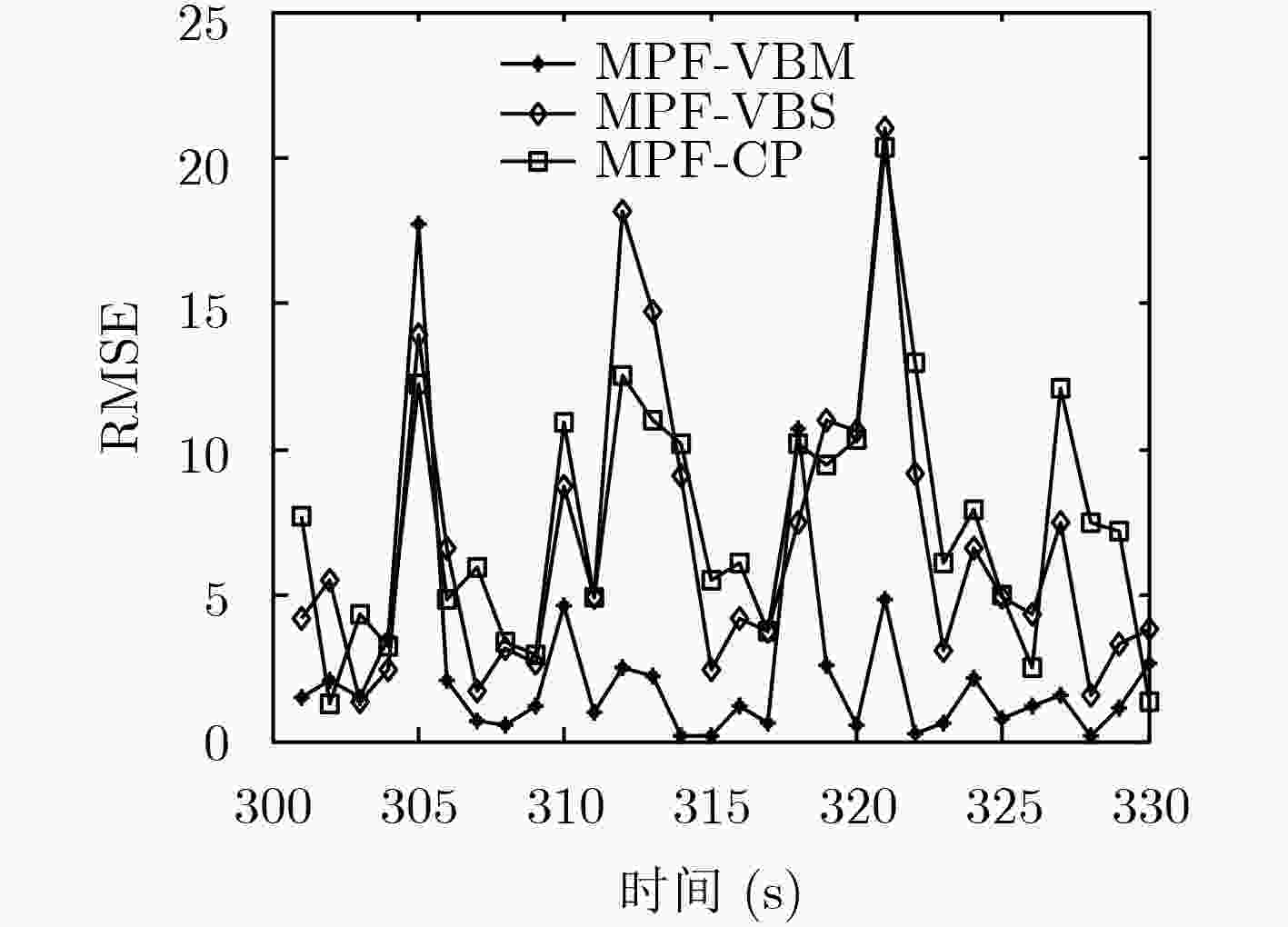
量测噪声 MPF-VBM MPF-VBS MPF-CP N(0,1)+20%U(–20, 20)野值 5.5673 5.5468 8.5571 N(6, 1)无野值 4.6170 8.1141 8.8132 N(6,5)+20%U(20, 60)野值 6.3353 8.6288 8.7588 运行时间(s) 0.01067 0.007187 0.005587 表 3 对应3种噪声的3种算法的均方根误差平均值(ARMSE)
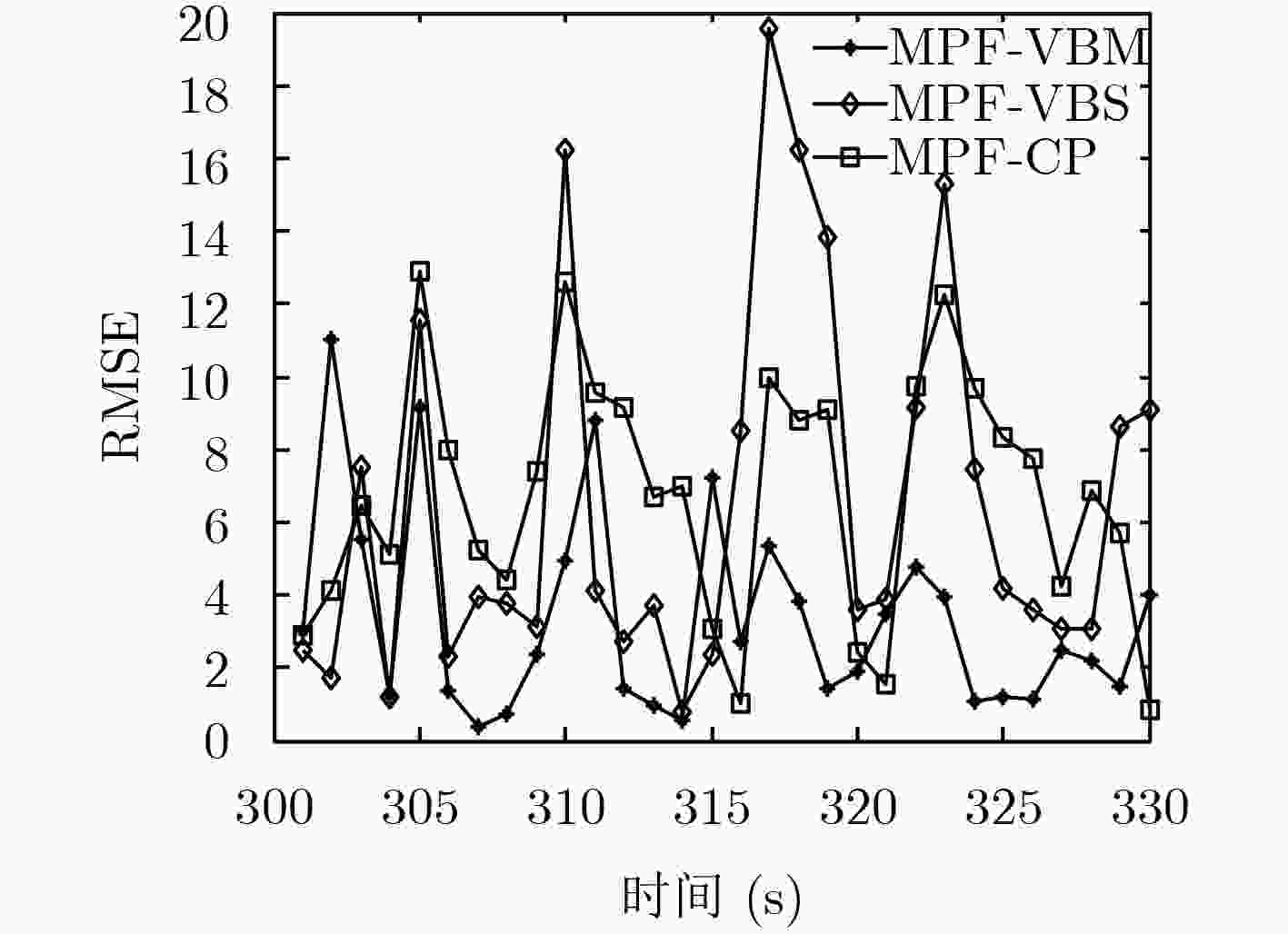
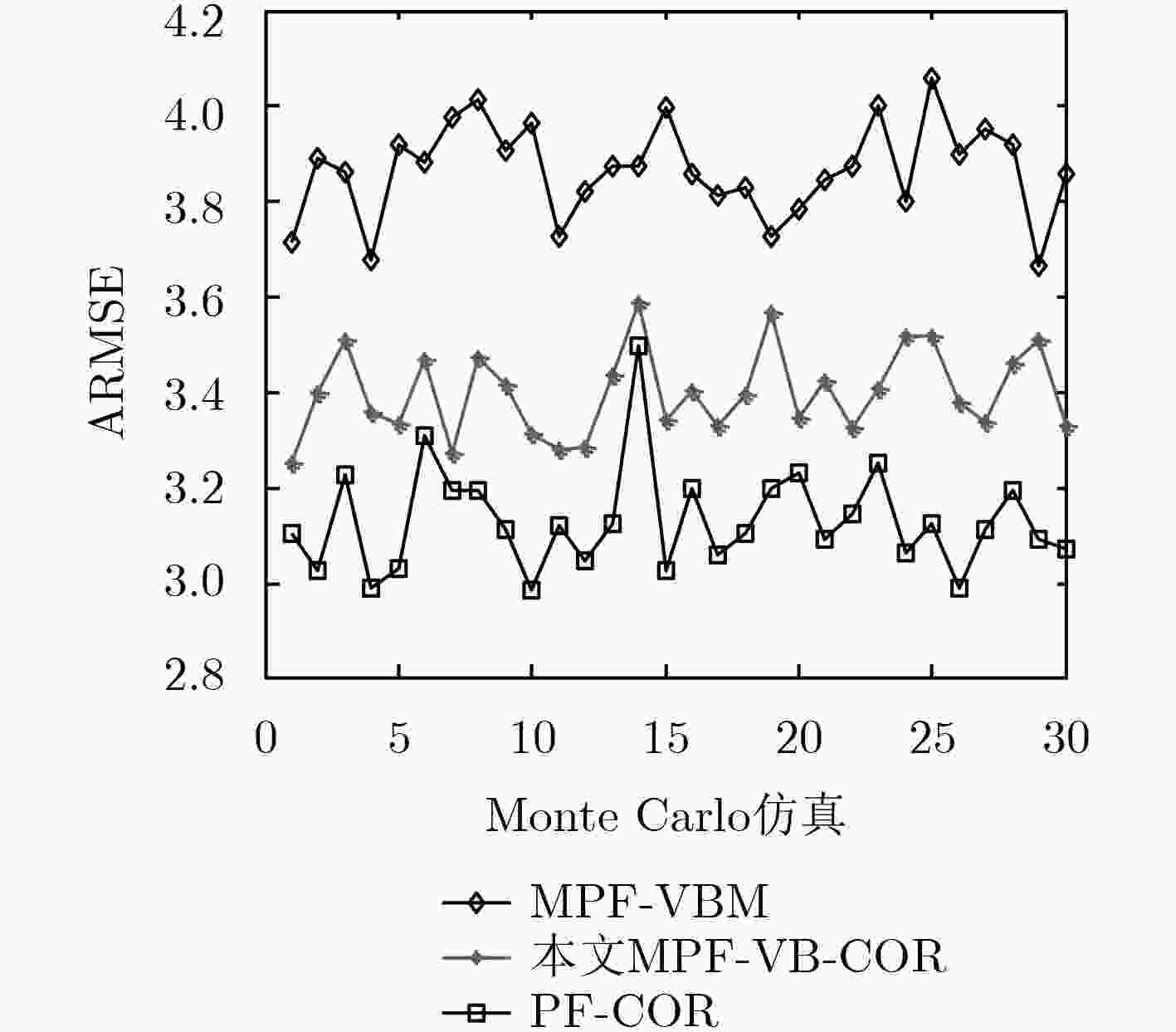
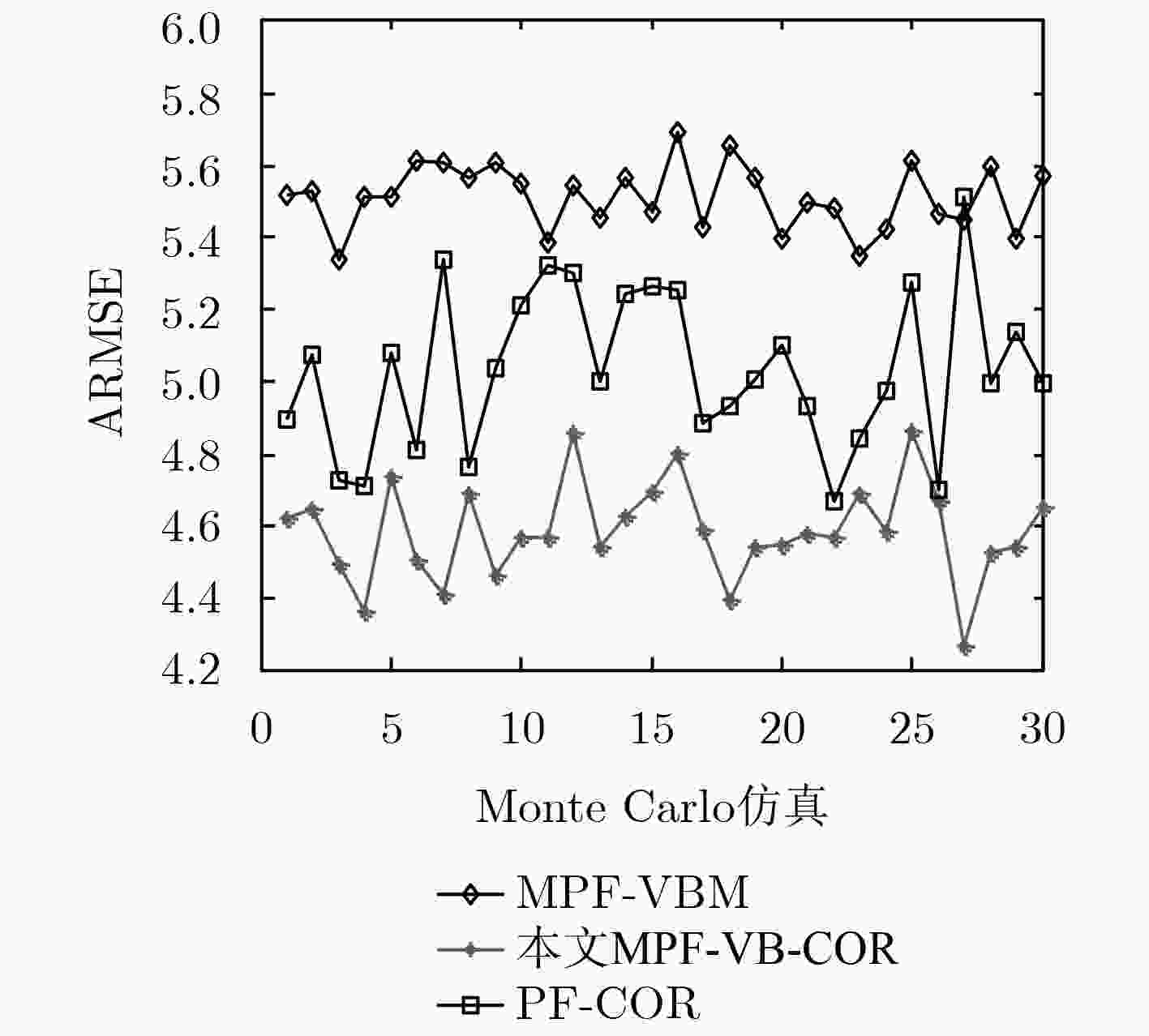
量测噪声 MPF-VBM MPF-VB-COR PF-COR ${{N} }\left( {0,\;{5 / 2} } \right)$ 3.8662 3.4025 3.1384 ${{N} }\left( {0,\;R} \right)$ $R$时变 5.5178 4.5536 5.0392 ${{N} }\left( {0,\;{5 / 2} } \right)$+20%
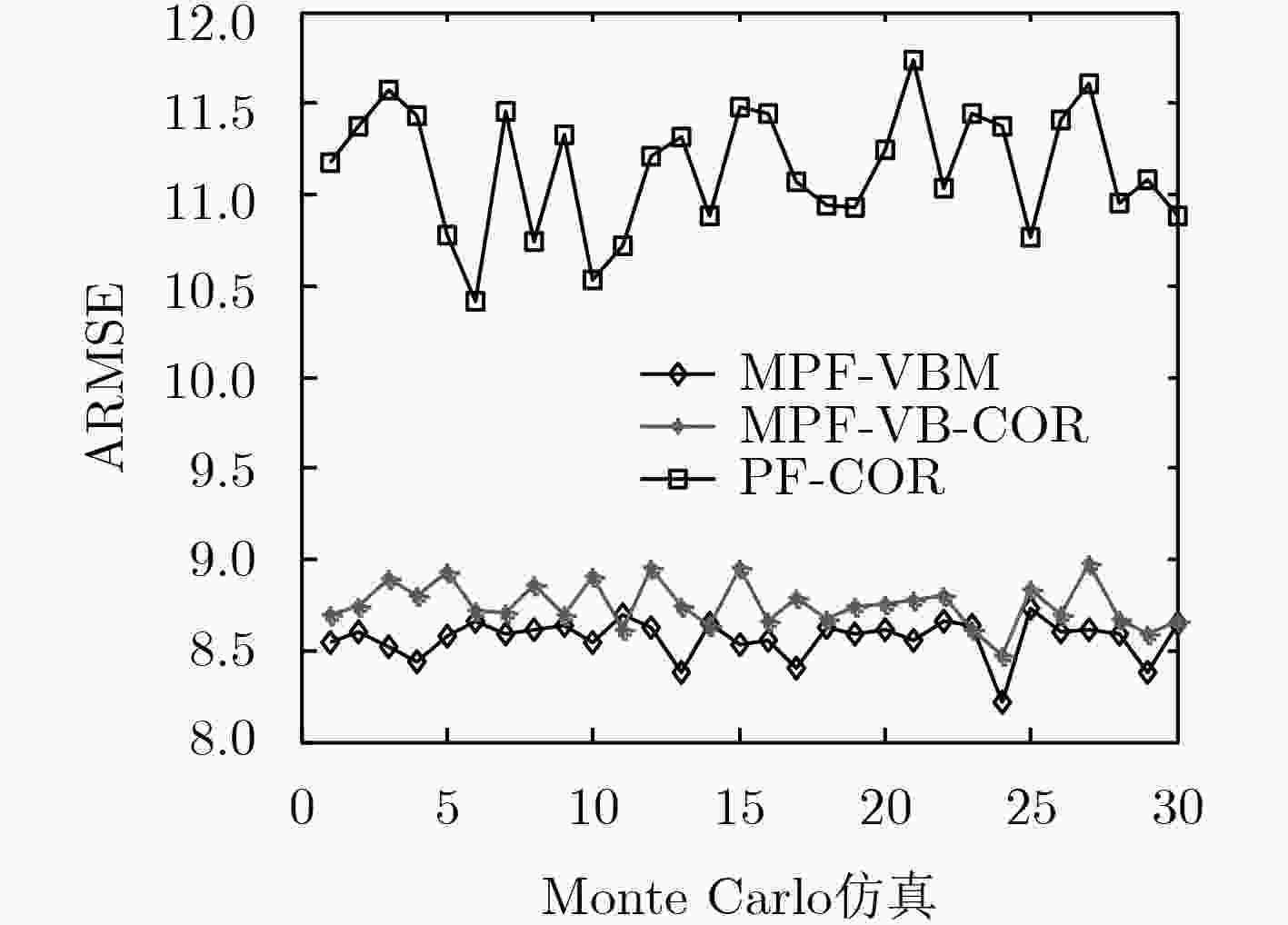
Unif (–5, 5)野值8.5892 8.7574 11.0393 -
XU Long, MA Kemao, LI Wenshuo, et al. Particle filtering for networked nonlinear systems subject to random one-step sensor delay and missing measurements[J]. Neurocomputing, 2018, 275: 2162–2169. doi: 10.1016/j.neucom.2017.10.059 STORVIK G. Particle filters for state-space models with the presence of unknown static parameters[J]. IEEE Transactions on Signal Processing, 2002, 50(2): 281–289. doi: 10.1109/78.978383 SAHA S, ÖZKAN E, GUSTAFSSON F, et al. Marginalized particle filters for Bayesian estimation of Gaussian noise parameters[C]. The 13th International Conference on Information Fusion, Edinburgh, UK, 2010: 1–8. doi: 10.1109/ICIF.2010.5712016. ÖZKAN E, ŠMÍDL V, SAHA S, et al. Marginalized adaptive particle filtering for nonlinear models with unknown time-varying noise parameters[J]. Automatica, 2013, 49(6): 1566–1575. doi: 10.1016/j.automatica.2013.02.046 ZHAO Yujia, FATEHI A, and HUANG Biao. Robust estimation of ARX models with time varying time delays using variational Bayesian approach[J]. IEEE Transactions on Cybernetics, 2018, 48(2): 532–542. doi: 10.1109/TCYB.2016.2646059 PICHÉ R, SÄRKKÄ S, and HARTIKAINEN J. Recursive outlier-robust filtering and smoothing for nonlinear systems using the multivariate student-t distribution[C]. 2012 IEEE International Workshop on Machine Learning for Signal Processing, Santander, Spain, 2012: 1–6. doi: 10.1109/MLSP.2012.6349794. ZHANG Yonggang, JIA Guangle, LI Ning, et al. A novel adaptive Kalman filter with colored measurement noise[J]. IEEE Access, 2018, 6: 74569–74578. doi: 10.1109/ACCESS.2018.2883040 HUANG Yulong, ZHANG Yonggang, LI Ning, et al. A novel robust Student's t-based Kalman filter[J]. IEEE Transactions on Aerospace and Electronic Systems, 2017, 53(3): 1545–1554. doi: 10.1109/TAES.2017.2651684 XU Dingjie, SHEN Chen, and SHEN Feng. A robust particle filtering algorithm with non-Gaussian measurement noise using student-t distribution[J]. IEEE Signal Processing Letters, 2014, 21(1): 30–34. doi: 10.1109/LSP.2013.2289975 AIT-EL-FQUIH B and HOTEIT I. A variational Bayesian multiple particle filtering scheme for large-dimensional systems[J]. IEEE Transactions on Signal Processing, 2016, 64(20): 5409–5422. doi: 10.1109/TSP.2016.2580524 GAO Wei, LI Jingchun, ZHOU Guangtao, et al. Adaptive Kalman filtering with recursive noise estimator for integrated SINS/DVL systems[J]. The Journal of Navigation, 2015, 68(1): 142–161. doi: 10.1017/S0373463314000484 ZHU Hao, LEUNG H, and HE Zhongshi. State estimation in unknown non-Gaussian measurement noise using variational Bayesian technique[J]. IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(4): 2601–2614. doi: 10.1109/TAES.2013.6621839 CHEN J and MA L. Particle filtering with correlated measurement and process noise at the same time[J]. IET Radar, Sonar & Navigation, 2011, 5(7): 726–730. doi: 10.1049/iet-rsn.2010.0365 SAHA S and GUSTAFSSON F. Particle filtering with dependent noise processes[J]. IEEE Transactions on Signal Processing, 2012, 60(9): 4497–4508. doi: 10.1109/TSP.2012.2202653 WANG Zongyuan and ZHOU Weidong. Robust linear filter with parameter estimation under student-t measurement distribution[J]. Circuits, Systems, and Signal Processing, 2019, 38(6): 2445–2470. doi: 10.1007/s00034-018-0972-8 -





 下载:
下载:


 下载:
下载:
