Performance of Rank Sum Nonparametric Detector at Clutter Edge
-
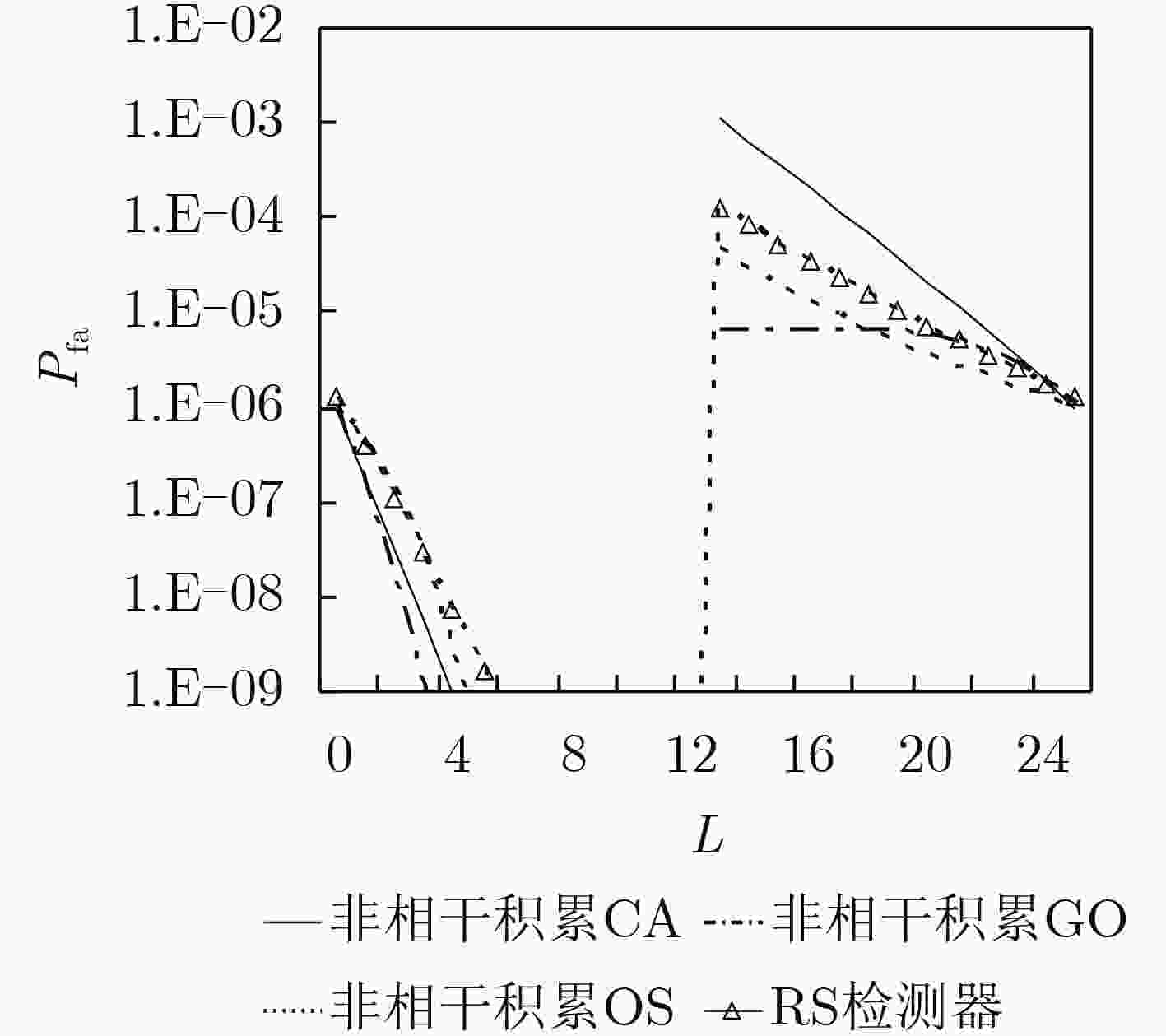
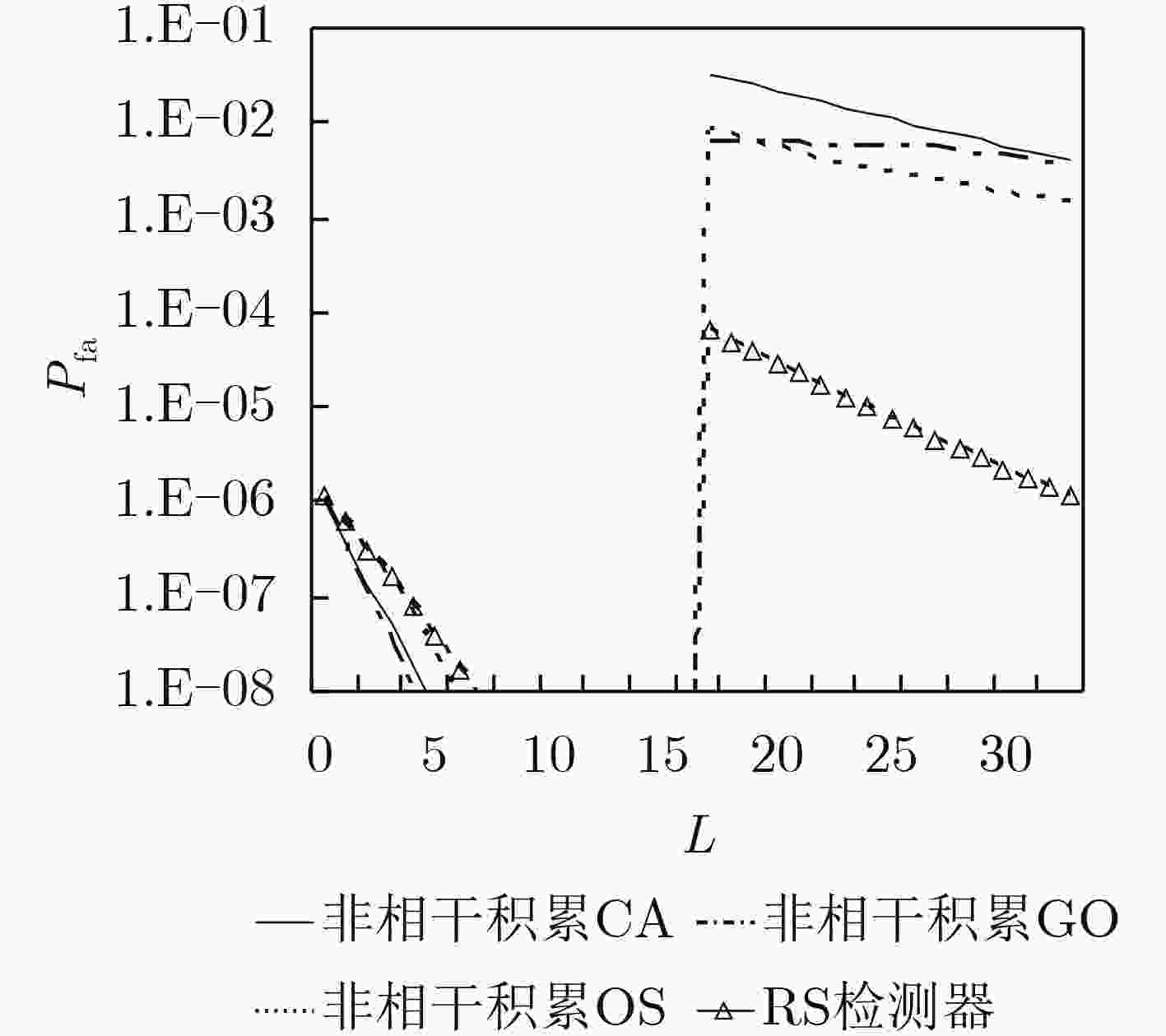
摘要: 人们常用Rohling教授提出的3种典型背景即均匀背景、多目标和杂波边缘来对检测器的恒虚警率(CFAR)性能进行衡量,但在现有的文献中缺乏秩和(RS)非参数检测器在杂波边缘中虚警概率的解析表达式,缺乏RS检测器与经典的参量型恒虚警率(CFAR)检测器在杂波边缘中虚警控制能力的比较,这在理论研究上是不完整、不全面的。该文给出了RS检测器在杂波边缘中虚警概率的解析表达式,并比较了它与非相干积累单元平均(CA),选大(GO)和有序统计(OS)恒虚警方法在杂波边缘中的虚警控制能力。可以看出,在强、弱杂波均为瑞利分布的情况下,RS检测器在杂波边缘的虚警控制能力处于非相干积累CA方法和非相干积累OS方法之间。但是当长拖尾分布的非高斯杂波进入参考滑窗时,非相干积累CA, GO和OS参量型检测方法的虚警概率都产生了3个以上数量级的上升,且不能回到原始设定的虚警概率。而RS检测器显示出了非参量检测器的优势,即当杂波背景的分布类型发生变化后,它仍然可以保持虚警概率的恒定。Abstract: The performance of a Constant False Alarm Rate (CFAR) detector is often evaluated in three typical backgrounds - homogeneous environment, multiple targets situation and clutter edges described by Prof. Rohling. However, there is a lack of the analytic expression of the false alarm rate for the Rank Sum (RS) nonparametric detector at clutter boundaries, and lack of a comparison of the ability for the RS detector to control the rise of the false alarm rate at clutter edges to that of the conventional parametric CFAR schemes; which is incomplete and imperfect for the detection theory of nonparametric detectors. The analytic expression of the false alarm rate Pfa for the RS nonparametric detector at clutter edges is given in this paper, and the ability of the RS nonparametric detector to control the rise of the false alarm rate at clutter edges is compared to that of the Cell Averaing (CA) CFAR, the Greatest Of (GO) CFAR and the Ordered Statistic (OS) CFAR with incoherent integration. When both of the heavy and the weak clutters follow a Rayleigh distribution, it is shown that the rise of the false alarm rate for the RS detector at clutter edges lies between that of the CA-CFAR and that of the OS-CFAR with incoherent integration. If a non-Gaussian distributed clutter with a long tail moves into the reference window, the rise of the CA-CFAR, the GO-CFAR and the OS-CFAR with incoherent integration reaches a peak of more than 3 orders of magnitude, and can not return to the original pre-designed Pfa. However, the RS nonparametric detector exhibits its inherent advantage in such situation, it can maintain a constant false alarm rate even the distribution form of clutter becomes a different one.
-
Key words:
- Radar /
- Target detection /
- Nonparametric /
- Weibull distribution /
- Constant False Alarm Rate (CFAR)
-
WEINBERG G V and TRAN C. A Weber-Haykin detector in correlated Pareto distributed clutter[J]. Digital Signal Processing, 2019, 84: 107–113. doi: 10.1016/j.dsp.2018.10.007 WEINBERG G V, BATEMAN L, and HAYDEN P. Development of non-coherent CFAR detection processes in Weibull background[J]. Digital Signal Processing, 2018, 75: 96–106. doi: 10.1016/j.dsp.2018.01.002 ZHOU Wei, XIE Junhao, LI Gaopeng, et al. Robust CFAR detector with weighted amplitude iteration in nonhomogeneous sea clutter[J]. IEEE Transactions on Aerospace and Electronic Systems, 2017, 53(3): 1520–1535. doi: 10.1109/TAES.2017.2671798 MENG X W. Performance analysis of OS-CFAR with binary integration for Weibull background[J]. IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(2): 1357–1366. doi: 10.1109/TAES.2013.6494420 BAADECHE M and SOLTANI F. Performance analysis of mean level constant false alarm rate detectors with binary integration in Weibull background[J]. IET Radar, Sonar & Navigation, 2015, 9(3): 233–240. doi: 10.1049/iet-rsn.2014.0053 WEINBERG G V and KYPRIANOU R. Optimised binary integration with order statistic CFAR in Pareto distributed clutter[J]. Digital Signal Processing, 2015, 42: 50–60. doi: 10.1016/j.dsp.2015.04.002 WICKS M C and BALDYGO W J. Expert system CFAR: Algorithm development, experimental demonstration, and transition to airborne radar systems[J]. IEEE Aerospace and Electronic Systems Magazine, 2017, 32(9): 40–47. doi: 10.1109/MAES.2017.160243 ROHLING H. Radar CFAR thresholding in clutter and multiple target situations[J]. IEEE Transactions on Aerospace and Electronic Systems, 1983, AES-19(4): 608–621. doi: 10.1109/TAES.1983.309350 GANDHI P P and KASSAM S A. Analysis of CFAR processors in nonhomogeneous background[J]. IEEE Transactions on Aerospace and Electronic Systems, 1988, 24(4): 427–445. doi: 10.1109/7.7185 孟祥伟. 非参数秩和检测器的性能分析[J]. 电子与信息学报, 2013, 35(8): 2029–2032.MENG Xiangwei. Performance analysis of rank sum nonparametric detector[J]. Journal of Electronics &Information Technology, 2013, 35(8): 2029–2032. -





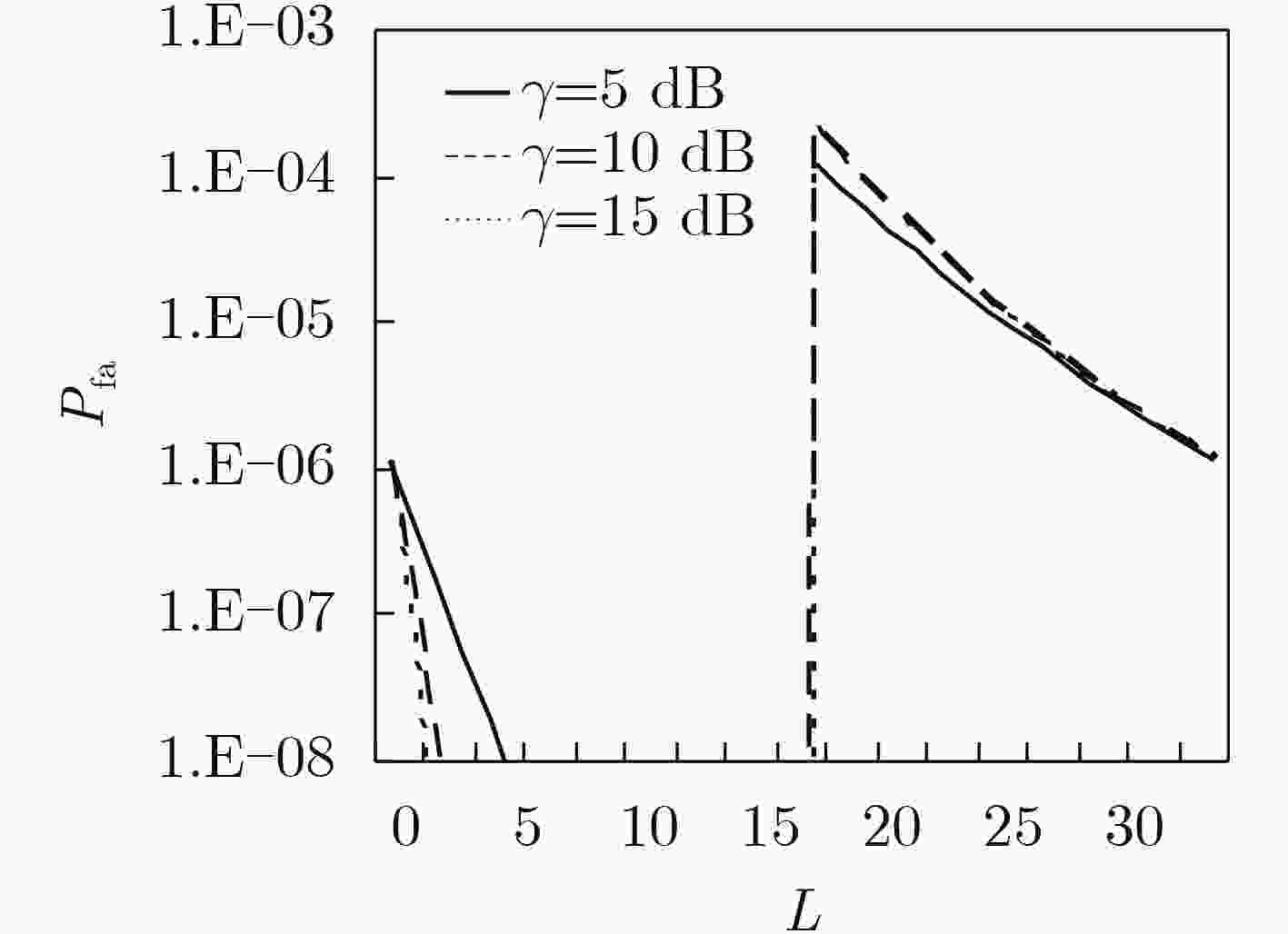
 下载:
下载:
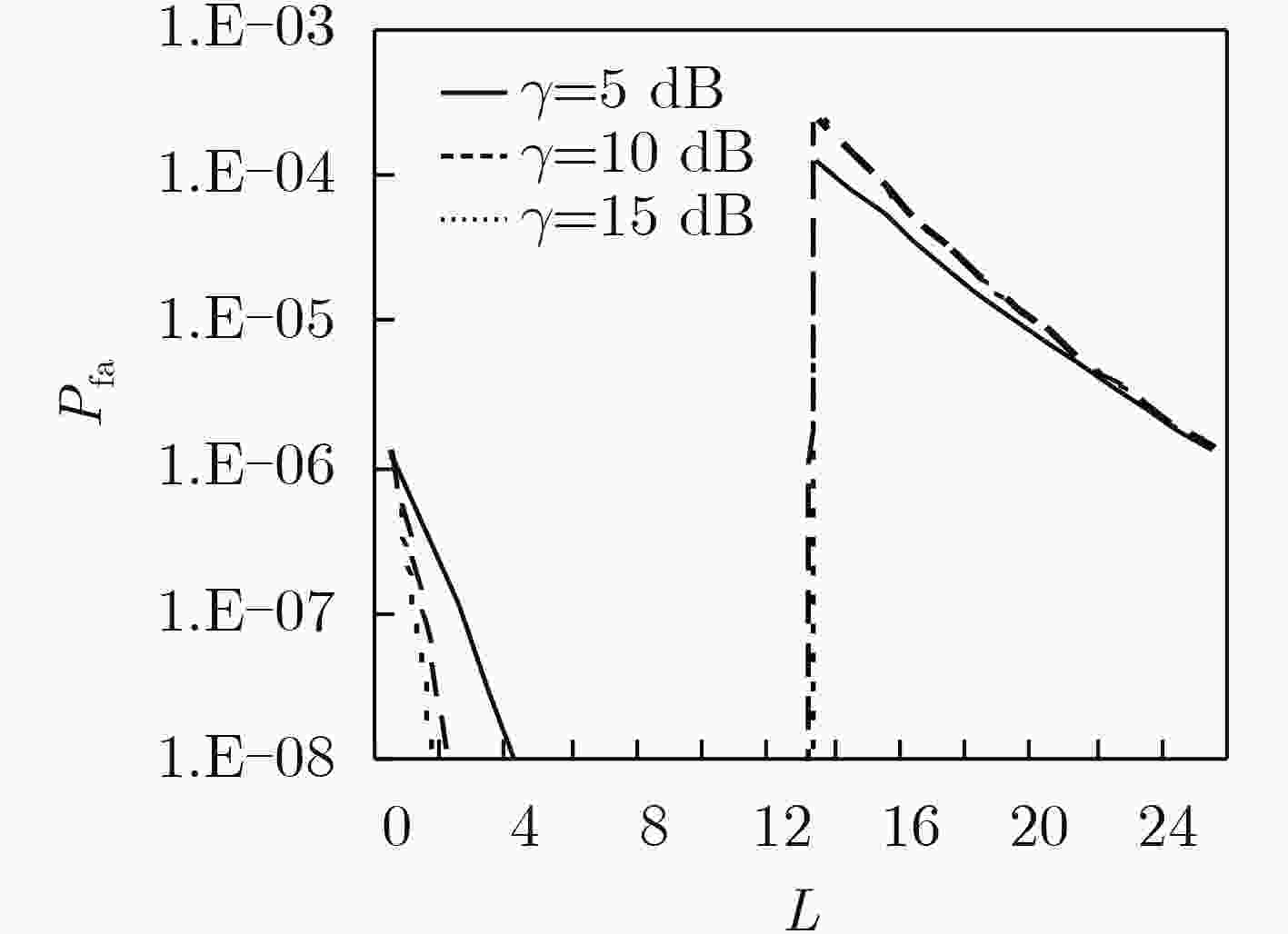
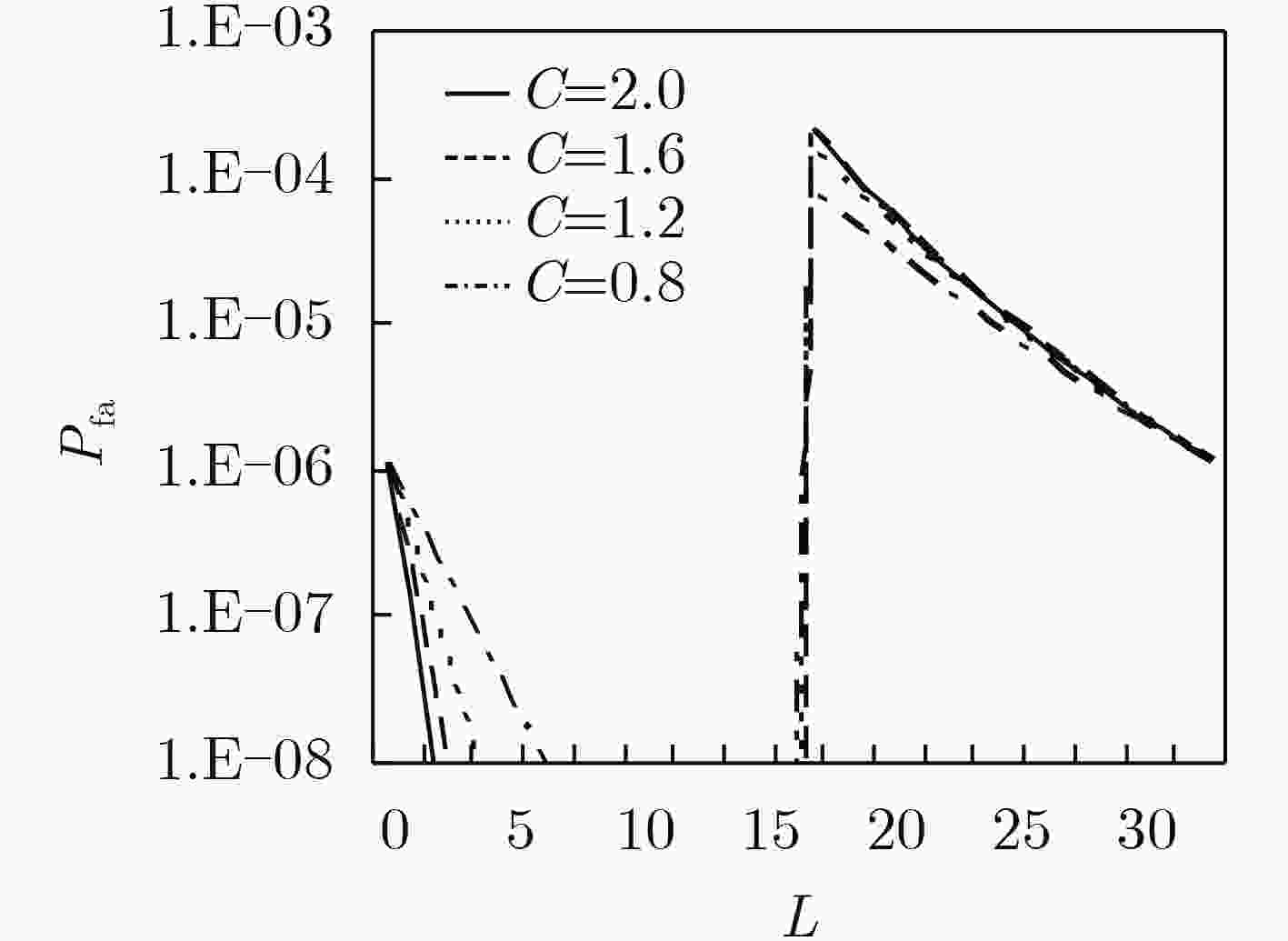
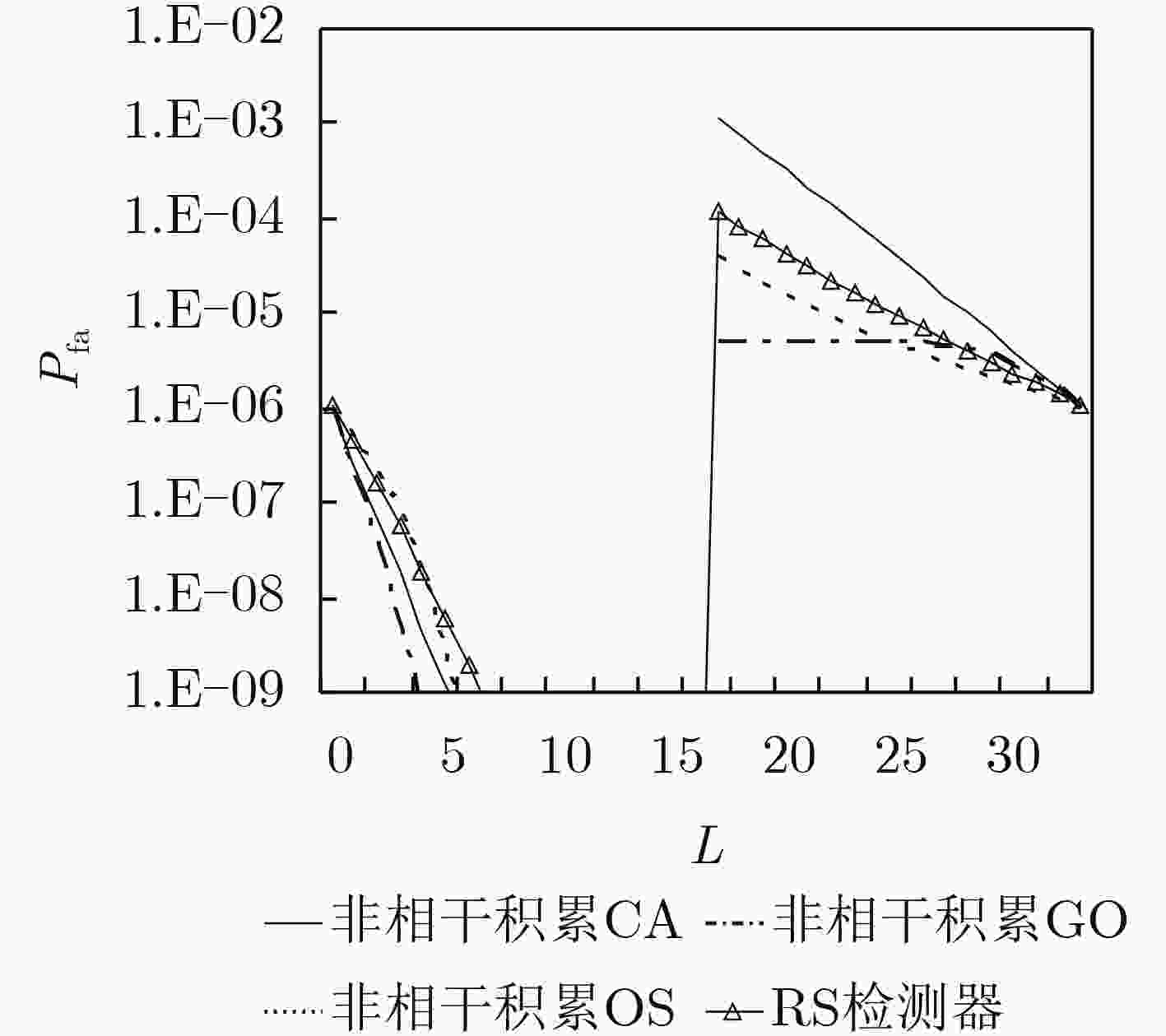


 下载:
下载:
