Conditional Empirical Mode Decomposition and Serial Parallel CNN for ElectroEncephaloGram Signal Recognition
-
摘要:
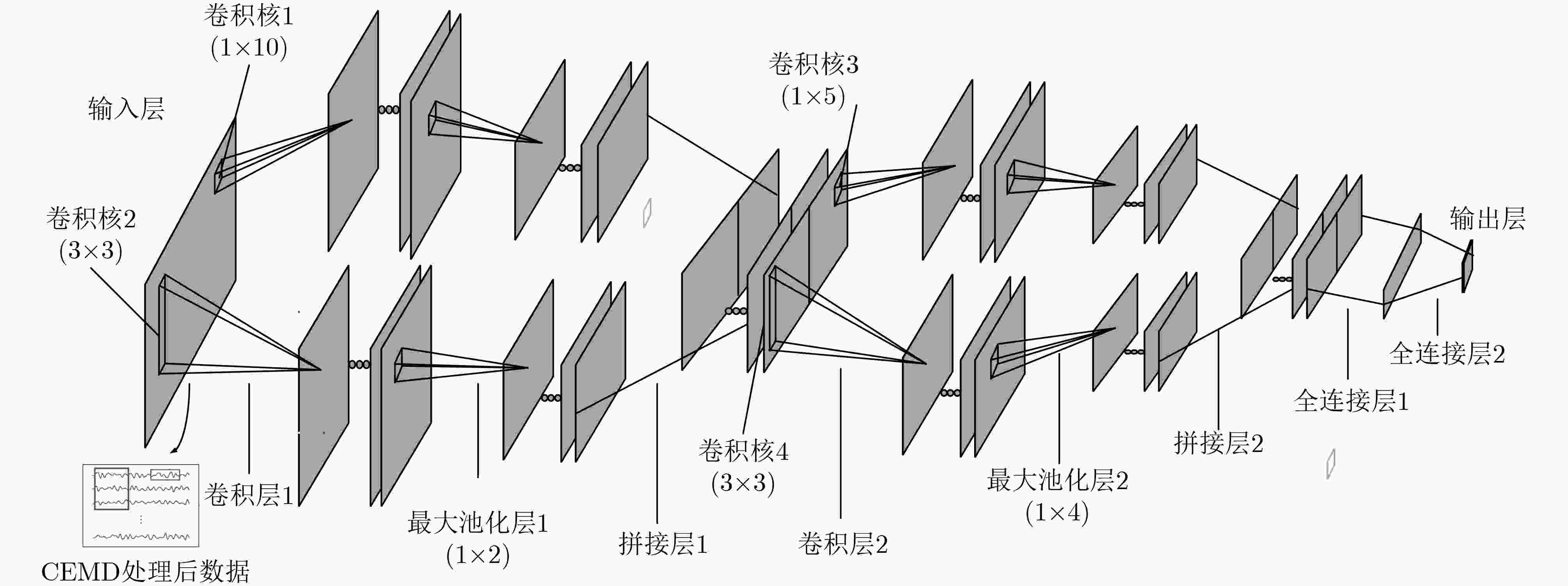
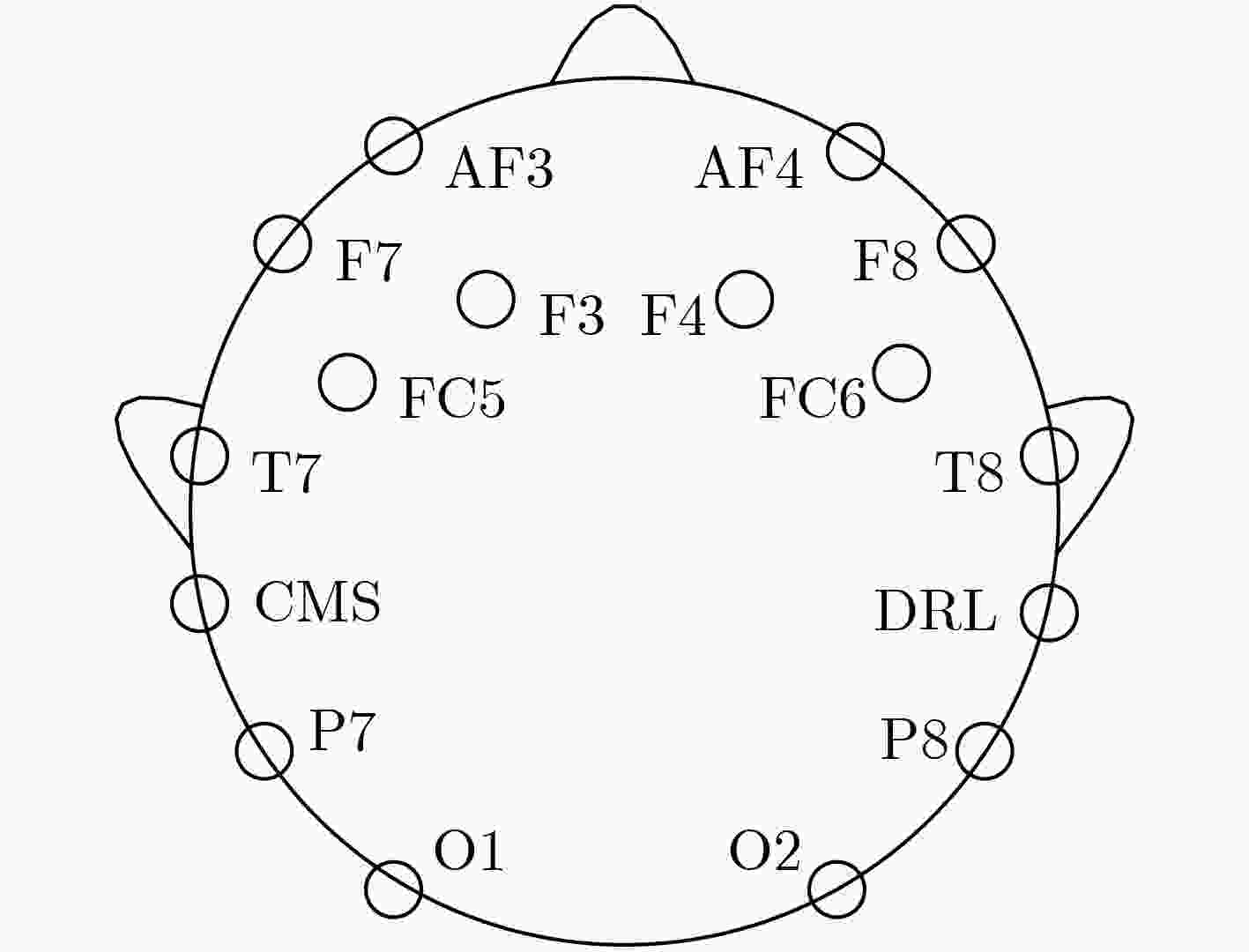
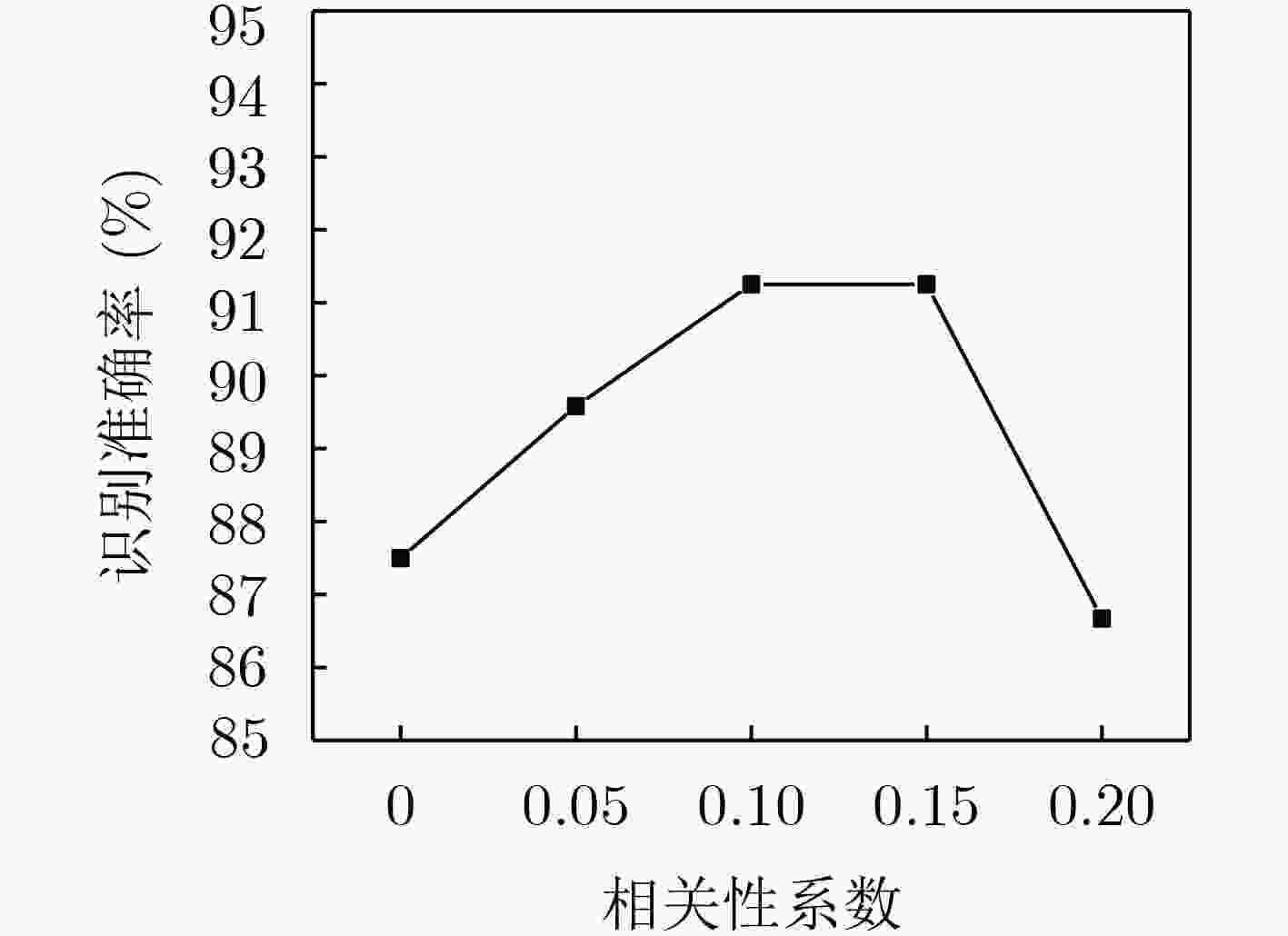
针对运动想象脑电信号(EEG)的非线性、非平稳特点，该文提出一种结合条件经验模式分解(CEMD)和串并行卷积神经网络(SPCNN)的脑电信号识别方法。在CEMD过程中，采用各阶固有模式分量(IMF)与原始信号的相关性系数作为第1个IMF筛选条件，在此基础上，提出各阶IMF之间的相对能量占有率作为第2个IMF筛选条件。此外，为了考虑脑电信号各个通道之间的特征和突出每个通道内的特征，该文提出SPCNN网络模型对进行CEMD过程后的脑电信号进行分类。实验结果表明，在自行采集的脑电数据集上平均识别率达到94.58%。在公开数据集BCI competition IV 2b上平均识别率达到82.13%，比卷积神经网络提高了3.85%。最后，在自行设计的智能轮椅脑电控制平台上进行了轮椅前进、左转和右转在线控制实验，验证了该文算法对脑电信号识别的有效性。
Abstract:For the non-linear and non-stationary characteristics of motor imagery ElectroEncephaloGram (EEG) signals, an EEG signal recognition method based on Conditional Empirical Mode Decomposition (CEMD) and Serial Parallel Convolutional Neural Network (SPCNN) is proposed. In the CEMD process, the correlation coefficient between the Intrinsic Mode Functions (IMFs) and the original signal is used as the first condition to select IMFs. Based on this, the relative energy occupancy rates between the IMFs are proposed as the second condition to select IMFs. Further, to consider the characteristics between the EEG signal channels and highlight the features in each EEG signal channel, a SPCNN model is proposed to classify the processed EEG signals. The experimental results show that the average recognition rate reaches 94.58% on the dataset collected by ourselves. And the average recognition rate reaches 82.13% on the BCI competition IV 2b dataset, which is 3.85% higher than the average recognition rate of convolutional neural network. Finally, the online control experiments are carried out on the designed intelligent wheelchair platform, which proves the effectiveness of the proposed algorithm for EEG signals recognition.
-
1. 引言
脑机接口(Brain-Computer Interface, BCI)直接把从人类头皮记录的大脑活动转换为计算机控制信号，并用来控制外部设备，从而在一定程度上帮助运动功能障碍者修复与外界的信息交流能力[1-3]。目前BCI系统已经受到很多关注，已有使用脑电控制智能轮椅[4]、机械手臂[5]等方面的研究。在BCI系统中，脑电信号(ElectroEncephaloGram, EEG)的特征提取和分类是最为关键的技术，但是由于EEG信号的非线性、非平稳特性，导致其识别较为困难[6]。
目前，研究者已经提出了许多经典的脑电信号特征提取方法，如：小波变换[7]、共空间模式(Common Spatial Pattern, CSP)[8,9]以及经验模式分解(Empirical Mode Decomposition, EMD)[10,11]等。其中，EMD能够自适应地分解信号，因而非常适合具有非线性、非平稳特征的脑电信号的分析。文献[10]采用了EMD算法来去除脑电信号中的噪音，但是脑电信号具有个体差异性，在该研究中，凭借经验选择固有模式分量(Intrinsic Mode Function, IMF)来重构脑电信号会导致某些重构后的脑电信号样本中混入多余的信息或者丢失掉重要的信息。此外，在这些传统的方法中，提取的特征通常是人为设计的，这带来了提取特征依赖研究者的专业知识，操作复杂以及识别率较低等问题。
由于深度网络模型强大的特征学习能力，一些深度学习方法[12-14]也被用于运动想象脑电信号的识别。卷积神经网络(Convolutional Neural Network, CNN)是其中一种典型代表，文献[12]提出了一种端到端的CNN模型，并且证明该模型非常适用于小样本的脑电信号识别。在文献[13]中，Zhang等人通过短时傅里叶变换(Short-Time Fourier Transform, STFT)将EEG信号转换为时频图像，然后将这些图像输入到CNN中进行分类，进一步提高了脑电信号的识别准确率。但是对于多通道脑电信号，每个通道的脑电信号之间是具有相关性的，以上的研究中提取的特征不能突出表现脑电信号通道之间的相关性，这会使得脑电信号中的有效信息不能得到充分的利用。
针对上述问题，本文提出了一种结合条件经验模式分解(Conditional Empirical Mode Decomposition, CEMD)和串并行卷积神经网络(Serial Parallel Convolutional Neural Network, SPCNN)的方法CEMD-SPCNN来识别EEG信号。在多个脑电数据集上得到的结果表明，本文方法能够提高脑电信号的识别准确率。本文的主要贡献包括：(1)提出CEMD算法以克服传统EMD算法凭借经验选择IMF的问题，采用各阶IMF与原始信号的相关性系数作为第1个IMF筛选条件，并提出各阶IMF之间的相对能量占有率作为第2个IMF筛选条件，通过CEMD算法对脑电信号进行重构，从而在一定程度上去除脑电信号中的噪音；(2)为了自动地从脑电信号中提取出有效特征，并且考虑到脑电信号的多通道特性，提出采用并列双卷积核的SPCNN对经过CEMD算法处理后的EEG信号进行识别，其中一个卷积核提取各个通道内部的特征，另一个卷积核注重提取多通道之间的相关性特征，从而充分提取脑电信号中的有效特征；(3)自行设计了脑电控制智能轮椅平台，并在该平台上进行了轮椅在线控制实验，进一步验证了所提方法的有效性。
2. 条件经验模式分解算法
2.1 经验模式分解
经验模式分解[15,16]是一种能够自适应地对信号进行处理，非常适合非线性、非平稳信号的分解算法。EMD的原理是将复杂的信号分解为有限多个固有模态函数和一个残余分量。分解得到的各阶IMF必须要满足两个约束条件：(1)在整个的信号数据中，极值点的个数和过零点的个数应该相等或者至多相差一个；(2)对于信号的任意一点，由局部极大值确定的上包络和由局部极小值确定的下包络的平均值必须为0。原始信号x(t)可以重建为多个IMF和剩余分量的组合，即
$$x(t) = \sum\limits_{l = 1}^n {{{\rm{imf}}_l}(t)} + {\rm{res}}$$ (1) 式中，x(t)是原始信号；
${\rm{imf}}{_l}(t)$ 是进行EMD时第l次筛选出的IMF，它代表了原始信号从高到低各个频率段的成分，不同信号得到IMF的阶数可能会有差异，这充分地体现了EMD对信号的自适应性；n是得到的IMF的数量；res是最后的残余分量。2.2 条件经验模式分解方法及流程
2.2.1 IMF筛选条件
为了克服传统的EMD凭借经验选取前几阶IMF重构脑电信号时会导致某些脑电信号的样本中混入多余信息或漏掉某些有用信息的问题，本文根据EEG信号的特点，采用各阶IMF和原始信号的相关性系数[17]作为第1个筛选条件，并提出基于相对能量占有率的第2个筛选条件。
(1) 基于相关性系数的筛选。相关性定义为
$$ r = \frac{{\displaystyle\sum\limits_{i = 1}^N {({{\rm{imf}}_i} - {\overline{\rm{imf}}})({x_i} - \mathop x\limits^\_ )} }}{\sqrt {{\displaystyle\sum\limits_{i = 1}^N {{{({{\rm{imf}}_i} - {\overline{\rm{imf}}} )}^2}{\displaystyle\sum\limits_{i = 1}^N {{{({x_i} - \mathop x\limits^\_ )}^2}} } } }}} $$ (2) 式中，r表示一个IMF与原始信号的相关性系数，
${\overline{\rm{imf}}} = \dfrac{1}{n}\displaystyle\sum\nolimits_{i = 1}^N {{{\rm{imf}}_i}} $ , x表示原始信号，$\mathop x\limits^\_ = \dfrac{1}{n}\displaystyle\sum\nolimits_{i = 1}^N {{x_i}} $ , N表示信号的采样频率。计算每个IMF和原始信号的相关性系数，由于相关性系数越大，表示该IMF中包含的原始信号的信息越多，满足相关性的筛选条件为$$ \left| r \right| \ge \alpha $$ (3) 式中，
$\alpha $ 是设定的筛选阈值且$0 \le \alpha \le 1$ 。(2) 基于相对能量占有率的筛选。IMF的能量函数为
$${E_l} = \sum\limits_{i = 1}^N {{{\rm{imf}}_l}{{(i)}^2}} $$ (4) 式中，
${E_l}$ 表示第$l$ 个IMF的能量，N表示信号的采样频率。接着可以求出各个IMF的能量分别为${E_1}, $ ${E_2}, ··· ,{E_n}$ 。定义IMF的相对能量占有率为
$$ q = \frac{{{E_l}}}{{{E_1} + {E_2} + ··· + {E_n}}} $$ (5) 式中，
$q$ 是第$l$ 个IMF的相对能量占有率，相对能量占有率越高，表示该IMF的波动越明显，有效成分越多。计算每个IMF的相对能量占有率，满足相对能量占有率的筛选条件定义为$$ q \ge \beta $$ (6) 式中，
$\beta $ 是设定的筛选阈值且$0 \le \beta \le 1$ 。对满足筛选条件的IMF进行信号的重构，即
$$ y = \sum\limits_{i = 1}^n {{{\rm{imf}}_i}} $$ (7) 式中，y代表重构的信号，i表示满足筛选条件的IMF的数量。
2.2.2 条件经验模式分解算法流程
本文的条件经验模式分解算法流程如下：
步骤 1 对一个通道的脑电信号进行EMD分解过程，得到该通道的各阶IMF和剩余分量；
步骤 2 去除掉残余分量；
步骤 3 根据前期的研究发现，与想象左右手运动的脑电信号相关的信息主要包含在前5阶的IMF中，所以只保留前5阶的IMF进行分析；
步骤 4 基于相关性系数的IMF筛选，根据式(2)计算该通道中各阶IMF与进行EMD过程前的脑电信号的相关性，然后根据式(3)筛选IMF；
步骤 5 基于相对能量占有率的IMF筛选，对通过相关性系数筛选后的IMF，根据式(4)计算得到该通道中各阶IMF的能量，然后根据式(5)计算该通道中各阶IMF的相对能量占有率，最后根据式(6)筛选IMF；
步骤 6 利用筛选出的有效IMF重构脑电信号；
步骤 7 对脑电信号的其余通道数据分别进行前6步的步骤；
步骤 8 得到经过处理后的脑电信号数据。
3. 串并行卷积神经网络
3.1 卷积神经网络
卷积神经网络[18,19]是一种能够直接输入原始空间的特征，并在网络内部自动的学习得到进一步优化的特征表示，从而更加有利于对原始的样本进行分类的算法。目前，卷积神经网络已经在分类识别领域发挥着十分重要的作用。相比于全连接网络，权值共享、局部感受野和降采样是卷积神经网络的3个特征，这3个特征可以极大地减少连接权值的数量，从而减少模型的复杂度，加快模型训练速度。
卷积操作是卷积神经网络中最重要的部分，其主要作用是对输入的数据进行特征提取，卷积的计算为
$$ s_j^d = f \left(\sum\limits_{i \in {M_j}} {s_i^{d - 1}*w_{ij}^d + b_i^d} \right) $$ (8) 式中，
$s_j^d$ 表示第d个卷积层中的第j个特征图，$w_{ij}^d$ 为第d层的第j个特征与第d–1层的第i个特征的连接权值，*表示卷积运算，${M_j}$ 是输入特征的集合，b为偏置值，$f( \cdot )$ 为激活函数。池化操作也就是对卷积操作得到的特征进行降采样，从而减少网络训练的参数量。目前主要使用的池化方法有：最大池化和平均池化。
3.2 串并行卷积神经网络
对多通道脑电信号进行特征提取时，为了同时提取出每个通道内部的特征和各个通道之间的特征，本文提出了并列使用双卷积核的SPCNN，其模型如图1所示，主要的5部分结构为：
(1) 输入层：输入数据是经过CEMD过程后的脑电数据；
(2) 卷积层1：采用了两种大小的卷积核(即：1×10和3×3)分别对输入数据进行卷积操作，多通道脑电信号有时间和通道两个尺度，其中1×10卷积核只在时间尺度上进行卷积，这样可以在不破坏每个通道内的脑电信号的情况下，提取出每个通道内部特征；3×3卷积核则在时间和通道同时进行卷积，可提取到各个通道之间的相关性特征，该层卷积核个数都为16个，卷积步长在各方向都为1，激活函数是线性修正单元(ReLu), padding参数为SAME；最大池化层1采用1×2的最大池化；拼接层1则把两个卷积通道得到的特征图按照对应行拼接；
(3) 卷积层2：也采用两种大小的卷积核(即：1×5和3×3)分别对拼接层1输出结果进行卷积，该层卷积核的个数为32个，卷积步长在各方向都为1，激活函数也是ReLu, padding参数为SAME；最大池化层2是1×4的最大池化；拼接层2同拼接层1把两个卷积通道得到的特征图按照对应行拼接；
(4) 两个全连接层：全连接层1神经元个数为300个，由于本文是对左右手运动想象脑电信号的二分类任务，所以全连接层2神经元个数设为2个，并且在两个全连接层中间加入了Dropout操作，以防止网络的过拟合；
(5) 输出层：输出通过网络后得到的特征向量，并把该特征输入Softmax分类器进行分类。
4. 线下实验
4.1 Emotiv脑电数据集分类实验
4.1.1 脑电数据采集实验
本文所使用的脑电数据采集仪是Emotiv，如图2所示，其采样频率为128 Hz。电极是按照国际10–20标准电极安放法安放，其中“CMS”和“DRL”是参考电极，如图3所示。
本文所用脑电信号为左右手运动想象脑电信号，脑电信号采集实验在一个比较安静的环境中进行，受试者为5名身体健康的研究生(年龄在22～24岁)，分别采集左右手运动想象脑电信号。单次采集实验过程如图4所示。
采集脑电信号具体步骤为：首先，让受试者平静并保持放松状态40 s，然后进入采集过程，先放松6 s，第6 s时会有提示音提示受试者开始想象左手或者右手运动，第10 s时会有提示音提示受试者停止想象。以1 s作为1组脑电信号样本数据，即采集1次可以得到4组脑电信号样本数据。接着重复以上采集过程，直到采集的左手和右手运动想象脑电信号都有600组为止，即一共有1200组脑电信号样本数据。
为了降低计算的数据量，本文只选择了位于运动感觉区域的F3,F4,FC5,FC6,T7,T8通道的信号进行分析，并把数据集按照4:1的比例分为了训练集和测试集。
4.1.2 数据预处理过程
由于采集的脑电信号中一般包含了眼电、肌电、工频杂波等背景噪声，为了降低脑电信号的背景噪声，并提高信噪比，本文对脑电数据进行了以下预处理过程：(1)去均值；(2) 8～30 Hz带通滤波，在想象左右手运动的过程中，主要是脑电信号的mu节律(8～13 Hz)和beta节律(14～30 Hz)发生变化，因此对脑电信号进行8～30 Hz带通滤波；(3)归一化，对原始的数据进行归一化处理，使得脑电数据的样本的值在[0, 1]之间。
4.1.3 确定筛选条件阈值
在CEMD算法中，相关性系数筛选条件和相对能量占有率筛选条件中阈值由以下两个实验得出。
(1)相关性系数筛选条件中阈值
$\alpha $ 的确定，取第1个人的脑电数据做实验，只使用相关性系数筛选条件筛选各阶IMF，令$\alpha $ 在0～1之间以0.05的间隔均匀取值，把得到处理后的样本输入到SPCNN中，得到的结果表明，当$\alpha $ 的值超过0.2时，脑电信号的识别准确率下降较快，图5为$\alpha $ 的值分别为0, 0.05, 0.10, 0.15和0.20时的识别准确率。从图5中可以看出，在阈值
$\alpha $ 为0.10和0.15的时候，准确率相对较高，所以本文设定$\alpha $ 的大小为0.10。(2)相对能量占有率筛选条件中阈值
$\beta $ 的确定，在相关性系数筛选条件的基础上，先设式(3)中的$\alpha $ 为0.1，使用相关性系数条件筛选IMF，再使用相对能量占有率筛选IMF，令$\beta $ 在0～1.00之间以0.05的间隔均匀取值，把得到处理后的样本输入到SPCNN中，得到的结果表明，当$\beta $ 的值超过0.15时，脑电信号的识别准确率下降较快，图6为$\beta $ 的值分别为0, 0.05, 0.10, 0.15和0.20时的识别准确率。从图6中可以看出，阈值
$\beta $ 为0.10时能够取到相对较高的值，所以本文设定$\beta $ 的值为0.10。4.1.4 实验结果与分析
为了验证CEMD算法的有效性，本文利用Emotiv采集的左右手运动想象脑电信号数据集进行了2个实验，第1个实验是直接采用了EMD算法得到的前3阶IMF重构脑电信号，第2个实验是采用CEMD算法得到的IMF重构脑电信号，把两种方法得到的重构脑电信号分别输入到SPCNN中分类，图7显示了两种方法的识别准确率。
从图7可以看出，5名受试者的识别准确率都是采用CEMD算法更高，由此说明本文提出的CEMD算法是有效的。
为了进一步说明本文提出的结合CEMD和SPCNN的脑电信号识别方法(CEMD-SPCNN)的良好性能，将其识别准确率与DBN[14], CNN, STFT-CNN[13], SPCNN以及两种经典的脑电信号特征提取算法CSP[8]、自适应共同空间模式(ACSP)[20]进行了对比。本文在对比实验中，CSP和ACSP都是采用的前2个特征值对应的特征向量作为空间滤波器，使用RBF核SVM作为分类器，得到准确率的结果如表1所示。
表 1 不同算法对5受试者脑电信号的识别准确率(%)算法 CSP ACSP DBN CNN STFT-CNN SPCNN 本文CEMD-SPCNN S01 65.00 77.50 87.08 86.25 88.75 90.42 93.33 S02 81.67 82.92 87.50 87.92 89.17 91.25 94.17 S03 98.33 97.08 95.83 95.83 96.67 97.08 99.16 S04 76.25 78.33 83.33 85.42 85.42 86.25 89.58 S05 95.42 96.25 93.75 91.67 92.50 94.17 96.67 均值 83.33 86.41 89.50 89.42 90.50 91.83 94.58 方差 190.01 91.88 26.51 18.61 18.18 16.62 13.02 从表1可以看出，对比CNN, STFT-CNN和SPCNN 3种方法的结果，SPCNN的识别准确率更高，表明SPCNN能够更充分地利用脑电信号中的有效信息，本文结合CEMD和SPCNN的方法CEMD-SPCNN在5位受试者的数据的识别准确率都高于其它方法，本文方法比其它几种方法的方差更小，表明本文所提出的方法具有更好的稳定性。
4.2 公开数据集BCI competition IV 2b识别实验
本文采用了第4届BCI竞赛的公开数据集BCI competition IV 2b对作进一步验证。该数据集一共包含了9位受试者的左右手运动想象脑电数据，每位受试者分别采集了5次，前2次采集每次包含了120组数据，并且是没有反馈的，后3次的采集每次包含了160组数据，并且包含了反馈，即：每位受试者一共采集了720组实验数据。采集过程中，主要是记录了C3, Cz和C4 3个通道的脑电信号，采样频率是250 Hz，对采集的信号进行了0.5～100 Hz的带通滤波以及50 Hz的陷波滤波。
对该数据集也同上一数据集进行相同处理，在该部分中，为了适应脑电数据的格式变化，对SPCNN中的部分参数进行了改动，即改为：卷积核1: 1×15、卷积核2: 3×6、卷积核3: 1×10、卷积核4: 3×3、池化层1: 1×5以及池化层2: 1×5。
为了验证结合CEMD和SPCNN脑电信号识别方法在公开数据集BCI competition IV 2b上的识别效果，将其识别准确率与BCI竞赛的前3名(记为：Chin, Gan和Coyle)结果[21], CSP[8], ACSP[20], DBN[14], CNN, STFT-CNN[13]以及SPCNN进行对比，对比结果如表2所示。
表 2 不同算法对BCI competition IV 2b数据集的识别准确率(%)算法 Chin Gan Coyle CSP ACSP DBN CNN STFT-CNN SPCNN 本文CEMD-SPCNN B01 70.00 71.00 60.00 66.56 67.50 66.56 72.22 75.00 76.39 80.56 B02 61.00 61.00 56.00 57.81 55.31 62.50 61.03 61.76 63.24 64.71 B03 61.00 57.00 56.00 61.25 62.19 60.00 61.11 62.50 62.50 64.58 B04 98.00 97.00 89.00 94.06 94.69 96.87 98.65 98.65 99.32 99.32 B05 93.00 86.00 79.00 80.63 76.88 82.19 86.48 87.16 87.84 88.51 B06 81.00 81.00 75.00 75.00 75.94 77.50 79.17 80.56 81.25 83.33 B07 78.00 81.00 69.00 72.50 71.25 76.56 78.47 77.08 79.17 81.25 B08 93.00 92.00 93.00 89.38 89.38 88.75 86.18 86.18 86.84 90.13 B09 87.00 89.00 73.00 85.63 81.25 85.94 81.25 82.64 84.03 86.81 均值 80.22 79.44 72.22 75.86 74.93 77.43 78.28 79.06 80.06 82.13 方差 192.19 190.03 181.69 158.75 157.50 155.85 147.92 138.63 137.52 129.78 从表2中可以看出，本文提出的结合CEMD和SPCNN方法CEMD-SPCNN在公开数据集BCI competition IV 2b中大部分对象的数据有着更好的结果。由于脑电信号具有个体差异性，所以极个别对象的数据的识别准确率未能取到最高。但与其它几种方法相比，本文方法的平均识别准确率最高、方差最小，由此说明了本文方法的有效性。
5. 线上实验
为了验证本文算法的有效性，在设计的智能轮椅的平台上进行了在线实验。智能轮椅系统主要包含了脑电信号采集、信号处理、无线通信模块、控制系统以及智能轮椅5个部分，智能轮椅系统总体结构如图8所示。
Emotiv脑电采集帽可同时采集肌电信号和脑电信号，通过前期的实验观察，当戴上Emotiv脑电帽时，咬牙可使F8通道有着明显电压变化，使用该信号来控制轮椅开始实验和停止实验；眨眼可使FC4通道有着较为明显的电压变化，使用该信号控制轮椅直行前进；左手运动想象脑电信号和右手运动想象脑电信号分别用来控制轮椅进行左转和右转，通过采集F3, F4, FC5, FC6, T7和T8通道的脑电信号，并对其使用本文提出的结合CEMD和SPCNN的识别方法对其进行分类。
第1个数据集中前3个人分别进行了控制智能轮椅直行、左转以及右转的在线实验，各类转向实验交叉进行，直到各类实验分别进行了50次，得到的在线识别准确率如表3所示。
表 3 各类操作在线识别准确率(%)操作 直行 左转 右转 S01 96 84 86 S02 94 90 82 S03 98 88 92 从表3中可以看出，肌电信号的在线识别率比脑电信号的在线识别率高，这是因为肌电信号比脑电信号有着更加明显的特征，更加容易识别。对比表1和表3中的识别准确率可以发现，整体上脑电数据的离线识别率要比在线识别率高，这是由于进行在线实验时需要考虑的各种因素(如：周围环境的影响以及实验时间较长时，受试者容易疲劳等)较多造成的。总体上看，本文设计的智能轮椅系统能够较好地完成前进、左转和右转功能，验证了本文算法的有效性。
6. 结束语
本文提出一种结合CEMD和SPCNN的运动想象脑电信号识别算法CEMD-SPCNN，在对脑电信号进行EMD处理的过程中，采用相关性系数和相对能量占有率来对IMF进行筛选，提高了选取的IMF的有效性。根据脑电信号的多通道特性，对CNN进行了结构上的改进，提出SPCNN网络模型。在多个运动想象脑电信号数据集上进行实验，得到的实验结果表明，本文算法比CSP, ACSP, DBN以及CNN等算法的识别准确率更高。最后，在自行设计的智能轮椅平台上进行的在线实验也进一步验证了本文算法的有效性。
-
表 1 不同算法对5受试者脑电信号的识别准确率(%)
算法 CSP ACSP DBN CNN STFT-CNN SPCNN 本文CEMD-SPCNN S01 65.00 77.50 87.08 86.25 88.75 90.42 93.33 S02 81.67 82.92 87.50 87.92 89.17 91.25 94.17 S03 98.33 97.08 95.83 95.83 96.67 97.08 99.16 S04 76.25 78.33 83.33 85.42 85.42 86.25 89.58 S05 95.42 96.25 93.75 91.67 92.50 94.17 96.67 均值 83.33 86.41 89.50 89.42 90.50 91.83 94.58 方差 190.01 91.88 26.51 18.61 18.18 16.62 13.02 
下载: 导出CSV
表 2 不同算法对BCI competition IV 2b数据集的识别准确率(%)
算法 Chin Gan Coyle CSP ACSP DBN CNN STFT-CNN SPCNN 本文CEMD-SPCNN B01 70.00 71.00 60.00 66.56 67.50 66.56 72.22 75.00 76.39 80.56 B02 61.00 61.00 56.00 57.81 55.31 62.50 61.03 61.76 63.24 64.71 B03 61.00 57.00 56.00 61.25 62.19 60.00 61.11 62.50 62.50 64.58 B04 98.00 97.00 89.00 94.06 94.69 96.87 98.65 98.65 99.32 99.32 B05 93.00 86.00 79.00 80.63 76.88 82.19 86.48 87.16 87.84 88.51 B06 81.00 81.00 75.00 75.00 75.94 77.50 79.17 80.56 81.25 83.33 B07 78.00 81.00 69.00 72.50 71.25 76.56 78.47 77.08 79.17 81.25 B08 93.00 92.00 93.00 89.38 89.38 88.75 86.18 86.18 86.84 90.13 B09 87.00 89.00 73.00 85.63 81.25 85.94 81.25 82.64 84.03 86.81 均值 80.22 79.44 72.22 75.86 74.93 77.43 78.28 79.06 80.06 82.13 方差 192.19 190.03 181.69 158.75 157.50 155.85 147.92 138.63 137.52 129.78
下载: 导出CSV
-
RAMADAN R A and VASILAKOS A V. Brain computer interface: Control signals review[J]. Neurocomputing, 2017, 223: 26–44. doi: 10.1016/j.neucom.2016.10.024 佘青山, 陈希豪, 高发荣, 等. 基于感兴趣脑区LASSO-Granger因果关系的脑电特征提取算法[J]. 电子与信息学报, 2016, 38(5): 1266–1270. doi: 10.11999/JEIT150851SHE Qingshan, CHEN Xihao, GAO Farong, et al. Feature extraction of electroencephalography based on LASSO-Granger causality between brain region of interest[J]. Journal of Electronics &Information Technology, 2016, 38(5): 1266–1270. doi: 10.11999/JEIT150851 YU Tianyou, XIAO Jun, WANG Fangyi, et al. Enhanced motor imagery training using a hybrid BCI with feedback[J]. IEEE Transactions on Biomedical Engineering, 2015, 62(7): 1706–1717. doi: 10.1109/TBME.2015.2402283 KAUFMANN T, HERWEG A, and KÜBLER A. Toward brain-computer interface based wheelchair control utilizing tactually-evoked event-related potentials[J]. Journal of NeuroEngineering and Rehabilitation, 2014, 11: No.7. doi: 10.1186/1743-0003-11-7 WANG Haofei, DONG Xujiong, CHEN Zhaokang, et al. Hybrid gaze/EEG brain computer interface for robot arm control on a pick and place task[C]. The 37th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Milan, Italy, 2015: 1476–1479. doi: 10.1109/EMBC.2015.7318649. 陈强, 陈勋, 余凤琼. 基于独立向量分析的脑电信号中肌电伪迹的去除方法[J]. 电子与信息学报, 2016, 38(11): 2840–2847. doi: 10.11999/JEIT160209CHEN Qiang, CHEN Xun, and YU Fengqiong. Removal of muscle artifact from EEG data based on independent vector analysis[J]. Journal of Electronics &Information Technology, 2016, 38(11): 2840–2847. doi: 10.11999/JEIT160209 HSU W Y. EEG-based motor imagery classification using neuro-fuzzy prediction and wavelet fractal features[J]. Journal of Neuroscience Methods, 2010, 189(2): 295–302. doi: 10.1016/j.jneumeth.2010.03.030 WU Shanglin, WU Chunwei, PAL N R, et al. Common spatial pattern and linear discriminant analysis for motor imagery classification[C]. 2013 IEEE Symposium on Computational Intelligence, Cognitive Algorithms, Mind, and Brain, Singapore, 2013: 146–151. doi: 10.1109/CCMB.2013.6609178. ZHANG Yu, WANG Yu, ZHOU Guoxu, et al. Multi-kernel extreme learning machine for EEG classification in brain-computer interfaces[J]. Expert Systems with Applications, 2018, 96: 302–310. doi: 10.1016/j.eswa.2017.12.015 KEVRIC J and SUBASI A. Comparison of signal decomposition methods in classification of EEG signals for motor-imagery BCI system[J]. Biomedical Signal Processing and Control, 2017, 31: 398–406. doi: 10.1016/j.bspc.2016.09.007 PARK C, LOONEY D, REHMAN N U, et al. Classification of motor imagery BCI using multivariate empirical mode decomposition[J]. IEEE Transactions on Neural Systems and Rehabilitation Engineering, 2013, 21(1): 10–22. doi: 10.1109/TNSRE.2012.2229296 DOSE H, MØLLER J S, IVERSEN H K, et al. An end-to-end deep learning approach to MI-EEG signal classification for BCIs[J]. Expert Systems with Applications, 2018, 114: 532–542. doi: 10.1016/j.eswa.2018.08.031 ZHANG Jin, YAN Chungang, and GONG Xiaoliang. Deep convolutional neural network for decoding motor imagery based brain computer interface[C]. 2017 IEEE International Conference on Signal Processing, Communications and Computing, Xiamen, China, 2017: 1–5. doi: 10.1109/ICSPCC.2017.8242581. AN Xiu, KUANG Deping, GUO Xiaojiao, et al. A deep learning method for classification of EEG data based on motor imagery[C]. The 10th International Conference on Intelligent Computing, Taiyuan, China, 2014: 203–210. doi: 10.1007/978-3-319-09330-7_25. LI Shufang, ZHOU Weidong, YUAN Qi, et al. Feature extraction and recognition of ictal EEG using EMD and SVM[J]. Computers in Biology and Medicine, 2013, 43(7): 807–816. doi: 10.1016/j.compbiomed.2013.04.002 TARAN S, BAJAJ V, SHARMA D, et al. Features based on analytic IMF for classifying motor imagery EEG signals in BCI applications[J]. Measurement, 2018, 116: 68–76. doi: 10.1016/j.measurement.2017.10.067 MU Yashuang, LIU Xiaodong, and WANG Lidong. A Pearson’s correlation coefficient based decision tree and its parallel implementation[J]. Information Sciences, 2018, 435: 40–58. doi: 10.1016/j.ins.2017.12.059 LECUN Y, BOTTOU L, BENGIO Y, et al. Gradient-based learning applied to document recognition[J]. Proceedings of the IEEE, 1998, 86(11): 2278–2324. doi: 10.1109/5.726791 SAKHAVI S, GUAN Cuntai, and YAN Shuicheng. Learning temporal information for brain-computer interface using convolutional neural networks[J]. IEEE Transactions on Neural Networks and Learning Systems, 2018, 29(11): 5619–5629. doi: 10.1109/TNNLS.2018.2789927 SUN Shiliang and ZHOU Jin. A review of adaptive feature extraction and classification methods for EEG-based brain-computer interfaces[C]. 2014 International Joint Conference on Neural Networks, Beijing, China, 2014: 1746–1753. doi: 10.1109/IJCNN.2014.6889525. LU Na, LI Tengfei, REN Xiaodong, et al. A deep learning scheme for motor imagery classification based on restricted Boltzmann machines[J]. IEEE Transactions on Neural Systems and Rehabilitation Engineering, 2017, 25(6): 566–576. doi: 10.1109/TNSRE.2016.2601240 期刊类型引用(6)
1. 费克玲，蔡霄仙，陈顺芝，潘礼正，王炜. 基于闪噪谱方法及加权滤波器组共空间模式的运动想象脑电信号识别. 生物医学工程学杂志. 2023(06): 1126-1134 . 
百度学术2. 周成诚，曾庆军，杨康，胡家铭，韩春伟. 基于高效通道注意力模块的运动想象脑电识别. 计算机与现代化. 2023(12): 19-23 . 百度学术3. 罗志增，鲁先举，周莹. 基于脑功能网络和样本熵的脑电信号特征提取. 电子与信息学报. 2021(02): 412-418 . 
本站查看4. 王增尉，刘佳奇，戴露，李芷萱，王启月，李蛟，赵宏伟. 基于脑机接口的智能家居控制系统. 吉林大学学报(信息科学版). 2021(01): 121-126 . 百度学术5. 谷学静，位占锋，刘海望，郭俊，沈攀. 共空间模式结合卷积神经网络的脑电信号分类. 激光杂志. 2021(04): 100-104 . 百度学术6. 谷学静，位占锋，刘海望，郭俊，沈攀. 基于小波包和串并行CNN的脑电信号分类. 微电子学与计算机. 2021(06): 60-65 . 百度学术其他类型引用(8)
-
下载:
百度学术
计量
- 文章访问数: 2587
- HTML全文浏览量: 1429
- PDF下载量: 119
- 被引次数: 14
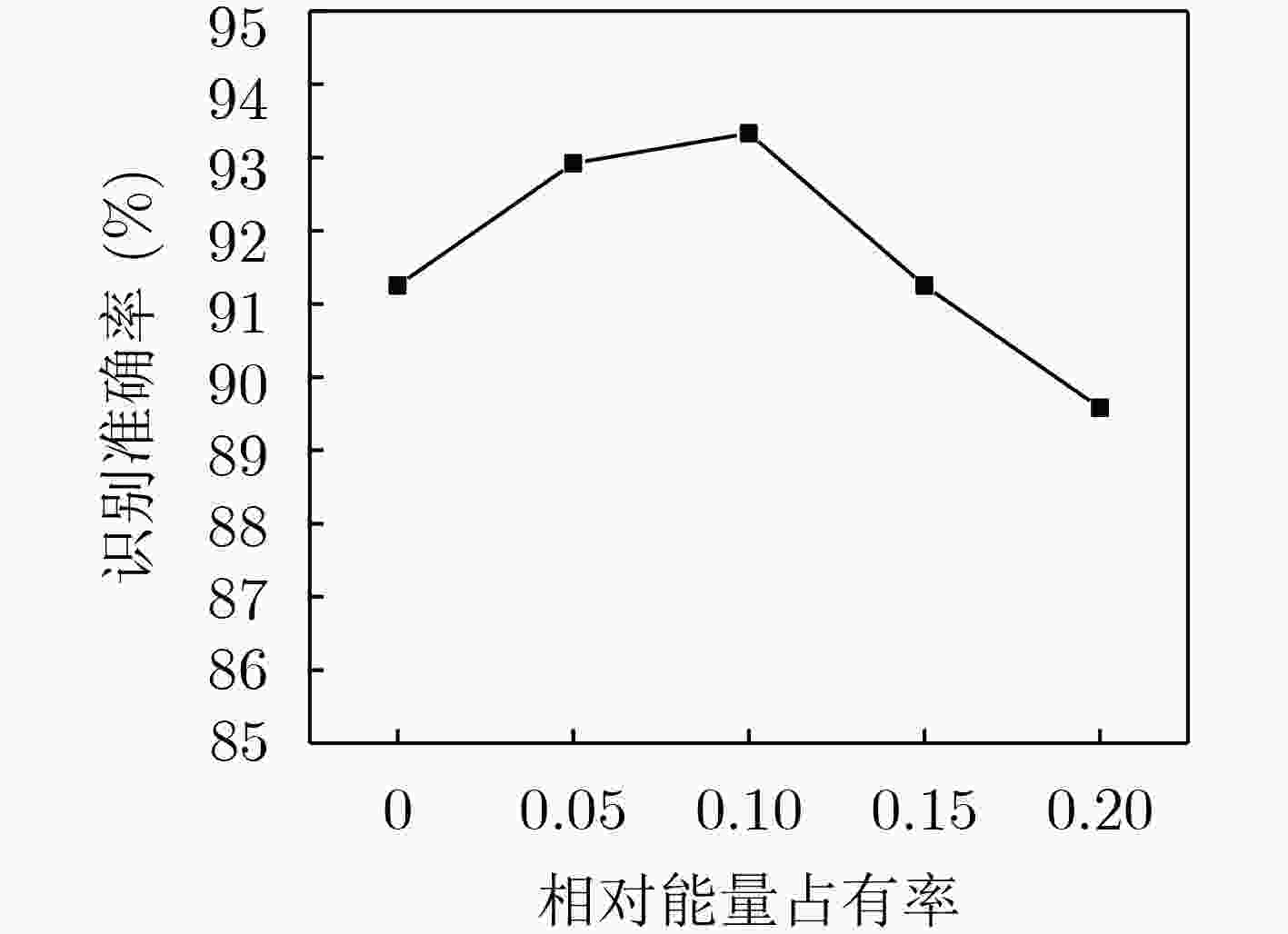
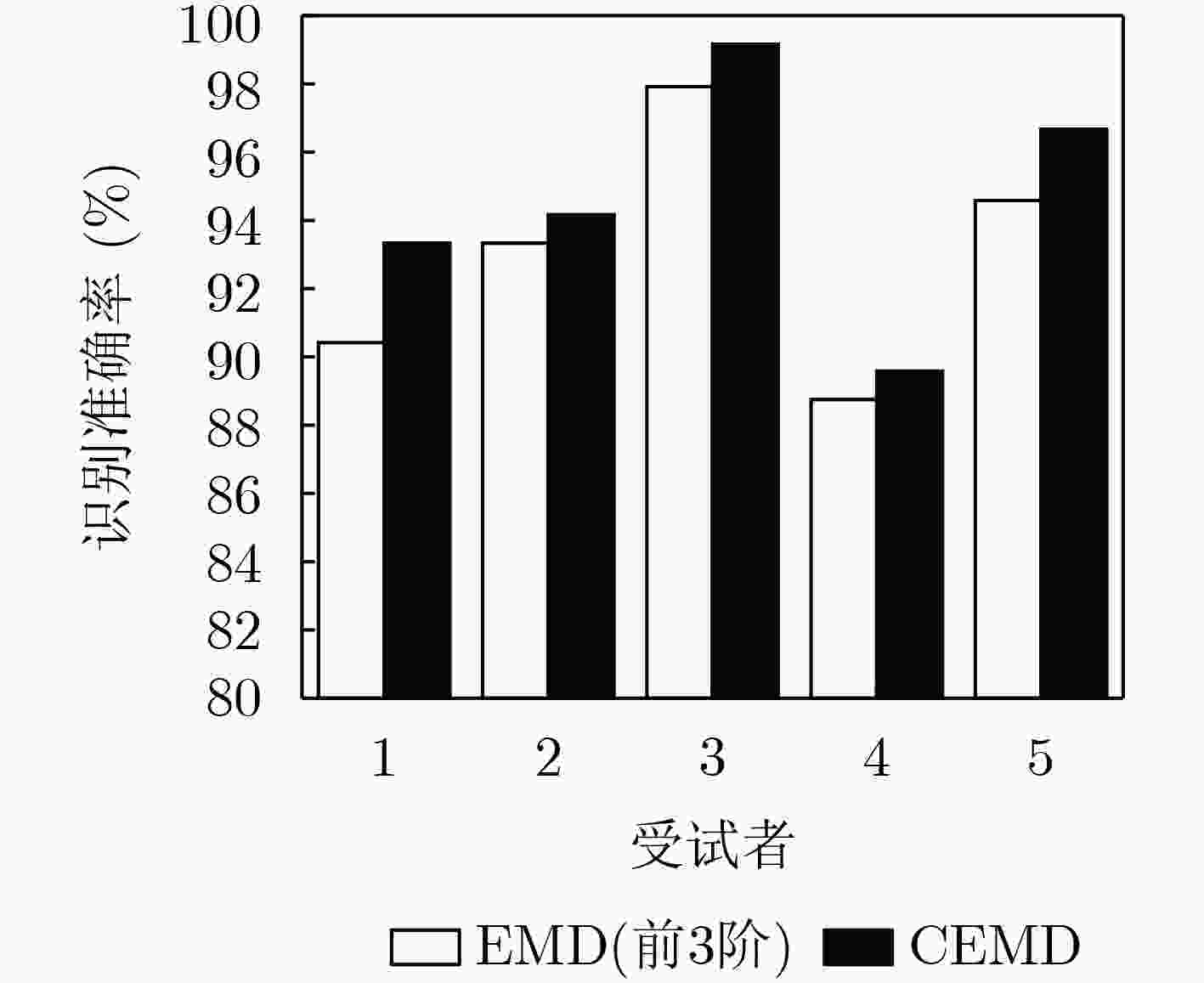
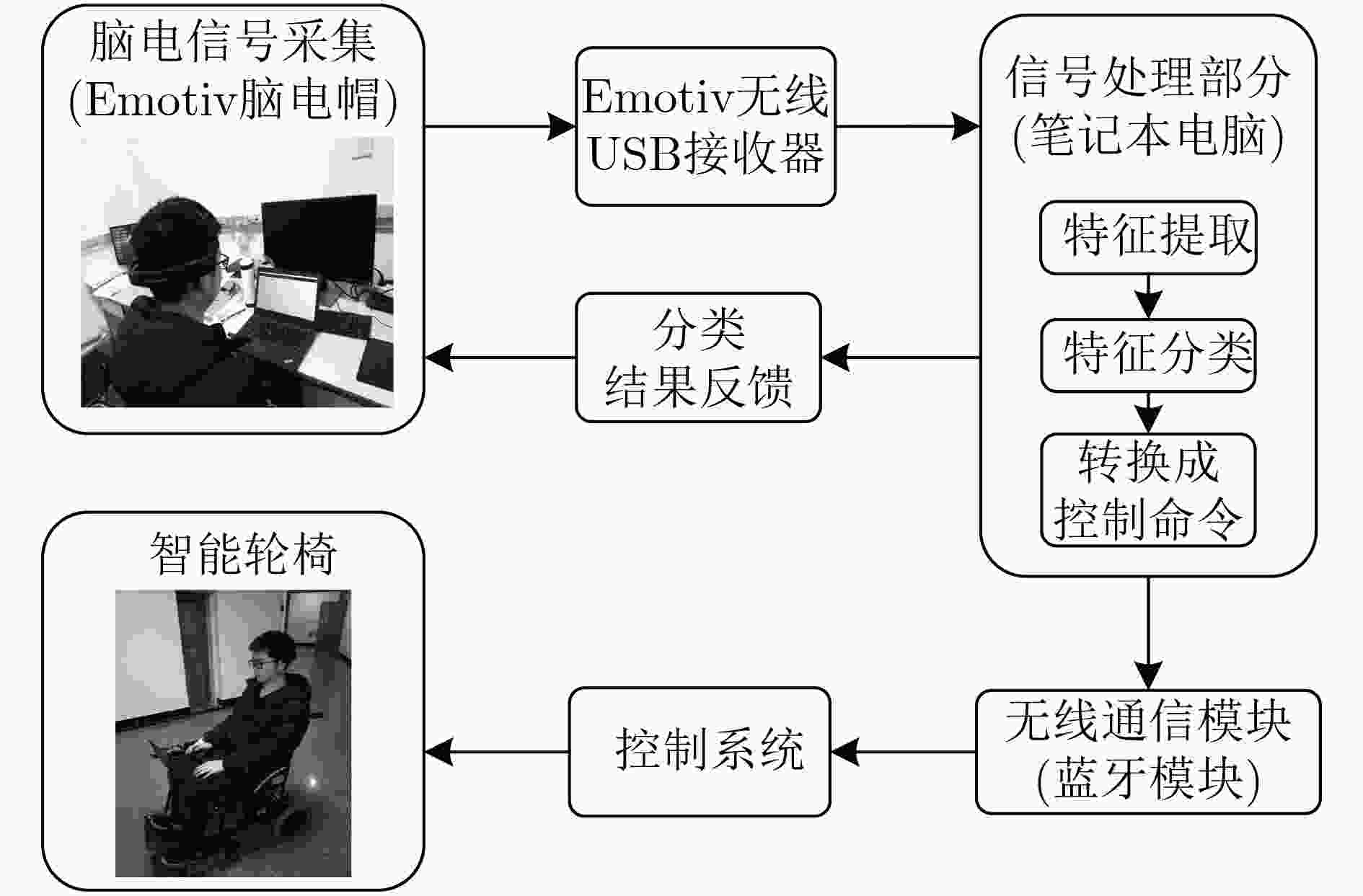
下载:
